Authentication in the Taos Operating System
Edward Wobber, Martin Abadi, Mike Burrows, and Butler Lampson
This
web page was made from a Word original. There may be problems with the formatting.
To see the intended appearance follow one of these links: Postscript of SRC report, Acrobat of SRC report, Acrobat of TOCS version, Word, Acrobat
of Word version
This
paper appeared in ACM Transactions on
Computer Systems, 12,1, February
1994. An earlier version appeared in the Proceedings
of the 14th ACM Symposium on Operating System Principles, December 1993.
This
version was reconstructed from the printed version by OCR and hand editing.
Authors’ Abstract
We describe a design for security in a distributed system and its implementation. In our design, applications gain access to security services through a narrow interface. This interface provides a notion of identity that includes simple principals, groups, roles, and delegations. A new operating system component manages principals, credentials, and secure channels. It checks credentials according to the formal rules of a logic of authentication. Our implementation is efficient enough to support a substantial user community.
1 Introduction
We describe a design for security in a distributed system and a particular implementation of this design. We present both the external interface and the major internal interfaces of our implementation. A formal logic [Abadi et al. 1993b; Lampson et al. 1992] guided our design. We explain the correspondence between implementation and logic, in particular how an authentication credential represents a formula and how an authentication is a proof. We discuss our experience and some performance results; the implementation is efficient enough to support a substantial user community.
For our purposes, a distributed system is a collection of nodes connected by an insecure network; each node is a computer running an operating system that is trusted for local security. The setting for our implementation is a distributed system where each node is a Firefly shared-memory multiprocessor running the Taos operating system [Thacker et al. 1988]. Taos is completely multithreaded, yet also implements a protected address-space model close enough to that of Unix that it can run most Unix binaries. Remote procedure call is the primary means of interprocess communication. Although Taos has been a convenient test vehicle, our only real dependence on it was that we could adapt it to our needs.
We use the access control model of security [Lampson 1974] extended with compound principals [Gasser et al. 1989]. In this model there are objects (files, printers, etc.), requests, and principals (users, machines, etc.) that utter requests. Each object has a guard or reference monitor that examines each request and decides whether or not to grant it. The request must first be authenticated to identify the principal that uttered it, and then authorized only if the principal has the right to perform the requested operation on the object. The pieces of evidence that identify the uttering principal are called credentials. Compound principals provide a precise and uniform representation for the sources of requests in a distributed system, including users, machines, channels, programs, delegations, roles, and groups.
In each node, a new operating system component called the authentication agent manages compound principals and their credentials. Applications access security services through a narrow interface to the local agent. The agent implements all credential exchanges and validations, communicating with agents in other nodes when necessary and checking credentials according to the formal rules of the logic. The agent uses a distributed certification database for names, group memberships, and executable images. From the underlying operating system it needs only a bidirectional secure channel to each application, and global names for the channels between the application and the outside world.
Many systems that offer distributed security do so entirely at the level of the application, either to avoid changing the kernel or because most operating systems do not support a coherent model of user identity throughout the network. Our basic design can be implemented in the same way, with the authentication agent linked into each application as a library.
In fact, however, our distributed security is part of the operating system. This has one major advantage: the notion of identity or principal is built in at a very low level and is represented consistently everywhere. There is no distinction between local and remote principals. Minor advantages are that it is easy to provide the necessary secure channels between the authentication agent and applications, and easy for a child process to inherit the authority of its parent. The trusted computing base does not get any bigger, because the operating system must be trusted anyway.
The next section reviews the logic. Section 3 presents the application programming interface (API) to Taos security. Section 4, the heart of the paper, describes the implementation in detail. Finally, Section 5 discusses our experience with the system in practice.
We do not address either denial of service or the kind of non-disclosure security policies that are based on an information flow model. We touch only briefly on the problems of compatibility with other security mechanisms, such as Kerberos [Steiner et al. 1988] and OSF DCE Security [Open Software Foundation 1992].
2 Background
In this section we explain our treatment of encryption and time, sketch the rules of our authentication logic, and give an extended example of its use. Other papers treat these matters in detail [Abadi et al. 1993b; Lampson et al. 1992].
We use shared key encryption to secure short-term node-to-node channels. All other encryption is public key [Rivest et al. 1978] and is done only for integrity, not for secrecy. We write K and K-1 for the public and secret keys of a key pair. We say that a message encrypted with K-1 is signed by K so that we need to mention only the public key.
Our authentication system relies on signed statements called certificates. These form the building blocks of credentials, which are proofs of authenticity. We view certificates and credentials both as logical formulas and, in the implementation, as data.
Time does not appear explicitly in the logic; formally, assumptions and proofs concern only a given, implicit instant. In our system, on the other hand, a time interval qualifies each certificate. A certificate is valid only for the specified interval. Therefore, the conclusion of a proof is valid only for the intersection of the intervals of all the certificates used in the proof. Since these certificates typically originate at different nodes, it is important that nodes have loosely synchronized clocks. For synchronization we do not have a secure time server, but instead rely on the clocks of individual nodes.
However, we can easily tolerate a one-minute skew because certificates are valid for at least a few minutes. The most obvious effect of a large skew is that authentication becomes impossible because the validity interval of a formula is empty or does not include the current time. If a certificate originates at a node whose clock is much later than real time, or is used at a node whose clock is much earlier, it is also possible that the certificate will be mistakenly considered valid even though it has expired.
2.1 Some notations and rules
We write A says S to mean that principal A supports the statement S (an assertion or a request). We write A ̃ B when A speaks for B, meaning that if A makes a statement then B makes it too:[1]
if (A ̃ B) and (A says S)
then (B says S)
We think of A as being stronger than B. The ̃ relation is a partial order; that is, it is reflexive, antisymmetric, and transitive. It obeys many of the same laws as implication, so we use the same symbol for it. Principals include:
• Simple principals. Users, machines.
• Channels. Network addresses, encryption keys. If S appears on channel C then C says S. In particular, K says S represents a certificate containing S and signed by K. A channel is the only kind of principal that can directly make a statement, since a message can arrive only on a channel.
• Groups. Sets of principals. If A is a member of G then A ̃ G, so A says S implies G says S. A group can be thought of as the disjunction of its members.
• Principals in roles. We write A as R for A in role R (for example, Bob as Admin for Bob acting as an administrator). A principal can adopt a role in order to reduce its rights [Lampson et al. 1992, Section 6]. That is, A ̃ (A as R).
• Conjunctions of principals. We write A Ù B for the conjunction of A and B. If both A says S and B says S then (A Ù B) says S as well.
• Principals quoting principals. We write B | A for B quoting A. If B says A says S then (B | A) says S.
• Principals acting on behalf of others. We write B for A for B acting on behalf of A. The principal B for A is stronger than B | A, since (B for A) says S when B says A says S and in addition B is authorized to act as A’s delegate.
The handoff axiom represents the transfer of authority:
if A says (B ̃ A)
then (B ̃ A)
In other words, we believe that B speaks for A when A says so. Therefore, if A says (B ̃ A) and B says S then A says S. Similarly, we have a delegation axiom:
if A says ((B | A) ̃ (B for A))
then ((B | A) ̃ (B for A))
It means that we believe A when it says that B | A speaks for B for A, that is, that B can act as A’s delegate.[2] Therefore, if A says ((B | A) ̃ (B for A)) and B says A says S then (B for A) says S. Comparing the result (B for A) says S with that of a handoff, A says S, we note that it mentions B: both delegate and delegator lend some of their authority, and the identity of the delegate is not forgotten.
The operations as, Ù, |, and for are monotonic with respect to ̃: if B ̃ B' and A ̃ A' then
|
(B as A) |
̃ (B' as A') |
|
(B Ù A) |
̃ (B' Ù A') |
|
(B | A) |
̃ (B' | A') |
|
(B for A) |
̃ (B' for A') |
2.2 Logic and authentication
This section gives a simplified example of how logic can be used to reason about authenticating compound principals; there is more detail in later sections. In the example, a machine Vax4 is booted with an operating system OS. Together, Vax4 and OS form a node WS. A user Bob logs in to WS. We consider the reasoning necessary to authenticate requests from this login session to a file server FS.
In order to establish credentials, Vax4 must possess a secret. For example, if (Kvax4, K-1vax4) is a public key pair, then K-1vax4 is a suitable secret. Let K-1vax4 be available only to Vax4’s boot firmware, not to any of the operating systems it can run. At boot time, K-1vax4 is used to sign a boot certificate that transfers authority to a newly generated key Kws; in the logic, this certificate reads:
(Kvax4 as OS) says (Kws ̃ (Kvax4 as OS)) (1)
We call Kws the node key for WS. It speaks not for Kvax4 but for a weaker principal WS = (Kvax4 as OS), that is, Kvax4 in the role of the boot image. After booting, WS gets the boot certificate and K-1, but does not know K-1vax4.
We treat login as a specialized form of delegation. When Bob logs in, K-1bob is used to sign a delegation certificate that transfers authority to WS:
Kbob says ((Kws | Kbob) ̃ (Kws for Kbob)) (2)
Consider now a request from the login session to a file server FS. There must first exist a channel Cbob over which to issue requests. As observed by FS, a request appears as a statement RQ on this channel:
Cbob says RQ (3)
To back RQ, WS supplies (1) and (2), and writes a channel certificate:
(Kws | Kbob) says (Cbob ̃ (Kws for Kbob)) (4)
This represents a handoff from the node to the channel.
By applying the delegation axiom to the delegation certificate (2), FS can deduce
(Kws | Kbob) ̃ (Kws for Kbob)
so the channel certificate (4) implies
(Kws for Kbob) says (Cbob ̃ (Kws for Kbob)) (5)
Further, FS can deduce
Cbob ̃ (Kws for Kbob) by applying the handoff axiom to (5), so the request (3) yields
(Kws for Kbob) says RQ (6)
And FS can deduce
Kws ̃ (Kvax4 as OS)
by applying the handoff axiom to the boot certificate (1), so (6) yields
((Kvax4 as OS) for Kbob) says RQ (7)
by monotonicity.
We still must prove that Kvax4 and Kbob correspond to Vax4 and Bob. To do this we must trust some certification authority or CA. Trusting a CA with known key Kca means believing that Kca speaks for any principal; in particular, Kca ̃ Vax4 and Kca ̃ Bob. Thus, FS can use the certificates
Kca says (Kvax4 ̃ Vax4)
Kca says (Kbob ̃ Bob)
and the handoff axiom to obtain
Kvax4 ̃ Vax4
Kbob ̃ Bob
then (7) to conclude
((Vax4 as OS) for Bob) says RQ
by monotonicity. That is, FS knows that Vax4 running OS requests RQ on behalf of Bob. The access control algorithm given in [Lampson et al. 1992, Section 9] can now determine whether the request should be granted.
The remainder of the paper describes how this authentication logic is implemented in Taos.
3 An API for Authentication
The logic is rather complex to be presented directly through a programming interface. Instead, Taos defines a simple and consistent set of security services. They are based on an abstract datatype Prin that represents principals, and a subtype Auth that represents principals that processes can speak for.
Section 3.1 gives the interface for sending and receiving authenticated messages; that is, it explains how a process that can speak for a principal P can make another process believe P says S. Section 3.2 gives the interface for authenticating and authorizing requests. Section 3.3 gives the interface for managing Auths; that is, it explains how a process can change the set of principals that it can speak for.
For brevity, we omit exceptions from the signatures of procedures.
3.1 Authenticating messages
We begin with a simplified version of the interface for sending and receiving authenticated messages, and improve it later in this section:
PROCEDURE Send(dest:Address; p:Auth; m:Msg);
PROCEDURE Receive(): (Prin, Msg);
Send transmits the statement p says m to the process at address dest. Symmetrically, if Receive returns (p,m), some process that speaks for p has invoked Send(dest,p,m); in other words, the receiver can believe that p says m.
The interface has no notion of a principal that a process speaks for by default. Instead, the Auth argument to Send requires the process to specify explicitly the principal that is uttering each message. Often a process has only one Auth, and we could have added a “working authority” to the process state and a SetWorkingAuth procedure (by analogy with the working directory), and dropped the Auth argument to Send or made it optional. This is similar to what Unix does with the effective uid. Or, to accommodate multi-threaded programs, we could have made the working authority part of the thread state.
This simplified version of the interface is unsatisfactory because it ties authentication and communication together too closely. To separate them, we make explicit the relation between a channel c and the principal p that it speaks for.
We assume that secure channels are available. A channel is secure if every message received on it comes from the same process. We might also require messages on the channel to be secret, that is, received only by certain processes; this is a simple extension that we will not discuss further. An abstract datatype Chan represents secure channels.
To transmit an authenticated message, a process sends it on a secure channel, the receiver gets the channel c on which the message arrives, and a new operation GetPrin returns the p that the channel speaks for. In other words, c names the principal p.
For this to work, a given channel must speak for at most one principal, so we need a cheap way to make channels. Our method is to take a single channel c on which a process can send securely, and then to multiplex many subchannels onto c, one for each principal that the process speaks for. Sending and receiving is done on these subchannels.
Our second try at an interface is thus:
PROCEDURE GetChan(dest:Address): Chan;
PROCEDURE GetSubChan(c:Chan; p:Auth): SubChan;
PROCEDURE Send(dest:SubChan; m:Msg);
PROCEDURE Receive(): (SubChan, Msg);
PROCEDURE GetPrin(c:SubChan): Prin;
The sending process first calls GetChan to get a secure channel c to the process at dest and then calls GetSubChan(c, p) to get a subchannel that speaks for p. The receiver calls GetPrin to recover a Prin.
The actual Taos interface has a further refinement: a process can utter many statements, perhaps made by different principals, in a single message. For example, one call could pass an array of names of files to delete and a parallel array of principals that are authorized to do the deletions. To make this work, we must reveal the addressing mechanism for subchannels: it is an integer called an authentication identifier or AID. The sender calls GetAID to learn the AID for a principal and sends it as an ordinary data value in the message. The receiver pairs the channel on which the message arrives with this AID to recover the speaking principal. So the actual Taos interface is:
PROCEDURE GetChan(dest:Address): Chan;
PROCEDURE GetAID(p:Auth): AID;
PROCEDURE Send(dest:Chan; m:Msg);
PROCEDURE Receive(): (Chan, Msg);
PROCEDURE GetPrin(c:Chan; aid:AID): Prin;
In Taos, the messages exchanged in this way are normally the call and return messages of remote procedure calls. RPC marshals an Auth parameter p by sending the result of Get AID(p), and unmarshals aid from channel c as the result of GetPrin(c, aid). It also gets the channel from the RPC binding, and of course it encapsulates the Send and Receive calls. The result is that the RPC client can simply use Prins and Auths as arguments and results, and does not have to call any of the procedures in this interface. This works for both calls and returns, so mutual authentication is possible.
3.2 Basic authentication and authorization
The receiver of an authenticated message calls GetPrin to find the Prin p that represents the sender of the message. It can then use Authenticate to turn p into a string name.
PROCEDURE Authenticate(p:Prin): TEXT;
The result of Authenticate can represent a compound principal such as Bob as admin, or it can be a simple name. Simple names are convenient for existing applications; Section 4.5 describes the somewhat ad hoc rules Taos uses to reduce compound principals to simple names.
The purpose of authentication is to tell the authorization service the source of a request. We therefore introduce another abstract datatype ACL to represent access control lists, and the authorization operation Check to determine whether acl grants access to p.
PROCEDURE Check(acl:ACL; p:Prin): BOOL;
Check both hides the details of naming and allows a convenient and efficient cache of recent successful authorizations.
Taos also offers operations for constructing and examining ACLs, but they are beyond the scope of this paper.
3.3 Managing principals
A Taos process can obtain an Auth in five ways:
• by inheritance from a parent process,
• by presenting a login secret,
• by adopting a role,
• by delegating rights, or
• by claiming delegated rights.
All but the first of these produce a new and unique Auth. In particular, each user session on a machine is represented by a different Auth. The interface for managing Auths is:
PROCEDURE SelfQ: Auth;
PROCEDURE Inheritance(): ARRAY OF Auth;
PROCEDURE New(name, password: TEXT): Auth;
PROCEDURE AdoptRole(a:Auth; role:TEXT): Auth;
PROCEDURE Delegate(a:Auth; b:Prin): Auth;
PROCEDURE Claim(b:Auth; delegation:Prin):
Auth;
PROCEDURE Discard(a:Auth; all:BOOL);
Self returns a default Auth for the current process. The default is specified when the process is created. Inheritance returns all the Auths that the process inherits from its parent.
New is used to generate entirely new credentials. The parameters describe a user name and a user-specific secret sufficient to generate the credentials described in Section 4.3. The result is an Auth that represents node for name, where node is the local node. This result reflects the fact that the user cannot make a request without involving the machine and the operating system.
AdoptRole weakens an authority by applying a role. If a represents A, then the result of AdoptRole(a,role) represents A as role.
Roles are used in two ways in Taos. First, a process can restrict its rights to those necessary to fulfill a particular function by calling AdoptRole on one of its existing Auths. Second, a Taos node can give some of its rights to a trusted process. Taos uses secure loading to determine whether an executable image is certified (see Section 4.4). After loading a certified image, Taos calls AdoptRole to create an Auth weaker than its own, which it hands off to the new process (for example, AdoptRole(Self(), “telnet-server”) for a login daemon). This mechanism bears some resemblance to Unix setuid execution. However, in Taos there is a stronger guarantee about the loaded program, and the program need not receive all the rights of the node. Further, the resulting rights, like those of the node, can be exercised over the network.
|
|
|
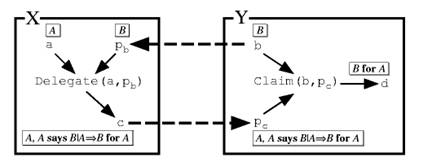
Figure 1: An example of delegation |
There is a natural role associated with many groups, for example the role of administrator with the group of administrators. Hence we use group names as roles, and adopt the general rule that if A is a principal, G a group, and A ̃ G then (A as G) ̃ G.
The procedures Delegate and Claim are used in tandem to implement delegation; Figure 1 shows an example. Suppose process X has an Auth a that represents A, process Y has an Auth b that represents B, and X wants to give to Y an authority that represents B for A by delegation. First, X gets from Y a Prin pb that represents B. Then X calls Delegate(a, pb) to make a new Auth c that represents A but also carries the property that A says ((B | A) ̃ (B for A)). Now X sends c to Y, which receives it as the Prin pc. Finally Y calls Claim(b, pc) to get an Auth d that represents B | A, and hence B for A by the delegation axiom. Before doing this, Y may wish to call Authenticate(pc) to find out what principal d will represent.
A process can make an Auth a invalid by calling Discard. The effect is that once the receiver caches time out, the process can no longer use a to speak for a’s principal. If all is TRUE, a also becomes invalid in all the processes that have inherited it; this allows a process to take an authority away from its children, for example.
If a was the result of Delegate, invalidating it has another effect: any Auth derived from a by Claim will also become invalid within a fairly short time (at most 30 minutes). The same thing happens if the process that called Delegate terminates.
The API provides no direct access to the logical operators | and Ù or to the handoff rule.
|
|
|
Figure 2: Structure of the authentication agent |
4 The Authentication Agent
The authentication agent handles most of the complexity of authenticating requests from compound principals. It has four parts. The secure channel manager creates process-to-process secure channels. The authority manager associates Auths with processes and handles authentication requests. The credentials manager maintains credentials on behalf of local processes and validates certificates authored on other nodes. Finally, the certification library establishes a trusted mapping between principal names and cryptographic keys, and between groups and their members. Figure 2 shows the structure of the authentication agent; arrows indicate call dependencies.
Only a few changes were needed to the rest of Taos to support the authentication agent: implementing authority inheritance in the process manager; supporting secure loading; and adding Auth parameters to all security-sensitive kernel calls.
4.1 The secure channel manager
The secure channel manager implements the Chan datatype described in Section 3.1. It does not implement secure channels itself. Instead, it controls the construction of node-to-node channels, and then uses them to provide process-level channels to its clients. Since the purpose of authentication is to prove that a channel utters a request on behalf of a principal, the secure channel manager must be able to attribute channels to processes and thereby link channels to the principals for which they speak. Our design does not mandate any one technique for implementing secure channels; such techniques are well documented [13].
4.1.1 Node-to-node channels
Given two nodes A and B, it is easy to establish a shared-key channel C between them. We use the following protocol, which is described in more detail in Lampson et al. [1992, Section 4]. In brief, A invents a random number Ja and sends it to B encrypted under the public part of B’s key Kb. Similarly, B sends Jb encrypted under A’s key Ka. Note that this is encryption for secrecy rather than integrity. Now, both A and B can compute a shared key by combining Ja and Jb via a hash function. A shared key established in this fashion can be used to form a secure channel C, which speaks for Kb from A’s viewpoint and for Ka from B’s viewpoint.
The secure channel manager maintains a cache of keys shared with other nodes, indexed by node address and used to implement GetChan and Send. Another cache contains a mapping from shared keys to node keys, and is used by Receive to get from the shared key that successfully decrypts a message to a node key. Both of these caches can be flushed as necessary. In fact, both are flushed periodically in order to invalidate old keys. The key-to-node-key mapping is flushed half as often as the address-to-key mapping so as to prevent misses caused by partners using older keys.
Each node is responsible for caching and timing out the keys it shares with other nodes, and either end of a secure channel can trigger the generation of a new shared key. When B re-executes the key-establishment protocol, the resulting channel from A still speaks for Ka. Hence, rekeying does not invalidate authentication state based on node keys.
Taos does not implement hardware secure channels. The key exchange mechanism it implements is, however, suitable for constructing them. Herbison [1990] discusses the use of encrypting network controllers to build efficient secure channels. Our system design is intended to operate best with encryption-capable controllers. DES [National Bureau of Standards 1977] hardware for such controllers has been shown to operate at speeds of 1 Gbit/sec [Eberle and Thacker 1992], so performance should not be a problem.
In our implementation, software DES is used to sign channel certificates (see Section 4.3.4), but requests are made without signature to avoid the overhead of software encryption.
4.1.2 Process-to-process channels
The channels offered to clients of the API are always between two processes. These channels are formed by multiplexing process-level data across the node-to-node channels discussed in the previous section. The concrete form of the Chan datatype differs depending on the secure channel implementation. However, all channel implementations must support naming of channels by ChanIDs:
TYPE ChanID = { nk:KeyDigest; pr:INTEGER; addr:Address };
The nk field of ChanID names the node key of the partner, pr identifies the partner process, and addr indicates the address of the partner authentication agent. A message digest function is applied to node keys in order to produce small values for the nk field. We use the MD4 message digest function [Rivest 1991].
In Taos we exploit the fact that most communication employs a transport protocol under our control. We identify each process with a 32-bit process tag (PTag)[3] and mark all transmissions with the PTag of the sending process.
The secure channel manager exports the primitives:
PROCEDURE GetChanID(ch:Chan): ChanID;
PROCEDURE PTagFromChan(c:ChanID): PTag;
The receiver of a message can call GetChanID to obtain a ChanID given an abstract Chan. At the source of channel c—where c.nk is the digest of the local node key—PTagFromChan(c) can be called to derive the PTag for the process that controls c. In Taos, we put a PTag in the pr field and hence can implement GetChanID by concatenating the sender’s node key, PTag, and node address. The implementation of PTagFromChan just returns c.pr. Process-level multiplexing can also be done with standard protocol implementations such as TCP/IP and UDP/IP that use small integer port numbers to identify the origin and destination of messages within a node. Port numbers would be perfect process identifiers (that is, values of the pr field) if they were not reusable. One possible workaround is to place restrictions on the reuse of port numbers. Another is to treat process channels as secure connections that must be explicitly opened and closed; this requires considerable care.
4.2 The authority manager
The authority manager implements the operations on Auths and Prins discussed in Sections 3.2 and 3.3. The internal interface to the authority manager parallels the API quite closely. However, for each Auth supplied as an argument, the kernel call dispatcher appends the PTag of the caller. This PTag argument is used to ascertain that the caller owns each supplied Auth. We say that a process owns an Auth if the authority manager has given that process the right to use it. Whenever an Auth is explicitly returned to a process through the API, the calling process owns it.
Each new Auth is assigned a unique AID by the authority manager. In our implementation AIDs are 96 bits wide, so there is no need to reuse one. The authority manager maintains a table with credentials for the Auths it creates, indexed by AID. Each entry contains:
• credentials for the corresponding Auth,
• a list of PTags of processes that own this Auth,
• credentials for unclaimed delegations (only if this Auth resulted from a call to Delegate), and
• a source from which to refresh delegation credentials (only if this Auth resulted from a call to Claim).
The precise structure of credentials is irrelevant to the authority manager. For now, we think of them as bundles of certificates, which for example prove that a channel speaks for a principal or that a principal is another’s delegate.
Much like Unix file descriptors, Auths can be passed by inheritance to child processes. The authority manager provides two primitives that the process manager can use to implement this inheritance:
PROCEDURE Handoff(a:Auth; ptag:PTag);
PROCEDURE PurgePTagCptag: PTag);
Handoff adds ptag to the list of PTags of processes that own a. It is called when an Auth is inherited from a parent process. PurgePTag eliminates all instances of ptag in the credentials table. It is called when the process identified by ptag terminates.
4.2.1 Callbacks
As we have seen, AIDs and channels are used to represent principals in network protocols. For this to work, the authority manager must be prepared to produce credentials on behalf of any Auth it manages. These credentials are obtained with callbacks to save the cost of passing complex credentials repeatedly. In fact, credentials are generated lazily, only when needed, and AIDs may be passed before the corresponding credentials exist. Although credentials could easily be bundled with requests, they are large enough (> 1 kbyte) to affect communications performance. Since the results of authentication are cached extensively, callbacks improve performance for nearly all applications, even in high-latency networks.
Suppose a user-level process receives a request on a channel ch. In this case, the API function GetPrin returns a Prin p constructed from GetChanlD(ch) and the AID accompanying the request. Now the process can ask its authentication agent to resolve p into a principal name, for example with a call to Authenticate(p). We use the PrinID datatype to represent Prins that are passed across address-space boundaries (for instance between user space and the authentication agent):
TYPE PrinID = { ch:ChanID; aid:AID };
The implementation of Authenticate(p) asks the requester’s agent (at p.ch.addr) to provide credentials for p. This agent looks up p.aid in its credentials table and determines whether PTagFromChan(p.ch) specifies a process that owns the corresponding Auth. If it does, the requester’s agent returns a channel certificate as proof that the channel speaks for the principal that p represents. This proof consists of the credentials found in p.aid’s credentials-table entry and a statement that p.ch quoting p.aid speaks for the principal (see Section 4.3.1).
It is critical for performance that the results of Authenticate be cached. Caching can be implemented in user space, in the operating system, or both. Our implementation caches the results of authentication callbacks in user space, with a timeout equal to the validity interval of the supplied channel certificate up to a maximum of 30 minutes.
A callback also occurs when a call Claim(me, p) activates a delegation. The delegate’s authentication agent passes p in a callback to the delegator’s agent, which uses p.aid to find credentials suitable for signing a delegation certificate and returns a signed certificate to the delegate’s agent. That agent must remember p so that it can repeat the callback to refresh the delegation in case it expires. The delegation certificate need not be concealed. Any agent may request a copy, since it is useful only to the delegate’s agent.
4.3 The credentials manager
The credentials manager is the heart of the Taos authentication system. Its primary functions are to build, check, and store credentials. We explain the form of credentials and their logical meaning in the first two subsections. Then we give the interface to the credentials manager and discuss techniques for avoiding signatures.
4.3.1 Credentials
We understand credentials as having logical meanings. A credential is evidence that one principal Q speaks for another principal P. If the credential were written as a formula M, its recipient would want to check that M implies Q ̃ P.
Taos encodes credentials as S-expressions. The encoding is designed to make straightforward the proof of the theorem that M implies Q ̃ P. If an S-expression is a well-formed credential, then there is a simple procedure for extracting P and Q from it that ensures that M implies Q ̃ P. If in addition all signatures in the S-expression are recent and correct, then the S-expression is said to be valid; the S-expression is interpreted as M only if it is valid. Thus, deriving Q ̃ P is reduced to parsing a credential and checking signatures.
In this section we define our S-expression grammar for credentials. In Section 4.3.2 we give a table of correspondences between S-expressions and logical formulas, effectively recovering the logical form of a credential from the S-expression encoding. This logical form is used only in explaining our implementation; the implementation does not manipulate formulas. We also describe how to check whether a credential is valid.
Table 1 gives the grammar for credentials. Names, keys, PrinDs, and signatures are terminals. The main production is the one for channel, because requests always arrive on channels. The name components of primary credentials are only hints, used to simplify the mapping of keys into names. We say that a credential y is embedded in a credential x if y is a subexpression of x.
|
channel = ( ‘channel’ prin prinID signature ) boot = ‘boot’ k_as key signature ) login = (‘login’ k_as session signature ) session = (‘session’ key boot signature ) delegation = (‘for’ delegator delegate signature ) p_as = ( ‘as’ prin role ) | primary k_as = ( ‘as’ k_as role ) primary = ( key name ) prin = boot | login | delegation | p_as delegator = prin delegate = prin role = name |
|
Table 1: Grammar for credentials |
A certificate is an instance of one of the first group of rules in the credentials grammar. The signature in a certificate includes the interval of time for which it is valid plus an unforgeable value identifying the signer. This value is a MD4 digest of the certificate, encrypted by a RSA secret key [Rivest et al. 1978]. The digest is computed over the entire certificate, excluding embedded signatures, by a one-way function that reduces its input to a size small enough to sign conveniently; the function is one-way in the sense that it is computationally hard to find a different input with the same digest.
We now discuss specific credentials in some detail. For each type of signed credential we discuss an example, borrowing context from Section 2.2.
Boot certificates. A boot certificate describes a handoff from a machine key to a node key. In our example, the meaning M of the boot certificate is:
(Kvax4 as OS) says (Kws ̃ (Kvax4 as OS)) (8)
From M and the handoff axiom, we obtain:
Kws ̃ (Kvax4 as OS)
which is the formula Q ̃ P in this case. The boot certificate is encoded as:
(boot (as (Kvax4 Vax4) OS) Kws sig1)
Login and session certificates. A login certificate is a special form of delegation certificate. It denotes a delegation from a user’s key to the conjunction of a node key with a temporary session key. The user’s key should be in memory for the shortest possible time, to reduce the chance that the key will be discovered by an attacker. In Taos, it is present just long enough to sign the login certificate. This certificate is of long duration, on the order of days. More sophisticated login protocols that take advantage of smart-cards can produce equivalent login certificates [Abadi et al. 1993a].
The node key and the session key are combined in a session certificate, which represents a handoff from the session key to the node key. A session certificate has a short timeout and is refreshed as needed until the end of the session. When the session ends, the session key is discarded so that the session certificate can no longer be refreshed. Because the login certificate delegates to the node key and to the session key, the certificate becomes unusable at the end of the session; the inclusion of the session key compensates for the long timeout of the login certificate.
In our example, Bob, with key Kbob, logs in to WS. We still have the boot certificate (8). Let Ks be the session key; the session certificate adds:
Ks says ((Kvax4 as OS) ̃ Ks) (9)
and the login certificate adds:
Kbob says ((P1 | Kbob) ̃ (P1 for Kbob)) (10)
where P1 is ((Kvax4 as OS) Ù Ks). From the conjunction of formulas (8), (9), and (10), we can derive:
(Kws | Kbob) ̃ (P1 for Kbob)
In the notation introduced above, the conjunction is M, and the principals (Kws | Kbob) and (P1 for Kbob) are Q and P, respectively.
In our encoding the session certificate is embedded inside the login certificate, and the boot certificate inside the session certificate:
(login
(Kbob Bob)
(session Ks (boot (as (Kvax4 Vax4) OS) Kws sig1) sig2)
sig3)
The embedded certificates identify the machine, the node, and the session key, and give credentials for them.
General delegation certificates. The general form of delegation involves transfer of rights between principals. Continuing the example, suppose that Bob on WS delegates to a node (Vax5 as OS). The formula that corresponds to this delegation is:
(Kws | Kbob) says ((P3 P2) ̃ (P3 for P2))
where P2 is (P1 for Kbob) and P3 is (Kvax5 as OS). Conjoining this formula with those for Bob’s login (8), (9), and (10), and with the boot certificate for (Vax5 as OS):
(Kvax5 as OS) says (Kws' ̃ (Kvax5 as OS))
we can prove:
(Kws' | Kws | Kbob) ̃ (P3 for P2)
In our encoding the entire delegation certificate is:
(for
(login... sig3)
(boot (as (Kvax5 Vax5) OS) Kws' sig4)
sig5)
The login certificate given above is nested here in its entirety (abbreviated with an ellipsis) and used as the source of a delegation. The delegate is the boot certificate for Vax5 as OS.
Channel certificates. Ultimately, channels are the only principals that make requests directly. A request on a channel is attributed to a principal that has handed off some of its rights to the channel. A channel certificate represents this handoff. In our system, each certificate authenticates a channel multiplexed on a node-to-node key. More precisely, the channel is a node-to-node channel quoting a process quoting an AID. Its encoding is a textual representation of the PrinID datatype from Section 4.2.
In our example, a channel certificate for a channel Cbob from Bob means:
(Kws | Kbob) says (Cbob ̃ P2)
Conjoining this formula with those for Bob’s login (8), (9), and (10), we can now prove:
Cbob ̃ P2
When Cbob is the channel key47 | ptag13 | aid42, this certificate is encoded as:
(channel
(login... sig3)
key47 ptag13 aid42
sig4)
Because channels are typically short-lived, a channel certificate normally has a short validity interval.
4.3.2 The meanings of credentials
As the previous examples suggest, each valid credential x in the grammar has a logical meaning M(x). Now we define M in general. Since M is a function, the mapping from S-expressions to formulas is clearly unambiguous. We define validity later in this section.
It is convenient to use several auxiliary functions. A function I gives us the immediate meaning of a credential. Then M(x) is defined to be I(x) conjoined with I(y) for every credential y embedded in x. Thus, the interpretation of a credential is its immediate meaning, plus the meaning of any embedded credentials. In the cases of primary, p_as, and k_as credentials, which bear no signature, I(x) is simply true. In the other cases, I(x) is the assertion made by the top-level signature; it does not refer to other signatures or their timestamps, and has the form
S(x) says (T(x) ̃ P(x))
where P(x) and T(x) are principals and S(x) is the speaker, the principal that issues the credential. In particular, when S(x) is a key, it is the key that should be used in the credential’s signature.
In each case, the purpose of a credential x is to establish that Q(x) speaks for P(x). More precisely, the formula M(x) should imply Q(x) ̃ P(x). For example, a boot certificate x of the form
(boot (Kvax4 Vax4) Kws signature)
means Kvax4 says (Kws ̃ Kvax4); this formula is M(x). Let Q(x) be Kws and P(x) be Kvax4; by the handoff axiom, M(x) implies Q(x) ̃ P(x). In general, we have:
|
x |
S(x)
|
T(x)
|
P(x)
|
Q(x) |
|
boot |
Q(x.k_as)
|
x.key
|
P(x.k_as)
|
x.key
|
|
session |
x.key
|
P(x.boot)
|
x.key
|
Q (x.boot)
|
|
login |
Q(x.k_as)
|
(P( x.s.boot) Ù P(x.s)) |
(P( x.s.boot) Ù P(x.s))
|
Q(x.s.boot)
|
|
dele-gation |
Q(x.d’gator)
|
P(x.d’gate)
|
P(x.d’gate)
|
Q(x.d’gate)
|
|
channel |
Q(x.prin)
|
x.prinID
|
P(x.prin)
|
x.prinID
|
|
p_as |
|
|
P(x.prin) as x.role
|
Q(x.prin) as x.role |
|
k_as |
|
|
P(x.k_as) as x.role
|
Q(x.k_as) as x.role
|
|
primary |
|
|
x.key
|
x.key
|
|
The immediate meaning I(x) of a credential x is S(x) says (T(x) ̃ P(x)) when S(x) is defined, and true otherwise.
The meaning M(x) of a
credential x
is the conjunction of I(x) with the immediate meanings of
any credentials embedded in x. In all cases, M(x) implies Q(x) ̃ P(x). We abbreviate session by s. |
||||
|
Table 2: The logical meaning of credentials |
||||
Theorem 1. For every credential x, it is provable that
if M(x) then Q(x) ̃ P(x)
proof. We prove the theorem by induction on the structure of credentials. We use different strategies in the cases that correspond to credentials with top-level signatures and those that do not.
When x is a credential with a top-level signature, in order to derive Q(x) ̃ P(x) from M(x) it suffices to obtain both of the following:
1. Q(x) ̃ T(x), and
2. if S(x) says (T(x) ̃ P(x)) then T(x) ̃ P(x).
In all cases (1) will be a consequence of the meanings of embedded credentials. To obtain (2), we may use either
• S(x) ̃ P(x), and then the handoff axiom applies; or
• P(x) is B for A and T(x) is B | A for some A and B such that S(x) ̃ A, and then the delegation axiom applies.
As we show in the Appendix, the definitions of Table 2 satisfy these properties. The cases of credentials without top-level signatures are mostly straightforward; we treat them in the Appendix as well. □
A credential is valid if all the signatures it contains are well-formed, timely, and performed with the proper key. The proper key K for signing a certificate x is defined from S(x), with a clause for each of the possible forms of S(x):
• The proper key for a principal of the form A as R or A | A' is the proper key for A, since it is A that must apply the signature.
• The proper key for a key is the key itself.
In general, K is the key that the principal S(x) uses. If x is valid, then it has recently been signed with S(x)’s key K, so we can interpret x as a formula I(x) of the form S(x) says (T(x) ̃ P(x)). By convention, S(x) should use K to sign x only when S(x) supports T(x) ̃ P(x). This is the justification for our logical reading of valid credentials.
An obvious generalization of this definition of validity allows any key that speaks for K to sign the certificate. The generalization is used in Section 4.3.4 to allow channel certificates to be signed with DES keys.
Theorem 1 guarantees that validating a credential x suffices to show that Q(x) ̃ P(x): if x is valid, then it is interpreted as M(x) and the theorem applies. Corollary 2 makes this claim precise:
Corollary 2. For every certificate y, assume that S(y) says (T(y) ̃ P(y)) is true for the validity interval of y if the proper key signs y. Let x be a valid credential. Then Q(x) ̃ P(x) is true.
proof. If x is valid, then each certificate y embedded in x is valid: y is signed with the proper key and its validity interval includes the present. By our hypothesis, S(y) says (T(y) ̃ P(y)) is true; that is, I(y) is true. If x itself bears a signature, then similarly S(x) says (T(x) ̃ P(x)) is true. Therefore, M(x) is also true, as M(x) is the conjunction of I(x) with I(y) for each y embedded in x. By Theorem 1, Q(x) ̃ P(x) is true. □
4.3.3 The Credentials interface
The credentials manager exports the Credentials interface to the authority manager. This interface defines an abstract type CredT that represents credentials, as well as procedures for constructing CredTs and for signing and validating channel certificates. A CredT defines a principal P that can make requests, and contains an expression in the credentials grammar sufficient to prove that some other principal can speak for P.
The credentials manager holds a CredT representing the credentials for the node. Although the Firefly lacks the firmware necessary to generate a node key securely, Taos imitates secure booting by generating a boot certificate and node key at system-startup time. The node’s CredT contains this certificate and key.
The operations on credentials are:
TYPE Cred = TEXT;
PROCEDURE New(name, password: TEXT): CredT;
PROCEDURE AdoptRole(t:CredT; role:TEXT): CredT;
PROCEDURE Sign(t:CredT; p:PrinID): Cred;
PROCEDURE Validate(cr:Cred; p:PrinID): TEXT;
PROCEDURE Extract(cr:Cred): Cred;
PROCEDURE SignDel(t:CredT; cr:Cred): Cred;
PROCEDURE ClaimDel(t:CredT; cr:Cred): CredT;
Each value of the Cred datatype contains a textual representation of credentials according to the grammar of Table 1.
New produces a CredT containing a login certificate and a session key. The CredT returned by AdoptRole contains credentials for t as role.
The authority manager uses Sign to produce channel certificates in response to authentication callbacks. Similarly, it uses Validate to check the results of authentication callbacks and return principal names. Extract strips off an outer-level channel certificate, and returns the credentials of the principal for which the channel speaks.
The delegator’s authority manager implements Delegate by finding and validating a channel certificate for the delegate. It then calls Extract to get the delegate’s credentials, and stores the result. The delegate’s authority manager implements Claim by asking the delegator’s agent for a delegation certificate (produced with SignDel) and using it to call ClaimDel. The result is a CredT representing delegate for delegator.
4.3.4 Signature techniques
We use three techniques to minimize the number of public key encryptions required to sign certificates:
• As described in Section 4.1, we can establish a shared key K between two nodes A (with key Ka) and B so that B believes that K speaks for Ka. Therefore, A can sign certificates about channels to B by encrypting with K instead of Ka. Only B need believe these certificates. DES encryption (under K) is much faster than RSA encryption (under Ka).
• When one process delegates to another on the same node, it is possible to avoid one signature. The delegation certificate structure remains the same, but no cryptographic signature is needed. If an off-node delegation follows, the signature of the outer certificate implies validity for the inner one, because both use the same key.
• When refreshing nested certificates, care must be taken not to invalidate higher-level signatures. It is sufficient to omit nested signatures from the certificate digests. For example, when a session certificate is refreshed, its validity times are changed. An enclosing login certificate can avoid refresh only if its digest omits the nested signature. This omission is safe since there is no mention of nested signatures in the immediate meaning of credentials.
4.4 The certification library
If ACLs contained public keys instead of human-sensible names, network security would be considerably less complex. Unfortunately, keys are big numbers that are too unwieldy for human users to manipulate. Moreover, at the highest level, computer security applies to names for people and resources. At some point there needs to be a trusted mapping from keys to the principal names they represent. Similarly, there need to be trusted mappings from group members to group names and from image digests to role names.
The task of the certification library is to implement these mappings. We also use it to recover keys from stable storage given passwords short enough for people to remember. Our certification authority (or CA, see Section 2.2) is a simple program that manages the database underlying these services. This CA is off-line in the sense that clients need not communicate with it in real time in order to trust its statements. A CA that could function without any network connections might be an interesting addition to our work. For example, we could use a portable computer to write certificates, keep the computer in a safe, and allow floppy disks as the only means of communication with the rest of the world.
Bootstrapping trust. A practical system of any size must base trust on shared knowledge of a trusted CA. In Taos, this information takes the form of a CA public key. Certificates signed with this key are trusted. It is crucial to protect the corresponding secret key.
A user learns his own secret key and the public key of his trusted CA by decrypting a user-specific string stored in the name server.[4] This string contains the user’s private data encrypted under a DES secret derived from the user’s password. We keep analogous strings for nodes. Storing user secrets in this way would not be necessary if users carried public key smart-cards [Abadi et al. 1993a; Quisquater et al. 1991].
Name certificates. These describe a mapping from keys to names. They are signed by a CA trusted for this purpose, much like CCITT X.509 certificates [CCITT 1988]. The logical form of a certificate that maps Ku to U is:
Kca says (Ku ̃ U)
A simple extension of the grammar described in the previous section is used to express these statements.
Since certificates are statements signed off-line, they can be believed even if retrieved from untrusted storage. In Taos, we use a replicated, highly available name service [Birrell et al. 1993] to store name certificates. Certificates are indexed by name in this store. The replication makes a denial-of-service attack more difficult.
We may now continue the example of Section 4.3.1. Given valid name certificates that map Kbob to Bob and Kvax4 to Vax4, we obtain:
Cbob ̃ ((Vax4 as OS) for Bob)
Therefore, when a request appears on the channel Cbob, it is attributed to (Vax4 as OS) for Bob.
Membership certificates. These state that a principal U speaks for (is a member of) a group G:
Kca says (U ̃ G)
They are used in Taos ACL checking, and also in role processing and secure loading.
Image certificates. These are used in secure loading to verify the executable image of a recently loaded program and to name the role under which that program should run. The purpose of an image certificate is to establish that a given image digest I speaks for a role name R:
I ̃ R
(Think of R as the name of a program like emacs, or of a class of programs like games.) It would be sufficient for the CA to produce an image certificate:
Kca says (I ̃ R)
Instead, the CA permits a user U to write an image certificate for R. The CA issues:
Kca says ((U | R-owner) ̃ R)
where R-owner is a special name associated with R (e.g., emacs-owner with emacs). If Ku is U’s key, we obtain:
(Ku | R-owner) ̃ R
This means that U can release a new version of R with digest I by signing an image certificate:
Ku says R-owner says (I ̃ R)
and then I ̃ R follows.
Image digests can be computed using any secure one-way function. Taos stores image certificates as a file property on certain executable files.
4.4.1 The CertLib interface
The certification library exports the procedures:
PROCEDURE CheckKey(name:TEXT; k:Key): BOOL;
PROCEDURE IsMember(name, group: TEXT): BOOL;
PROCEDURE CheckImage(d:Digest; prog, cert:
TEXT);
The credentials manager calls CheckKey to find and validate a name certificate that states that k speaks for name. The IsMember procedure ascertains whether name is a member of group. Checklmage supports secure loading. It checks that the certificate cert states that the image digest d speaks for the program prog, and that cert is signed by a principal with control of images for prog.
4.5 Simplifying compound names
An authentication result in Taos is more often than not a compound principal. The principals that result from credential validations have the form:
principal = name
|
(principal for principal)
|
(principal as role)
where name and role are strings. Existing applications often deal only with simple names. The following function reduces a principal to a simple name:
• If the principal has a simple name, return it.
• If the principal is B for A, apply this function recursively to A. (Checks can easily be added to guarantee that B is trustworthy.)
• If the principal is A as R, then apply this function recursively to A. Take the resulting simple name, and find a membership certificate stating that it speaks for R. If successful, then return R, otherwise fail.
For example, WS for Bob reduces to Bob, and WS for (Bob as Admin) reduces to Admin if Bob ̃ Admin (that is, if Bob is a member of Admin).
5 Experience
The authentication system described in this paper was in daily use for a year by a community of nearly 80 researchers and administrative personnel. In this section we discuss our experience, and in particular the performance of our system.
5.1 Authentication for the Echo file system
The most commonly used authenticated application was Echo [Birrell et al. 1993], a distributed file system used extensively within Taos. The Echo environment exercised all the Taos security features described in this paper except general delegation.
In addition to authenticating normal file system operations, Echo allowed the use of roles to control access to protected parts of the file system namespace. Users typically logged onto the system with the role “normal user”, which indicated that they had no special privileges. Administrators had the option of taking on other roles when they wanted to access sensitive files. Using these roles for system administration is more precise and less dangerous than using a special super-user account with unqualified privileges (like root under Unix).
It is often useful for a user to run programs with some of the rights of a node. For example, a program might need control over all the node’s processes, or over the node’s configuration files and working space. We used secure loading to allow normal users to run certain programs with enhanced rights.
5.2 Gateways
We built a gateway that allows ordinary NFS clients to access the Echo file system. It uses standard methods to determine the principal p making an NFS request and then forwards the request to Echo. If the gateway runs as the principal G, then it can utter forwarded requests as G | p. We could have allowed the principal G | p in Echo ACLs. Instead, for each p we invent a name q, issue a certificate Kca says ((G | p) ̃ q), and then use q on ACLs for authorizing forwarded requests from p. In some systems q is called a proxy.
This approach can be applied to accept messages authenticated by any other protocol. The tricky part is finding a place to put the gateway where it can intercept and translate the authentication protocol, which is often application-specific.
To go in the other direction and translate one of our authenticated messages p says m into another protocol, say Kerberos, the gateway would have to be able to authenticate itself as p in Kerberos. To achieve this, it would need either to have the user’s password for long enough to obtain a Kerberos ticket-granting ticket, or to act itself as a Kerberos authentication server. We have not tried to implement this.
5.3 Performance
The performance of our system depends on the costs of the cryptographic operations:
|
RSA sign |
RSA verify |
DES |
MD4 |
|
248 ms |
16 ms |
15 ms |
6 ms/kbyte |
Our RSA implementation [Shand and Vuillemin 1993] is carefully
coded in C and assembler. We use a 512-bit modulus and a public key exponent of
3. The Firefly has 4 CVax processors, each running at about 2.5 MIPS. Our
multiprocessor implementation of RSA signatures gains nearly a factor of two in
speed. With only a single processor, it takes 472 ms to compute a RSA
signature; this compares with 68 ms on a DECstation 5000, which runs at 20
MIPS. We use public-domain implementations of MD4 and DES (in C); much faster
ones are possible [Lampson et al. 1992, Section 4].
Efficient RSA key generation is also important to our implementation. Using three separate threads running a randomized prime generation algorithm [Knuth 1981, p. 388], we can produce a new RSA key in 10-15 seconds.[5] Only two primes are needed for generating a key, but there is a large variance in the time required for generating a prime. Using three threads significantly reduces the average time required for generating two primes.
|
|
Auth |
Delegate |
Auth |
|
|
login |
|
delegation |
|
RSA sign |
— |
1 ´ 248 ms |
— |
|
RSA verify |
3 ´ 16 ms |
10 ´ 16 ms |
7 ´ 16 ms |
|
DES |
2 ´ 15 ms |
2 ´ 15 ms |
2 ´ 15 ms |
|
MD4 |
6 ms |
18 ms |
12 ms |
|
S-expr |
46 ms |
165 ms |
91 ms |
|
RFC |
2 ´ 5 ms |
3 ´ 5 ms |
2 ´ 5 ms |
|
Total |
140 ms |
636 ms |
255 ms |
|
Measured |
143 ms |
671 ms |
276 ms |
|
Table 3: Authentication test timings |
|||
In Table 3 we show the results of measuring three basic authentication operations. The numbers assume an existing node-to-node secure channel and a loaded name certificate cache. We show how time is divided between cryptographic functions and other parts of the system. We estimate that RFC with non-trivial arguments takes on the order of 5 ms [Schroeder and Burrows 1990]. The line labeled “S-expr” indicates the cost of parsing and writing S-expressions. This cost is about one-third of the total, but it could easily be reduced.
The first column of the table (Auth-login) shows the time required for the first authenticated RFC—subsequent calls to the same server using the same credentials will get cache hits. The caller’s credentials are those for a simple login session. This test includes a callback to the caller’s agent and a subsequent channel-certificate validation. We expect this cost to be incurred infrequently: for example, when the user’s machine first contacts a file server, and whenever the credentials need refreshing thereafter (every 30 minutes).
The second test (Delegate) measures the time taken for a logged-in user to delegate to a logged-in user on another node. Delegation requires a hidden authentication, and hence three RPCs rather than two.
The final test (Auth-delegation) is similar to the first (Auth-login), except that the caller’s credentials involve an additional delegation. Once again, the costs shown are incurred only on the first use of the credentials and each time the cache is refreshed.
There are two important facts to be gleaned from Table 3. First, the cost of using credentials to make requests is considerably less than that of delegation. This is good, since delegations occur much less frequently than requests. Second, almost all of the component costs of authentication are compute-intensive. Moving to a faster processor should improve the actual performance linearly. The Auth-login test should take less than 25 ms on a DECstation 5000.
Even with faster processors, it is clear that caching at several levels is essential to system performance:
• The cache used to implement Authenticate prevents repeated authentication callbacks. It has a timeout of roughly 30 minutes, so there are at most two authentication callbacks to an Echo client in a 30-minute interval, regardless of the number of file system operations performed.
• The shared key cache in the secure channel manager prevents unnecessary key exchanges. The keys stored there expire with a much longer period (6 hours).
• The certification library maintains a cache that saves the results of name certificate validations. There a cached result can remain valid until the certificate expires, although we flush results more frequently to speed up revocation.
Further caching is clearly possible. For example, the meanings of common embedded credentials (such as boot certificates) might be cached.
5.4 Scale
Although our implementation was not used on a large scale, the technique of off-line certification with minimal reliance on on-line services is well suited to large naming hierarchies [Lampson et al. 1992, Section 5.2]. The performance of our basic security primitives is dependent on system scale only in the cost of fetching static certificates such as those for names and group memberships. In our implementation, this cost is only a small fraction of the total overhead. While this cost might grow with the number and geographic distribution of certified users, it can be offset by caching, hierarchical certification, and database replication.
Our design can accommodate fast revocation of name certificates along the lines discussed elsewhere [Abadi et al. 1993b; Lampson et al. 1992], but we have not implemented this feature. There is an inherent tradeoff between timely revocation and the effectiveness of caching. This tradeoff becomes more significant as the scale of the system increases.
6 Conclusion
We have described a framework for security in distributed systems that is based on logic. The logic takes shape in an operating system that was in daily use by a substantial community. Our system employs compound credentials to express the complex relationships between users, machines, and programs, yet little of this complexity shows through to users and programmers. Moreover, the careful optimizations that surround our use of public key cryptography ensure that it does not hurt performance.
We have explained our system in logical terms, and in particular obtained a theorem that relates concrete credentials and their logical meanings. It would be interesting to obtain further theorems to prove the correctness of our implementation. Even stating the proper results remains a challenge.
The need for well-founded and expressive distributed security systems will grow with the speed of processors and networks, the number of interconnected entities, and the complexity of applications. Our work shows how to design practical systems that meet this need and demonstrates that such systems can be built and can perform well.
Acknowledgements
Andrew Birrell, Morrie Gasser, Andy Goldstein, and Charlie Kaufman were at the origin of many of the ideas discussed here. Allan Heydon, Roy Levin, Tim Mann, Roger Needham, and Mike Schroeder all suggested improvements in the presentation of this paper.
Appendix
In this appendix we complete the proof of Theorem 1.
First we treat the cases of credentials with top-level signatures, following the strategy described in Section 4.3.2.
• boot:
(1) Q(x) ̃ T(x), since in this case both Q(x) and T(x) equal x.key.
(2) S(x) ̃ P(x), since S(x) is Q(x.k_as) and P(x) is P(x.k_as), and Q(x.k_as) and P(x.k_as) are always equal.
• session:
(1) Since x.boot is embedded in x, the induction hypothesis guarantees that M(x.boot) implies Q(x.boot) ̃ P(x.boot), that is, Q(x) ̃ T(x). Further, M(x) implies M(x.boot) and hence Q(x) ̃ T(x).
(2) S(x) ̃ P(x), since both S(x) and P(x) equal x.key.
• login:
(1) Since x.s.boot is embedded in x, the induction hypothesis guarantees that M(x.s.boot) implies Q(x.s.boot) ̃ P(x.s.boot). Similarly, M(x.s) implies Q(x.s) ̃ P(x.s). By definition Q(x.s) equals Q(x.s.boot), so M(x.s) implies Q(x.s.boot) ̃ P(x.s). Therefore, the conjunction of M(x.s.boot) and M(x.s) implies Q(x.s.boot) ̃ (P(x.s.boot) Ù P(x.s)). Since Q(x.k_as) and P(x.k_as) are equal and | is monotonic, this conjunction also implies (Q(x.s.boot) Q(x.k_as)) ̃ ((P(x.s.boot) Ù P(x.s)) | P(x.k_as)), that is, Q(x) ̃ T(x). Finally, M(x) implies both M(x.s.boot) and M(x.s), and hence Q(x) ̃ T(x).
(2) P(x) is of the form B for P(x.k_as) and T(x) of the form B P(x.k_as). Moreover, S(x) is Q(x.k_as), which equals P(x.k_as).
• delegation:
(1) Since x.delegate and x.delegator are both embedded in x, the induction hypothesis guarantees that M(x.delegate) implies Q(x.delegate) ̃ P(x.delegate). Similarly, M(x.delegator) implies Q(x.delegator) ̃ P(s.delegator). Since | is monotonic, the conjunction of M(x.delegate) and M(x.delegator) implies (Q(x.delegate) | Q(x.delegator)) ̃ (P(x.delegate) | P(x.delegator)) that is, Q(x) ̃ T(x). Finally, M(x) implies both M(x.delegate) and M(x.delegator), and hence Q(x) ̃ T(x).
(2) P(x) is of the form B for P(x.delegator) and T(x) of the form B | P(x.delegator). Moreover, S(x) is Q(x.delegator) and we have proved Q(x.delegator) ̃ P(x.delegator) using the induction hypothesis.
• channel:
(1) Q(x) ̃ T(x), since in this case both Q(x) and T(x) equal x.prinID.
(2) Since x.prin is embedded in x, the induction hypothesis guarantees that M(x.prin) implies Q(x.prin) ̃ P(x.prin), that is, S(x) ̃ P(x). Further, M(x) implies M(x.prin) and hence S(x) ̃ P(x).
The remaining cases correspond to credentials with no top-level signature. They are simpler:
• p_as: Since x.prin is embedded in x, the induction hypothesis guarantees that M(x.prin) implies Q(x.prin) ̃ P(x.prin). Therefore, by the monotonicity of as, M(x.prin) implies (Q(x.prin) as x.role) ̃ (P(x.prin) as x.role), that is, Q(x) ̃ P(x). Finally, M(x) implies M(x.prin) and hence Q(x) ̃ P(x).
• k_as: There are two cases depending on whether x is simply a primary or contains a role. In the former case, Q(x) ̃ P(x), since both Q(x) and P(x) equal x.key. In the latter case, x.k_as is embedded in x, and hence the induction hypothesis guarantees that M(x.k_as) implies Q(x.k_as) ̃ P(x.k_as). Therefore, by the monotonicity of as, M(x.k_as) implies (Q(x.prin) as x.role) ̃ (P(x.prin) as x.role), that is, Q(x) ̃ P(x). Finally, M(x) implies M(x.k_as) and hence Q(x) ̃ P(x).
• primary: Q(x) ̃ P(x), since in this case both Q(x) and P(x) equal x.key.
References
[1] Abadi, M., Burrows, M., Kaufman, C., and Lampson, B. Authentication and delegation with smart-cards. Science of Computer Programming 21, 2, Oct. 1993, 93-113.
[2] Abadi, M., Burrows, M., and Lampson, B., and Plotkin, G. A calculus for access control in distributed systems. ACM Trans. Prog. Lang. and Sys. 15, 4, Oct. 1993, 706-734.
[3] Birrell, A., Hisgen, A., Jerian, C., Mann, T., and Swart, G. The Echo distributed file system. Report 111, Systems Research Center, Digital Equipment Corp., Aug. 1993.
[4] CCITT. Information processing systems—Open systems interconnection—The directory authentication framework. CCITT 1988 Recommendation X.509.
[5] Eberle, H. and Thacker, C. A 1 Gbit/second GaAs DES chip. Proc. IEEE Custom Integrated Circuit Conf., 1992, 19.7.1-19.7.4.
[6] Gasser, M., Goldstein, A., Kaufman, C., and Lampson, B. The Digital distributed system security architecture. Proc. 12th National Computer Security Conference, NIST/NCSC, 1989, 305-319.
[7] Herbison, B. Low cost outboard cryptographic support for SILS and SP4. Proc. 13th National Computer Security Conference, NIST/NCSC, 1990, 286-295.
[8] Knuth, D. The Art of Computer Programming, volume 2, second ed., Addison-Wesley, 1981.
[9] Kohl, J. and Neuman, C. The Kerberos Network Authentication Service. Internet RFC 1510, September 1993.
[10] Lampson, B., Abadi, M., Burrows, M., and Wobber, E. Authentication in distributed systems: Theory and practice. ACM Trans. Comp. Sys. 10, 4, Nov. 1992, 265-310.
[11] Lampson, B. Protection. ACM Operating Systems Review 8, 1, Jan. 1974, 18-24.
[12] National Bureau of Standards. Data Encryption Standard. FIPS Pub. 46, Jan. 1977.
[13] Needham, R. Cryptography and Secure Channels. Distributed Systems, 2nd ed., S. Mullender (editor), ACM Press, 1993, 231-241.
[14] Open Software Foundation Introduction to OSF DCE, Revision 1.0, Dec. 1992.
[15] Quisquater, J.-J., de Waleffe, D., and Bournas, J.-P. Corsair: a chip card with fast RSA capability. Smart Card 2000, D. Chaum (editor), Elsevier, 1991, 199-206.
[16] Rivest, R., Shamir, A., and Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Comm. ACM 21, 2, Feb. 1978, 120-126.
[17] Rivest, R. The MD4 message digest algorithm. Advances in Cryptol-ogy: Crypto ‘90, Springer-Verlag LNCS, 1991, 303-311.
[18] Schroeder, M. and Burrows, M. Performance of Firefly RPC. ACM Trans. Comp. Sys. 8, 1, Feb. 1990, 1-17.
[19] Shand, M. and Vuillemin, J. Fast implementations of RSA cryptography, 11th Symposium on Computer Arithmetic, IEEE Computer Society, 1993.
[20] Thacker, C., Stewart, L., and Satterthwaite, E. Firefly: A multiprocessor workstation. IEEE Trans. Computers 37, 8, Aug. 1988, 909-920.