The ABCDs of Paxos
Replicated state machines
Consensus: a set of processes decide on an input value
Paxos asynchronous consensus algorithm
AP Abstract Paxos: generic, non-local version
CP Classic Paxos: stopping failures, compare-and-swap
1989: Lamport, Liskov and
Oki
DP Disk
Paxos: stopping failures,
read-write
1999: Gafni and Lamport
BP Byzantine
Paxos: arbitrary failures
1999: Castro and Liskov
The paper is at research.microsoft.com/lampson
Replicated State Machines
Lamport 1978: Time, clocks and the ordering of events …
Cast your problem as a deterministic state machine
Takes client input requests for state transitions, called steps
Performs the steps
Returns the output to the client.
Make n copies or ‘replicas’ of the state machine.
Use consensus to feed all the replicas the same inputs.
Steps must be deterministic, local to replica, atomic (use transactions)
Recover by replaying the steps (like transactions)
Even a read needs a step, unless the result is “as of step n”.
Applications of RSM
Reliable, available data storage system
Airplane flight control
Reflexive: Changing quorums of the consensus algorithm
Issuing a lease:
A lock on part of the state that times out, hence is fault tolerant
Leaseholder can work on its state without consensus
Like any lock, a lease can have modes or be hierarchical
The Idea of Paxos
A sequence of views; get a decision quorum in one of them.
Each view v chooses an anchored value cv: equals any earlier decision.
If a quorum accepts the choice, decision!
Decision is irrevocable,
may be invisible, but is any later
view’s choice.
Choice
is changeable, must be visible

Design Methodology
· Communicate only stable predicates: once true always true
· Structure program as a set of atomic actions
· Make actions as non-deterministic as possible: weakest guards
Allows more freedom for the implementation
Makes it clear what is essential
· Separate safety, liveness, and performance
Safety first, then strengthen guards for liveness and scheduling
· Abstraction functions and simulation proofs
Notation
Subscripts and superscripts for function arguments: rva for r(v,
a)
State functions used like variables
Actions described like this:
|
Name |
Guard |
State change |
|
Closev |
cv = nil Ù x Î anchorv |
→cv := x |
Failure Model
A set M of processes (machines)
A faulty process can send arbitrary
messages: F m
A stopped process does nothing: S m
A failed process is faulty or stopped. Failure doesn’t lose state.
Limits on failure:
ZF = set of sets of processes that can all be faulty
ZS = set of sets of processes that can all be stopped
ZFS = set of sets of processes that can all be failed
Examples:
Fail-stop: n processes, ZF={}, ZS=ZFS=any set of size < (n+1)/2
Byzantine: n
processes, ZF = ZS=ZFS=any set of size < (n+1)/3
Intel-Microsoft: nI + nM processes, ZF=any subset of one side
Quorums and Predicates
Quorum: monotonic set of sets of processes: q in Þ any superset in.
Predicates g. Predicates on processes G, so Gm is a predicate.
A stable predicate once true remains true.
A predicate G
holds in a quorum Q: Q#G = {m | Gm Ú Fm} Î
Q
Shorthand: Q[rv*=x] for Q#(λ m | rvm = x).
A good quorum is not all faulty: Q~F = {q | q Ï ZF}
Q and Q′ exclusive: Q quorum for G Þ no Q′ quorum for its negation.
Means q Ç
q′ Î Q~F
for any two quorums. Ex: size >
(n + f )/2
Lifts local exclusion G1 Þ ~G2 to global: Q#G1 Þ ~Q′#G2
Q+: ensures Q even after failures: q+ – zFS Î Q for any q+, zFS
A live quorum has Q+ ≠ {}
Specification
type X = ... values to decide on
var d : (X È {nil}) := nil Decision
input : set X := {}
|
Name |
Guard |
State change |
|
Input(x) |
|
input := input È {x} |
|
Decision: X |
d ≠ nil |
→ret d |
|
|
|
|
|
Decide |
d = nil Ù x Î input |
→d := x |
The Idea of Paxos
A sequence of views; get a decision quorum in one of them.
Each view v chooses an anchored value cv: equals any earlier decision.
If a quorum accepts the choice, decision!
Decision is irrevocable,
may be invisible, but is any later
view’s choice.
Choice
is changeable, must be visible

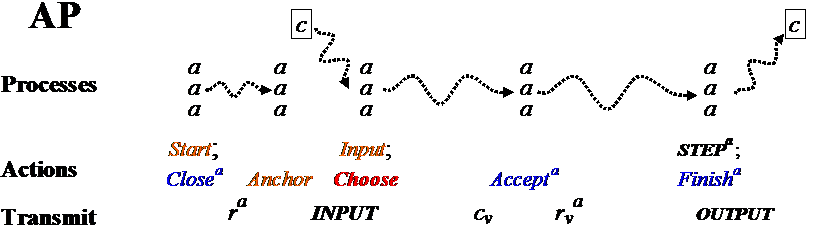
Abstract Paxos—AP: State
Non-local Agents State
functions View is
 rv d
rv d
cv 1: rv1
d 1 Qdec[rv*=x] x x decided
input 2: rv2
d 2
Qout[rv*=out] out nil out
activev 3: rv3
d 3
else nil nil open
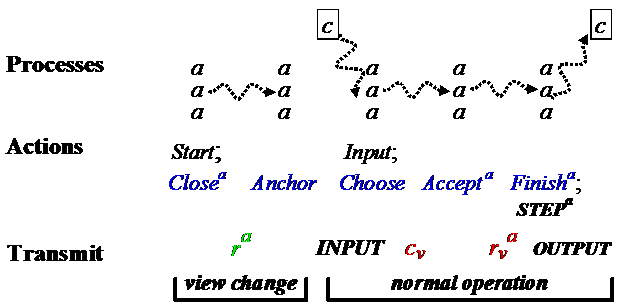
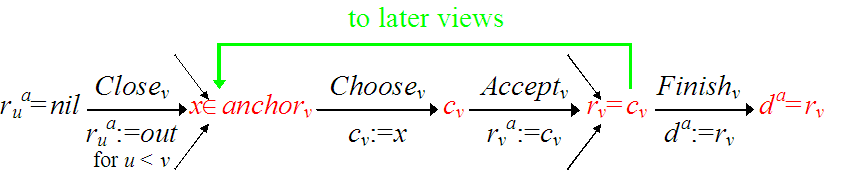
AP: Data Flow
to later views

rua=nil Closev xÎanchorv Choosev cv Acceptv rv=cv Finishv da=rv
rua:=out cv:=x rva:=cv da:=rv
for u < v
Each
value is nil or = the
previous one
Client INPUT x xÎinput
Example
|
|
cv rva rvb
rvc |
cv rva rvb
rvc |
|
View 1 View 2 View 3 |
7 7 out out 8 8 out out 9 out out 9 |
8 8 out out 9 9 out 9 9 out out 9 |
|
input Ç anchor4 |
= {7, 8, 9} seeing a,
b, c |
{9} no matter what |
Two runs of AP with
agents a, b, c,
two agents in a quorum,
input = {7, 8, 9}
Anchoring
|
invariant rv = x Ù ru = x′
Þ x = x′ |
all results agree |
|
|
Ü rv = x Þ (" u < v | cu = x Ú Qout[ru*Î{x,out}]) |
assume u<v rua Î {x, out} Þ ~(rua = x′) |
|
|
sfunc anchorv
|
= |
{x | (" u < v | cu = x Ú Qout[ru*Î{x,out}])} |
|
|
= |
{x | (" w | v0 ≤ w <
u Þ cw = x Ú Qout[rw*Î{x,out}])} |
= anchoru = X if outu,v |
|
= |
{x | cu = x} È (anchoru Ç {x | Qout[ru*Î{x,out}]}) if outu,v |
since |
|
Ê |
if outu,v Ù rua = x then {x} elseif outv0,v then X else {} |
|
where outu,v = (" w | u < w < v Þ rw = out)
AP: Algorithm
|
Startv |
u<v too slow |
→activev := true |
|
|
|
activev |
→for all u < v do |
post u<v Þ rua
≠ nil |
anchorv = {x
| cu = x}
È
(anchoru Ç {x | Qout[ru*Î{x,out}]}) if outu,v
|
Anchorv |
anchorv ≠ {} |
→no state
change |
|
|
Choosev |
cva = nil |
→cv := x |
|
|
Acceptva |
rva =
nil |
→rva := cv; Closeva |
|
|
Finishva |
rv ÎX |
→da := rv |
|
AP: Liveness
 Choose must
see an element of input
Ç anchorv.
Choose must
see an element of input
Ç anchorv.
Recall anchorv
|
= |
{x | cu = x} È (anchoru Ç {x | Qout[ru*Î{x,out}]}) |
|
|
Ê |
if outu,v Ù rua = x then {x} elseif outv0,v then X else {} |
|
After Closeva, an OK agent a has rua ≠ nil for all u < v.
So if Qout is live, we see either u < v is out, or rua = x for some OK a.
But rua = cu Î input Ç anchoru
If we know a is OK, then rua is what we want
With faults (in BP), we might not know. But if anchoru is visible, that is enough.
Optimizations
Fixed-size agent
state:
![]() rwa= don’t know xlasta out nil
rwa= don’t know xlasta out nil
| | |
view v0 vXlasta vlasta
Successive steps:
Because anchorv doesn’t depend on input, can compute it for lots of steps at once.
This is called a view change
One view change is enough for any number of steps
Can batch steps with one Paxos/batch.
Can run steps in parallel, subject to external consistency.
Disk Paxos—DP
The goal—Replace the conditional writes in Close and Accept with simple writes.
|
Acceptva |
rva = nil Ù cv ≠ nil |
→rva := cv; Closeva |
|
The idea—Replace rva with rxva and rova.
|
Acceptva |
cv ≠ nil |
→rxva := cv; Closeva |
|
|
Closeva |
activev |
→for all u < v do
roua:= out |
|
Proof: Keep rva as a history variable. Abstract it to AP’s rva.
This invariant makes it work (sometimes with an extra view).
|
rxva = |
Ù |
rova = |
Þ |
rva |
|
nil |
|
nil |
|
= nil |
|
nil |
|
out |
|
= out |
|
x |
|
nil |
|
= x |
|
x |
|
out |
|
≠ nil |
Communication
A process has knowledge T of stable non-local facts
g@m = (Tm Þ
g)
We transmit these facts (note that transmitter k may be failed):
|
TransmitFk,m(g) |
g@k Ù OKm |
→Tm := Tm Ù (g@k
Ú
Fk) |
post (g@k
Ú
Fk)@m |
A faulty k can transmit anything:
|
TransmitFk,m(g) |
Fk Ù OKm |
→Tm := Tm Ù (g@k
Ú
Fk) |
post (g@k
Ú
Fk)@m |
A fact known to a Q~F+ quorum is henceforth known to a Q~F quorum of OK agents, and therefore eventually known to everyone.
|
Broadcastm(g) |
Q~F+#g Ù OKm |
→Tm := Tm Ù g |
post g@m |
Implement Transmitk,m
by sending messages. It’s fair if k is OK.
This works because the facts are stable.
Classic Paxos—CP
The goal—Tolerate stopped processes
The idea—Agents are the same as in AP. Use a primary process to:
Implement Choose
Compute an estimate rev of rv
Relay facts among the agents
Do all the scheduling.
So the primary sends activev to agents to enable Closev, collects ra, computes anchor, gets inputs, does Choose, sends cp to agents, collects ra again to compute rev, and broadcasts d.
|
Choosep |
activep Ù cp = nil |
→cp := x |
|
Must have only one cp per view. Get this with
At most one primary per view
Primary chooses at most once per view
AP and CP
![]()
![]()
![]()
![]()



Primary: Relay Choose cv Estimate rv
Byzantine Paxos—BP
The goal—Tolerate faulty processes
The idea—To get one cv, a self-exclusive quorum Qch must choose it
Still have a primary to propose cv; an OK agent only chooses this
A faulty primary can stop its view from deciding
Every agent needs
an estimate ceva
of cv and an estimate reva of rv
Invariant: The estimates either are nil or equal the true values.
Every agent also needs its own inputa
|
abstract |
cv =
if |
Qch[cv*=x] |
then
x |
else
nil |
|
|
|
sfunc |
ceva = if |
(Qch[cv*=x])@a
|
then
x |
else
nil |
|
|
|
|
anchorva = |
anchoru Ç {x
| Qout[ru*Î{x,out}]@a} |
if outu,va |
|||
|
|
anchorvp = |
{x | Q~F+[xÎanchorv*]@p} |
|
|||
CP and BP

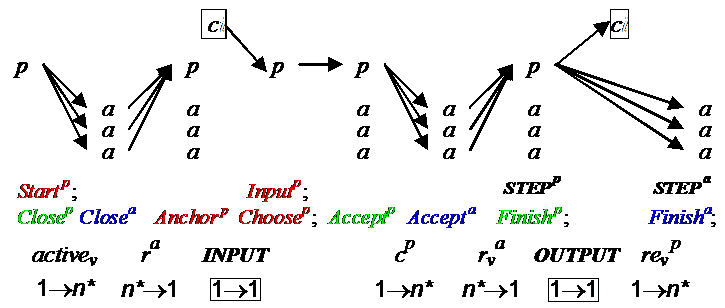


Liveness of BP
 Choose must see an element of input Ç anchorv.
Choose must see an element of input Ç anchorv.
Recall anchorv Ê anchoru Ç {x | Qout[ru*Î{x,out}]}
After Closeva, an OK agent a has rua ≠ nil for all u < v.
So if Qout is live, we see either u < v is out, or rua = x for some OK a.
But rua = cu Î input Ç anchoru
Unfortunately, we don’t know whether a is OK.
But we do have Qch[cu*=x], hence Qch[(x Î anchoru)@a]
So if Qch is live, x Î anchoru is broadcast, which is enough.
So either we eventually see all previous views out, or we see x Î anchoru and all views between u and v out.
A faulty client can wreck a view by not sending input to all agents.
Conclusion
Paxos is a practical protocol for fault-tolerant asynchronous consensus.
Paxos is efficient in replicated state machines, which are the best mechanism for most fault-tolerant systems.
Paxos works in a sequence of views,
Each view chooses a value and then seeks a decision quorum.
A later view chooses any possible earlier decision
Abstract Paxos chooses a consensus value non-locally, and then decides by local actions of the agents.
The agents are read-modify-write memories.
Classic Paxos uses a primary process to choose.
Byzantine Paxos uses a primary to propose, a quorum to choose.