Abstract[1]
We explain how consensus is used to implement replicated state machines, the general mechanism for fault-tolerance. We describe an abstract version of Lamportís Paxos algorithm for asynchronous consensus. Then we derive the Byzantine, classic, and disk versions of Paxos from the abstract one, show how they are related to each other, discuss the safety, liveness, and performance of each one, and give the abstraction functions and invariants for simulation proofs of safety.
Categories and Subject Descriptors
D.2.4 [Software]
Correctness Proofsóabstraction function, invariant, simulation; Fault
ToleranceóByzantine, Paxos, replicated state machine, view change.
[Theory]óconsensus, liveness,
safety.
General Terms
Algorithms, Reliability, Security, Theory
Keywords
Paxos, asynchronous consensus, fault-tolerant, replication, Lamport, Byzantine, state machine
1 Introduction
We give an abstract version AP of Lamportís Paxos algorithm for asynchronous consensus that captures its idea, but is not directly implementable because some of the actions are non-local. Then we give three implementations of AP that solve this problem in different ways, together with the abstractions and invariants of their simulation proofs:
Classic Paxos, CP, from Lamportís original paper [10] and from Liskov and Oki [14], tolerates n/2 stopped processes and requires conditional write (compare and swap) operations on persistent state variables.
Disk Paxos, DP, from Gafni and Lamportís recent paper [6], is a generalization of AP and CP that requires only read and write operations on persistent state variables.
Byzantine Paxos, BP, from Castro and Liskov [1], [2] tolerates n/3 processes with arbitrary faults. Their papers also describe a replicated state machine implementation, based on BP, that has good performance and the same fault tolerance.
AP, CP, and BP are summarized in the appendix.
Iíve tried to answer all the questions I had when I read these papers, about how simple the algorithms can be made, the minimum conditions for them to work, and how they are related. The role that General Λαμπσων played in the original Paxos paper makes it especially appropriate for me to write about a Byzantine version.
I donít know whether a practical algorithm could be developed in this top-down fashion. Certainly the three that we give were not invented in this way, but our exposition does clarify the relationships among them and perhaps will suggest other variations.[2]
1.1 Replicated state machines
The main application for fault-tolerant consensus is replicated state machines. This is the fundamental technique for general fault-tolerance, first described by Lamport [8]. It goes like this:
Cast your problem as a deterministic state machine that takes input requests for state transitions, called steps, from the client, performs the steps, and returns the output to the client. Any computation can be done this way.
Make n copies or Ďreplicasí of the state machine.
Using consensus, feed all the replicas the same input sequence. Then they all generate the same output sequence.
If a replica fails, it can recover by starting in the initial state and replaying all the inputs. Like a transaction system [7], it can speed up this complete replay by starting with a previous state instead of at the beginning.
The steps of the state machine can be arbitrarily complicated as long as they are deterministic, atomic, and strictly local to one replica. To make a big step atomic, use transactions [7]. Of course a replica can involve more than one physical machine; in fact, like any good idea in computer science, the entire method can be applied recursively.
Even reading the state must be done with a step, unless the client is willing to accept output based on an old state. If a read also returns the sequence number of the last step that affected it, the client can pay for better read performance with complexity by doing an occasional step to learn the current step, and then accepting read outputs that are not too far out of date. With a sloppy notion of real time the state machine can give the client a bound on number of seconds a read might be out of date.
Since fault-tolerant consensus makes all the inputs persistent, exactly-once semantics needs no extra persistent writes. The state machine does have to check that an input hasnít been accepted already, which it can do by remembering the most recent input from each client, or just its hash, sequence number, or time-stamp.
The most common application is to data storage systems such as a file system [14]. The method is much more general, however. For instance, state machine actions can be used to change the sets of processes that form the various quorums on which consensus depends, so that no special algorithms are needed to deal with processes that arrive and depart in an orderly way.
Many applications combine a replicated state machine with leases, which are locks on portions of the state. A lease differs from a lock because it times out, so the system doesnít block indefinitely if the leaseholder fails. To keep the lock the holder must renew the lease. There is an obvious tradeoff between the cost of frequent renewals and the cost of waiting for the lease to expire when the leaseholder fails. A client (or a subordinate state machine) with a lease can do arbitrary reads and writes of the leased state without taking any steps of the main state machine, except for a single step that combines all the writes. The most important use of leases is to allow holders to cache part of the state.
Like locks, leases can have different modes such as shared and exclusive, and they can be hierarchical. A parent leaseholder can issue child leases for sub-portions of its state without using consensus; of course the childís lease must expire no later than the parentís.
Consensus is also useful for group membership and transaction commit, if a full replicated state machine is not needed.
1.2 The idea of Paxos
A consensus algorithm decides on one from a set of input values (such as the state machine inputs). It uses a set of processes, called agents in this paper. The simplest form of fault-tolerant consensus decides when a majority of agents choose the same value. This is not very fault-tolerant for two reasons: there may never be a majority, and even when there is, it may remain permanently invisible if some of its agents stop. Since we canít distinguish a stopped agent from a slow one, we canít tell whether the invisible majority will reappear, so we canít ignore it.
To avoid these problems, Paxos uses a sequence of views.[3] A majority in any view decides (or more generally, a decision quorum; see section 4.2), but if a view doesnít work out, a later view can supersede it. This makes the algorithm fault-tolerant, but introduces a new problem: decisions in all views must agree.
The key idea of Paxos is that a later view v need not know that an earlier view decided in order to agree with it. Instead, itís enough to classify each earlier view u into one of two buckets: either it can never decide, in which case we say that itís out, or it has made a choice and it must decide for that choice if it decides at all. In the latter case v just needs to know uís choice.
Thus a view chooses and then decides. The choice can be superseded, but the decision cannot. On the other hand, the choice must be visible unless the view is visibly out, but the decision need not be visible because we can run another view to get a visible decision. This separation between decision and visibility is the heart of the algorithm.
A decision will be unique as long as every later choice agrees with it. We ensure this by anchoring the choice: if all previous views are out, v can choose any input value; if not, it can take the choice of the latest previous view that isnít known to be out. By induction, this ensures that v will agree with any previous decision. To keep the algorithm from blocking, each previous view must be visibly out or have a visible choice. See section 4.3 for a picture of the anchor-choose-decide sequence.
In each view a primary process initiates the choice. A view eventually decides unless the primary fails or a later view starts. A later view may be necessary if the primary fails. Since asynchronous consensus with faults cannot be live [5], there is no reliable way to decide when to start another view. Paxos uses some unreliable way based on timeouts. Thus views may run concurrently.
1.3 Design methodology
Our description of the algorithms is based on a methodology for designing fault-tolerant systems. There are five principles:
Use only stable predicates to communicate state among processes. A predicate is stable if once true, it never becomes false. Hence information about non-local state can never become false. This makes it much easier to reason about the effects of failures and other concurrent actions. We say that a variable is stable if its non-nil value doesnít change: y is stable if (y = constant Ŕ y ≠ nil) is stable. Often variables that are not stable encode stable predicates; see section 4.8 for an example.
Structure the program as a set of separate atomic actions. This simplifies reasoning about failures. If sequencing is necessary, code it into the state; the actions of the primary in CP below are an example of this. This avoids having a program counter and invariants that connect it to the state. State should be either persistent, or local to a sequence of actions that can be abandoned.
Make the actions as non-deterministic as possible, with the weakest possible guards. This allows more implementations, and also makes it clearer why the algorithm works.
Separate safety, liveness, and performance. Start with an algorithm that satisfies a safety property expressed as a state machine specification. Then strengthen the guards on some of the actions to ensure liveness or to schedule the actions; this reduces the number of possible state transitions and therefore cannot affect safety.
Use an abstraction function and a simulation proof to show that an algorithm satisfies its safety specification.[4] Put all the relationships between actions into invariants; it should never be necessary to do an explicit induction on the number of actions. Liveness proofs are more ad hoc.
The top-down development often works by introducing new variables that are related to the abstract variables by an invariant, and modifying the actions so that they depend only on the new variables and not on the abstract ones. The abstract variables thus become history variables in the proof.
1.4 Related work
Classic Paxos was invented independently by Lamport [10] and by Liskov and Oki [14]. This version of Paxos tolerates only stopping faults.
Lamportís work was neglected because of the complicated Paxon fiction he used to describe it. He calls an agent a Ďpriestí and a view a Ďballotí, and describes the application to replicated state machines in detail. A recent extension called Disk Paxos allows read-write memory such as a disk to be used as an agent [6]. My previous exposition of Classic Paxos and state machines calls a view a Ďroundí and a primary a Ďleaderí [13].
Liskov and Okiís work is embedded in an algorithm for data replication, so the fact that they describe a consensus algorithm was overlooked. Not surprisingly, they call an agent a Ďreplicaí; they also use the terms Ďprimaryí and Ďbackupí.
Castro and Liskov introduced Byzantine Paxos, which tolerates arbitrary faults [1][2]. They present it as Liskov and Oki do.
There is an extensive literature on consensus problems, thoroughly surveyed by Lynch [15]. Dwork et al [4] give consensus algorithms that, like Paxos, have a sequence of views (called Ďroundsí) and are guaranteed safe but are live only if views are started prudently. Malkhi and Reiter treat Byzantine quorums [16].
1.5 Organization
Section 2 gives the background: notation, failure model, and quorums. Section 3 is the specification for consensus, followed by AP in section 4 and its DP generalization in section 5. Section 6 explains how we abstract communication, and sections 7 and 8 use this abstraction for CP and BP. Section 9 concludes. An appendix summarizes the notation and the main actions of AP, CP, and BP.
2 Background
2.1 Notation
To avoid a clutter of parentheses, we usually write subscripts and superscripts for function arguments, so g(v, a) becomes gva. We use subscripts for views and superscripts for processes. Other subscripts are part of the name, as in v0 or Qout.
Lower-case letters denote variables and upper-case letters denote sets and predicates (except that q and z denote sets of processes, so that Q and Z can denote sets of sets). A type is a set, but also overloads functions and operators. Names starting with t denote variables of type T.
No-argument functions on the state are Ďstate functionsí, used like variables except that we donít assign to them. Rather than recompute such an r each time itís used, a real program might have a variable r′ and maintain the invariant r = r′.
We use g for a predicate on the state, and G for a process predicate, a function from a process to a predicate. F and S denote specific process predicates; see section 2.2. We lift logical operators to process predicates, writing G1 Ŕ G2 for (λ m | G1m Ŕ G2m).
We write {x ő X | G(x)} in the usual way to describe a set: the elements of X that satisfy G. This extends to {x , y | G(x, y) | f(x, y)} for {z | ($x , y | G(x, y) Ŕ z = f(x, y)}.
The following schema describes actions:
|
Name |
Guard |
††† State change |
|
|
Closev |
cv = nil Ŕ x ő anchorv |
→cv := x |
|
The name of the action is in bold. The guard is a predicate that must be true for the action to happen. The last column describes how the state changes; read ďguard → state changeĒ as ďif guard then state changeĒ. A free variable in an action can take on any value of its type. An action is atomic.
A variable declaration
var†††† y††††††††††† :†† Y := nil††††††††††††††††††††††††††††††††††
gives the variableís name y, type Y, and initial value nil.
When an action or formula derives from a previous version, boxes highlight the parts that change, except for process superscripts. Shading highlights non-local information. Underlines mark the abstract variables in a simulation proof of refinement.
The appendix has a summary of the notation in table 3, and the variables and main actions of the various algorithms in table 4.
2.2 Failure model
We have a set M (for Machine) of processes, and write m or k for a process, and later a or p for an agent or primary process.
We admit faulty processes that can send any messages, and stopped processes that do nothing. A failed process is faulty or stopped; a process that isnít failed is OK. Our model is asynchronous, which means that you canít tell a stopped process from a slow one (after all, both begin with Ďsí). A process that crashes and restarts without losing its state is not stopped, but only slow. A primary process may have a crash or reset action that does lose some state; this is also not a failure.
We define predicates on processes: Fm is true when m is faulty, Sm when m is stopped. These are stable, since a process that fails stays failed. OK = ~(F ŕ S). When a process fails its state stops changing, since failed processes donít do actions. Thus every action at m has Ŕ OKm in its guard, except a send from a faulty process. To reduce clutter we donít write this conjunct explicitly.
A faulty process can send arbitrary messages. For reasoning from the contents of messages to be sound, any g inferred from a message from m must therefore be weaker than Fm, that is, equal to g ŕ Fm. You might think that the state of a faulty process should change arbitrarily, but this is unnecessary. It does all its damage by sending arbitrary messages. Those are its external actions, and they are the same for arbitrary state and for frozen state.
The reason for distinguishing faulty from stopped processes is that faulty processes compromise safety: the system does the wrong thing. Stopped processes can only compromise liveness: the system does nothing. Often safety is much more important than liveness. This is like the distinction in security between integrity and availability (preventing denial of service).
We limit the extent of failures with sets ZF, the set of all sets of processes that can be faulty simultaneously, ZS the same for stopped, and ZFS the same for failed. Clearly ZF Õ ZFS and ZS Õ ZFS.
2.2.1 Examples
The simplest example is bounds f and s on the number of faulty and stopped processes. We define Z≤i = {z | |z| ≤ i}. Then ZF = Z≤f, any set of size ≤ f, and ZS = Z≤s, any set of size ≤ s. If f = 0 there are no faulty processes and only {} is in ZF.
A different example for faults is mutual mistrust. Each process belongs either to Intel or to Microsoft, and both an Intel and a Microsoft process cannot be faulty:
ZF = {z | z Õ zIntel ŕ z Õ zMicrosoft}.
Similarly, for stops we might use geographical separation. All the
processes in
ZS = {zb Õ zBoston, zs Õ zSeattle | |zb| ≤1 ŕ |zs| ≤ 1 | zb » zs}
It seems natural to assume that F ř S, since a faulty process might appear stopped by sending no messages. This implies ZF Õ ZS = ZFS. For the bounded case, it implies f ≤ s. Itís not essential, however, that faulty imply stopped. The important thing about a faulty process is that it can send a false message, which can affect safety, while a stopped process can only affect liveness.
For example, F ř S implies that Intel-Microsoft has no live quorums (see below), since all the Intel processes can be faulty, but if they can all be stopped then none are left to form the Intel part of a quorum. We could, however, configure such a system on the assumption that no more than two processes will stop; then any three processes from each side is a live quorum. This makes sense if each side insists that no decision can depend entirely on the other side, but is willing to wait for a decision if the other side is completely stopped.
2.3 Quorums: Good, exclusive, and live
A quorum set Q is a set of sets of processes. Define Q#G = {m | Gm ŕ Fm} ő Q, that is, G ŕ F holds at every process in some quorum in Q. F is there to make the predicate a sound conclusion from a message. We write Q[rv*=x] for Q#(λ m | rvm = x); here rvm=x stands for any expression.
We require Q to be monotonic (q őQ Ŕ q Õ q′ ř q′ ő Q), so
that making G true at more processes doesnít falsify Q#G. Thus if G is stable, so
is Q#G.
If G1 ř G2 then Q#G1 ř Q#G2.
Itís natural to define Q~F = {q | q Ō ZF}; these are good quorums, with at least one non-faulty process.
Quorum sets Q and Q′
are (mutually) exclusive if we canít have both a Q
quorum for G and a Q′
quorum for its negation: ("G | Q#G ř ~Q′#~G).
This holds if every Q quorum intersects every Q′
quorum in a set of processes that canít all be faulty:
†††† "q ő Q, q′
ő Q′ | q « q′† ő Q~F
This is how we lift local exclusion G1 ř ~G2 to global exclusion Q#G1 ř ~Q′#G2. Exclusion is what we need for
safety.
For liveness we need to relate various quorums to the sets of possibly faulty or stopped processes.
To ensure G holds at some non-faulty process, we need to hear it from a good quorum, one that canít be all faulty, that is, one in Q~F. If g = Gm is independent of m, then Q~F#G ř g; this is how we establish g by hearing from some processes.
To ensure that
henceforth thereís a visible Q quorum satisfying a predicate G, we need a quorum Q+ satisfying G that still leaves a Q quorum after losing any set that can
fail:
†† Q+ = {q′ | ("z ő ZFS | q′ Ė z ő Q}.
If Q+ ≠ {} then Q is live: thereís always some quorum of OK processes in Q.
2.3.1 Examples
The most popular quorum sets are based only on the size of the quorums: Q≥i = {q | |q| ≥ i}. If there are n processes, then for Q≥i and Q≥j to be exclusive, we need i + j > n + f. If ZF = Z≤f then Q~F = Q≥f+1. If ZFS = Z≤s then Q≥i+ = Q≥s+i and Q≥i live requires i ≤ n Ė s, since Q>n = {}. So we get n + f < i + j ≤ 2(n Ė s), or n > f + 2s. Also i > n + f Ė j ≥ n + f Ė (n Ė s), or i > f + s. With the minimum n = f + 2s + 1, f + s < i ≤ f + s + 1, so we must have i = f + s + 1. If s = f, we get the familiar n = 3f + 1 and i = 2f + 1.
With f = 0 there are exclusive Ďgridí quorum sets: arrange the processes in a rectangular grid and take Q to be the rows and Q′ the columns. If Q must exclude itself, take a quorum to be a row and a column, minus the intersection if both have more than two processes. The advantage: a quorum is only √n or 2(√n Ė 1) processes, not n/2. This generalizes to f > 0 because quorums of i rows and j columns intersect in ij processes [16].
For the Intel-Microsoft example, an exclusive quorum must be the union of an exclusive quorum on each of the two sides.
3 The specification for consensus
The external actions are Input, which provides an input value from the client, and Decision, which returns the decision, waiting until there is one.[5] Consensus collects the inputs in the input set, and the internal Decide action picks one from the set.
type†† X††††††† = Ö†††††††††††††††††††††††††††† values to agree on
var†††† d††††††† : (X » {nil})† := nil††††† Decision
††††††††† input† : set X := {}
|
Name |
Guard |
††
State change |
|
|
Input(x) |
|
††† input := input† » {x} |
|
|
Decision: X |
d ≠ nil |
→ret d |
|
|
Decide |
d = nil Ŕ †x ő input |
→d := x |
|
For replicated state machines, the inputs are requests from the clients. Typically there is more than one at a time; those that donít win are carried over to input for the next step.
Itís interesting to observe that there is a simpler spec with identical behavior.[6] It has the same d and Decision, but drops input and Decide, doing the work in Input.
var†††† d††††††††† : (X » {nil})† := nil††† Decision
|
Input(x) |
|
††† if d = nil then optionally d := x |
|
|
Decision: X |
d ≠ nil |
→ret d |
|
A simulation proof that the first spec implements the second, however, requires a prophecy variable or backward simulation.
This spec says nothing about liveness, because there is no live algorithm for asynchronous consensus [5].
4 Abstract Paxos
As we said in section 1.2, the idea of Paxos is to have a sequence of views until one of them forms a quorum that is noticed. So each view has three stages:
Choose an input value that is anchored: guaranteed to be the same as any previous decision.
Try to get a decision quorum of agents to accept the value.
If successful, finish by recording the decision at the agents.
This section describes AP, an abstract version of Paxos. AP canít run on your computers because some of the actions refer to non-local state (marked like this so you can easily see where the implementation must differ). In particular, Choose and cv are completely non-local in AP. Later we will see different ways to implement AP with actions that are entirely local; the key problem is implementing Choose.
AP has external actions with the same names as the spec, of course. They are almost identical to the actions of the spec.
|
Name |
Guard |
†††
State change |
|
|
Input(x) |
|
††† input := input† » {x} |
|
|
Decisiona: X |
da
≠ nil |
→ret da |
|
4.1 State variables
type † V††††††† =† ...†††††††††††††††††††††††††††††††††††† View; totally ordered
††††††††† Y††††††† =† X » {out, nil}
††††††††† A††††††† Õ M = Ö†††††††††††††††††††††††††††† Agent
††††††††† Q†††††† =† set A††††††††††††††††††††††††††††††† Quorum
const Qdec†† :†† set Q := ...†††††††††††††††††††††† decision Quorum set
††††††††† Qout††† :†† set Q := ...†††††††††††††††††††††† out Quorum set
††††††††† v0†††††† :†† V := ...†††††††††††††††††††††††††††† smallest V
The views must be totally ordered, with a first view v0. Qdec and Qout must be exclusive.
var†††† rva††††† :†† Y := nil, but rv0a := out†††† Result
††††††††† da††††† :†† X » {nil} := nil††††††††††††††† Decision
††††††††† cv†††††† :†† X » {nil}† := nil†††††††††††††† Choice
††††††††† input† :†† set X := {}
††††††††† activev††† :†††††††††††††††††††††††††††††††††††††† Bool† := false
Each agent has a decision da, and a result rva for each view; we take rv0a = out for every a. AP doesnít say where the other variables live.
4.2 State functions and invariants
We define a state function rv that is a summary of the rva: the viewís choice if thereís a decision quorum for that among the agents, or out if thereís an out quorum for that, or nil otherwise.
|
sfunc |
rv: Y =††† if |
Qdec[rv*=x] |
then x |
view v decided x |
(A1) |
According to the main idea of Paxos, there should be a decision if thereís a decision quorum in some view. Thus
|
abstract |
d† |
= if rv őX then rv else nil |
|
|
|
|
input |
= input |
|
|
Figure 1 summarizes the state variables and functions.
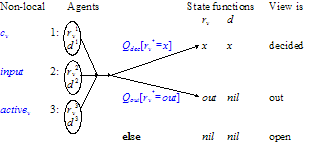
Figure 1: AP state variables and functions
All the variables with short names are stable: rva, da, rv, cv. In addition, activev, x ő input, and x ő anchorv are stable, although the sets are not because they can grow:
input grows in Input;
anchorv is empty until every earlier view is out or has a choice, and then becomes X or that choice; see (A8) below.
AP maintains the following plausible invariants. All but (A3) are summarized in figure 2.
|
invariant |
da ≠ nil ř ($v | rv = da) |
decision is a result |
(A2) |
|
|
rv = x Ŕ ru = x′ ř x = x′ |
all results
agree |
(A3) |
|
|
rva = x ř rva = cv |
agentís
result is viewís cv |
(A4) |
|
|
cv=x ř cv ő input « anchorv |
cv is input and anchored |
(A5) |
|
|
rva ≠ nil Ŕ u < v ř rua ≠ nil |
Close/Acceptv do all u<v |
(A6) |
 Figure 2: AP data flow
Figure 2: AP data flow
Invariant (A3) ensures a unique decision. To see how to maintain it, we rewrite it with some of the universal quantifiers made explicit so that we can push them around:
††††" x′, u |
rv = x Ŕ ru = x′ ř x = x′††††††††††††††††††††††††††††††††††††††††††††††††††††
By symmetry, we can assume u < v. Symbol-pushing and substituting the definition of ru = x′ yields
†† †rv = x ř (" u < v, x′ ≠ x | ~ Qdec[ru*=x′])†††††††††††††††††††††††††††††††† (A7)
How can we exclude Qdec[ru*=x′]? In the scope of x′ ≠ x,
rua ő {x, out} ř ~(rua = x′)
Lifting this exclusion to the exclusive decision and out quorums (see section 2.3), we get Qout[ru*ő{x,out}] ř ~Qdec[ru*=x′]. In addition, cu = x ř ~Qdec[ru*=x′] by (A4), since a decision quorum canít be all faulty. Substituting the stronger predicates, we see that (A7) is implied by
††††rv = x ř† (" u < v | cu = x ŕ Qout[ru*ő{x,out}])††††††††††††††††††††††††††††††
where we drop the quantifier over x′ since x′ no longer appears. You might think that by (A4) Qout[ru*=out] would be just as good as Qout[ru*ő{x,out}], but in fact itís too strong if there are faults, since we can get x from a faulty agent in the quorum even though cu ≠ x.
If we limit rva to values of X that satisfy the right hand side, this will be an invariant. With this in mind, we define
|
sfunc |
anchorv : set X = |
{x | (" u < v | cu = x ŕ Qout[ru*ő{x,out}])} |
(A8) |
This says that x is in anchorv if each view less than v chose x or has an out quorum for (out or x). If all the earlier views are out, anchorv is all of X. If we make cv anchored and set rva only to cv, then (A3) will hold.
Note that this definition does not require every previous view to be decided or out (that would be ... Qdec[ru*=x] ŕ Qout[ru*=out], which is ru ≠ nil). Itís strong enough, however, to ensure that if there is a previous decision it is the only element of anchor, because a decision excludes an out quorum for anything else.
To compute anchor directly from the definition (A8), we need to know a choice or out for each previous view. We can, however,† compute it recursively by splitting the quantifierís domain at u:
††††††††† anchorv
=†††††† {x | (" w | v0 ≤ w < v ř cw = x ŕ Qout[rw*ő{x,out}])}
= ††††††{x |
(" w | v0 ≤ w < u ř cw = x ŕ Qout[rw*ő{x,out}])}
†††† « {x |††††††††††††††††††††††††††††††††† cu† = x ŕ Qout[ru*ő{x,out}]}
†††† « {x |
(" w | u0 < w < v ř cw = x ŕ Qout[rw*ő{x,out}])}
We define outu,v = (" w | u < w < v ř rw = out): all views between u and v are out. If this is true, then the third term is just X, so since cu ő anchoru by (A5):
|
anchorv
= |
{x | cu = x} » (anchoru « {x
| Qout[ru*ő{x,out}]})†† |
(A9) |
If rua = x is the latest visible x, then cu = x by (A4), and the Closev action below makes all views later than u out and ensures that x is in anchorv; note that this x is not necessarily unique. If all the views earlier than v are out, anchorv = X. Thus we have
|
anchorv
|
if outu,v Ŕ rua = x then {x} |
(A10) |
In BP, however, rua may not be visible, so we need the more inclusive (A9) to ensure that Choose can happen; see section 8.3.
4.3 The algorithm
With this machinery the algorithm is straightforward. We Choose an anchored input and then Accept (which canít happen until after Choose, since it needs cv ≠ nil). That leads to a decision, which Finish records for posterity. This is the whole story for safety.
|
Name |
Guard |
††† State change |
|
|
Choosev |
cva = nil Ŕ x ő input « anchorv |
→cv := x |
|
|
Acceptva |
rva = nil Ŕ †cv ≠
nil |
→rva := cv; Closeva |
|
|
Finishva |
rv ő X |
→da †:= rv |
|
For the safety proof, Input and Decisiona simulate Input and Decision in the spec. All the other actions do not change the abstract state and therefore simulate skip in the spec, except for the Accept that forms a decision quorum of agents for cv. This Accept simulates Decide. However, the agent whose Accept simulates Decide has no way of knowing this. In fact, if some agent in the quorum fails before anyone else finds out that it accepted cv, thereís no way for anyone to know that thereís been a decision. There will be another view, and by the magic of anchoring it will choose the value already decided. This can happen repeatedly, until finally thereís a view in which the agents in a decision quorum stay up long enough that others can find out about it; see section 4.4 for an example.
For liveness, however, this is not enough, because Choose needs a non-empty anchor, which we get by doing Close on enough agents to ensure that every previous view either is out or has made a choice. An out quorum is definitely enough. Anchor happens when an out quorum has done Close; it marks the end of a view change (see section 4.9) even though thereís no state change.
|
Startv |
u<v too slow |
→activev := true |
|
|
Closeva |
activev |
→for all u
< v do |
post u<v řrua≠nil |
|
Anchorv |
anchorv ≠{} |
→none |
|
Note that we do not need, and do not necessarily get, ru ≠ nil, since some agents may never close, and even closing all the agents may yield a view thatís neither decided or out.
Agents are just memories; they donít do anything complicated. They cannot be simple read-write memories, however, since they must do the conditional-write or compare-and-swap operations of Close and Accept. Disk Paxos (section 5) implements AP without conditional writes.
With these actions AP finishes provided there are quorums of OK agents and a final view that is the last one in which Close actions occur; see section 4.5 for details.
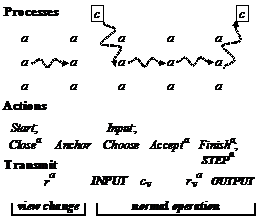
Figure 3: Abstract Paxos
Figure 3 shows the actions of AP for one complete view. It shows communication with vague wavy arrows, since AP abstracts away from that, but the ďtransmitĒ part says what information needs to flow to enable the next action. Capitalized items refer to the state machine application of Paxos: the client (boxed in the figure) provides an input request, the machine takes a step, and it sends the client some output. If there are no faults, any agent could send the output.
4.4 Example
An example may help your intuition about why this works when there are no faults. The table shows views 1-3 in two runs of AP with agents a, b, c, two agents in a quorum, and input† = {7, 8, 9}.
|
† |
cv††††† rva††††† rvb††† rvc |
†cv†††† rva††††† rvb††† rvc |
|
View 1 View 2 View 3††† |
†7††††††† 7†††††††† out††††† out †8††††††† 8†††††††† out††††† out †9††††††† out††††††† out††††† 9† |
† 8†††††† 8†††††† †††out†††† out † 9†††††† 9† ††††††††out†††† 9 † 9†††††† out††††††† out†††† 9 |
|
input Ǡ
anchor4 |
= {7, 8,
9} seeing a, b, c |
†
{9} no matter what |
In the left run all three views are out, so if we compute anchor4 by seeing all three agents, we can choose any input value. If we see only a and b, view 3 appears out but view 2 does not, and hence we must choose 8. If we see only a and c or b and c, view 3 doesnít appear out and hence we must choose 9.
In the right run, view 2 is decided, but we donít see that if either a or c is stopped. Nonetheless, we must choose 9, since we see that value in a non-out view no matter what out quorum we see. Thus a decided view such as 2 acts as a barrier which keeps any later view from choosing another value.
The reason there were three views in both runs is that each view was interrupted by Close in a later one before it had a chance to finish. Otherwise view 1 would have succeeded. If new views keep starting, the algorithm can continue indefinitely.
4.5 Liveness
We want AP to finish in a final view v if thereís no Close action in any later view. It will do so if the actions can see certain things:
∑ Finishv must see a decision d (that is, must see Qdec[rv*=d]). This means that Qdec must be live. Since there are no later views to mess with rva, if Qdec is live Accept will eventually run at enough agents to make d visible. However, d need not be visible in the view that made it. In fact, itís fundamental to Paxos that until Finish has run at a live quorum, you may have to run another view to make d visible. This canít happen in a final view, since it can only happen in u if a later view does Close and sets some rua to out.
∑ Acceptv must see the choice cv, though again perhaps not in every view if processes fail at bad times. This depends on the implementation of cv, which varies. It is trivial with no faults: one process, called a primary, chooses cv and announces it, which works if thereís only one primary for v and it doesnít stop. With faults, BP uses a quorum to get a unique and visible cv, which works if all OK processes choose the same cv and the quorum is live.
∑ Choosev must see at least one element of anchor. Since this doesnít get easier when you run another view, we insist that it be true in every view. This means that every previous view w must become visibly out (Qout[rw*=out] is visible) back to a view u that has a visible choice (A10) or at least is visibly anchored (A9). Hence Qout must be live. Since anchor involves the choice, this also depends on the implementation.
Some element x of anchor that Choosev sees must also be in input. But either anchor = X, in which case input Õ anchor, or x = cu for some u, in which case x őinput by (A5).
If Qout is live, Closev always leads eventually to a visible out quorum of OK agents in every u < v. In this quorum either every agent is out, in which case u is out, or some rua = cu by (A4). So if no faults are allowed, we get a non-empty anchorv immediately from this out quorum by (A10). If there are faults, there may be other out quorums as well, in which we see rua = x ≠ cu if a is faulty. Since we canít tell which out quorum is OK, (A10) isnít enough to anchor v. We need (A9) and some delicate reasoning; see section 8.3.
A view can finish by seeing only an out quorum (for x ő anchorv, which Choose needs) and a decision quorum (for rv = x, which Finish needs). Thus the requirement is Qout and Qdec both live. With no faults and equal size-based quorums, for example, both quorums are the same: more than n/2 agents.
4.6 Scheduling
Doing Close in views later than v may keep Acceptv from happening, by setting too many rva to out before Acceptv has a chance to set them to cv; of course this canít happen in the final view because there are no later views. To get a final view, activev controls the scheduling of Closev. Since asynchronous consensus canít be guaranteed to terminate, there is no foolproof way to do this scheduling.
Schedulers either randomize or estimate the longest time RT for a round-trip from one process to another and back; note that RT includes the time for the processes to run as well as the time for the messages to travel. The idea is that if a view doesnít complete within 2RT, you multicast a new view v. If v is smaller than any other view you hear about within another RT, v becomes active. Obviously this can fail in an asynchronous system, where there is no guarantee that the RT estimate is correct.
Castro and Liskov [1] use the Ethernetís exponential backoff technique to estimate RT; a process backs off whenever it fails to hear from a quorum within its current RT estimate. This works as long as RT does not increase without bound. The estimate can be as much as b times the actual RT, where b is the backoff multiplier, commonly 2. More serious is that if processes stop and then recover, the estimate may be much too large.
Summing this up, with proper scheduling AP finishes as soon as there are Qdec and Qout quorums of processes that havenít failed. We canít implement proper scheduling in general, but itís not hard in most practical situations.
4.7 Cleanup
Once a Q~F+ quorum knows a decision all the other state can be discarded, since no matter what failures occur there will be a good quorum to report d.
|
††† Q~F+[d ≠ nil] |
→for all v do rva := nil; input := {} |
|
4.8 Optimizing agent state
Closeva leaves rua out or cu for all u < v, and by (A10) anchor only depends on the latest view with rua = x. Hence an agent a only needs to keep track of the latest view u for which rua = x and the range (maybe empty) of later views w for which rwa = out. The following variables do this:
vXlasta†††† the latest u for which rua = x (v0 if there is no such u)
xlasta†††††† x (arbitrary if thereís no such u), and
vlasta†††††† the earliest v ≥ u for which rua ≠ out.
For views w between vXlasta and vlasta, rwa = out; for
views past vlasta, rwa = nil.
Thus vXlasta = u ≠ v0 and xlasta = x encode the
predicate rua = x,
and vXlasta = u and vlasta = v encode
†† " w | (u<w<v ř rwa = out) Ŕ (v<w ř rwa = nil) Ŕ (u ≠ v ř rva = nil).
These predicates are stable, although the variables of course are not. Here is the picture.
![]() rwa††††††††††††††††††††† donít know†††††††† xlasta†††††††††† out†††††††††††††††††† nil
rwa††††††††††††††††††††† donít know†††††††† xlasta†††††††††† out†††††††††††††††††† nil
††††††††††††††† |†††††††††††††††††††††††††††††††††††††† |†††††††††††††††††††††††††††† |
view†††††† v0††††††††††††††††††††††††††††††††† vXlasta††††††††††††††††††††† vlasta
This encoding uses space logarithmic rather than linear in the number of views, which makes it cheaper both to store and to transmit the agent state. In practice, of course, we use a fixed amount of space for a view. Close and Accept become
|
Closeva |
activev †Ŕ vlasta < v |
→vlasta := v |
|
Acceptva |
cv ≠ nil Ŕ vlasta = v |
→vXlasta :=
v; xlasta:=
cv; vlasta
:= v |
4.9 Multi-step optimizations
When we use Paxos (or any other consensus algorithm) to implement a replicated state machine, we need to reach consensus on a sequence of values: the first step of the state machine, the second step, etc. By observing that anchorv does not depend on cv, we can compute it in parallel for any number of steps. For most of these, of course, there will have been no previous activity, so the agent states for all the steps can be represented in the same way. We only need to keep track of the last step for which this is not true, and keep separate last triples just for this and any preceding steps that are not decided. To bound this storage, we donít start a step if too many previous steps are not known to be decided.
With this optimization we do Close and compute anchor only when the view changes, and we can use one view for a whole sequence of steps. Each step then requires Choose and Accept to reach a decision, and Finish to tell everyone. Finish can be piggy-backed on the next accept, so this halves the number of messages.
Itís possible to run several steps in parallel. However, in the state machine application the ordering of steps is important: to maintain external consistency a step should not decide an input x that arrives after a later step decided y and sent its output. Otherwise the clients will see that the inputs execute in the order x; y even though they also see that x was not submitted until after y completed; this is generally considered to be bad. To avoid this problem, fill any gaps in the sequence of steps with a special skip step. Of course there shouldnít be nothing but skips.
If there are lots of state machine steps they can be batched, so one run of AP decides on many steps. This is like group commit for transactions [7], with the same tradeoffs: more bandwidth but greater latency, since the client gets no output until a batch runs.
4.10 Other optimizations
An agent can send its rva directly to the client as well as to the other agents, reducing the clientís latency by one message delay. Of course the client must see the same result from a decision quorum of agents; otherwise it retransmits the request. A state machine agent can tentatively do a step and send the output to the client, which again must wait for a decision quorum. In this case the agent must be able to undo the step in case v doesnít reach a decision and a later view decides on a different step. Castro and Liskov call this Ďtentative executioní [1].
If a step is read-only (doesnít change the state of the state machine), an agent can do it immediately and send the client the output. The client still needs a decision quorum, which it may not get if different agents order the read-only step differently with respect to concurrent write steps that affect the read-only result. In this case, the client must try the step again without the read-only optimization.
Itís convenient to describe an algorithm in terms of the persistent variables. In practice we donít keep each one in its own disk block, but instead log all the writes to them in a persistent log. In some applications this log can be combined with the log used for local transactions.
5 Disk Paxos
We would like to implement the agent with memory that has only read and write operations, rather than the conditional writes that AP does in Close and Accept. The main motivation for this is to use commodity disks as agents; hence the name Disk Paxos (DP) [6]. These disks implement block read and write operations, but not the conditional-write operations that AP agents use.
†To this end we add separate state variables rxva and rova in the agent for x and out, and change Close and Accept to unconditionally write out into ro and cv into rx. We want the code to look only at the values of rx and ro, so that rva becomes a history variable, that is, the behavior of the algorithm is unchanged when we remove it.
What makes this work is an invariant that allows us to infer a lot about rva from rxva and rova:
invariant †††††††††††††††††††††††††††††††††††††† relates state to history†††††††† (D1)
|
rxva = |
††Ŕ |
rova = |
ř |
rva |
|
nil |
|
nil |
|
= nil |
|
nil |
|
out |
|
= out |
|
x |
|
nil |
|
= x |
|
x |
|
out |
|
≠ nil |
In particular, if anchor is non-empty we can still always compute at least one of its elements, because the only information lost is some cases in which the view is out, and in those cases we get rva instead, which is enough by (A10). We may miss anchor = X, but we only need a non-empty anchor (and this can happen in AP as well if we donít hear from some agents that are out). We may also sometimes miss a decision because we only know rva ≠ nil when actually rva = x, but this only costs another view (and this too can happen in AP if we donít hear from some agents that accept). In the final view rova = nil and we donít lose any information, so liveness is unaffected.
var†††† rxva†††††† :†† X » {nil} := nil††††††††††††††††††††††††††††††† Result X
††††††††† rova†††††† :†† {out, nil} := nil††††††††††††††††††††††††††††††† Result out
††††††††† rva††††††††† : † Y := nil†††††††††††††††††††††††††††††††††††††††††††† history
|
Closeva |
††† activev |
→for all u
< v do |
post u < v |
|
Choosev |
†† cv = nil |
→cv := x |
|
|
Acceptva |
††† cv
≠ nil |
→rxva := cv; Closeva; |
|
†
|
invariant |
rxva = x ř rxva = cv |
|
(D2) |
With the abstraction rva = rva, DP simulates AP.
A more general version encompasses both AP and DP, by allowing either a conditional or an unconditional write in Close and Accept. It replaces the boxed sections with the following:
Closeva†† Ö if rxua = nil, or optionally anyway, roua := out
Acceptva Ö if roua = nil, or optionally anyway, rxva := cv
Liveness and scheduling are the same as for AP. The last-triple optimization needs special handling; it is discussed in section 7.2.
6 Communication
For the algorithm to progress, the processes must communicate. We abstract away from messages by adding to mís state a stable predicate Tm called its Ďtruthí that includes everything m knows to be true from others; T also stands for Ďtransmittedí. If g is a stable predicate, we write g@m for Tm ř g, and read it ďm knows gĒ or ďm sees gĒ or ďg is visible at mĒ. The safety invariant is
|
invariant |
g@m
ř g |
|
(T1) |
In other words, everything a process knows is actually true. This invariant allows us to replace a non-local guard g in an action at m with the stronger local g@m. The resulting code makes fewer transitions and therefore satisfies all the safety properties of the original, non-local code. Liveness may be a challenge.
We lift @ to process predicates: G@m = (λ k | Gk@m). Then (Q#G)@m = Q#(G@m): seeing G from a quorum is the same as seeing a quorum for G. Read Q[g@*] as ďa Q quorum knows gĒ, where g is a predicate, not a function from processes to predicates.
Note that m canít communicate g@m if m might be faulty. This is not an issue when we use g@m in a guard at m, but we can only get (g@m ŕ Fm)@k rather than (g@m)@k.
6.1 Messages
The implementation, of course, is that g@m becomes true when m receives a message from k asserting g; recall that g is stable and therefore cannot become false if k fails. We model the message channel as a set ch of terms gk→m (read ďg from k to mĒ). Here are all the actions that affect ch or T:
|
Name |
Guard |
††† State change |
|
|
Localk(g) |
g |
→Tk :=
Tk Ŕ (g ŕ Fk) |
post
(g ŕ Fk)@k |
|
Sendk,m(g) |
g@k † |
→ch := ch » {gk→m} |
post gk→m ő ch |
|
SendFk,m(g) |
Fk†† |
→ch := ch » {gk→m} |
post gk→m ő ch |
|
Receivem(g) |
gk→m ő ch |
→Tm
:= Tm Ŕ (g@k ŕ Fk) |
post(g@k ŕ Fk)@m |
|
Drop(g) |
gk→m ő ch |
→ch := ch - {gk→m} |
|
So k can use Local to add to Tk any true predicate g; presumably g will only mention kís local state, since otherwise it would be in Tk already.[7] Then k can send gk→m to any process m if either k knows g or k is faulty. We separate the two send actions because SendF is not fair: thereís no guarantee that a faulty process will send any messages.
|
invariant |
gk→m ő ch ř g@k ŕ Fk |
|
(T2) |
|
|
(g@k ŕ Fk)@m ř g@k ŕ Fk |
|
(T3) |
From the two send actions we have (T2) since g is stable and therefore g@k ŕ Fk is stable. Receivem(g) adds g@k ŕ Fk to mís truth. Since this is the only way to establish (g@k ŕ Fk)@m, (T3) follows from (T2). (T1) follows from this and Local, since they are the only ways to establish g@m.
These actions express our assumption that the only way m can receive g from a non-faulty k is for g to be true. In other words, thereís no way to fake the source of a message. Usually we get this security either by trusting the source address of a message or by cryptographic message authentication; see [1] for details of how this works for BP.
6.2 Transmit
We now abstract away from the channel to actions that establish g@m directly:
k can transmit g@k to all the other OK processes, even if k fails. This allows for messages that remain in ch after k fails.
A faulty k can transmit anything.
|
TransmitFk,m(g) |
g@k Ŕ OKm |
→Tm := Tm Ŕ (g@k ŕ Fk) |
post (g@k ŕ Fk)@m |
|
TransmitFk,m(g) |
Fk†† †Ŕ OKm |
→Tm := Tm Ŕ (g@k ŕ Fk) |
post (g@k ŕ Fk)@m |
We say that m hears g@k ŕ Fk from k. When thereís a quorum Q#G@m, we say that m hears G from a Q quorum. In the simulation proof Receivem(g) of gk→m simulates Transmitk,m(g) by (T2) because g@k is stable, and the Send actions simulate skip.
As before, both Transmitk.m and Broadcastk,m (see below) are fair if k is OK, and so is Broadcastm, but TransmitF is not. This means that if g@k holds, and OKk and OKm continue to hold, then eventually (g@k ŕ Fk)@m or g@m will hold.
A history variable can appear in a predicate g in Tk, even though it canít appear directly in a guard or in an expression assigned to an ordinary variable, since itís not supposed to affect the actions that occur. Such a g can get into Tk initially if an invariant (such as (C1)) says itís implied by a g′ that doesnít contain a history variable. Once itís in Tk, g can be transmitted in the usual way. This is just a way of encoding ďg′ was true at some time in the pastĒ. So if g′ has no history variables, and g and g′ ř g are stable:
|
Localk(g) |
g′ Ŕ (g′ ř g) |
→Tk := Tk Ŕ (g ŕ Fk) |
post g@k ŕ Fk |
The Local, Transmit, and Broadcast actions are the only ones we need for the rest of the paper.
6.3 Broadcast
If a Q~F+ quorum
ever knows g, then henceforth thereís always a Q~F quorum of OK processes that knows g. Hence
repeated Transmits
will establish (Q~F[g@*])@m
at every OK process m. But Q~F[g@*] ř g,
so this establishes g@m. We package
this in an action:
|
Broadcastm(g) |
Q~F+[g@*] Ŕ OKm |
→Tm := Tm Ŕ g |
post g@m |
If we have broadcast messages (signed by public keys) thereís a more direct way to broadcast a predicate. We can drop the m from gk→m, since any process can read the messages.[8] This means that if Receivek establishes g@k, then g@m follows too, not simply (g@k ŕ Fk)@m. In other words, k can transmit a transmitted g@k without weakening it, by simply forwarding the messages that k received. If g@k follows from Localk, g@k = (g@k ŕ Fk). Thus, provided k remembers the signed evidence for g, it can do
|
Broadcastk,m(g) |
g@k †††††††††††Ŕ OKm |
→Tm := Tm Ŕ g |
post g@m |
6.4 Implementation and scheduling
We transmit predicates, but since they take only a few forms, an implementation encodes a predicate as a message with a kind field that says what kind of predicate it is, plus one field for each part of the predicate that varies. For example, after doing Closeva agent a sends (closed-state, a, last-triplea).
The Send actions that implement Transmit need to be scheduled to provide congestion and flow control, any necessary retransmission, and prudent use of network resources. How this is done depends on the properties of the message channel. For example, TCP is a standard way to do it for unicast on an IP network. For a multicast such as Broadcast, scheduling may be more complex.
Since processes can fail, you may have to retransmit a message even after a quorum has acknowledged its delivery.
7 Classic Paxos
To turn AP into an implementation, we can take APís agent almost as is, since the agentís Close, Accept, and Finish actions only touch its local state rva. We need to implement input, activev, and cv, which are the non-local variables of AP, and the Input, Start, and Choose actions that set them. We also need to tell the agents that they should invoke their actions, and give them activev and cv. Our first implementation, CP, tolerates stopped processes but no faults.
Since CP is a real implementation, the actions refer only to local state. We still use shading, but now it marks state in T transmitted from other processes. We discuss the scheduling of these Transmit actions in section 7.1. Look at Table 4 to see how non-local information in AP becomes either local state or transmitted information in CP and BP.
CP implements AP by doing Input, Start, and Choose in a primary process. For fault tolerance there can be several primaries. However, for each view there is exactly one process that can be its primary; in other words, there is a function p(v) that maps each view to its primary. If in addition a primary never reuses a view for which it has already chosen a value, there is at most one cv for each v. A simple implementation of pv is to represent a view by a pair, with the name of its primary as the least significant part.
An agentís state must be persistent, but we allow a primary to reset, lose its state, and restart in a fixed state. Then it starts working on a new view, one for which it never chose a result before. We discuss later how to find such a view.
The primaryís job is to coax the agents to a decision, by telling them when to close, choosing cv, and relaying information among them. Once it has a new view, the primaryís Choose action chooses an anchored value cv for the view. To do this it must collect enough information from the agents to compute a non-empty subset of anchorv. (A10) tells us how much information suffices: either that all previous views are out, or that all views since u are out and cu. So itís enough to trigger Closeva at an out quorum (with Closep) and then collect the state from that quorum.
Once the primary has cv, it can try (with Acceptp) to get the agents to accept it. They respond with their state, and if the primary sees a decision quorum for cv, then there is a decision which the primary can tell all the agents about (with Finishp).
We fearlessly overload variable names, so we have cv and cp, for example, and v and vp.
The agent variables of AP become agent variables of CP.
var†††† rva††††††††† :†† Y := nil, but rv0a := out†††††† Result
††††††††† da††††††††† :†† X » {nil} := nil††††††††††††††††† Decision
All the other variables of AP become primary variables of CP, except that activep is coded by vp:
type † P††††††††††† Õ M = Ö†††††††††††††††††††††††††††††† Primary
var†††† vp†††††††††† :†† V := v0†††††††††††††††††††††††††††††† Primaryís View
††††††††† cp†††††††††† :†† X » {nil} :=
nil††††††††††††††††† Primaryís Choice
††††††††† inputp†††† :†† set X := {}
|
sfunc |
activep = |
† (vp ≠ v0) |
|
These are not stable across resets, so we add history variables that are, with the obvious invariants relating them to cp and activep.
var†††† cv†††††††††† :†† X » {nil} := nil †††††††††††††††† history
††††††††† input††††† :†† set X :=
{}†††††††††††††††††††††††† history
††††††††† activev††† :†† Bool† := false†††††††††††††††††††† history
|
invariant |
activep
Ŕ cp ≠ nil ř cp = cvp |
|
(C1) |
|
|
inputp Õ input |
|
|
|
|
activep ≠ nil ř activep = activevp |
|
(C2) |
Thus all the variables of AP are also variables of CP with the identity abstraction function to AP. The invariants (A2-A6) of AP are also invariants of CP.
Any primary can accept an input. For a state machine, this means that any primary can receive requests from clients. The client might have to do Inputp at several primaries if some fail.
|
Inputp(x) |
|
inputp := inputp » {x}; input := input » {x} |
|
We define the primaryís estimates of rv and anchorv in the obvious way. We define revp rather than just rep because p needs views earlier than vp to compute anchor. From (A1) for rv:
|
sfunc |
revp
=†††† if |
(Qdec[rv*=x]†† )@p |
then x |
view v decided x |
(C3) |
From (A10) for anchor:
|
|
outu,vp = |
("w |
u < w < v ř rewp
= out) |
|
|
sfunc |
anchorp |
if††††† †outu,vp Ŕ (rua = x)@p then {x} |
(C4) |
Two unsurprising invariants characterize the estimates:
|
invariant |
revp ≠ nil ř revp = rv |
|
(C5) |
|
|
anchorp Õ anchorvp |
|
(C6) |
We avoid a program counter variable by using the variables vp and cp to keep track of what the primary is doing:
|
vp |
cp |
pís view
of agent state |
Action |
|
= v0 |
- |
- |
Startp |
|
≠ v0 |
= nil |
anchorp = {} |
Closep |
|
≠ v0 |
= nil |
anchorp ≠
{} |
Choosep |
|
≠ v0 |
≠ nil |
revpp Ō X |
Acceptp |
|
≠ v0 |
≠ nil |
revpp ő X |
Finishp |
To keep cvp stable we need to know cvp = nil before setting it. The following invariant lets us establish this from local state:
|
invariant |
activep
Ŕ cp = nil ř cvp = nil |
|
(C7) |
To maintain this invariant we put a suitable guard on the Startp action that makes p active. This is an abstract action since it involves cv; section 7.3 discusses how to implement it.
|
Startvp |
††† u < v
too slow |
→ activev :=
true; vp := v; cp := nil |
|
With this machinery, we can define Choosep as a copy of APís Choosev, with activep added to the guard and the primaryís versions of c, input, and anchor replacing the truth. (C3) and (C7) ensure that Choosevís guard is not weakened.
|
Choosep |
††† activep Ŕ cp = nil |
→cp := x; cvp := x |
|
The agentís actions are the same as in AP (see section 4.3) with cv@a and revp@a for cv and rv. With these actions itís easy to show that CP simulates AP, using (A2-A6) and (C5-C6).
We can use the last optimization in CP just as in AP, and of course the view change optimization works the same way.
7.1 Communicating with agents
As we saw above, the definitions of revp and anchorp imply that the agents tell the primary their state after Closea and Accepta. In addition, the primary tells the agents when to close, and what values to use for accept and finish. It implements these actions by sending trigger messages to the agents, using the invariants shown; since we are abstracting away from messages, we describe them informally. The agents respond by returning their state.
|
Closep |
activep Ŕ cp = nil |
→trigger Closeva at
all agents, send- |
|
Anchorp |
anchorp ≠ {} |
→none |
|
Acceptp |
cp ≠ nil Ŕ revpp = nil |
→trigger Acceptva at
all agents, |
|
Finishp |
revpp ő X |
→trigger Finishva at all agents, |

Figure 4: Classic Paxos
Figure 4 shows the actions of CP for one complete view, with n = 3 agents; compare figure 3. The arrows show the flow of messages, and the ďtransmitĒ part shows their contents and whether they are unicast or multicast. An n* means that if the primary is also an agent, only n Ė 1 messages need to flow. To finish, of course, only a quorum of agents is needed, and only the corresponding messages. In normal operation, however, when no processes are stopped, itís desirable to keep all n of them up to date, so they should all get at least the Finish message.
Liveness, scheduling, and cleanup are the same as APís. A primary can discard all its state at any time with Reset (section 7.3).
In practice the primary is usually one of the agents, and only two other agents are needed to tolerate one stopped process. Itís also possible to compute only at the primary and use the agents just to store the state of the state machine; in this case the Finish message contains the state changes instead of d.
7.2 Implementing DP
Implementing DP with CP is completely straightforward except for the log-space representation of the agent state. We canít just use the triple of last values, because if a primary overwrites one of those unconditionally with an earlier view, it will change some rva back to nil. Instead, we keep a triple for each primary, so the state of an agent is the last triple as in AP, but each component is a function from p to a value (implemented, of course, as an array indexed by p). Then the primary rather than the agents can enforce the guards on writing the agent state, since each variable has only one writer. We abstract vXlast and vlast as the maximum over the primaries, and xlast as the value that goes with vXlast. Reading an agentís state thus requires reading the triples for all the primaries.
This read operation is not atomic, however, so these abstractions are not enough to show that DP-last implements AP-last. Fortunately, they donít need to be, since what we care about is implementing DP. For this we donít need the last values but only enough information about rxua and rxua to do the actions. As we saw in section 4.8, each lastpa triple encodes two predicates on ra, and all of them together encode the conjunction of the predicates. Thus setting vXlast,pa := u and xlast,pa := x is equivalent to setting rxua := x, and setting xlast,pa := u and vlast,pa := v is equivalent to setting rowa := out for all w between u and v. (In addition, some information about earlier values of rxa and roa may be lost, but nothing is changed.) Thereís never a contradiction in these predicates, because cv is the only value we write into rxva. By reading all the triples, we get a predicate that implies the facts about rxa and roa that would follow from:
|
|
vXlasta |
= max over p
of vXlast,pa |
|
|
|
xlasta † |
= xlast,pa for the p
for which vXlast,pa = vXlasta |
|
|
|
vlasta † |
= max over p of vlast,pa |
|
It follows that DP-last implements DP.
A primary p can write all three values at once provided it finds suitable values vXlast,p and xlast,p to write into vXlast,pa and xlast,pa in Close. This is useful because it allows a to keep the whole triple in a single disk block. The values already there are suitable; so are those that accompany the largest vlast,pa in an out quorum.
Precisely, we have:
|
Closev,pa |
|
††† vlast,pa :=
v; |
|
|
Acceptv,pa |
cv ≠ nil |
→vlast,pa := v; vXlast,pa := v; vXlast,pa := cv |
|
7.3 Finding a new view
If the primary has a little persistent state, for example a clock, it can use that to implement Startp, by choosing (clock, p) as a v that it has never used before, which ensures cv = nil.
To get by without any persistent state at the primary, Startp queries the agents and chooses a view later than some view in which a decision quorum of agents is not closed.
|
Resetp |
|
††† †vp
:= v0; inputp :=
{}; cp :=
nil |
|
Startvp |
††† u < v
too slow |
→vp := v; activevp:= true |
This works because before choosing a result, a primary closes an out quorum at all previous views, and the two quorums must intersect. The invariants we need are (A6) and
|
invariant |
Qdec[ru*=nil] Ŕ
v > u ř† cv = nil |
|
(C8) |
This argument is trickier than it looks, since Qdec[ru*=nil] is not stable. The true, stable condition is ďat some time after the primary reset, a decision quorum of agents was still openĒ. Then p can conclude cv = nil if pv = p, since only p can change cv. To establish this condition, the query must not get a reply that was generated before the reset. We can ensure this if thereís a known upper bound on how long the reply can take to arrive (which is true for SCSI disks, for example), or with standard techniques for at-most-once messages on channels with unbounded delays. Unfortunately, the latter require some persistent state in the primary, which is what we are trying to avoid. We wonít formalize this argument.
If the primary sees any agent out in vp or sees any non-nil agent variable for a bigger view u, it restarts, since this means that a later view has superseded the current one. To restart, p chooses one of its views that is bigger than any it has seen to be out. This is another implementation of the abstract Startp, more efficient when the primaryís state hasnít been lost.
|
Restartvp |
††† activep Ŕ vp<u<v Ŕ pv = p |
→vp:= v; cp := nil |
|
7.4 Performance
As figure 4 shows, a normal run of CP that doesnít need a view change multicasts two messages from the primary to the agents, and each agent sends one reply. The output to the client can go in parallel with the second multicast, so that the clientís latency is one client-primary round-trip plus one primary-agents round trip. Usually the finish message piggybacks on the accept message for the next step, so its cost is negligible. Cleanup takes another (piggybacked) agents-primary-agents round trip. See table 1 in section 8.7. With tentative execution (section 4.10) the primary-agents round-trip is reduced to one way.
A view change adds another primary-agents round trip, and if the primary has to run Start, there is a third one. The last only happens when the primary crashes, however, in which case this cost is probably small compared to others.
For a more detailed analysis see [3].
8 Byzantine Paxos
BP is a different implementation of AP, due to Castro and Liskov [1], that tolerates arbitrary faults in ZF of the agents. Their description interweaves the consensus algorithm and the state machine, assumes the primary is also an agent, and distinguishes it from other agents (called Ďbackupsí) much more than we do here. They use different names than ours; see table 2 in the appendix for a translation.
With faults it is unattractive to have separate primary processes for Choose or for relaying information among the agents, so we do Choose in the agents and use multicast for communication among them. Thus BP starts with AP, keeps all the agent variables rva and da, and adds agent versions of the other variables, and a history variable for input as in CP.
const Qch†††††††† :†† set Q := Ö†††††††††††††††††††††† choice Quorum set
var†††† rva††††††††† :†† Y := nil, except rv0a := out††††††† Result
††††††††† da††††††††† :†† X » {nil} := nil††††††††††††††† Decision
††††††††† cva††††††††† :†† X » {nil} := nil††††††††††††††† Choice
††††††††† inputa†††††† :†† set X
:= {}
††††††††† input††††† :†† set X := {}†††††††††††††††††††††† history
††††††††† activeva† :†† Bool† := false
Thus all the variables of AP are also variables of BP with the identity abstraction function, except for cv. The abstraction to cv is a choice quorum of the agentsí choices.
|
abstract |
cv |
= if
Qch[cv*=x] then x else
nil |
|
Agent a adds a value to inputa when a client transmits it; we donít formalize this transmission. Since clients can also fail, other agents may not see this value.
|
Inputa(x) |
|
††† inputa :=
inputa »{x}; input := input »{x} |
|
Thereís still only one choice cv for a view, however, because Qch excludes itself, and the quorum must agree that the input came from the client. Thus any decision is still for a client input and still unique no matter how many faulty clients there are. For the effect of faulty clients on liveness, see the end of section 8.3.
We define ceva as aís estimate of cv, like cv except for the ď@aĒ:
|
sfunc |
ceva = if |
†(Qch[cv*=x])@a |
then
x |
aís estimate of cv |
(B1) |
Similarly, a quorum of rvas makes a result (as in AP), and reva is aís estimate of that result, the same as CPís revp:
|
sfunc |
reva = if |
(Qdec[rv*=x] †††)@a |
then
x |
view v
decided x |
(B2) |
The state function rv is defined in AP; itís (B2) without the ď@aĒ.
With these definitions, the agentsí non-nil estimates of r and c agree with the abstract ones, because they are all stable and (A4) means we see at most one rva from the OK agents. These invariants are parallel to (C1) and (C5):
|
invariant |
ceva ≠ nil
ř
ceva = cv |
c estimates
agree |
(B3) |
|
|
reva †≠ nil ř reva †= rv |
r estimates agree |
(B4) |
We take APís anchorv as a state function of BP also. Following (A9) with reva for rv and without the cu term, we define:
|
|
outu,va = |
("w | u
< w < v †ř rewa = out) |
|
|
sfunc |
anchorva
= |
anchoru « {x | Qout[ru*ő{x,out}]@a} if outu,va |
(B5) |
The missing a on anchoru is not a misprint. We have the obvious
|
invariant |
anchorva Õ anchorv |
|
(B6) |
There is still a role for a primary, however: to propose a choice to the agents. This is essential for liveness, since if the agents canít get a quorum for some choice, the view canít proceed. BP is thus roughly a merger of APís agents and CPís primary. As in CP, the primary is usually an agent too, but we describe it separately.
Safety cannot depend on the primary, since it may be faulty and propose different choices to different agents. If thereís no quorum for any choice, the view never does Accept and BP advances to the next view as discussed in section 8.4.
The primary has a persistent stable cvp (but see section 8.8 for an optimization that gets rid of this). The primary needs inputp in order to choose, but it doesnít need vp since it just works on the last anchored view.
var†††† cvp††††††††† :†† X » {nil} := nil††††††††††††††††† Primaryís
Choice
††††††††† inputp†††† :†† set X
:= {}
An annoying complication is that when the primary chooses cvp, it needs to be able to broadcast cvp ő anchorv so that all the agents will go along with it. To broadcast, p needs Q~F+[(cvp ő anchorv)@*] (see the discussion of broadcast at the end of section 6), so a value thatís anchored at the primary had better be anchored at enough agents, because anchorva is their only approximation of anchorv. Then
|
sfunc |
anchorvp |
= {x | Q~F+[xőanchorv*]@p} |
(B7) |
Thus to compute anchorvp, p needs to hear from Q~F+ agents.
8.1 The algorithm
The agentsí actions are essentially the same as in AP; (B3-B4) imply that the guards are stronger and the state change is the same.
|
Closeva |
activeva |
→for all u < v do |
|
|
Anchorva |
anchorva ≠ {} |
†††
none |
|
|
Acceptva |
†ceva
≠ nil Ŕ† rva
= nil |
→rva := ceva;
Closeva |
|
|
Finishva |
†reva őX |
→da †:= reva |
|
The primary does Input and Anchor as in CP, though the definition of anchorvp is quite different.
|
Inputp(x) |
|
†† †inputp := inputp »{x} |
|
|
Anchorvp |
anchorvp ≠ {} |
→none |
|
Choose is like APís Choose, but at both agents and primary:
The primary chooses for a view that belongs to it and is anchored, but where it hasnít chosen already.
An agent only chooses the primaryís apparent choice.
(B5)-(B6) mean that the agentsí guards are stronger than in AP; this is what matters, since cva is whatís in the abstraction to cv.
|
Choosevp |
††† pv = p Ŕ cvp = nil |
→cvp := x |
|
|
Chooseva |
††† cva = nil |
→cva := x |
†† |
Thereís no guarantee that cvp is in input, but this wouldnít be strong enough anyway, since for liveness it must be in inputa for a choice quorum.
|
invariant |
cvp ≠ nil ř cvp ő inputp « anchorvp |
|
(B8) |
|
|
cva ≠ nil ř cva ő input « anchorva |
|
(B9) |
A client must hear da from a good quorum of agents.
For safety, in
addition to APís assumption that Qdec and Qout are exclusive, Qch must exclude itself. Then the
invariants (A2-A6) of AP hold in BP, and the Closea, Accepta,
and Finisha
actions of BP simulate the same actions in AP. All the other actions simulate skip except the Choosea action that forms a
quorum, which simulates APís Choose.

Figure 5: Byzantine
Paxos
Figure 5 shows the flow of messages in BP. This is the logical flow. If the client-agents network is much slower than the inter-agent network, which is common in practice, the client can send an input just to the primary, including message authenticators for all the agents; the primary forwards the input to the agents. This does not change any costs or affect cryptographic authentication of messages. It does mean that the client may have to resend to another primary if the first one turns out to be faulty.
8.2 Communicating with agents
In BP the primaryís only job is to propose cvp to the agents, who are responsible for everything else including scheduling, since they canít count on the possibly faulty primary. So Transmit and Broadcast are all there is to say about communication.
8.3 Liveness
We want to show that a view with an OK primary will produce a decision unless a later view starts. We assume that Qdec, Qout, and Qch are live, and Qch Õ Q~F+; if these donít hold BP is still safe, but it may not decide. Suppose initially that anchorva anchorvp ≠ {} at a choice quorum of OK agents; this is the case after a view change. Then we have normal operation, which is the easy part of the liveness argument. If the clients are OK:
Since anchorvp ≠ {}, an OK primary can do Choosevp, which leads to cvp@a at all the agents, so that they can all do Chooseva by (B7) provided cvp ő inputa, that is, a knows the client really sent cvp. An OK client will send its input to all the agents, but a faulty client may fail to do so.
This leads to an OK choice quorum for cvp because Qch is live, which leads to knowing that quorum at all the agents so that they can all do Accepta.
This leads to an OK decision quorum for rva = cvp because Qdec is live, which leads to knowing that quorum at all the agents, so that they can all do Finisha.
This leads to knowing a good quorum for da = cvp (or alternatively for the output) at the client, because Q~F is live.
Now we consider what happens in a view change. For an OK agent a to get anchorva ≠ {}, it needs x ő anchorua and Qout[ru*ő{x,out}]@a for some u < v, and rewa = out for each u < w < v, from (B5). This is the tricky part, since these require quorums, and having a quorum is no guarantee that itís visible.
Since Qout is live, thereís an out quorum q of OK agents that will eventually do Closev. Hence eventually Qout[rw*ő{cw,out}]@a for each w < v, since this is the post-condition of Close. Either all these views are out at a, or thereís some largest u < v and a′ ő q with rua′ = cu ≠ nil. In the former case anchorv = X. In the latter case Qch[cu*=x], and hence Qch[(x ő anchoru)@*] by (A5) and (B6). Hence x ő anchoru is broadcast since Qch Õ Q~F+, so eventually we have (x ő anchoru)@a, as required.
This argument is more subtle than it looks. Note that a doesnít know which of the out quorums it sees come from OK agents, so it doesnít know x = cu, and in fact cu might be nil.
To sum up, since a eventually hears from a Qout of OK agents, it hears, for some view u and each w between u and v,
an out quorum for w and
Qout[ru*ő{x,out}]@a and (x ő anchoru)@a,
and this is all a needs to anchor v, by (B5).
All that remains is the liveness of Anchorvp: the primary must see a non-empty intersection of anchorva sets from a Q~F+ quorum. Since such a quorum is live, eventually every agent in it will hear from the same q of OK agents and come up with the same x ő anchorv, which will thus be broadcast.
So BP is live, except for faulty clients, although itís hanging on by its fingernails.
If the client is faulty, it can fail to deliver inputs to some agents. A view change that has x = cu ≠ nil and broadcasts x ő anchoru can broadcast x ő input as well and override the clientís failings. This is essential, since there might be a decision for x. During normal operation, however, a faulty client can cause a view change if the primary chooses an input that the client did not send to Qch OK agents.
Agents can keep track of such clients and refuse to accept more input from them. If there are lots of them mounting a denial of service attack, however, performance can still be significantly affected. I donít know any way to prevent this except for the primary to insist that each input be broadcast by getting an ack from Q~F+ agents, or by public key as in section 8.6. This is expensive, since it happens in normal operation, not just in a view change.
8.4 Scheduling
A faulty primary cannot keep BP from satisfying its safety spec, but it can certainly prevent progress. We therefore need a way to ensure that there are times when thereís only a non-faulty primary. To do this, we let the agents become primary in round-robin order. That is, we use integers as views and take a viewís primary to be the view modulo n: pv = v mod n.
An agent a keeps an estimate PT of the time to process a client input. If a gets input from a client at time t and doesnít see some decision by t + PT, a assumes that the primary has failed. It advances to the next view v, does Closeva, and multicasts its state in a Closev message. Other agentsí timers expire, they do the same thing, and when a sees enough Closev messages it does Anchorva and sends its anchorva set to the new primary pv; see section 8.3.
|
Startva |
††† vĖ1 too
slow ŕ Q~F[activev*]@a |
→activeva := true |
If a gets Closeu messages for various u > v from a good quorum, it changes its v to the smallest u and does Closeu. Thus the OK agents increase v at most n times before they agree on the next view, and faulty agents canít disrupt this agreement. This is not quite the same as self-stabilization, since it relies on not running out of values for v.
BP uses the same exponential backoff as AP to adjust PT.
8.5 Cleanup
This is similar to AP, but there is a lot more agent state. As in CP, the primary can discard its state at any time, and the extra transmits for Cleanup can be piggy-backed on the next step.
|
Cleanupa |
††† Q~F+[d
* ≠ nil] |
→ rva := nil; ina := {}; |
|
8.6 Public key BP
As we saw in section 6, if messages can be broadcast securely, that is, signed by public keys, then a process can forward information to other processes so that they donít have to get it from the source. This does not add any new power, but it avoids the Q~F+ acknowledgements otherwise needed for a broadcast.
There are two points where BP needs a broadcast, of inputa in normal operation and of anchora in a view change:
1. The primary can broadcast an input to all the agents, so a faulty client cannot force a view change.
2. During a view change the Anchorvp action is not needed. That is, an agent does not need to acknowledge x ő anchorva to the primary, since the information on which anchorva is based is broadcast.
This does not reduce the amount of message traffic in the normal case, since we are cheating there by not broadcasting input and taking some risk from faulty clients. Thus there is no performance gain to balance the large loss from doing public key operations, except when there are lots of faulty clients.
8.7 Performance using multicast
We separate the client-Paxos costs from the internal costs. They are not really comparable, for two reasons:
They often involve a network with very different properties.
Internal traffic can often have much bigger batches since it can combine the traffic from all the clients.
Figure 5 shows that in the normal case BP has one client-agents round trip (ng is a good quorum), by comparison with a client-primary round-trip in CP. In addition, there is one 1→n message from the primary as in CP, and two n→n messages among the agents, compared with one n→1 message to the primary in CP, and one 1→n message from the primary that can go in parallel with output. Thus BP has one extra message latency before the client gets output. What about throughput?
In a network that supports multicast efficiently (for example, any broadcast LAN or a switched LAN whose switches support it), the extra cost for n receivers is small. Table 1 shows the cost comparison on this assumption. BP is about twice as expensive as CP, or almost three times as expensive for the same number of failures (f or s). Itís not surprising that faults are much more costly.
If thereís no efficient multicast, agents can relay their messages to other agents through the primary, complete with authenticators, so that there are 2n messages after Choosea or Accepta rather than n2.
Table 1: Cost of
a normal run of BP and CP
|
Enables |
Message flow |
BP |
cost |
CP |
cost |
|
Inputp |
client→agents/primary |
1→n |
1 |
1→1 |
1 |
|
output |
agents/primary→client |
ng→1 |
f + 1 |
1→1 |
1 |
|
Total external |
†f + 2 |
2 |
|||
|
Choosea |
primary→agents |
1→n-1 |
1 |
|
|
|
Accept |
agents/primary→agents |
n-1→n |
n-1 |
1→n-1 |
1 |
|
Finish |
agents→agents/primary |
n→n |
n |
n-1→1 |
n-1 |
|
Finisha |
primary→agents |
|
|
1→n-1 |
0 |
|
Total internal |
2n |
n |
|||
|
Smallest
non-trivial n |
f† = 1 |
s = 1 |
|||
8.8 Optimizations
The optimizations of AP work in BP: compressing state with the last-triple, using one view change for many steps, and batching.
BP does not have to transmit the clientís entire input in each message. Itís sometimes enough to just send an Ďauthenticatorí, a signature of the message implemented by hashing it with a key shared between sender and receiver.
An undesirable property of BPís view change is that the agents must remember all their cwa values, since they donít know which one might be needed. This means that the last-triple optimization is not enough to avoid storage linear in the number of views. To avoid this, notice that if x ő anchorvp then x ő anchorv is broadcast by (B7), so if agent a is the primary for v then a can discard cwa for all w < v, since these are only needed for finding an element of anchorw, and anchorw anchorv. For this to work, each agent a′ must remember its contribution to x ő anchorv. If anchorva′ = {cva′}, remembering cva′ is enough. If anchorva′ = X, then a′ must remember that; this is a new requirement. An agent must remember at most n values of cwa or anchorwa = X before its turn as primary comes along. If agents donít act as primaries, then they need to collect the Ancvx,a facts themselves at regular intervals.
An agentís inputa need not be persistent, because of the way input is defined as a history variable. If an agent discards input, however, the clients might have to retransmit their inputs.
Itís unfortunate that the primary has a persistent cvp. If itís also an agent, then this can be the agentís cva, so the only cost is that it must be persisted before itís sent to any other agent. To get a primary with no persistent state, follow the model of CP: introduce a volatile cp, make cvp a history variable, and maintain invariants corresponding to (C1) and (C8) as in section 7.3:
|
invariant |
cpv≠ nil ř cp = cvp |
|
(B10) |
|
|
Qdec[ru*=nil] Ŕ v > u ř† cvp = nil |
|
(B11) |
To do Choosevp the primary must establish cvp = nil using (B11). This may require a new view; to preserve the round-robin scheduling of primaries, make a V a pair (i, j), where i determines the primary (p(i, j) = i mod n) and p can use j to start another view.
9 Conclusion
We started with an abstract Paxos algorithm AP that uses n agents and has only the agent actions Close, Accept, and Finish and an abstract Choose (plus the external actions Input and Decision). AP works by running a sequence of views until thereís one that runs for long enough to make a visible decision quorum for some input. Provided no later view starts, this will always happen as long as the choice is made and is visible. APís operation is divided into view change and normal operation; the latter requires one round-trip of agent-agent communication. AP can do any number of successive decisions with a single view change plus one normal operation per decision. APís agents are memories that can do conditional writes, but DP is a generalization that works with read-write memories.
AP canít be implemented directly because it has actions that touch state at more than one process, in particular the Choosev action. We showed two implementations in which the processes communicate stable predicates about their state that are strong enough to convey all the information that APís actions need. Both CP and BP have essentially the same agent actions as AP. Both implement APís Anchor and Choose actions in a primary process that is logically separate, though it practice it is combined with an agent unless the agents are disks.
CP also uses the primary to relay information among the agents. It doesnít tolerate any faults. It needs Qout and Qdec exclusive for safety, and live for liveness. For size-based quorums we have f = 0, s < n/2 and Qout = Qdec = Q≥s+1. In normal operation there are n internal messages if a multicast counts as 1, and the client latency is one client-primary round-trip plus one primary-agent round trip.
BP does tolerate faults, so it needs Anchor and Choose actions at both agents and primary, and uses multicast to share information among agents. In addition to CPís requirements on quorums, it also needs Qch exclusive with itself for safety, and Qch live and Qch Õ Q~F+ for liveness. For size-based quorums and F ř S we have Q~F = Q≥f+1 and Q~F+ = Qout = Qdec = Qch = Q≥2f+1. In normal operation there are 2n internal messages, and CPís primary-agent round-trip is replaced by a primary-agent multicast plus an agent-agent round trip.
The main application for Paxos is replicated state machines.
References
[1]
Castro, M. and Liskov, B.
Practical Byzantine fault tolerance. Proc. 3rd OSDI,
[2]
Castro, M. and Liskov, B. Proactive recovery in
a Byzantine-fault-tolerant system. Proc. 4th OSDI,
[5]
Fischer, M., Lynch, N., and
[6] Gafni, E. and Lamport, L. Disk Paxos. Proc. DISC 2000, LNCS 1914, Springer, 2000, 330-344.
[7] Gray, J. and Reuter, A. Transaction Processing: Concepts and Techniques. Morgan Kaufmann, 1993.
[9] Lamport, L. A simple approach to specifying concurrent systems. Comm. ACM 32, 1, Jan. 1989, 32-45.
[10] Lamport,
L. The part-time parliament. ACM Transactions on Computer Systems 16, 2, May 1998, 133-169. Originally
appeared as Research Report 49,
[11] Lampson,
B., Lynch, N., and SÝgaard-Andersen, J. Correctness of at-most-once message
delivery protocols. Proc. 6th Conf. on Formal Description Techniques,
[14] Liskov, B. and Oki, B. Viewstamped replication, Proc. 7th PODC, Aug. 1988.
[15] Lynch, N. Distributed Algorithms. Morgan Kaufmann, 1996.
[16] Malkhi,
D.† and Reiter, M. Byzantine quorum
systems. In Proc. 29th ACM STOC,
Appendix
Table 2 gives some correspondences between the terminology of this paper and that of Castro and Liskov.
Table 3 lists all the names for variables and constants in alphabetical order, followed by the @, #, [], and Q+ notation and the names of the actions for communication.
Table 4 collects the variables, abstractions, state functions, actions, and invariants of AP, CP, and BP to help you see how they are related. To save space, we shorten the names of actions to two characters, and shorten input, active, and anchor to in, act, and anc.
The external actions are first, then the internal ones in the order of a complete run. Changes from the item to the left are marked by boxes except for p and a superscripts. A ditto mark " means that the entry is a copy of the corresponding entry to the left.
The legend in the lower left corner summarizes the way we mark non-local, changed, and abstract variables. We mark as non-local anything in an action that came from other processes, even though in CP and BP it is of course local when the action occurs.
Figure 6 collects from figures 3-5 the pictures for the flow of actions and messages in AP, CP, and BP. Notice the fact that they start slightly differently, the extra Choose action in BP, and the extra Finisha action in CP.
Table 2: Our terminology for BP vs. Castro and Liskovís
|
Action→ |
C-L
state |
Our
state |
C-L
msg |
Our
msg |
|
Closep |
|
|
view-change |
ra, ca |
|
Anchorva |
in view v |
anchorva ≠ {} |
view-ack |
anchorva |
|
Anchorvp |
in view v |
anchorvp ≠ {} |
new-view |
|
|
Choosep |
pre-prepared |
cvp ≠ nil |
pre-prepare |
cvp |
|
Choosea |
pre-prepared |
cva ≠ nil |
prepare |
cva |
|
Accept |
prepared |
rva ≠ nil |
commit |
rva |
|
Finish |
committed |
da
≠
nil |
|
|
|
Q~F |
weak certificate |
|
|
|
|
Q~F+ |
quorum certificate |
|
|
|
Table 3: Variables, constants, notation, and communication
|
|
|
|
|
|
|
|
|
|
|
|
Spec, |
AP |
DP |
CP |
BP |
|
|
|
|
failure, quorum |
|
Δ from AP |
Δ from |
Δ from CP |
|
|
in section |
|
ß 2, 3 |
ß 4 |
ß 5 |
ß 7 |
ß 8 |
|
|
Agent |
a |
|
a |
|
|
|
|
|
Choice |
c |
|
cv |
|
cp |
cva, ceva, cvp |
|
|
Decision |
d |
d |
da |
|
|
|
|
|
Faulty |
|
f,
Fm |
|
|
|
|
|
|
predicate |
g,
G |
|
|
|
|
|
|
|
Integer |
i,
j |
|
|
|
|
|
|
|
process |
k,
m |
|
|
|
|
|
|
|
|A| |
|
n |
|
|
|
|
|
|
Primary |
p |
|
|
|
p,
pv |
|
|
|
Quorum |
Q,
q |
Q~F, Q+ |
Qdec, Qout |
|
|
Qch |
|
|
Result |
r |
|
rva, rv |
rxva, rova |
revp |
reva, |
|
|
Stopped |
|
s,
Sm |
|
|
|
|
|
|
Truth |
T |
T
(ß6) |
|
|
|
|
|
|
View |
u,
v,
w |
|
v |
|
vp |
|
|
|
value |
x,
y |
|
|
|
|
|
|
|
failures |
Z,
z |
ZF, ZS, ZFS |
|
|
|
|
|
|
g@m |
Tm ř g |
Communication
|
|
G@m |
(λ k | Gk@m) |
|
|
Q#G |
{m | Gm ŕ Fm} őQ |
Localk(g) |
|
Q[rv*=x] |
Q#(λ m | rvm=x) |
Transmit†† k,m(g) |
|
Q+ |
{q′ | ("z ő ZFS | q′ Ė z ő Q} |
TransmitFk,m(g) |
|
Q~F |
{q | q Ō ZF} |
Broadcast m†† (g) |
![]()
![]()
 ††††††††
†††††††† 
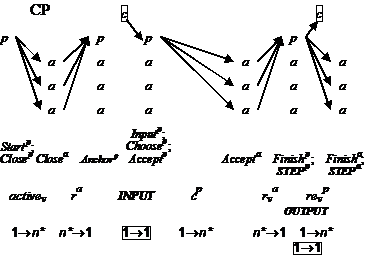

Figure 6: Summary of actions