This document was made by OCR from a scan of the technical report. It has not been edited or proofread and is not meant for human consumption, but only for search engines. To see the scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL that got you here.

IF Lookups using Multiway and Multicolumn

Search

Butler Lampson, V Srinivasan and George Varghese
blampson@microsoft.com,cheenu@dworkin.wustl.edu,varghese@dworkin.wustl.edu

Abstract- IP address lookup is becoming critical because of increasing routing table size, speed, and traffic in the Inter­net. Our paper shows how binary search can be adapted for best matching prefix using two entries per prefix and by doing precomputation. Next we show how to improve the performance of any best matching prefix scheme using an initial array indexed by the first X bits of the address. We then describe how to take advantage of cache line size to do a multiway search with 6-way branching. Finally, we show how to extend the binary search solution and the multiway search solution for IPv6. For a database of N prefixes with address length W, naive binary search scheme would take O(W * logN); we show how to reduce this to O(W + logN) us­ing multiple column binary search. Measurements using a practical (Mae-East) database of 30000 entries yield a worst case lookup time of 490 nanoseconds, five times faster than the Patricia trie scheme used in BSD UNIX. Our scheme is attractive for IPv6 because of small storage requirement (2N nodes) and speed (estimated worst case of 7 cache line reads)

Keywords— Longest Prefix Match, IP Lookup

I. INTRODUCTION

Statistics show that the number of hosts on the inter-net is tripling approximately every two years [oT]. Traffic on the Internet is also increasing exponentially. Traffic in­crease can be traced not only to increased hosts, but also to new applications (e.g., the Web, video conferencing, re­mote imaging) which have higher bandwidth needs than traditional applications. One can only expect further in­creases in users, hosts, domains, and traffic. The possibility of a global Internet with multiple addresses per user (e.g., for appliances) has necessitated a transition from the older Internet routing protocol (IPv4 with 32 bit addresses) to the proposed next generation protocol (IPv6 with 128 bit addresses).

High speed packet forwarding is compounded by increas­ing routing database sizes (due to increased number of hosts) and the increased size of each address in the database (due to the transition to IPv6). Our paper deals with the problem of increasing IP packet forwarding rates in routers. In particular, we deal with a component of high speed for­warding, address lookup, that is considered to be a major bottleneck.

When an Internet router gets a packet P from an input link interface, it uses the destination address in packet P to lookup a routing database. The result of the lookup provides an output link interface, to which packet P is forwarded. There is some additional bookkeeping such as updating packet headers, but the major tasks in packet for­warding are address lookup and switching packets between link interfaces.

For Gigabit routing, many solutions exist which do fast switching within the router box [NMH9T]. Despite this, the problem of doing lookups at Gigabit speeds remains. For example, Ascend's product [Asc] has hardware assistance for lookups and can take up to 3 ps for a single lookup in the worst case and 1 ps on average. However, to support say 5 Gbps with an average packet size of 512 bytes, lookups need to be performed in 800 nsec per packet. By contrast, our scheme can be implemented in software on an ordinary PC in a worst case time of 490 nsec.

The Best Matching Prefix Problem: Address

lookup can be done at high speeds if we are looking for an exact match of the packet destination address to a corre­sponding address in the routing database. Exact matching can be done using standard techniques such as hashing or binary search. Unfortunately, most routing protocols (in­cluding OSI and IP) use hierarchical addressing to avoid scaling problems. Rather than have each router store a database entry for all possible destination IP addresses, the router stores address prefixes that represent a group of addresses reachable through the same interface. The use of prefixes allows scaling to worldwide networks.

The use of prefixes introduces a new dimension to the lookup problem: multiple prefixes may match a given ad­dress. If a packet matches multiple prefixes, it is intuitive that the packet should be forwarded corresponding to the most specific prefix or longest prefix match. IPv4 prefixes are arbitrary bit strings up to 32 bits in length as shown in Table I. To see the difference between the exact match­ing and best matching prefix, consider a 32 bit address A whose first 8 bits are 10001111. If we searched for A in the above table, exact match would not give us a match. However prefix matches are 100* and 1000*, of which the best matching prefix is 1000*, whose next hop is L5.

Prefix

Next hop

'

L9

001'

L1

0001'

L2

011111'

L3

100'

L4

1000'

L5

10001'

L6

 

TABLE I
A sample routing table

Paper Organization:

The rest of this paper is organized as follows. Section II describes related work and briefly describes our contribu‑

tion. Section III contains our basic binary search scheme. Section IV describes a basic idea of using an array as a front end to reduce the number of keys required for binary search. Section V describes how we exploit the locality in­herent in cache lines to do multiway binary search; we also describe measurements for a sample large IPv4 database. Section VII describes how to do multicolumn and multiway binary search for IPv6. We also describe some measure­ments and projected performance estimates. Section VIII states our conclusions.

II. PREVIOUS WORK AND OUR CONTRIBUTIONS

[MTW95] uses content-addressable memories (CAMs) for implementing best matching prefix. Their scheme uses a separate CAM for each possible prefix length. For IPv4 this can require 32 CAMs and 128 CAMs for IPv6, which is expensive.

The current NetBSD implementation [SW95] , [Skl] uses a Patricia Trie which processes an address one bit at a time. On a 200 MHz pentium, with about 33,000 entries in the routing table, this takes 1.5 to 2.5 p s on the av­erage. These numbers will worsen with larger databases. [Skl] mentions that the expected number of bit tests for the patricia tree is 1.44 log N, where N is the number of entries in the table. For N 32000, this is over 21 bit tests. With memory accesses being very slow for modern CPUs, 21 memory accesses is excessive. Patricia tries also use skip counts to compress one way branches, which necessitates backtracking. Such backtracking slows down the algorithm and makes pipelining difficult.

Many authors have proposed tries of high radix [PZ92] but only for exact matching of addresses. OSI address lookups are done naturally using trie search 4 bits at a time [Per92] but that is because OSI prefix lengths are al­ways multiples of 4. Our methods can be used to lookup OSI address lookups 8 bits at a time.

Our basic binary tree method is described very briefly in a page in [Per92], based on work by the first author of this paper.' However, the ideas of using an initial array, multicolumn and multiway binary search (which are cru­cial to the competitiveness of our scheme) have never been described before. Our description also has actual measure­ments, and an explanation of algorithm correctness.

[NMH9T] claims that it is possible to do a lookup in 200 nsec using SRAMs (with 10 nsec cycle times) to store the entire routing database. We note that large SRAMs are extremely expensive and are typically limited to caches in ordinary processors.

Caching is a standard solution for improving average performance. However, experimental studies have shown poor cache hit ratios for backbone routers[NMH9T]. This is partly due to the fact that caches typically store whole addresses. Finally, schemes like Tag and Flow Switching suggest protocol changes to avoid the lookup problem alto­gether. These proposals depend on widespread acceptance, and do not completely eliminate the need for lookups at

'This can be confirmed by Radia Perlman.network boundaries.

In the last year, two new techniques [BCDP9T], [WVTP9T] for doing best matching prefix have been an­nounced. We have been unable to find details of the re­sults in [BCDP9T] (it will appear in a few months), except to know that the approach is based on compressing the database so that it will fit into the cache. The approach in [WVTP9T] is based on doing binary search on the possible prefix lengths.

Our Contributions:

In this paper, we start by showing how to modify bi­nary search to do best matching prefix. Our basic binary search technique has been described briefly in Perlman's book [Per92] but is due to the first author of this paper and has never been published before. The enhancements to the use of an initial array, multicolumn and multiway search, implementation details, and the measurements have never been described before.

Modified binary search requires two ideas: first, we treat each prefix as a range and encode it using the start and end of range; second, we arrange range entries in a binary search table and precompute a mapping between consecu­tive regions in the binary search table and the correspond­ing prefix.

Our approach is completely different from either [BCDP9T], [WVTP9T] as we do binary search on the num­ber of possible prefixes as opposed to the number of pos­sible prefix lengths.. For example, the naive complexity of our scheme is log2 N + 1 memory accesses, where N is the number of prefixes; by contrast, the complexity of the [WVTP9T] scheme is log2 W hash computations plus mem­ory accesses, where W is the length of the address in bits.

At a first glance, it would appear that the scheme in [WVTP9T] would be faster (except potentially for hash computation, which is not required in our scheme) than our scheme, especially for large prefix databases. How­ever, we show that we can exploit the locality inherent in processor caches and fast cache line reads using SDRAM or RDRAM to do multiway search in logk+, N + 1 steps, where k > 1. We have found good results using k 5. By contrast, it appears to be impossible to modify the scheme in [WVTP9T] to do multiway search on prefix lengths be­cause each search in a hash table only gives two possible outcomes.

Further, for long addresses (e.g., 128 bit IPv6 addresses), the true complexity of the scheme in [WVTP9T] is closer to O(W/M) log2 W, where M is the word size of the machine.2 This is because computing a hash on a W bit address takes O(W/M) time. By contrast, we introduce a multicolumn binary search scheme for IPv6 and OSI addresses that takes log2 N + W/M + 1. Notice that the W/M factor is addi­tive and not multiplicative. Using a machine word size of M 32 and an address width W of 128, this is a potential multiplicative factor of 4 that is avoided in our scheme. We contrast the schemes in greater detail later.

2The scheme in mvt starts by doing a hash of W/2 bits; it can then do a hash on 3W/4 bits, followed by 7W/8 bits etc. Thus in the worst case, each hash may operate on roughly 3W/4 bits.

We also describe a simple scheme of using an initial array as a front end to reduce the number of keys required to be searched in binary search. Essentially, we partition the original database according to every possible combination of the first X bits. Our measurements use X 16. Since the number of possible prefixes that begin with a particular combination of the first X bits is much smaller than the total number of prefixes, this is a big win in practice.

Our paper describes the results of several other measure­ments of speed and memory usage for our implementations of these two schemes. The measurements allow us to isolate the effects of individual optimizations and architectural fea­tures of the CPUs we used. We describe results using a publically available routing database (Mae-East NAP) for IPv4, and by using randomly chosen 128 bit addresses for IPv6.

Our measurements show good results. Measurements us­ing the (Mae-East) database of 30000 entries yield a worst case lookup time of 490 nanoseconds, five times faster than the performance of the Patricia trie scheme used in BSD UNIX used on the same database. We also estimate the performance of our scheme for IPv6 using a special SDRAM or RDRAM memory (which is now commercially available though we could not obtain one in time to do actual ex­periments). This memory allows fast access to data within a page of memory, which enables us to speed up multiway search. Thus we estimate a worst case figure of 7 cache line reads for a large database of IPv6 entries.

Please note that in the paper, by memory reference we mean accesses to the main memory. Cache hits are not counted as memory references. So, if a cache line of 32 bytes is read, then accessing two different bytes in the 32 byte line is counted as one memory reference. This is jus­tifiable, as a main memory read has an access time of 60 nsec while the on-chip L1 cache can be read at the clock speed of 5 nsec on an Intel Pentium Pro. With SDRAM or RDRAM, a cache line fill is counted as one memory ac­cess. With SDRAM a cache line fill is a burst read with burst length 4. While the first read has an access time of 60 nsec, the remaining 3 reads have access times of only 10 nsec each [Mic]. With RDRAM, an entire 32 byte cache line can be filled in 101 nsec [Ram].

III. ADAPTING BINARY SEARCH FOR BEST MATCHING

PREFIX

Binary search can be used to solve the best matching prefix problem, but only after several subtle modifications. Assume for simplicity in the examples, that we have 6 bit addresses and three prefixes 1*, 101*, and 10101*. First, binary search does not work with variable length strings. Thus the simplest approach is to pad each prefix to be a 6 bit string by adding zeroes. This is shown in Figure 1.

Now consider a search for the three 6 bit addresses 101011, 101110, and 111110. Since none of these addresses are in the table, binary search will fail. Unfortunately, on a failure all three of these addresses will end up at the end of the table because all of them are greater than 101010, which is the last element in the binary search table. Notice

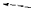
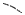
Text Box: 1 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0Text Box: Text Box: Text Box: should go here Text Box: 101011 101110 111110Fig. 1. Placing the three prefixes 1*, 101*, and 10101* in a binary search table by padding each prefix with 0's to make 6 bit strings and sorting the resulting strings. Note that the addresses 101011, 101110, and 111110 all end up in the same region in the binary search table

however that each of these three addresses (see Figure 1) has a different best matching prefix.

Thus we have two problems with naive binary search: first, when we search for an address we end up far away from the matching prefix (potentially requiring a linear search); second, multiple addresses that match to differ­ent prefixes, end up in the same region in the binary table (Figure 1).

Encoding Prefixes as Ranges:

To solve the second problem, we recognize that a prefix like 1* is really a range of addresses from 100000 to 111111. Thus instead of encoding 1* by just 100000 (the start of the range), we encode it using both the start and end of range. Thus each prefix is encoded by two full length bit strings. These bit strings are then sorted. The result for the same three prefixes is shown in Figure 2. We connect the start and end of a range (corresponding to a prefix) by a line in Figure 2. Notice how the ranges are nested. If we now try to search for the same set of addresses, they each end in a different region in the table. To be more precise, the search for address 101011 ends in an exact match. The search for address 101110 ends in a failure in the region between 101011 and 101111 (Figure 2), and the search for address 111110 ends in a failure in the region between 101111 and 111111. Thus it appears that the second problem (multiple addresses that match different prefixes ending in the same region of the table) has disappeared. Compare Figure 1 and Figure 2.

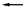
Text Box: Text Box: Text Box: Text Box: Text Box: Text Box: 101011 101110 1111101 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1

Fig. 2. We now encode each prefix in the table as a range using two values: the start and end of range. This time the addresses that match different prefixes end up in different ranges.

To see that this is a general phenomenon, consider Figure 3. The figure shows an arbitrary binary search table after every prefix has been encoded by the low (marked L in Figure 3) and its high points (marked H) of the corre­sponding range. Consider an arbitrary position indicated by the solid arrow. If binary search for address A ends up at this point, which prefix should we map A to? It is easy

to see the answer visually from Figure 3. If we start from the point shown by the solid arrow and we go back up the table, the prefix corresponding to A is the first L that is not followed by a corresponding H (see dotted arrow in Figure 3.)

Why does this work? Since we did not encounter an H corresponding to this L, it clearly means that A is con­tained in the range corresponding to this prefix. Since this is the first such L, this is the smallest such range. Es­sentially, this works because the best matching prefix has been translated to the problem of finding the narrowest enclosing range.

Text Box: L L L L H H L L, H H H H Text Box: Text Box: Fig. 3. Why each range in the modified binary search table maps to a unique prefix.

A. Using Precomputationto Avoid Search

Unfortunately, the solution depicted in Figure 2 and Figure 3 does not solve the first problem: notice that bi­nary search ends in a position that is far away (potentially) from the actual prefix. If we were to search for the prefix (as described earlier), we could have a linear time search.

However, the modified binary search table shown in Figure 3 has a nice property we can exploit. Any region in the binary search betweentwo consecutive numbers cor­responds to a unique prefix. As described earlier, the prefix corresponds to the first L before this region that is not matched by a corresponding H that also occurs before this region. Similarly, every exact match corresponds to a unique prefix.

But if this is the case, we can precompute the prefix corresponding to each region and to each exact match. This can potentially slow down insertion. However, the insertion or deletion of a new prefix should be a rare event (the next hop to reach a prefix may change rapidly, but the addition of a new prefix should be rare) compared to packet forwarding times. Thus slowing down insertion costs for the sake of faster forwarding is a good idea. Essentially, the idea is to add the dotted line pointer shown in Figure 3 to every region.

The final table corresponding to Figure 3 is shown in Figure 5. Notice that with each table entry E, there are two precomputed prefix values. If binary search for address A ends in a failure at E, it is because A > E. In that case, we use the > pointer corresponding to E. On the other hand, if binary search for address A ends in a match at E, we use the    pointer.

Notice that for an entry like 101011, the two entries are different. If address A ends up at this point and is greater than 101011, clearly the right prefix is P2                                  101*. Onthe other hand, if address A ends up at this point with equality, the correct prefix is P3 10101*. Intuitively, if an address A ends up equal to the high point of a range R, then A fall within the range R; if A ends up greater than the high point of range R, then A falls within the smallest range that encloses range R.

Our scheme is somewhat different from the description in [Per92]. We use two pointers per entry instead of just one pointer. The description of our scheme in [Per92] sug­gests padding every address by an extra bit; this avoids the need for an extra pointer but it makes the implementation grossly inefficient because it works on 33 bit (i.e., for IPv4) or 129 bit (i.e., for IPv6) quantities. If there are less than 216 different choices of next hop, then the two pointers can be packed into a 32 bit quantity, which is probably the minimum storage needed.

 

 

 

 

 

 

 

> 

=

P1)

1

0

0

0

0

0

P1

P1

P2)

1

0

1

0

0

0

P2

P2

P3)

1

0

1

0

1

0

P3

P3

 

1

0

1

0

1

1

P2

P3

 

1

0

1

1

1

1

P1

P2

 

1

1

1

1

1

1

−

P1

 

Fig. 4. The final modified binary search table with precomputed prefixes for every region of the binary table. We need to distinguish between a search that ends in a success at a given point (= pointer) and search that ends in a failure at a given point (> pointer).

B. Insertioninto a Modified Binary Search Table

The simplest way to build a modified binary search table from scratch is to first sort all the entries, after marking each entry as a high or a low point of a range. Next, we process the entries, using a stack, from the lowest down to the highest to precompute the corresponding best matching prefixes. Whenever we encounter a low point (L in the figures), we stack the corresponding prefix; whenever we see the corresponding high point, we unstack the prefix. Intuitively, as we move down the table, we are keeping track of the currently active ranges; the top of the stack keeps track of the innermost active range. The prefix on top of the stack can be used to set the > pointers for each entry, and the pointers can be computed trivially. This is an O(N) algorithm if there are N prefixes in the table.

One might hope for a faster insertion algorithm if we had to only add (or delete) a prefix. First, we could represent the binary search table as a binary tree in the usual way. This avoids the need to shift entries to make room for a new entry. Unfortunately, the addition of a new prefix can affect the precomputed information in O(N) prefixes. This is illustrated in Figure 5. The figure shows an outermost range corresponding to prefix P; inside this range are N - 1 smaller ranges (prefixes) that do not intersect. In the regions not covered by these smaller prefixes, we map to P. Unfortunately, if we now add Q (Figure 5), we cause all these regions to map to Q, an O(N) update process.

Thus there does not appear to be any update technique

Text Box: Text Box: L L H L H L H L H H Prefix P Prefix Q

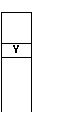Text Box: Y Fig. 5. Adding a new prefix Q (dotted line) can cause all regions between an H and an L to move from Prefix P to Prefix Q.

pointer to binary tree

Text Box: x

Text Box: Binary Tree of keys starting with X Fig. 6. The array element with index X will have the best matching prefix of X (say Y) and a pointer to a binary tree/table of all prefixes that have X as a prefix.

that is faster than just building a table from scratch. Of course, many insertions can be batched; if the update pro­cess falls behind, the batching will lead to more efficient updates.

IV. PRECOmPUTEd 16 BIT PREFIX TABLE

We can improve the worst case number of memory ac­cesses of the basic binary search scheme with a precom­puted table of best matching prefixes for the first Y bits. The main idea is to effectively partition the single binary search table into multiple binary search tables for each value of the first Y bits. This is illustrated in Figure 6. We choose Y 16 for what follows as the table size is about as large as we can afford, while providing maximum partitioning.

Without the initial table, the worst case possible num­ber of memory accesses is log2N + 1, which for large databases could be 16 or more memory accesses. For a sample database, this simple trick of using an array as a front end reduces the maximum number of prefixes in each partitioned table to 336 from the maximum value of over 30,000.

Text Box: Text Box: "hist"Text Box: 500 450 400 350 300 250 200 150 100 50 0 The best matching prefixes for the first 16 bit prefixes can be precomputed and stored in a table. This table would then have Max 65536 elements. For each index X of the array, the corresponding array element stores best matching prefix of X. Additionally, if there are prefixes of longer length with that prefix X, the array element stores a pointer to a binary search table/tree that contains all such prefixes. Insertion, deletion, and search in the individual binary search tables is identical to the technique described earlier in Section III.0                                  50                                          100                                       150                                       200                                       250                                       300

Fig. 7. For each 16 bit prefix X, let N(X) be the number of prefixes that have X as a prefix. The histogram shows the distribution of N(X) for the Mae-East NAP Routing database [Mer]. The horizontal axis represents N(X) and the vertical axis represents the number of tables with a given value of N(X). Thus the peak of the histogram says that there are 484 binary search tables with only 2 keys. There is only 1 binary search table with the worst case number of 336 keys.

Figure 7 shows the distribution of the number of keys that would occur in the individual binary search trees for a publically available IP backbone router database [Mer] after going through an initial 16 bit array. The largest number of keys in any binary table is found to be 336, which leads to a worst case of 10 memory accesses.

V. MULTIWAY BINARY SEARCH: EXPLOITING THE

CACHE LINE

Todays processors have wide cache lines. The Intel Pen­tium Pro has a cache line size of 32 bytes. Main memory is usually arranged in a matrix form, with rows and columns. Accessing data given a random row address and column ad­dress has an access time of 50 to 60 nsec. However, using SDRAM or RDRAM, filling a cache line of 32 bytes is much faster, which is a burst access to 4 contiguous 64 bit DRAM locations, is much faster than accessing 4 random DRAM locations. When accessing a burst of contiguous columns in the same row, while the first piece of data would be avail­able only after 60 nsec, further columns would be available much faster. SDRAMs (Synchronous DRAMs) are avail­able (at $205 for 8MB [Sim]) that have a column access time of 10 nsec. Timing diagrams of micron SDRAMs are available through [Mic]. RDRAMs [Ram] are available that can fill a cache line in 101 nsec. The Intel Pentium pro has a 64 bit data bus and a 256 bit cacheline [Inta]. Detailed descriptions of main memory organization can be found in [HP96].

The significance of this observation is that it pays to re­structure data structures to improve locality of access. To make use of the cache line fill and the burst mode, keys and pointers in search tables can be laid out to allow multiway search instead of binary search. This effectively allows us to reduce the search time of binary search from log2 N to logk +1 N, where k is the number of keys in a search node. The main idea is to make k as large as possible so that a single search node (containing k keys and 2k + 1 pointers)

fits into a single cache line. If this can be arranged, an access to the first word in the search node will result in the entire node being prefetched into cache. Thus the accesses to the remaining keys in the search node are much cheaper than a memory access.

We did our experiments using a Pentium Pro; the pa­rameters of the Pentium Pro resulted in us choosing k = 5 (i.e, doing a six way search). For our case, if we use k keys per node, then we need 2k + 1 pointers, each of which is

a 16 bit quantity. So in 32 bytes we can place 5 keys and hence can do a 6-way search. For example, if there are keys k1..k8, a 3-way tree is given in Figure 8. The initial full array of 16 bits followed by the 6-way search is depicted in Figure 9.

Text Box: Text Box: k1 k2Text Box: k3 k6Text Box: k4 k5Text Box: Node pointerText Box: k7 k8info                 info info info info info info info info

Fig. 8. 3-way tree for 8 keys

Text Box: Text Box: 16 bitsText Box: 32 bytesText Box: index intoText Box: 6-way search tableText Box: info pointerFig. 9. The initial 16 bit array, with pointers to the corresponding 6-way search nodes.

This shows that the worst case (for the Mae East database after using a 16 bit initial array) has 336 en­tries leading to a worst case of 4 memory accesses (since 64 =1296 takes only 4 memory accesses when doing a 6-way search).

Each node in the 6-way search table has 5 keys k1 to k5, each of which is 16 bits. There are equal to pointers p1 to p5 corresponding to each of these keys. Pointers p01 to p56 correspond to ranges demarcated by the keys. This is shown in Figure 10 . Among the keys we have the relation k < k +1. Each pointer has a bit which says it is an informationpointer or a next node pointer.

A. Search

The following search procedure can be used for both IPv4 and IPv6. For IPv6, 32 bit keys can be used instead of 16 bits.

Text Box: C = 32 bytes (cache line size)Text Box: Text Box: Node 1Text Box: Node 2Text Box: Node 3Text Box: Node iText Box: Node nA single 32 byte node

 

k1

 

k2

 

k3

 

k4

 

k5

 

p01

p1

p12

p2

p23

p3

p34

p4

p45

p5

p56

 

Fig. 10. The structure of the 6-way search node. There are k keys and 2k + 1 pointers.

1.   Index into the first 16 bit array using the first 16 bits of the address.

2.   If the pointer at the location is an information pointer, return it. Otherwise enter the 6-way search with the initial node given by the pointer, and the key being the next 16 bits of the address.

3. In the current 6-way node locate the position of the key among the keys in the 6-way node. We use binary search among the keys within a node. If the key equals any of the keys key in the node, use the corresponding pointer ptr . If the key falls in any range formed by the keys, use the pointer ptr , +1. If this pointer is an information pointer, return it; otherwise repeat this step with the new 6-way node given by the pointer.

In addition, we allow multicolumn search for IPv6 (see Section VII) as follows. If we encounter an equal to pointer, the search shifts to the next 16 bits of the input address. This feature can be ignored for now and will be understood after reading Section VII.

As the data structure itself is designed with a node size

equal to a cache line size, good caching behavior is a conse‑

quence. All the frequently accessed nodes will stay in the

cache. To reduce the worst case access time, the first few

levels in a worst case depth tree can be cached.

VI. MEAsuREmENTs AND CompARisoN FoR IPv4

We used a Pentium Pro [Intb] based machine, with a 200 MHz clock (cost under 5000 dollars). It has a 8 KByte four-way set-associative primary instruction cache and a 8 KByte dual ported two-way set associative primary data cache. The L2 cache is 256 KBytes of SRAM that is cou­pled to the core processor through a full clock-speed, 64-bit, cache bus.

We used a practical routing Table with over 32000 en­tries that we obtained from [Mer for our experiments. Our tables list results for the BSD Radix Trie implementation

(extracted from the BSD kernel into user space), binary search (Bsearch) and 6-way search.

Repeated lookup of a single address: After adding

the routes in the route database VI, random IP addresses were generated and a lookup performed 10 million times for each such address. We picked 7 of these results to display in Table II.

 

Patricia

Basic binary search

16 bit +binary search

16 bit +6 way search

Time (nsec)

Time (nsec)

Time (nsec)

Time (nsec)

1530 1525 1450 2585 1980 810 1170

1175 990 1140 1210 1440 1220 1310

730 620 470 400 330 90 90

490 490 390 300 210 95 90

TABLE II
Time taken for single address lookup on a Pentium pro. Several
addresss were searched and the search times noted. Shown in the table
are addresses picked to illustrate the variation in time of the 16 bit
initial table+6-way search method. Thus the first two rows correspond
to the maximum depth of the search tree while the last two rows
correspond to the minimum depth (i.e, no prefixes in search table).

Average search time: 10 million IP addresses were generated and looked up, assuming that all IP addresses were equally probable. It was found that the average lookup time was 130 nanoseconds.

Memory Requirements and Worst case time

 

 

Patr icia

Basic Binary Search

16 bit
table
+binary

16 bit
table
+6 way

Mem for building(MB)

3.2

3.6

1

1

Mem for searchable structure (MB)

3.2

1

0.5

0.7

Worst case search (nsec)

2585

1310

730

490

Worst case faster than Patricia by

1

2

3.5

5

TABLE III
Memory Requirement and Worst case time

The memory requirement for the 6-way search is less than that for basic binary search! Though at first this looks counter-intuitive, this is again due to the initial 16 bit array. While the keys used in the regular binary search are 32 bits and the pointers involved are also 32 bits, in the 16 bit table followed by the 6-way search case, both the keys and the pointers are 16 bits.

From Table III we can see that the initial array improves the performance of the binary search from a worst case of 1310 nsec to 730 nsec; multiway search further improves

the search time to 490 nsec.

Instruction count:

The static instruction count for the search using a full 16 bit initial table followed by a 6-way search table is less than 100 instructions on the Pentium Pro. We also note that the gcc compiler uses only 386 instructions and does not use special instructions available in the pentium pro, using which it might be possible to further reduce the number of instructions.

VII. UsiNG MultiwAy AND MulticolumN SEARcH

FoR IPv6

In this section we describe the problems of searching for identifiers of large width (e.g., 128 bit IPv6 address or 20 byte OSI addresses). We first describe the basic ideas be­hind multicolumn search and then proceed to describe an implementation for IPv6 that uses both multicolumn and multiway search. We then describe sample measurements using randomly generated IPv6 addresses.

A. MulticolumnBinary Search of Large Identifiers

The scheme we have just described can be implemented efficiently for searching 32 bit IPv4 addresses. Unfortu­nately, a naive implementation for IPv6 can lead to ineffi­ciency. Assume that the word size M of the machine imple­menting this algorithm is 32 bits. Since IPv6 addresses are 128 bits (4 machine words), a naive implementation would take 4 . log2 (2N) memory accesses. For a reasonable sized table of around 32,000 entries this is around 60 memory accesses!

In general, suppose each identifier in the table is W/M words long (for IPv6 addresses on a 32 bit machine, W/M 4). Naive binary search will take W/M . logN comparisons which is expensive. Yet, this seems obviously wasteful. If all the identifiers have the same first W/M - 1 words, then clearly logN comparisons are sufficient. We show how to modify Binary Search to take log N + W/M comparisons. It is important to note that this optimization we describe can be useful for any use of binary search on long identifiers, not just the best matching prefix problem.

The strategy is to work in columns, starting with the most significant word and doing binary search in that col­umn until we get equality in that column. At that point, we move to the next column to the right and continue the binary search where we left off. Unfortunately, this does not quite work.

In Figure 11, which has W/M 3, suppose we are searching for the three word identifier BMW (pretend each character is a word). We start by comparing in the leftmost column in the middle element (shown by the arrow labeled 1). Since the B in BMW matches the B at the arrow labeled 1 we move to the right (not shown) and compare the M in BMW with the N in the middle location of the second column. Since N < M, we do the second probe at the quarter position of the second column. This time the two M's match and we move rightward and we find W, but (oops!) we have found AMW, not BMW which we were looking for.

Text Box: BMW? 2 3 A M W Text Box: A C E A D C W/M words

Text Box: Probe 1 B                                                   M       W

B                                                   N       X

B                                                   N       Y

B                                                   N         Z

C              N       D

Fig. 11. Binary Search by columns does not work when searching for

BMW

The problem is caused by the fact that when we moved to the quarter position in column 2, we assumed that all elements in the second quarter begin with B. This as­sumption is false in general. The trick is to add state to each element in each column which can contain the binary search to stay within a guard range.

In the figure, for each word like B in the leftmost (most significant) column, we add a pointer to the the range of all other words that also contain B in this position. Thus the first probe of the binary search for BMW starts with the B in BNX. On equality, we move to the second column as before. However, we also keep track of the guard range corresponding to the B's in the first column. The guard range (rows 4 through 6) is stored with the first B we compared.

Thus when we move to column 2 and we find that M in BMW is less than the N in BNX, we attempt to half the range as before and try a second probe at the third entry (the M in AMT). However the third entry is lower than the high point of the current guard range (4 through 6). So without doing a compare, we try to halve the binary search range again. This time we try entry 4 which is in the guard range. We get equality and move to the right, and find BMW as desired.

In general, every multiword entry W1, W2, . . ., W n will store a guard range with every word. The range for Wi, points to the range of entries that have W1, W2 , . . ., W i in the first i words. This ensures that when we get a match with W i in the i-the column, the binary search in column i + 1 will only search in this guard range. For example, the N entry in BNY (second column) has a guard range of 5 - 7, because these entries all have BN in the first two words.

The naive way to implement guard ranges is to change the guard range when we move between columns. However, the guard ranges may not be powers of 2, which will result in expensive divide operations. A simpler way is to follow the usual binary search probing. If the table size is a power of 2, this can easily be implemented. If the probe is not within the guard range, we simply keep halving the range until the probe is within the guard. Only then do we do a compare.

The resulting search strategy takes log2 N+W/M probes if there are N identifiers. The cost is the addition of two 16 bit pointers to each word. Since most word sizes are at least 32 bits, this results in adding 32 bits of pointer space for each word, which can at most double memory usage.

Once again, the dominant idea is to use precomputation to trade a slower insertion time for a faster search.

We note that the whole scheme can be elegantly rep­resented by a binary search tree with each node having the usual > and < pointers, but also an pointer which corresponds to moving to the next column to the right as shown above. The subtree corresponding to the pointer naturally represents the guard range.

B. Using Multicolumnand Multiway Search for IPv6

In this section we explore several possible ways of using the k-way search scheme for IPv6. With the 128 bit ad­dress, if we used columns of 16 bits each, then we would need 8 columns. With 16 bit keys we can do a 6-way search. So the number of memory accesses in the worst case would be log6 (2N) + 8. For N around 50,000 this is 15 memory accesses. In general, if we used columns of M bits, the worst case time would be logk+1N+W/M where W 128 for IPv6. The value of k depends on the cache linesize C. Since k keys requires 2k + 1 pointers, the following inequal­ity must hold. If we use pointers that are p bits long,

kM+(2k+ 1)*p< C

For the Intel Pentium pro, C is 32 bytes, i.e. 32 * 8 256

bits. If we use p   16,

k(M + 32) <       240, with the worst case time being
logk+1N + 128/M.

In general, the worst case number of memory accesses needed is T [(logk+1 (2N)1 + [(W/m)1, with the inequal­ity Mk+(2k+1)p < C, where N is the number of prefixes, W is the number of bits in the address, M is the number of bits per column in the multiple column binary search, k is the number of keys in one node, C is the cache linesize in bits, p is the number of bits to represent the pointers within the structure and T is the worst case number of memory accesses.

Fig 12 shows that the W bits in an IP address are divided into M bits per column. Each of these M bits make up a M bit key, k of which are to be fitted in the search node of length C bits along with 2k + 1 pointers of length p bits.

M (column size)

Text Box: W (address width in bits) M           p

key         pointer

C (cache line size)

Fig. 12. Symbols used in expressing the number of memory accesses needed.

For typical values of N, the number of prefixes, the fol­lowing table gives the value of the corresponding worst case number of memory accesses.

However, by using the initial array, the number of pre­fixes in a single tree can be reduced. For IPv4 the max­imum number in a single tree was 336 for a practical database with N more than 30000 (i.e., the number of pre­fixes that have the same first 16 bits is 168, leading to 336 keys). For IPv6, with p  16, even if there is an increase

 

No. of Prefixes

M = 16

M = 32

M = 64

128

12

10

8

256

13

10

8

1024

14

11

9

50000

17

15

13

100000

17

16

14

 

TABLE IV
Worst case number of memory accesses for various values of N and M
with W = 128; C = 256 (32 bytes) and p = 24 bits.

of 10 times in the number of prefixes that share the same first 16 bits, for 2048 prefixes in a tree we get a worst case of 9 cache line fills with a 32 byte cache line. For a 64 byte cache line machine, we get a worst case of 7 cache line fills. This would lead to worst case lookup times of less than 800 nsec, which is competitive with the scheme presented in [WVTP97].

C. Measurements

We generated random IPv6 prefixes and inserted into a k-way search with an initial 16 bit array. From the prac­tical IPv4 database, it was seen that with N about 30000, the maximum number which shared the first 16 bits was about 300, which is about 1of prefixes. To capture this, when generating IPv6 prefixes, we generated the last 112 bits randomly and distributed them among the slots in the first 16 bit table such that the maximum number that falls in any slot is around 1000. This is necessary because if the whole IPv6 prefix is generated randomly, even with N about 60000, only 1 prefix will be expected to fall in any first 16 bit slot. On a Pentium Pro which has a cache line of 32 bytes, the worst case search time was found to be 970 nsec, using M=64 and p=16.

VIII. CONCLUSION

We have described a basic binary search scheme for the best matching prefix problem. Basic binary search requires two new ideas: encoding a prefix as the start and end of a range, and precomputing the best matching prefix associ­ated with a range. Then we have presented three crucial enhancements: use of an initial array as a front end, mul­tiway search, and multicolumn search of identifiers with large lengths.

We have shown how using an initial precomputed 16 bit array can reduce the number of required memory ac­cesses from 16 to 9 in a typical database; we expect sim­ilar improvements in other databases. We then presented the multiway search technique which exploits the fact that most processors prefetch an entire cache line when doing a memory access. A 6 way branching search leads to a worst case of 5 cache line fills in a Pentium Pro which has a 32 byte cache line. We presented measurements for IPv4. Using a typical database of over 30,000 prefixes we obtain a worst case time of 490 nsec and an average time of 130 nsec using storage of 0.7 Mbytes. We believe these are very competitive numbers especially considering the small

storage needs.

For IPv6 and other long addresses, we introduced mul­ticolumn search that avoided the multiplicative factor of W/M inherent in basic binary search by doing binary search in columns of M bits, and moving between columns using precomputed information. We have estimated that this scheme potentially has a worst case of 7 cache line fills for a database with over 50000 IPv6 prefixes database.

For future work, we are considering the problem of using different number of bits in each column of the multicolumn search . We are also considering the possibility of laying out the search structure to make use of the page mode load to the L2 cache by prefetching. We are also trying to retrofit our Pentium Pro with an SDRAM or RDRAM to improve cache loading performance; this should allow us to obtain better measured performance.

REFERENCES

[Asc]            Ascend. Ascend GRF IP Switch Frequently Asked Ques‑
tions. http://www.ascend.com/299.html#15.

[BCDP97] Andrej Brodnik, Svante Carlsson, Mikael Degermark, and Stephen Pink. Small Forwarding Table for Fast Rout­ingLookups. To appear in ACM Sigcomm'97, September 1997.

[HP96] Hennessey and Patterson. Computer Architecture A quantitative approach, 2nd Edn. Morgan Kaufmann Pub­lishers Inc , 1996.

[Inta]            Intel. Intel Architecture Software developer's Manual,

Vol              1:                           Basic             Architecture.
http://www.intel.com/design/litcentr/litweb/pro.htm.

[Intb]            Intel. Pentium Pro. http://pentium.intel.com/.

[Mer]            Merit. Routing table snapshot on 14 Jan 1997 at the

Mae-East NAP. ftp://ftp.merit.edu/statistics/ipma. [Mic]  Micron.   Micron    Technology           Inc.

http://www.micron.com/.

[MTW95]    Anthony J. Bloomfeld NJ McAuley, Paul F. Lake Hopat‑
cong NJ Tsuchiya, and Daniel V. Rockaway Township

Morris County NJ Wilson.    Fast Multilevel heirarchical

routing table using content-addressable memory. U.S. Patent serial number 034444. Assignee Bell Communica­tions research Inc Livingston NJ, January 1995.

[NMH97] Peter Newman, Greg Minshall, and Larry Huston. IP Switching and Gigabit Routers. IEEE Communications Magazine, January 1997.

[oT]             McGray Massachussetts Institute of Technology. Internet

Growth                                                                 Summary.
http://www.mit.edu/people/mkgray/net/internet­growth-summary.html.

[Per92]        Radia Perlman. Interconnections, Bridges and Routers.
Addison-Wesley, 1992.

[PZ92]         Tong-Bi Pei and Charles Zukowski. Putting Routing Ta‑
bles in Silicon. IEEE Network Magazine, January 1992.

[Ram]        Rambus. Rdram. http://www.rambus.com/.

[Sim]           SimpleTech.                     Simple     Technology        Inc.
http://www.simpletech.com/.

[Skl] Keith Sklower. A Tree-Based Routing Table for Berkeley Unix. Technical report, University of California, Berke­ley.

[SW95] W. Richard Stevens and Gary R Wright. TCP/IP Illus­trated, Volume 2 The Implementation. Addison-Wesley, 1995.

[WVTP97] Marcel Waldvogel, George Varghese, Jon Turner, and Bernhard Plattner. Scalable High Speed IP Routing Lookups. To appear in ACM Sigcomm'97, September 1997.