This document was made by OCR from a scan of the technical report. It has not been edited or proofread and is not meant for human consumption, but only for search engines. To see the scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL that got you here.

Chapter 1

Implementing Coherent Memory

Butler W. Lampson

In the design of a shared-memory multiprocessor, there is a conflict between the need for a coherent memory in which every write done by one processor is immediately visible to all the others, and the fact that a memory read or write that uses only a cache local to the processor can be done more quickly than one that communicates with a global memory or another processor. Coherent memory is good because we know how to program with it; the incoherent memory that results from minimizing communication is good because it is fast.

In this paper we show how to write precise specifications for coherent and incoherent memory, and how to implement coherent memory in several ways, one of which is on top of incoherent memory. Our technique for showing the correctness of the implementations is the abstraction function introduced by Hoare [8] to handle abstract data types. A decade later, Lamport [1] and Lynch [10] extended Hoare's methods to concurrent systems like the ones we treat.

We begin by giving a careful specification for the coherent memory S that we really want; it is just a function from addresses to data values. We also specify an incoherent memory T that has fast implementations. After a brief explanation of what it means to implement a specification and how to prove the correctness of an implementation using abstraction functions, we explore how to change T so that it implements coherent memory with as little communication as possible. Our first step is a simple idealized implementation U derived from T by strengthening the guards. Unfortunately U is extremely non-local and therefore impractical. We describe two ways to make U local enough to be practical. Both are based on the idea of using locks on memory locations.

First we show how to use reader/writer locks to get a practical version of U called a coherent cache. We do this in two stages: an ideal cache B and a concrete cache C. The cache changes the guards on internal actions of T as well as on the external read and write actions, so it can't be implemented simply by adding a test before each read or write of T, but instead requires changes to the insides of T. We complete our treatment of caches by sketching several implementations of

C that are used in commercial multiprocessors.

Then we show how to use locks in a different way to get another practical version of U, called E. The advantage of E is that the locking is separate from the internal actions of the memory system, and hence E can be implemented entirely in software on top of an incoherent memory system that only implements T. In other words, E is a practical way to program coherent memory on a machine whose hardware provides only incoherent memory.

All our implementations make use of a global memory that is modelled as a function from addresses to data values; in other words, the specification for the global memory is simply S. This means that an actual implementation may have a recursive structure, in which the top-level implementation of S using one of our algorithms contains a global memory that is implemented with another algorithm and contains another global memory, etc. This recursion terminates only when we lose interest in another level of virtualization. For example,

a processor's memory may be made up of a first level cache plus

a global memory made up of a second level cache plus

a global memory made up of a main memory plus

a global memory made up of a local swapping disk plus

a global memory made up of a file server ....

1.0.1 Notation

We write our specifications and implementations using state machines [9]. As usual, a state machine consists of

· a state space, which we represent by the values of a set of named variables,

· a set of initial states, and

· a set of transitions or actions. Each action consists of:

- a name, which may include some parameters,

- a guard, a predicate on the state that must be true for the action to happen, and

- a state change, which we represent by a set of assignments of new values to the state variables.

We write an action in the form

name guard - state change

Actions are atomic: each action completes before the next one is started. To express concurrency we introduce more actions. Some of these actions may be internal, that is, they may not involve any interaction with the client of the memory. Internal actions usually make the state machine non-deterministic, since they can happen whenever their guards are satisfied, unlike external actions which require some interaction with the environment.

To make our state machines easier to understand we give types for the variables, either scalar or function types. We also give names to some state functions on the variables. For instance, we define clean (V p. newp) and then use clean in expressions exactly like a variable. Finally, we write down useful invariants of each state machine, predicates that are true in every reachable state.

1.1 S: Coherent Memory Specification

This is just what you expect. The memory is modeled as a function m from addresses to data values, and the Read and Write actions give direct access to the function. We write the spec in this rather fussy form only for compatibility with the more complicated versions that follow. The actions take a processor p as a parameter so that they have the same names as the Read and Write actions of later systems, but in this spec they don't depend on p.

type

A Address

D Data

P Processor variable

m : A -+ D Memory

action

Read(p,a,vard) d : m(a)

Write(p,a,d) m(a) : d

From now on we reduce clutter in the text of the specs by:

· Dealing only with one address, dropping the a argument everywhere.

· Writing the p argument as a subscript.

With these conventions, the actions above look like this:

action

Readp(var d) d : m

Writ ep(d) m : d

1.2 T: Incoherent Memory Specification

The idea of incoherent memory is that in addition to a global memory m^ there is a private view v _p for each processor; it contains data values for some subset of the addresses. Here is the state of T:

		FromVb(1)			ToVa (1)
	x y			x kz			x z
	m^			m^			m^
x	nil	x	x	nil	x	x	nil	x
nil	z*	y	nil	z	y	kz	z	y
va	vb	vc	va	vb	vc	va	vb	vc

Figure 1.1 Some possible transitions of T with three processors

variable

m^ :A-+D

v :P-+A-+(D j nil)

new :P-+A-+Bool

state function

liver (vr =6nil)

invariant

newr liver

Processor p uses vr to do its Readr and Writer actions. Internal actions ToV _r and FromV _r copy data back and forth between p's view and the global memory ^m. An address is live in p if p's view has a value for it. To do a Readr a processor may have to wait for an ToV _r to make the address live; a processor can do a Writer at any time. Each view also keeps track in new of the addresses for which it has new data that hasn't yet been copied to ^m. An internal Drop _r action removes a datum that isn't new from p's view. An external Barrier _r action waits until an address is not live; this ensures that the value written by any earlier Write has been copied to m^ and that any later Read sees a value from ^m.

There are commercial machines whose memory systems have essentially this specification [3]. Others have explored similar specifications [4, 5].

Figure 1 is a simple example which shows the contents of two addresses 0 and 1 in m^ and in three processors a, b, and c. A new value is marked with a , and circles mark values that have changed. Initially Readb(1) yields the new value z, Readc(1) yields y, and Reada(1) blocks because va(1) is nil. After the FromVb the global location ^m(1) has been updated with z. After the ToVa, Reada(1) yields z. One way to ensure that the FromVb and ToVa actions happen before the Reada(1) is to do Barrierb followed by Barriera between the Writeb(1) that makes z new in vb and the Reada(1).

Here are the possible transitions of T for a given address:

: live __________________ live A new

~

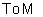
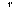H Drop

H

H

W rite Write

H

H

H

H

H

H

H j

live A new

Finally, here are the actions of the specification for incoherent memory:

action

Read_t,(var d) live_t, - d : vt,

Writ e_t,(d) vt, : d, newt, : true

Barrier_t, :live_t, - skip

internal action

To Vt, : newt, - v t, : m^

From Vt, newt, - m^ : vt,, newt, : false

Drop _t, : newt, - v t, : nil

After a Barrier_t,, v _t, is guaranteed to agree with m^ until the next time m^ changes.¹

Note that in general a ToV action is needed to establish the guard on Read, and a Drop action to establish the guard on Barrier. This means that an implementation will do something that has the effect of ToV when it's trying to do a Read, and similarly for Drop and Write. A Drop in turn may require a From V to establish its guard.

This is the weakest shared-memory spec that seems likely to be useful in practice. But perhaps it is too weak. Why do we introduce this messy incoherent memory T? Wouldn't we be much better off with the simple and familiar coherent memory S? There are two reasons to prefer T to S.

1. An implementation of T can run faster—there is more locality and less communication. As we will see in implementation E, software can batch the communication that is needed to make a coherent memory out of E.

2. Even S is tricky to use when there are concurrent clients. Experience has shown that it's necessary to have wizards to package it so that ordinary programmers can use it safely. This packaging takes the form of rules for writing concurrent programs, and procedures that encapsulate references to shared memory. The two most common examples are:

• Mutual exclusion / critical sections / monitors, which ensure that a number of references to shared memory can be done without interference, just as in a sequential program. Reader/writer locks are an important variation.

'An alternative version of Barrier has the guard liver V (vr ^m); this is equivalent to the current Barrier followed by an optional ToV r. You might think that it's better because it avoids a copy from m^ to v _r in case they already agree. But this is a spec, not an implementation, and the change doesn't affect its external behavior.

· Producer-consumer buffers.

For the ordinary programmer only the simplicity of the package is important, not the subtlety of its implementation. As we shall see, we need a smarter wizard to package T, but the result is as simple to use as the packaged S. The implementation E below shows how to use T to obtain critical sections.

1.2.1 Specifying legal histories directly

It's common in the literature to write the specifications S and T explicitly in terms of legal sequences of references at each processor, rather than as state machines [3, 4]. We digress briefly to explain this approach.

For S, there must be a total ordering of the Readp(a, d) or Writ ep(a, d) actions done by the processors that

· respects the order at each p, and

· such that for each Readp(a, d) and latest preceding Writ ep(a, d^'), d d^'.

For T, there must be a total ordering of the Readp(a, d), Writep(a, d), and Barrierp(a) actions done by the processors that

· respects the order of Readp(a, -), Writ ep(a, -), and Barrierp(a) at each p for each a, and

· such that Read reads the data written by the latest preceding Write, as in S.

The T spec is weaker than S because it allows references to different addresses to be ordered differently. Usually the barrier operation actually provided does a Barrier for every address, and thus forces all the references preceding it at a given processor to precede all the references following it.

It's not hard to show that these specs written in terms of ordering are almost equivalent to S and T. Actually they are somewhat more permissive. For example, the T spec allows the following history

· Initially x 1,y 1.

· Processor a reads 4 from x, then writes 8 to y.

· Processor b reads 8 from y, then writes 4 to x.

We can rule out this kind of predicting the future by observing that the processors make their references in some total order in real time, and requiring that a suitable ordering exist for the references in each prefix of this real time order, not just for the entire set of references. With this restriction, the two versions of the T spec are equivalent.

1.3 Implementations

Having seen the specs for coherent and incoherent memory, we are ready to study some implementations. We begin with a precise statement of what it means for an implementation Y to satisfy a specification X [1, 10].

X and Y are state machines. We partition their actions into external and internal actions. A history of a machine M is a sequence of actions that M can take starting in an initial state, and an external history of M is the subsequence of a history that contains only the external actions.

We say Y implements X if every external history of Y is an external history of X.² This expresses the idea that what it means for Y to implement X is that the externally observable behavior of Y is a subset of the externally observable behavior of X; thus you can't tell by observing Y that you are not observing X.

The set of all external histories is a rather complicated object and difficult to reason about. Fortunately, there is a general method for proving that Y implements X without reasoning explicitly about histories in each case. It works as follows. First, define an abstraction function f from the state of Y to the state of X. Then show that Y simulates X:

1. f maps an initial state of Y to an initial state of X.

2. For each Y-action and each state y there is a sequence of X-actions that is the same externally, such that the diagram below commutes.

f(y)

X-actions

f(y^,)

A sequence of X-actions is the same externally as a Y-action if they are the same after all internal actions are discarded. So if the Y-action is internal, all the X-actions must be internal (there might be none at all). If the Y-action is external, all the X-actions must be internal except one, which must be the same as the Y-action.

Then by a straightforward induction Y implements X, because for any Y-history we can construct an X-history that is the same externally, by using (2) to map each Y-action into a sequence of X-actions that is the same externally. Then the

²Actually this definition only deals with the implementation of safety properties. Roughly speaking, a safety property is an assertion that nothing bad happens; it is a generalization of the notion of partial correctness for sequential programs. Specifications may also include liveness properties, which roughly assert that something good eventually happens; these generalize the notion of termination for sequential programs [1]. Liveness is beyond the scope of this paper.

sequence of Y-actions will be the same externally as the corresponding sequence of X-actions.

In order to prove that Y simulates X we usually need to know what the reachable states of Y are, because it won't be true that every action of Y from an arbitrary state of Y simulates a sequence of X actions. The most convenient way to characterize the reachable states of Y is by an invariant, a predicate that is true of every reachable state. Often it's helpful to write the invariant as a conjunction, and to refer to each conjunct as an invariant.

So the structure of a proof goes like this:

· Establish invariants to characterize the reachable states, by showing that the invariants are true in each initial state and that each action maintains the invariants.

· Define an abstraction function.

· Establish the simulation, by showing that each Y action simulates a sequence of X actions that is the same externally.

This method works only with actions and does not require any reasoning about histories. Furthermore, it deals with each action independently; only the invariants connect the actions. So if we change (or add) an action, we only need to verify that the new action maintains the invariants and simulates a sequence of S-actions that is the same externally. In particular, strengthening a guard preserves the "implements" relation. We will exploit this observation to evolve an obviously correct implementation of S into some more efficient ones.

In what follows we give only the abstraction function and the invariants; the actual proofs of invariants and simulations are routine.

1.4 U: An impractical implementation of S

We begin by giving an implementation called U which is identical to T except that some of the guards are stronger, in fact, strong enough that U implements S. Therefore there's no need for Barrier in U. Unfortunately, U can't be directly implemented itself because a practical implementation must look only at local state, and U has variables curp and clean that are not local. However, U is easy to understand, and it gives us a basis from which to develop a number of different implementations that are practical.

For the sake of brevity, in describing U we leave out most of the actions that are the same in T. In order to make it easy for the reader to compare T and U, we mark the changes by striking out text that is only in T and boxing text that is only in U.

For this and all our other implementations of S, we use the same abstraction function:

m if clean then m^ else (v _r for some p such that newr)

This is only well-defined if vr is the same for every p for which newr true. All of our implementations maintain the invariant that new _r is exclusive, that is, true for at most one p, which ensures that the abstraction function is well-defined.

variable

m^ :A-+D

v :P-+A-+(D j nil)

new :P-+A-+Bool

state function

liver (vr 6 nil)

curr (vr m)

clean 8p. newr

invariant

newr liver

new is exclusive, that is, it's true for at most one processor

action

Readr(vard) liver cur _r -+ d: vr

Barrier is uninteresting because every p is always current when it does a Read.

U implements S because:

· new is exclusive, so m is well-defined;

· Read returns m as required, Write changes m as required;

· Other actions leave m unchanged.

1.5 B and C: A cache implementation of U

We take two steps to get from U to a generic cache implementation. The first step is B, which still uses non-local state functions clean and onlyr, but gets rid of curr by maintaining a new invariant, liver,' cur _r and strengthening the guard on Read from cur _r to liver. To maintain the new invariant we also need to strengthen the guards on Writer and ToV r.

variable

m^ :A-+D

vr :A-+(D j nil)

new _r : A -+ Bool

state function

liver (v _r 6 nil)

curr vr m)

clean Vp. newr

onlyr V q 6 p . : liveq

invariant

newr liver

new is exclusive

liver curr
action Readr(var d) curr
		liver	— d: vr
Writer(d) cleanVnewr	onlyr		— vr : d,newr : true

internal action

To Vr : n ewr clean — vr : m^

. . .

As in U, Barrier is uninteresting because every p is always current when it does a Read.

Now we can give C, a practical implementation of Read, Write, and ToV which pushes the non-locality into an action Acquire that acquires a write lock, and the state function free. The invariants imply that the new guards are as strong as the old ones.

variable

m^ :A—D

v :P—A—(D j nil)

new :P—A—Bool

lock : P— A — Bool

state function

liver (vr6 nil)

curr (vr m)

clean Vp. newr

onlyr V q 6 p . : liveq

free Vp. ilockr

invariant

newr liver

new is exclusive

liver curr

newr lockr

lockr onlyr
lock is exclusive

action			Implementing Coherent Memory 11
Readr(var d)	liver		— d :	vr
Writer(d) internal action	only	lockr	— vr :	d,newr :	true
	r
ToVr		: new r A (lockrV free)	— v r :	m^
	clean

. . .

Acquirer free A onlyr — lockr : true

Releaser : new _r — lockr : false

1.5.1 Implementing Acquire

Now all we have to do is implement the guard of Acquire. To establish free A onlyr, we need:

· a way to test it, and

· a way to progress toward it by suitable Releaser and Drop _r operations.

There are three general approaches to solving these problems. All three have been used in commercial multiprocessors [2, 7].

1. Directory, usually in conjunction with a switch-based processor-memory interconnect [11]:

· Keep centrally a set {p : liver V lockr} for each address or set of addresses or "cache block". Usually this directory information is kept with the m^ data.

· Ask each p that holds data or a lock to give it up (by doing Drop _r or Releaser) in order to ensure progress.

2. Snoopy, usually in conjunction with a bus-based processor-memory interconnect [6]:

· If you don't hold the necessary lock, broadcast a request for progress to all processors.

· Each processor q responds with the value of lockq; "or" all the responses, often using a "wired-or" electrical signalling scheme.

3. Hierarchical, which handles problems of scale by subdividing the problem; either method (1) or method (2) can be used at each level of the hierarchy:

· Partition the p's into pSets

· Keep liv _er8 and lockr₈ variables for each pSet

· Maintain V liver ' liv _er5 and V lockr 'lockr₅.

rEr5 rEr5

· Deal with each pSet separately. Use any of (1)-(3) to handle each pSet and to handle the set of pSets. It's not necessary to use the same method in each case.

1.5.2 Update protocols

There is a popular variation of the caches described by B and C called an "update protocol". It allows data to be copied directly from one cache to another without going through m^ . Here is B-update; it simply adds one action to B.

internal action

VtoVrq liveq -+ vr : vq

VtoVrq maintains the invariants because of the invariant liver ' curr, and it doesn't change m.

And here is C-update; we mark the changes from C, except that we show how the guards of ToV and VtoV are changed from B-update. The invariant is weaker than C's, and the guards on ToV correspondingly stronger. The idea is that p can release the lock, so that copies are allowed in other processors' views, without updating m^ and making new _r false. So the guard on ToV is quite non-local, and only a snoopy implementation is attractive. Actual implementations usually broadcast writes to shared locations; this corresponds to doing Dropq; Writer; VtoVrq more or less atomically, and ensuring this atomicity can be tricky.

invariant

new _r ' lockr

action

ToVr clean A free

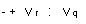VtoVrq liveq A free

1.6 E: Programming with incoherent memory

Now for a different modification of U that gets us to a different practical implementation, similar to C but not identical. We call this E, and we show changes from U by the outer boxes and strikeouts, and the differences from C inside. The latter are:

· The invariant relating live and cur is weaker:

— C: live ' cur

— E: live A lock ' cur

This is the crucial difference.

· Read has a stronger guard that includes a lock conjunct.

· ToV has a weaker guard, just new without the lock V free conjunct.

· Acquire has a weaker guard without only; in fact, E doesn't use only at all.

· Acquire and Release have added Barrier actions.

The critical difference between E and C is that the internal actions of E are the same as those of T. This means that we can use an unmodified T as the basis of E. The Read and Write actions of E are the Read and Write actions of T preceded by tests that lock is true. Usually this is done by confining all occurrences of Read and Write to critical sections within which lock is known to be true. The Acquire and Release operations are done at the start and end of a critical section in the usual way. In other words, E shows how to build coherent memory on top of incoherent memory.

Note: it's not actually necessary for Acquire and Release to be fully atomic; the Barriers can be done separately.

variable

m^ :A—+D

v :P—+A—+(D j nil)

new :P—+A—+Bool

lock : P—+ A —+ Bool

state function

live,_? (v,? 6nil)

cur,? (v,? ^m)

clean Vp. new,?

only,_? V q 6 p . : liveq

free ~ V p. lock,_?

invariant

new,? 'live,_?
new is exclusive

live,_? A lock,_? ' cur,?

new,? 'lock,_?

lock,_? ' only,_?

lock is exclusive

action

Read,_?(var d) cur,?

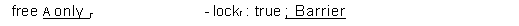
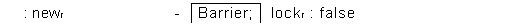We have written E with an exclusive lock, which is the most common way to do critical sections. It works just as well with reader/writer locks; the guard for Read is rlock _r A liver, the guard for Write is wlockr, and there are separate Acquire and Release actions for the two kinds of locks.

1.6.1 Remarks

The T spec allows a multiprocessor shared memory to respond to Read and Write actions without any interprocessor communication. Furthermore, these actions only require communication between a processor and the global memory when a processor reads from an address that isn't in its view. The expensive operation in this spec is Barrier, since the sequence Writea; Barriera; Barrierb; Readb requires the value written by a to be communicated to b. In current implementations Barrier _r is even more expensive because it acts on all addresses at once. This means that roughly speaking there must be at least enough communication to record globally every address that p wrote before the Barrier _r and to drop from p's view every address that is globally recorded as new.

Although this isn't strictly necessary, all current implementations have additional external actions that make it easier to program mutual exclusion. These usually take the form of some kind of atomic read-modify-write operation, for example an atomic swap of a register value and a memory value. A currently popular scheme is two actions: ReadLinked(a) and WriteConditional(a), with the property that if any other processor writes to a between a ReadLinkedr(a) and the next WriteConditionalr(a), the WriteConditional leaves the memory unchanged and returns a failure indication. The effect is that once the WriteConditional succeeds, the entire sequence is an atomic read-modify-write from the viewpoint of another processor [3]. Of course these operations also incur communication costs, at least if the address a is shared.

We have shown that a program that touches shared memory only inside a critical section cannot distinguish memory that satisfies T from memory that satisfies the serial specification S. This is not the only way to use T, however. It is possible to program other standard idioms, such as producer-consumer buffers, without relying on mutual exclusion. We leave these progams as an exercise for the reader.

1.7 Conclusion

The lesson of this paper is twofold:

· It is possible to give simple but precise specifications for several kinds of shared memory that do not depend on the intended implementations. Furthermore, the essential ideas of the implementations can also be described precisely, and it is fairly straightforward to prove that the implementations satisfy the specifications. Standard methods for reasoning about concurrent programs and their specifications work very well.

· Techniques for implementing serial shared memory have much more in common than you might think, even though they may use very different combinations of hardware and software to realize the common idea.

References

[1] Abadi, M. and Lamport, L., The existence of refinement mappings, Theoretical Computer Science 82 (2), 1991, 253-284.

[2] Archibald, J. and Baer, J-L., Cache coherence protocols: Evaluation using a multiprocessor simulation model, ACM Trans. Computer Systems 4 (4), Nov. 1986, 273-298.

[3] Digital Equipment Corporation, Alpha Architecture Handbook, 1992.

[4] Gharachorloo, K., et al., Memory consistency and event ordering in scalable shared-memory multiprocessors, Proc. 17th Symposium on Computer Architecture, 1990, 15-26.

[5] Gibbons, P. and Merritt, M., Specifying nonblocking shared memories, Proc. 4th ACM Symposium on Parallel Algorithms and Architectures, 1992, 158-168.

[6] Goodman, J., Using cache memory to reduce processor-memory traffic. Proc. 10th Symposium on Computer Architecture, 1983, 124-131.

[7] Hennessy, J. and Patterson, D., Computer Architecture: A Quantitative Approach, Morgan Kaufann, 1990.

[8] Hoare, C. A. R., Proof of Correctness of Data Representation, Acta Informatica 4, 1972, 27 1-28 1.

[9] Lamport, L., A simple approach to specifying concurrent systems, Communications of the ACM, 32 (1), 1989, 32-47.

[10] Lynch, N. and Tuttle, M., Hierarchical correctness proofs for distributed algorithms, Proc. ACM Symposium on Principles of Distributed Computing, 1987, 137-151.

[11] Tang, C., Cache system design in the tightly coupled multiprocessor system. Proc. AFIPS National Computer Conference, 1976, 749-753.