This document was made by OCR
from a scan of the technical report. It has not been edited or proofread and is
not meant for human consumption, but only for search engines. To see the
scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL
that got you here.
Correctness of At-Most-Once
Message Delivery Protocols
Butler W. Lampsona,
Nancy A. Lynchb and Jørgen F. Søgaard~Andersenc* aCambridge Research Laboratory,
DEC, Cambridge, MA 02139, USA.
bLab. for Computer Science, MIT,
545 Tech. Square, Cambridge, MA 02139, USA.
cDepartment of Computer
Science, Technical University of Denmark, Building 344, DK-2800
Lyngby, Denmark.
This paper addresses the issues of formal
description and verification for communication protocols. Specifically, we present the results of a project concerned
with proving correctness of two
different solutions to the at-most-once message delivery problem. The two
implementations are the well-known five-packet handshake protocol and a
timing-based protocol developed for networks with bounded message
delays.
We use an operational
automaton-based approach to formal specification of the problem statement and
the implementations, plus intermediate levels of abstraction in a step-wise
development from specification to implementations. We use
simulation techniques for proving correctness.
In the project we deal with safety, timing, and
liveness properties. In this paper, however, we concentrate on safety
and timing properties.
Keyword Codes: C.2.2; D.2.4; F.1.1
Keywords:
Computer Systems Organization, Network Protocols; Software, Program Verification;
Theory of Computation, Models of Computation
1. INTRODUCTION
During the past few years,
the technology for formal verification of communication protocols has matured to the point where we believe that
it now provides practical assistance for protocol design and validation.
Recent advances include the development of formal models that allow reasoning
about timed systems as well as untimed systems, e.g., [2, 5, 13], and the
development of simulation techniques (including refinement mappings and forward and backward simulations) for proving that
one protocol implements another, e.g., [1, 5-7, 13]. In this paper, we show how
these techniques can be used to verify an important class of
communication protocols - those for at-most-once
message delivery. The goals of our project are
twofold: to provide better understanding, documentation and proof for these
protocols, and to test the adequacy of the models and proof techniques.
The at-most-once message delivery problem is that of delivering a sequence of messages submitted
by a user at one location to a user at another location. Ideally, we would like
to insist that all messages be delivered in
the order in which they are sent, each exactly once, and that an acknowledgement
be returned for each delivered message.'
 eResearch supported in
part by the Danish Research Academy.
eResearch supported in
part by the Danish Research Academy.
1 Our
definition of at-most-once message delivery is different from what some people
call at-most-once message delivery in that we include acknowledgements
and require messages to be delivered in order.
Unfortunately, it is
expensive to achieve these goals in the presence of failures (e.g., node crashes and timing anomalies). In fact, it is
impossible to achieve them at all unless some change is made to the stable
state (i.e., the state that survives a crash) each time a message is delivered.
To permit less expensive solutions, we weaken the statement of the problem slightly. We allow some messages to be lost when
a node crash occurs; however, no messages should
otherwise be lost, and those messages that are delivered should not be reordered or duplicated. (The specification is weakened
in this way because message loss is
generally considered to be less damaging than duplicate delivery.) Now it is required
that the user receive either an acknowledgement
that the message has been delivered, or in the case of crashes, an
indication that the message might have been lost.
There are various ways to solve the at-most-once
message delivery problem. All are based on
the idea of tagging a message with an identifier and transmitting it repeatedly
to overcome the unreliability of the channel. The
receiver2 keeps a stock of "good" identifiers that it has never accepted before; when it
sees a message tagged with a good identifier,
it accepts it, delivers it, and removes that identifier from the set.
Otherwise, the receiver just discards the message, perhaps
after acknowledging it. Different protocols use
different methods to keep the sender and the receiver more or less in agreement
about what identifiers to use.
A desirable property, which is not directly
related to correctness, is that the implementations
offer a way of cleaning up "old" information when this cannot affect
the future behavior.
In this work, we consider two protocols that are
important in practice: the clock-based protocol of Liskov, Shrira and
Wroclawski [10] and the five-packet handshake protocol of Belsnes [3]. The latter is the standard protocol for
setting up network connections, used in TCP, ISO TP-4, and many other transport
protocols. It is sometimes called the three-way
handshake, because only three packets are needed for message delivery; the
additional packets are required for acknowledgement and
cleaning up the state. The former protocol was developed as an example to show
the usefulness of clocks in network protocols [9] and has been implemented at M.I.T. Both protocols are
sufficiently complicated that formal specification and proof seems
useful.
The basic model we use is based on the (timed) automaton model of
Lynch and Vaandrager [13] with an extra added
component to express liveness [5]. We express both protocols, as well as the formal specification of the at-most-once
message delivery problem, in terms of this
model. In the project we carry out complete correctness proofs for both
protocols. Some highlights of our proofs are as follows:
Although
the two protocols appear to be quite different, we have found that both can be
expressed formally as implementations of a common generic protocol C, which, in turn, is an implementation of the problem specification. To prove that C implements the specification,
for proof-technical reasons we introduce an additional level of abstraction,
the delayed-decision
specification D. This is
depicted in Figure 1. Introducing intermediate levels of abstraction, like C and D, is a general proof strategy that allows large,
 2We denote by "receiver" the protocol entity that is situated
on the receiver node, and use phrases like "the
user at the receiver end" to denote the user that communicates with the
receiver. Correspondingly for "sender".
2We denote by "receiver" the protocol entity that is situated
on the receiver node, and use phrases like "the
user at the receiver end" to denote the user that communicates with the
receiver. Correspondingly for "sender".
|
S
|
Specification
Delayed-Decision
Specification
Generic
Protocol
|
|
~
|
|
D
|
|
~
|
|
C
|
V~V V ' ' '?
|
Clock-Based Protocol
|
C
|
|
H
|
Five-Packet Handshake Protocol
|
Figure 1. Overview of the levels of abstraction in our work.
complicated proofs to be split into smaller and more managerable
subproofs.
The proof that an implementation correctly
implements a specification is divided into two parts.
First, a simulation technique is applied to show that the implementation safely implements the
specification, i.e., that all safety (and timing) properties of the implementation are allowed by the specification. Then,
heavily based on the simulation result, we prove liveness
properties, and thus, correctness.
As proof techniques we use a backward simulation
to show that D safely implements the
specification, and forward simulations to show that each of the two protocols
safely implements C and that C safely implements D. Because of space limitations,
we only treat safe implementation in this paper. Our intention with this paper
is to give an overview of our work and to
convey our experiences with specifying and verifying practical communication protocols. For this reason we have
left out many formal details. We refer to
our full report [8] for such details. The full report also contains an
exhaustive treatment of liveness properties of the protocols.
The rest of the paper is organized as follows. We
start in Section 2 by giving an introduction to our model. Then in Sections 3
and 4 we present the problem specification and the
low-level protocol C. In this paper we will only briefly deal with the H protocol. In Section 5 we show how aspects of both low-level protocols
can be captured in the generic protocol C, and in Section 6 we outline the correctness
proofs. In doing so we present the delayed-decision specification D.
Finally, we give concluding remarks in Section 7.
2. THE
UNDERLYING THEORY
The general model we use to specify safety and timing properties at all
levels of abstraction is based on the (timed) automaton model of [5, 13] and the I/O automaton model of [11, 12]. An automaton is a state machine with named actions associated
with its transitions. Thus, an automaton consists of
· a (possibly infinite) set of states. In timed systems a now component indicates
the time,
·
a (nonempty) set of start states,
·
a set of actions partitioned into visible actions (which are furthermore partitioned into input actions and output actions),
internal actions (which are invisible from the environment of the
system), and, for timed systems, a special time-passage action, and
·
a
transition relation of ((pre-)state, action, (post-)state) triples. Each triple
is called a step.
For timed systems, the steps involving the
time-passage action have to satisfy certain axioms that give natural properties
of real time, e.g., that time cannot go backwards.
Correctness
of an automaton is specified in terms of its external behavior given by the set of traces, each of
which consists of a sequence of visible actions that the automaton can perform. In timed systems these actions are
furthermore paired with their time of occurrence to form timed traces. One
automaton, A,
safely implements another
automaton, B, if the set of (timed) traces of A
is included in that of B.
The papers [6, 13, 5] present a collection of simulation proof
techniques (refinement mappings, forward and
backward simulations, etc.) for showing that one (timed) automaton safely implements another. Each of these techniques
involves describing a relation between the states of
an implementation automaton and those of a specification automaton. Each technique requires a particular type of
correspondence between initial states of the
two automata, as well as a particular type of correspondence between their
steps. Figure 2 illustrates how each step of the
implementation automaton must correspond to a (possibly
empty) sequence of steps of the specification automaton containing exactly the
same visible actions.
The main
distinction between forward and backward simulations, which are abstract representations of history [16]
and prophecy [1] variables, respectively, lies in the way these corresponding sequences of steps of the
specification are found given a step of the implementation: in a forward simulation it must be shown that from each state of the specification which is related to the pre-state of the step of the
implementation, there exists a
sequence of steps (with the right actions) ending in some state of the specification which is related to the post-state of the step of the specification.
Thus, one must, for all states
related to the pre-state, trace forward to
find some state related to the post-state. Conversely, in a backward simulation
one must, for all states related to the post-state, trace backward to
find some state related to the pre-state. A refinement mapping is a forward simulation where the
relation is a function.
Since we only have to consider the steps of the
implementation automaton which start in a
reachable state, we will usually prove some invariants, i.e., properties that are
true of all the reachable states, to restrict the states that we need to
consider.
More
formally, let A and B be
automata and let R be a relation over the states
of A and the states of B. Then R is a forward simulation from A
to B
if
·
For each start state of A, there is a related (by R) start state of B.
|
Specification Level .------
|
a b
. .
~ ~
|
. . . c c c
~ ~ ~
|
|
~
|
|
~
EEU
|
|
~
|
EEU ~
|
|
|
Simulation Relation
|
|
|
|
|
|
|
|
Implementation Level .
|
|
E
EL ~
. .
~ ~
|
b
|
~ . ~
|
EEL ~
. .
~ ~
|
c c c
|
Figure 2. Example of a simulation. The actions a and b are visible actions. The rest
of the transitions are thought of as labelled by internal actions.
q
For each step (s,
a, s')
of A,
where s
and s' satisfy the invariants of A,
and each state
u related to s that
satisfies the invariants of B, there exists a
sequence of steps of B, starting in u and ending in some state
related to s', such that
the sequence of steps contains the same visible
actions as (s, a, s').
For timed systems the now components and
time-passage actions require additional treatment. A backward
simulation can be defined similarly.
Inductive proofs show the soundness of the
simulation proof techniques, i.e., that they imply
safe implementation. However, not all techniques are complete, meaning
that for some of the simulation techniques, e.g., forward
and backward simulations, safe implementation
does not imply the existence of such a simulation. Also, different simulation techniques apply to different situations. Thus, although
a forward simulation is the most intuitive technique, there are some situations
that require other techniques, like backward simulations.
For instance, a backward, but not a forward, simulation can be used in situations where the implementation makes some decisions
later than the corresponding decisions are made in
the specification. We will see an example of this in Section 6.
3. SPECIFICATION S
This section is devoted to giving the specification, called S, of the at-most-once message delivery problem more formally. Since this is an untimed specification, we give the specification
in terms of an untimed automaton.
Figure 3 shows the user-interface of the protocols to be developed by
depicting the specification as a
"black box" with visible input and output actions. A user can send a message m by
performing a send
msg(m) action and the protocol can deliver the next message m by
performing a receive
msg(m) action. A Boolean acknowledgement b is passed to the user at the sender side by an ack(b) action. At both the sender and receiver sides, a crash action causes the protocol to enter a recovery phase
where messages might be lost
(modelled by an internal lose action). A recover action, at the side where the crash occurred, then signals the end of the
recovery phase, after which no messages can be lost unless
new crashes occur.
The following code describes the specification S in a simple
precondition-effect style commonly used for
I/O-automata protocols [11, 12]. Note that input actions have no precon‑
Specification 6
|
~ !!!!!~!
Sender Side
!!!!!!~
|
send msg(m)
|
|
receive msg (m)
|
Receiver Side
|
|
~
ack(b)
|
~
I crashr
|
|
I
crashV ~
|
|
recover,
|
|
recoverr
|
|
|
I
|
|
|
~
|
Figure 3. The specification 6
as a "black box"
ditions since our system should be able to respond to
input from the environment at any time.
The state
of the automaton contains a queue of pending messages,
plus two flags rec8 and recr, where the subscripts refer to the sender and
receiver sides, to indicate that we are in a recovery phase, and a status component
giving the status of the last message sent. The status can be either
"?" denoting that the last message sent is still in queue, true denoting
that the last message sent has been successfully delivered to the user, or false. A status value of false, and
therefore a negative acknowledgement, only allows the user to conclude that there has been a crash, but
even in this situation the last message sent may have
been successfully delivered.3
|
send msg(m)
Eff: queue
:=queue "m status :=?
ack(b)
Pre: status = b
(E Bool) Eff: none
|
receive msg (m)
Pre: queue=() ~A hd queue = m Eff: queue := tl queue
if queue =
()
A status
=? then status :=true
|
crashV crashr
Eff: rec :=true Eff:
recr
:=true
lose
Pre:
rec =true V rec =true
Eff: delete arbitrary
elements of queue
if the element at the end of queue was deleted then status :=false
else
optionally
status :=false
 3Throughout this paper we
use the following operations on lists: let l be a list (e0,
... , eQ) with elements e0 through
eQ. Then l"m and tll denote the lists (e0,... ,eQ,m) and (ei,.. .,eQ), respectively,
and hdl and last l
denote the
elements e0 and eQ,
respectively.
3Throughout this paper we
use the following operations on lists: let l be a list (e0,
... , eQ) with elements e0 through
eQ. Then l"m and tll denote the lists (e0,... ,eQ,m) and (ei,.. .,eQ), respectively,
and hdl and last l
denote the
elements e0 and eQ,
respectively.


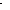
![Text Box: ] receive pktr (p) send pkt .V(p)
]
Channel rs](50-CorrectnessAMOMessagesOCR_files/image007.gif)





![Text Box: ]](50-CorrectnessAMOMessagesOCR_files/image013.gif)









![Text Box: ]](50-CorrectnessAMOMessagesOCR_files/image023.gif)



![Text Box: ]](50-CorrectnessAMOMessagesOCR_files/image027.gif) Figure 4. The Clock-Based Protocol C.
Figure 4. The Clock-Based Protocol C.
recover recoverr
Pre: rec
=true Pre:
recr =true
Eff: rec :=false Eff: recr
:=false
4.
CLOCK-BASED PROTOCOL C
Figure 4 shows the structure of the clock-based
protocol of [10], which we call C. An additional
component, "the clock subsystem", is needed to keep the local clocks
of the sender and the receiver "almost" synchronized.
Informally, the clock-based protocol works as
follows. The sender associates a time-stamp with each message it wishes to
transmit. The timestamps are obtained from the sender's
local clock time8. The receiver uses the associated timestamp to decide
whether or not to accept a received message—roughly, it
will accept a message provided that the
associated timestamp is greater than the timestamp of the last message that was
accepted. However, the receiver does not always remember the timestamp of the
last accepted message: it might forget this information because of a crash, or
simply because a long time has elapsed since the last message was accepted and
it is no longer efficient to remember it.
Therefore, the receiver uses safe time estimates determined from its own local clock (timer) to decide when to accept a message. The estimates are
kept in the variables lowerr and upperr;
the receiver accepts if the message's timestamp is in the interval (lowerr, upperr].
The lowerr bound is designed to be at least as big as the time of
the last message accepted. It can be bigger, however, as long as it is
sufficiently less than the receiver's local time (at least approximately a
one-way message delay less). This is because the receiver should not
accidentally fail to accept a valid message that takes the maximum time to
arrive. We note that the reason that we do not want to remember just the last
timestamp is that we envision using this protocol in parallel for many users,
and a single lowerr bound could be used for all users that have not sent
messages for a long while.
The upperr bound is chosen to be big enough so that the receiver
still accepts the most recent messages, even if they
arrive very fast. That is, it should be somewhat larger than the current time. But this bound will be kept in stable
storage, and therefore should not be updated
very often. Thus, it will generally be set to be a good deal larger than the
current local time. In particular, it will be
larger than the timestamp of any message so far accepted.
All that needs to be kept in stable storage is just the local clocks,
plus the one variable upperr of the receiver. When the receiver side crashes and recovers again, it
resets its lowerr bound to the old upperr bound, to be sure that it will not accept, and
thus deliver, any message twice. This explains why we
cannot just set upperr
to infinity.
There is also a simple acknowledgement protocol, which we do not
discuss in detail here.
We now consider how to model this protocol formally.
Since we are in a timed setting, the architecture
of the protocol consists of the parallel composition of a timed automaton for each of the sender and receiver, plus timed automata to
represent the two communication channels, plus an additional timed automaton to
represent an almost-synchronized clock subsystem.
Each
communication channel acts as follows. A send pkt(p) action places the indicated packet4 p in the channel. The channel
is allowed to lose, duplicate, and reorder any packets, but we will assume that for every k send pkt(p) actions for a
particular packet, at least
one packet p is not lost. For each such packet p, a receive pkt (p) action will occur within time d, the
maximum channel delay time. We note that it is possible to give a more abstract description of the channels; our
results do not depend on this particular description.
The clock
subsystem updates the local clocks of the sender and receiver by issuing tick actions in arbitrary ways so as to keep those clocks within e of real time. We do not describe the channels and
the clock subsystem formally in this paper.
For the sender and receiver, we first mention the
state variables not described above and then define the transition
relations.
For the
sender, mode8, ranging over idle, send, and rec, indicates whether the sender is idle, sending the current message to the
channel, or in recovery phase, respectively. The variable current-msg8 holds the current message, while last8 holds its timestamp. The list of messages buf8 contains the remaining messages waiting to be
sent. Finally, current-ack8 of type Bool holds the acknowledgement received from the
receiver.
For the receiver, moder, ranges over idle, rcvd, ack, and rec. rcvd indicates that packets have been received on the channel but the
associated messages not yet passed to the user, ack indicates that all messages have been passed to the user
and that the receiver is issuing positive acknowledgements, and finally rec indicates
the recovery phase. The list of messages bufr holds the messages received
from the channel but not yet passed to the user.
For the simple acknowledgement protocol, we have lastr to hold the timestamp of the last accepted message, and nack-bufr to hold
the timestamps for which negative acknowledgements
must be issued. Finally, the variable rm-timer is used by the cleanupr action.
The
definition of the steps is listed in the left column below for the sender and
in the right for the receiver. We
have aligned the send pkt and
corresponding receive
pkt actions to
 4llere and elsewhere, we use the term
"packet" to denote objects sent over the channels in an implementation;
we reserve the term "message" for the "higher-level",
user-meaningful messages that appear, e.g., in the specification.
4llere and elsewhere, we use the term
"packet" to denote objects sent over the channels in an implementation;
we reserve the term "message" for the "higher-level",
user-meaningful messages that appear, e.g., in the specification.
increase readability.
We treat timing requirements implicitly by giving
upper time bounds on certain classes of
actions. This corresponds to the way timing requirements are specified in [15].
The code contains three unspecified timing constants ci, /3, and p, to be
explained after the code.
send
msg(in)
Eff: if modes rec ~then buf s := buf s "in
choose
id(t)
Pre: modes =idle A buf s =() ~A times = t A t> lasts Eff: modes :=send
lasts := t
current-msg s := hd buf s
 buf s
:= ti buf s
buf s
:= ti buf s
|
send pktV.
(in, t)
Pre:
modes =send A
current-msg
s = in A lasts = t Eff: none
|
receive
pktsr (in, t)
Eff: if moder=rec ~then
if lowerr <t < upperr then
moder := rcvd
bufr := bufr
" in
lastr, lowerr :=t
else if lastr <t < lowerr then
nack-bufr :=
nack- buf r "t
else if moder =idle A
lastr = t then moder := ack
|
receive
msg (in)
Pre: moder = rcvd A bufr=() ~A hd bufr = in Eff: bufr := ti bufr
if bufr = () then
moder := ack
rm-timer :=timer
receive pktr s(t,
b)
Eff: if
modes =send A lasts = t then modes :=idle
current-acks := b
current-msg
s := nil
ack(b)
Pre: modes =idle A
buf s
= () A current-acks = b Eff: none
send pkt UV(t, true)
Pre: moder = ack A lastr = t Eff: moder :=idle
send pkt UV(t, false)
Pre: moder=rec ~A
nack-bufr=() ~A hd nack-buf
r =t Eff: nack-bufr := ti nack-bufr
recovers recoverr
Pre: modes = rec Pre: moder = rec A upperr + 2€ < timer
Eff: modes :=idle Eff: moder :=idle
lasts :=times lastr := 0
rm-timer :=
00 rm-timer :=00
buf s := () bufr, nack-bufr := ()
current-msg
s := nil lowerr := upperr
current-acks
:=false upperr :=timer + /3
increase-lowerr (t)
Pre: moder=rec ~A lowerr <t < timer - 13
Eff: lowerr :=t
increase-upperr (t)
Pre: moder=rec ~A upperr <t =timer + /3
Eff: upperr := t
cleanupr
Pre:
moder E {idle, ack} A
timer > rm-timer + m
Eff: moder :=idle
lastr :=0
rm-timer :=00
ticks(t) tickr (t)
Eff: times :=
t Eff: timer :=t
The correctness of the clock-based protocol requires that
we put upper time bounds on one set of actions of the sender.
Informally,
· every time a send pkt8 U(m, t) action becomes possible (or stays possible after being
executed), it must occur within time l8 unless it gets disabled in
the meantime.
Similarly, for the receiver we need to put upper
bound on two classes of actions:
·
send pktU8(id, true) has an
upper bound of lU, and
·
increase-upperr (t) has an upper bound of l~ U.
The correctness of the protocol depends on the
timing constants in the code being related
properly to these time bounds, and to channel and local clock characteristics.
The requirements are: 3> 2e+l~ U, p> kl8+d+2e, and ci > k(lU +d)+(k-1)kl8+2e. Note, how all three constants depend on the maximum difference
of 2e between
the local clocks.
In this paper we do not give a formal
specification of H. Unlike C, which uses timing assumptions,
H uses
handshakes to first make the sender and receiver agree on a message identifier and then perform the actual message
transmission. An additional packet type is used as cleanup information.
We proceed by describing the generic protocol C.
5. GENERIC PROTOCOL C
The two protocols C and H both go through three major
phases during normal operation:
Choosing a message identifier The sender picks an identifier id that is within the set of
identifiers that the receiver is willing to accept. In C time bounds are used to choose a good identifier; in H an initial handshake between the sender and the receiver is used.
Sending the message and getting acknowledgement This phase is similar in
both C and H. The sender (re)transmits the
current message with the chosen id,
until it receives an acknowledgement packet for
that id.
Cleaning up
Here again, C uses time bounds (in particular timeouts) whereas H uses
a
handshake to determine when some "old" information may be discarded.
Our generic protocol C is designed to capture these three phases in an abstract way that both C and H implement. The key abstractions incorporated into
the protocol C are two
variables, good8 and goody. The variable good8 represents the identifiers that the sender might shortly assign to messages, and goody represents the identifiers
that the receiver is willing to accept.
Four
actions of C deal with "growing" and
"shrinking" good8 and goody, respectively. As an example, remember that in C the identifier for the current message is taken from
the sender's local clock time8. Every time the local clock time8 is advanced, the identifier that the sender might assign to the current
message is changed from the old value of time8 to the new value. In C this corresponds to first
"shrinking" good8 with the old value and then "growing" it
with the new value.
The preconditions of the grow and shrink actions are designed to
preserve certain key invariants,
one of which we will present in Section 6. We actually allow more freedom in these actions than is actually needed by C and H. This leaves open the possibility that other low-level protocols, other than C
and H,
can be proved to be implementations of C. We show the parts of C that deal with good8 and goody.
send msg(m) ~ ~ ~
prepare
Pre: modes =idle A buf s =()~ Eff: modes := needid
goods := I J
current-msg s := hd buf s
buf s := ti buf s
if moder=rec ~then current-ok :=true
choose id(id)
Pre: modes = needid A id E goods Eff: modes :=send
lasts := id
useds :=
usedsAid
 receive pktsy(m, id)
receive pktsy(m, id)
Eff: if
modey=rec ~then
if id E goody then
modey := rcvd
bufy := bufy Am
lasty :=id
goody :=goody \ {id'
M id'
< id}
if id =lasts A modes =send then current-ok :=false
else if
id=lasty ~then
optionally
nack-bufy := nack- buf y Aid else if modey =idle then
modey := ack
receive msg(m) ~ ~ ~
receive
pkty s(id, b) ~~~ send
pktU, (id, true) ~ ~ ~
ack(b) ~~~ send
pktUV(id,false) ~ ~ ~
crashs~~~ crashy ~ ~ ~
recovers ~~~ recovery ~ ~ ~
shrink goods(ids)
Pre: none
Eff: goods :=goods \ ids
grow goods(ids)
Pre: modes=needid ~V
((modey=rec ~== ids c issuedy) A
(current-ok =true == ids c goody) A (ids fl
useds = {
}))
Eff:
goods :=goods U ids
shrink goody(ids)
Pre: current-ok =false V
((modes = needid == ids fl goods = {
}) A (modes =send == lasts E ids))
Eff:
goody :=goody \ ids
grow
goody(ids)
Pre:
ids fl issuedy = { }
Eff: goody :=goody U ids issuedy :=
issuedy U ids
cleanupy
Pre: modey E
{idle, ack} A
(modes =send == lasts=lasty)~ Eff:
modey :=idle
lasty := nil
6.
CORRECTNESS PROOFS
In this section we sketch the
proofs of safe implementation for the different levels of abstraction in our work. We will not be strictly formal.
For such formal treatment and full proofs we refer to our full report
[8].
6.1. Correctness of C
To prove
that C is a safe implementation of S, we need a backward simulation. Informally this is because C (and the lower-level protocols) may postpone the
decisions about which messages to lose because of a crash till after recovery,
whereas in S message loss occurs between crash and recovery. It is due to certain race conditions on the channels that the
decisions are delayed in C, C, and H.
Since a backward simulation directly from C
to S is still more complicated than
we would like, we split the task one more
time. Our strategy is to try to localize the backward simulation reasoning, because reasoning in
this way seems to be inherently difficult compared to the more intuitive forward simulation and refinement
mapping techniques. Thus, we define a
new, "delayed-decision" version D of the specification (see
Figure 1). D is just like S except that it delays the point at which the
decision about loss of messages is made.
Now, when a crash occurs, messages in the system and status may get marked. Later, even after
recovery, any marked message is allowed to be lost. Also, a marked status
is allowed to be lost, i.e., changed to false.
Due to
space constraints we will not define D formally,
nor will we define or prove the backward simulation from D to S. We only note that such a backward simulation exists, which allows us to conclude that D
safely implements S.
The proof
that C safely implements D uses
certain invariants. For instance, the following key invariant of C states that when no crashes
have occurred since the sender executed
a prepare action (i.e., current-ok =true) and the sender still has not chosen an identifier, then the sender can only choose
identifiers that are considered good by the receiver. The shrink good and grow good actions
are explicitly designed to preserve this invariant
(among others).
If current-ok
=true A mode8 = needid then good8
t goody.
The proof that C safely implements D is now discharged by
exhibiting a refinement mapping
from C to D. Again, we
do not give details, but refer to [8] for the complete proofs.
Together,
the existence of the backward simulation from D to S and the refinement mapping from C to D allow us to conclude that C safely implements S.
6.2. Correctness of C and H
To prove
that C and H safely
implement S we just have to prove some simulations from C and H to C, since we have already shown that C safely implements S. We only consider C.
The first
step, a technical one, in the correctness proof involves adding a history
variable [16] deadline to C to get an equivalent
version of the protocol (which we still call C). The
variable deadline is set to the current real time plus a maximum
one-way delay when the
current message gets a timestamp, and gets reset (to oo) when either a crash
occurs or the current message gets
accepted by the receiver. Below we show an invariant that states that this deadline is always met in any
execution of C. Another history variable used8
is a list containing the timestamps used so far.
Next, note
that C is formalized as an untimed automaton whereas C is formalized as a timed
automaton. We resolve this model inconsistency by converting C into the
timed
model to get GW. That is, an untimed automaton
can be considered to be a timed automaton,
where time can pass arbitrarily. (Additional liveness restrictions on G will make sure that time-passage is not the only activity of GW). Below we prove that C safely implements G in the
timed setting. Certain embedding results
then allow us to conclude that
since G safely implements S, Gt safely implements the converted specification SW, which furthermore implies that C
safely implements SW. Thus, the
embedding results allow us to work mostly within the simpler untimed model.
Definition 1 (Refinement from
C to GW) If s is a state of C then R&0 (s) is the state u of G such that
 u.good8 = {s.time8} - {s.last8}
u.good8 = {s.time8} - {s.last8}
u.good y = (s.lowery, s.uppery]
u.issuedy = (0, s.uppery]
u.current-ok = (s.deadline=oo)~
All remaining variables (including the channels)
have the same contents in C and GW.
The timestamp that the sender
in C might associate with a message, corresponding to good8 in G, is
taken from the local clock time8, but only if the local clock has advanced since the last timestamp (last8). This explains the line for good8. The lines for goody and issuedy can be
explained similarly.
A key
invariant we need in the refinement proof is that the history variable deadline of C is always at least as big as
real time, i.e., now deadline. This can
then be used to prove the
following invariant: for all timestamps t on the
channel from sender to receiver, deadline=oo ~== uppery > t. This invariant states that uppery
is always sufficiently large when the current message is being transmitted on the channel and
no crashes have occurred.
Lemma 2 R&0 is a refinement mapping from C to GW.
Proof The proof of a refinement mapping in the timed
setting has three points, which we sketch here:
·
For any state s of C, Rcc(s) has the same real time (now) as s. This is satisfied immediately by the definition of R&0.
· For any
start state s of C,
Rcc(s) is a start state of GW.
This is easy to check.
·
For each
step (s, a, s') of C, where s and s'
satisfy the invariants of C, we must show the existence of a sequence of steps (Rcc(s), a1, ... , aQ, Rcc(s')) of G with the same trace (see Figure 2). We conduct such a proof by doing a case analysis based on the different actions a of C. For instance, if a = increase-lowery(t), we show that (Rcc(s), shrink goody((0, t]), Rcc(s')) is a step of GW.
 The correctness of H can also
be proved using the refinement mapping technique.
The correctness of H can also
be proved using the refinement mapping technique.
7.
CONCLUSION
In this paper, we have used a
simple automaton model to present the at-most-once message delivery problem and two interesting solutions, and
have used simulation techniques to prove
that the two algorithms meet the specification. We have only given arguments for safety and timing properties here, and have left
liveness for a longer report. We believe
that this work yields important insights into the protocols, and also serves to
show the adequacy of the model and proof techniques.
Similar protocols have been verified formally, using different
techniques. LOTOS has, for instance, been used in [14].
There is a considerable amount of further work
remaining. First, if the timing assumptions on C are weakened or removed, the
resulting algorithm still will not deliver any message more than once; however,
it may lose messages even in the absence of a crash. It remains to formulate the weaker specification and
prove that the weaker version of C satisfies it.
Second, there are other algorithms that solve the
at-most-once message delivery problem, for
example, using bounded identifier spaces or cryptographic assumptions. We would like also to verify these, again reusing as much of
our proofs as possible. In [17] bounded identifier spaces are
dealt with for similar protocols.
Third, we would like to automate our simulation
proofs using a mechanical theorem prover.
We have already begun this work, by proving the equivalence of versions of S and D using the Larch Prover [18,
4]. We have been pleased with the preliminary results: the prover has not only been able to check our hand proofs,
but in fact has been able to fill in many of the details. We can
draw several conclusions:
· Automata, invariants, and simulations are all excellent
tools for verifying timed and untimed communication protocols. The methods
scale well, yield insight, and are not too difficult to use.
· A general model such as timed automata is needed in order
to model and verify most communication protocols in a
single coherent framework. However, for reasoning about particular protocols, it is often better to work
in a simplified special case of the
general model. (For instance, for untimed protocols such as H, it is best to avoid details of timing.) What is needed is a collection
of special models, each of which can be easily "embedded" in
the general model.
· Safety proofs are challenging. They require insight to
obtain the right invariants and simulations,
and a lot of detailed work to verify these choices. Computer assistance can
help with the details; however, the insight will always be required.
· Backward simulations are much harder to do than
refinements and forward simulations but are necessary in certain
situations.
· Many algorithms can be treated as implementations of a
common abstract algorithm.
· Verifying a coordinated collection of protocols, rather
than just a single isolated protocol, is extremely
valuable. It leads to the discovery of useful abstractions, and tends
to make the proofs more elegant and reusable.
• Doing proofs for realistic communication
protocols is feasible now. We predict that it will become more so, and
will be of considerable practical importance.
REFERENCES
1. M.
Abadi and L. Lamport. The existence of refinement mappings. Theoretical
Compnter Science, 82(2):253^284, May 1991.
2. M. Abadi and L. Lamport. An old-fashioned recipe for real
time. In J. W. de Dakker, C. Huizing, and G.
Rozenberg, editors, Proceedings of REX Workshop "Real-Time: Theory in Practice", Mook, The Netherlands, Jnne 1991,
number 600 in Lecture Notes in Computer Science, pages 1-27.
Springer-Verlag, 1992.
3. D. Belsnes. Single message communication. IEEE
Transactions on Commnnications, Com24(2), February 1976.
4. Stephen J. Garland and John V. Guttag. A guide to LP, the
Larch Prover. Technical Report 82, DEC, Systems Research Center, December
1991.
5. R. Gawlick, N. Lynch, R. Segala, and J. Søgaard-Andersen.
Liveness in timed and untimed systems. Technical report, MIT, Laboratory
for Computer Science, 1993.
6. B. Jonsson. Simulations between specifications of
distributed systems. In J. C. M. Baeten and J. F. Groote, editors,
Proceedings of CONCUR '91.2nd International Conference on Concnrrency Theory,
Amsterdam, The Netherlands, Angnst 1991, number 527 in Lecture Notes in
Computer Science, pages 346^360. Springer-Verlag, 1991.
7. S. S.
Lam and A. U. Shankar. Protocol verification via projections. IEEE Transactions
on Software Engeneering, 10(4), 1984.
8. B. Lampson, N. Lynch, and J. Søgaard-Andersen. Reliable
at-most-once message delivery protocols. Technical report, MIT,
Laboratory for Computer Science, 1993. Full report.
9. B. Liskov. Practical uses of synchronized clocks in
distributed systems. In Proceedings of the Tenth
Annnal ACM Symposinm on Principles of Distribnted Compnting, pages 1-10, 1991.
10. B. Liskov, L. Shrira, and J. Wroclawski. Efficient
at-most-once messages based on synchronized clocks. ACM Transactions
on Compnter Systems, 9(2):125^142, May 1991.
11. N.
Lynch and M. Tuttle. Hierarchical correctness proofs for distributed
algorithms. Technical Report MIT/LCS/TR-387, MIT, Laboratory for Computer
Science, Cambridge, MA, 02139, April 1987.
12. N. Lynch and M. Tuttle. An introduction to Input/Output
automata. CWI-Qnarterly, 2(3):219-246, September 1989.
13.
N. Lynch and F. Vaandrager. Forward and backward
simulations for timing-based systems. In J.
W. de Dakker, C. Huizing, and G. Rozenberg, editors, Proceedings of REX Workshop "Real-Time: Theory in Practice",
Mook, The Netherlands, Jnne 1991, number 600 in Lecture Notes in
Computer Science, pages 397-446. Springer-Verlag, 1992.
14. Eric Madelaine and Didier Vergamini. Specification and
verification of a sliding window protocol
in LOTOS. In K. R. Parker and G. A. Rose, editors, Formal Description
Techniqnes, IV, pages 495-510. North-Holland, 1991.
15. M.
Merritt, F. Modugno, and M. Tuttle. Time-constrained automata. In Proceedings
of CONCUR '91. 2nd International Conference on
Concnrrency Theory, Amsterdam, The
Netherlands, Angnst 1991, number 527 in Lecture Notes in Computer
Science, pages 408-
423.
Springer-Verlag, 1991.
16. S.
Owicki and D. Gries. An axiomatic proof technique for parallel programs I. Acta
Informatica, 6(4):319-340, 1976.
17. A. U. Shankar. Verified data transfer protocols with
variable flow control. ACM Transactions on Compnter Systems,
7(3):281-316, August 1989.
18.
Jørgen F. Søgaard-Andersen,
Stephen J. Garland, John V. Guttag, Nancy A. Lynch, and Anna
Pogosyants. Computer-assisted simulation proofs. In Costas Courcoubetis,
editor, Compnter Aided Verification. 5th International Conference, CAV '93.
Elonnda, Greece, Jnne/Jnly 1993, volume 697
of Lectnre Notes in Compnter Science, pages 305-319. SpringerVerlag,
1993.
![]() eResearch supported in
part by the Danish Research Academy.
eResearch supported in
part by the Danish Research Academy.



