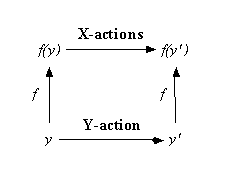
Chapter 10
Reliable Messages and Connection Establishment
Butler W. Lampson
Note: This web page was converted automatically from a Word original. There may be problems with the formatting and the pictures. To see the intended form, follow one of the links below.
Citation: B. Lampson. Reliable messages and connection establishment. In Distributed Systems, ed. S. Mullender, 2nd ed., Addison-Wesley, 1993, pp 251-281. This chapter is the result of joint work with Nancy Lynch and Jørgen Søgaard-Andersen.
Links: Abstract, Postscript, Acrobat, Word.
Email: blampson@microsoft.com. This paper is at http://www.research.microsoft.com.
10.1 Introduction
Given an unreliable network, we would like to reliably deliver messages from a sender to a receiver. This is the function of the transport layer of the ISO seven-layer cake. It uses the network layer, which provides unreliable message delivery, as a channel for communication between the sender and the receiver.
Ideally we would like to ensure that
• messages are delivered in the order they are sent,
• every message sent is delivered exactly once, and
• an acknowledgement is returned for each delivered message.
Unfortunately, it’s expensive to achieve the second and third goals in spite of crashes and an unreliable network. In particular, it’s not possible to achieve them without making some change to stable state (state that survives a crash) every time a message is received. Why? When we receive a message after a crash, we have to be able to tell whether it has already been delivered. But if delivering the message doesn’t change any state that survives the crash, then we can’t tell.
So if we want a cheap deliver operation which doesn’t require writing stable state, we have to choose between delivering some messages more than once and losing some messages entirely when the receiver crashes. If the effect of a message is idempotent, of course, then duplications are harmless and we will choose the first alternative. But this is rare, and the latter choice is usually the lesser of two evils. It is called ‘at-most-once’ message delivery. Usually the sender also wants an acknowledgement that the message has been delivered, or in case the receiver crashes, an indication that it might have been lost. At-most-once messages with acknowledgements are called ‘reliable’ messages.
There are various ways to implement reliable messages. An implementation is called a ‘protocol’, and we will look at several of them. All are based on the idea of tagging a message with an identifier and transmitting it repeatedly to overcome the unreliability of the channel. The receiver keeps a stock of good identifiers that it has never accepted before; when it sees a message tagged with a good identifier, it accepts it, delivers it, and removes that identifier from the good set. Otherwise, the receiver just discards the message, perhaps after acknowledging it. In order for the sender to be sure that its message will be delivered rather than discarded, it must tag the message with a good identifier.
What makes the implementations tricky is that we expect to lose some state when there is a crash. In particular, the receiver will be keeping track of at least some of its good identifiers in volatile variables, so these identifiers will become bad at the crash. But the sender doesn’t know about the crash, so it will go on using the bad identifiers and thus send messages that the receiver will reject. Different protocols use different methods to keep the sender and the receiver more or less in sync about what identifiers to use.
In practice reliable messages are most often implemented in the form of ‘connections’. The idea is that a connection is ‘established’, any amount of information is sent on the connection, and then the connection is ‘closed’. You can think of this as the sending of a single large message, or as sending the first message using one of the protocols we discuss, and then sending later messages with increasing sequence numbers. Usually connections are full-duplex, so that either end can send independently, and it is often cheaper to establish both directions at the same time. We ignore all these complications in order to concentrate on the essential logic of the protocols.
What we mean by a crash is not simply a failure and restart of a node. In practice, protocols for reliable messages have limits, called ‘timeouts’, on the length of time for which they will wait to deliver a message or get an ack. We model the expiration of a timeout as a crash: the protocol abandons its normal operation and reports failure, even though in general it’s possible that the message in fact has been or will be delivered.
We begin by writing a careful specification S for reliable messages. Then we present a ‘lower-level’ spec D in which the non-determinism ;associated with losing messages when there is a crash is moved to a place that is more convenient for implementations. We explain why D implements S but don’t give a proof, since that requires techniques beyond the scope of this chapter. With this groundwork, we present a generic protocol G and a proof that it implements D. Then we describe two protocols that are used in practice, the handshake protocol H and the clock-based protocol C, and show how both implement G. Finally, we explain how to modify our protocols to work with finite sets of message identifiers, and summarize our results.
The goals of this chapter are to:
• Give a simple, clear, and precise specification of reliable message delivery in the presence of crashes.
• Explain the standard handshake protocol for reliable messages that is used in TCP, ISO TP4, and many other widespread communication systems, as well as a newer clock-based protocol.
• Show that both protocols can be best understood as special cases of a simpler, more general protocol for using identifiers to tag messages and acknowledgements for reliable delivery.
• Use the method of abstraction functions and invariants to help in understanding these three subtle concurrent and fault-tolerant algorithms, and in the process present all the hard parts of correctness proofs for all of them.
• Take advantage of the generic protocol to simplify the analysis and the arguments.
10.1.1 Methods
We use the definition of ‘implements’ and the abstraction function proof method explained in Chapter 3. Here is a brief summary of this material.
Suppose that X and Y are state machines with named transitions called actions; think of X as a specification and Y as an implementation. We partition the actions of X and Y into external and internal actions. A behavior of a machine M is a sequence of actions that M can take starting in an initial state, and an external behavior of M is the subsequence of a behavior that contains only the external actions. We say Y implements X iff every external behavior of Y is an external behavior of X. This expresses the idea that what it means for Y to implement X is that from the outside you don’t see Y doing anything that X couldn’t do.
The set of all external behaviors is a rather complicated object and difficult to reason about. Fortunately, there is a general method for proving that Y implements X without reasoning explicitly about behaviors in each case. It works as follows. First, define an abstraction function f from the state of Y to the state of X. Then show that Y simulates X:
1. f maps an initial state of Y to an initial state of X.
2. For each Y-action and each reachable state y there is a sequence of X-actions (perhaps empty) that is the same externally, such that the following diagram commutes.
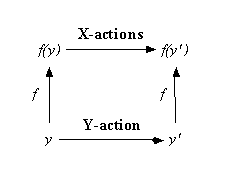
A sequence of X-actions is the same externally as a Y-action if they are the same after all internal actions are discarded. So if the Y-action is internal, all the X-actions must be internal (perhaps none at all). If the Y-action is external, all the X-actions must be internal except one, which must be the same as the Y-action.
A straightforward induction shows that Y implements X: For any Y-behavior we can construct an X-behavior that is the same externally, by using (2) to map each Y-action into a sequence of X-actions that is the same externally. Then the sequence of X-actions will be the same externally as the original sequence of Y-actions.
In order to prove that Y simulates X we usually need to know what the reachable states of Y are, because it won’t be true that every action of Y from an arbitrary state of Y simulates a sequence of X-actions; in fact, the abstraction function might not even be defined on an arbitrary state of Y. The most convenient way to characterize the reachable states of Y is by an invariant, a predicate that is true of every reachable state. Often it’s helpful to write the invariant as a conjunction, and to call each conjunct an invariant. It’s common to need a stronger invariant than the simulation requires; the extra strength is a stronger induction hypothesis that makes it possible to establish what the simulation does require.
So the structure of a proof goes like this:
• Establish invariants to characterize the reachable states, by showing that each action maintains the invariants.
• Define an abstraction function.
• Establish the simulation, by showing that each Y-action simulates a sequence of X-actions that is the same externally.
This method works only with actions and does not require any reasoning about behaviors. Furthermore, it deals with each action independently. Only the invariants connect the actions. So if we change (or add) an action of Y, we only need to verify that the new action maintains the invariants and simulates a sequence of X-actions that is the same externally. We exploit this remarkable fact in Section 10.9 to extend our protocols so that they use finite, rather than infinite, sets of identifiers.
In what follows we give abstraction functions and invariants for each protocol. The actual proofs that the invariants hold and that each Y-action simulates a suitable sequence of X-actions are routine, so we give proofs only for a few sample actions.
10.1.2 Types and NNotation
We use a type M for the messages being delivered. We assume nothing about M.
All the protocols except S and D use a type I of identifier;s for messages. In general we assume only that Is can be compared for equality; C assumes a total ordering. If x is a multiset whose elements have a first I component, we write ids(x) ;for the multiset of Is that appear first in the elements of x.
We write
á...ñ for a sequence with the indicated elements and + for concatenation of sequences. We view a sequence as a multiset in the obvious way. We write x = (y, *) to mean that x is a pair whose first component is y and whose second component can be anything, and similarly for x = (*, y).We define an action by giving its name, a guard that must be true for the action to occur, and an effect described by a set of assignments to state variables. We encode parameters by defining a whole family of actions with related names; for instance, get(m) is a different action for each possible m. Actions are atomic; each action completes before the next one is started.
To express concurrency we introduce more actions. Some of these actions may be internal, that is, they may not involve any interaction with the client of the protocol. Internal actions usually make the state machine non-deterministic, since they can happen whenever their guards are satisfied, not just when there is an interaction with the environment. We mark external actions with *s, two for an input action and one for an output action. Actions without *s are internal.
It’s convenient to present the sender actions on the left and the receiver actions on the right. Some actions are not so easy to categorize, and we usually put them on the left.
10.2 The Specification S
The specification S for reliable messages is a slight extension of the spec for a fifo queue. Figure 10.1 shows the external actions and some examples of its transitions. The basic state of S is the fifo queue q of messages, with put(m) and get(m) actions. In addition, the status variable records whether the most recently sent message has been delivered. The sender can use getAck(a) to get this information; after that it may be forgotten by setting status to lost, so that the sender doesn’t have to remember it forever. Both sender and receiver can crash and recover. In the absence of crashes, every message put is delivered by get in the same order and is positively acknowledged. If there is a crash, any message still in the queue may be lost at any time between the crash and the recovery, and its ack may be lost as well.
The getAck(a) action reports on the message most recently put, as follows. If there has been no crash since it was put there are two possibilities:
• the message is still in q and getAck cannot occur;
• the message was delivered by get(m) and getAck(OK) occurs.
If there have been crashes, there are two additional possibilities:
• the message was lost and getAck(lost) occurs;
• the message was delivered or is still in q but getAck(lost) occurs anyway.
The ack makes the most sense when the sender alternates put(m) and getAck(a) actions. Note that what is being acknowledged is delivery of the message to the client, not its receipt by some part of the implementation, so this is an end-to-end ;ack. In other words, the get should be thought of as including client processing of the message, and the ack might include some result returned by the client such as the result of a remote procedure call. This could be expressed precisely by adding an ack action for the client. We won’t do that because it would clutter up the presentation without improving our understanding of how reliable messages work.
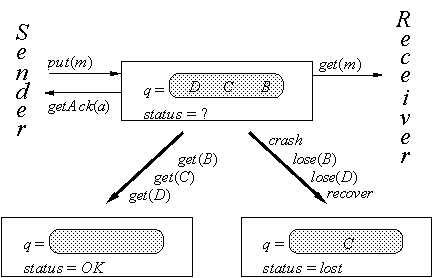
To define S we introduce the types A (for acknowledgement) with values in {OK, lost} and Status with values in {OK, lost, ?}. Table 10.1 gives the state and actions of S. Note that it says nothing about channels; they are part of the implementation and have nothing to do with the spec.
Why do we have both crash and recover actions, as opposed to just a crash action? A spec which only allows messages to be lost at the time of a crash is not implemented by a protocol like C in which the sender accepts a message with put and sends it without verifying that the receiver is running normally. In this case the message is lost even though it wasn’t in the system at the time of the crash. This is why we have a separate recover
r action which allows the receiver to declare the point after a crash when messages are again guaranteed not to be lost. There seems to be no need for a recovers action, but we have one for symmetry.A spec which only allows messages to be lost at the time of a recover is not implemented by any protocol that can have two messages in the network at the same time, because after a crash
s and before the following recovers it’s possible for the second message in the network to be delivered, which means that the first one must be lost to preserve the fifo property.|
|
Sender |
|
|
Receiver |
|
|||
|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|||
|
**put(m) |
rec s = false |
append m to q, |
*get(m) |
rec r = false,m is first on q |
remove head of q, |
|||
|
*getAck(a) |
rec s = false, status = a |
optionally |
|
|
|
|||
|
**crash s |
|
rec s := true |
**crash r |
|
rec r := true |
|||
|
*recover s |
rec s |
rec s := false |
*recover r |
rec r |
rec r := false |
|||
|
lose |
rec s or recr |
delete some element from q; |
|
|
|
|||
The simplest spec which covers both these cases can lose a message at any time between a crash and its following recover, and we have adopted this alternative.
10.3 The Delayed-Decision Specification D
Next we introduce an implementation of S, called the delayed-decision specification ;D, that is more non-deterministic about when messages are lost. The reason for D is to simplify the proofs of the protocols: with more freedom in D, it’s easier to prove that a protocol simulates D than to prove that it simulates S. A typical protocol transmits messages from the sender to the receiver over some kind of channel which can lose messages; to compensate for these losses, the sender retransmits. If the sender crashes with a message in the channel it stops retransmitting, but whether the receiver gets the message depends on whether the channel loses it. This may not be decided until after the sender has recovered. So the protocol doesn’t decide whether the message is lost until after the sender has recovered. D has this freedom, but S does not.
D is the same as S except that the decisions about which messages to lose at recovery, and whether to lose the ack, are made by asynchronous drop actions that can occur after recovery. Each message in q, as well as the status variable, is augmented by an extra component ;of type Mark which is normally + but may become # between crash and recovery because of a mark action. At any time an unmark action can change a mark from # back to +, a message marked # can be lost by drop, or a status marked # can be set to lost by drop. Figure 10.2 gives an example of the transitions of D; the + marks are omitted.
|
|
Sender |
|
|
Receiver |
|
|||||||||||||
|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|||||||||||||
|
**put(m) |
recs = false |
append (m, +) to q, |
*get(m) |
recr = false,(m, *) first on q |
remove head of q, |
|||||||||||||
|
*getAck(a) |
recs = false, status = (a, *) |
status := (a, +)or status := (lost, +) |
|
|
|
|||||||||||||
|
**crashs |
|
recs := true |
**crashr |
|
recr := true |
|||||||||||||
|
*recovers |
recs |
recs := false |
*recoverr |
recr |
recr := false |
|||||||||||||
|
mark |
recs or recr |
for some element |
unmark |
|
for some element |
|||||||||||||
|
drop |
|
delete an element of q with mark = #; |
|
|
|
|||||||||||||
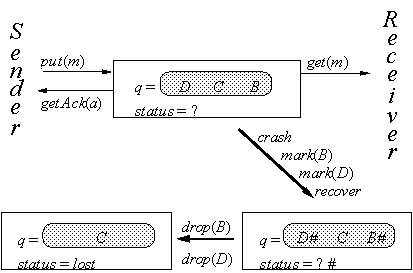
To define D we introduce the type Mark which has values in the set {+, #}. Table 10.2 gives the state and actions of D.
10.3.1 Proof that D Implements S
We do not give this proof, since to do it using abstraction functions we would have to introduce ‘prophecy variables’, also known as ‘multi-valued mappings’ or ‘backward simulations’ (Abadi and Lamport [1991], Lynch and Vaandrager [1993]). If you work out some examples, however, you will probably see why the two specs S and D have the same external behavior.
10.4 Channels
|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|
**sendsr(p) |
|
add some number of copies of p to sr |
**sendrs(p) |
|
add some number |
|
*rcvsr(p) |
p Î sr |
remove one p |
rcvrs (p) |
p Î rs |
remove one p |
|
losesr (p) |
p Î sr |
remove one p |
losers (p) |
p Î rs |
remove one p |
All our protocols use the same channel abstraction to transfer information between the sender and the receiver. We use the name ‘packet’ for the messages sent over a channel, to distinguish them from reliable messages. A channel can freely drop and reorder packets, and it can duplicate a packet any finite number of times when it’s sent; the only thing it isn’t allowed to do is deliver a packet that wasn’t sent. The reason for using such a weak specification is to ensure that the reliable message protocol will work over any bit-moving mechanism that happens to be available. With a stronger channel spec, for instance one that doesn’t reorder packets, it’s possible to have somewhat simpler or more efficient implementations.
There are two channels sr and rs, one from sender to receiver and one from receiver to sender, each a multiset of packets initially empty. The nature of a packet varies from one protocol to another. Table 10.3 gives the channel actions.
Protocols interact with the channels through the external actions send(...) and rcv(...) which have the same names in the channel and in the protocol. One of these actions occurs if both its pre-conditions are true, and the effect is both the effects. This always makes sense because the states are disjoint.
10.5 The Generic Protocol G
The generic protocol ;G generalizes two practical protocols described later, H and C; in other words, both of them implement G. This protocol can’t be implemented directly because it has some ‘magic’ actions that use state from both sender and receiver. But both real protocols implement these actions, each in its own way.
The basic idea is derived from the simplest possible distributed implementation of S, which we call the stable protocol ;SB. In SB all the state is stable (that is, nothing is lost when there is a crash), and each end keeps a set g
s or gr of good identifiers, that is, identifiers that have not yet been used. Initially gs Í gr, and the protocol maintains this as an invariant. To send a message the sender chooses a good identifier i from gs, attaches i to the message, moves i from gs to a lasts variable, and repeatedly sends the message. When the receiver gets a message with a good identifier it accepts the message, moves the identifier from gr to a lastr variable, and returns an ack packet for the identifier after the message has been delivered by get. When the receiver gets a message with an identifier that isn’t good, it returns a positive ack if the identifier equals lastr and the message has been delivered. The sender waits to receive an ack for lasts before doing getAck(OK). There are never any negative acks, since nothing is ever lost.This protocol satisfies the requirements of S; indeed, it does better since it never loses anything.
1. It provides at-most-once delivery because the sender never uses the same identifier for more than one message, and the receiver accepts an identifier and its message only once.
2. It provides fifo ordering because at most one message is in transit at a time.
3. It delivers all the messages because the sender’s good set is a subset of the receiver’s.
4. It acks every message because the sender keeps retransmitting until it gets the ack.
The SB protocol is widely used in practice, under names that resemble ‘queuing system’. It isn’t used to establish connections because the cost of a stable storage write for each message is too great.
In G we have the same structure of good sets and last variables. However, they are not stable in G because we have to update them for every message, and we don’t want to do a stable write for every message. Instead, there are operations to grow and shrink the good sets; these operations maintain the invariant g
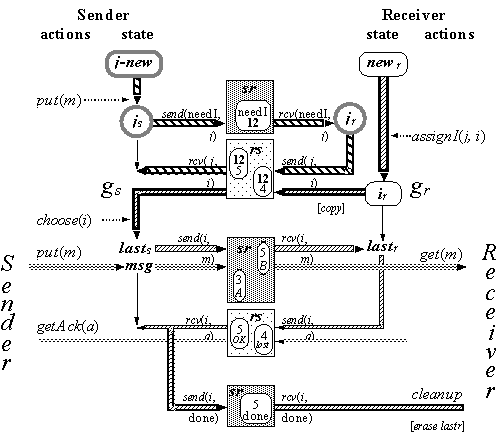
s Í gr as long as there is no receiver crash. When there is a crash, messages and acks can be lost, but S and D allow this. Figure 10.3 shows the state and some possible transitions of G in simplified form. The names in outline font are state variables of D, and the corresponding values are the values of the abstraction function in that state.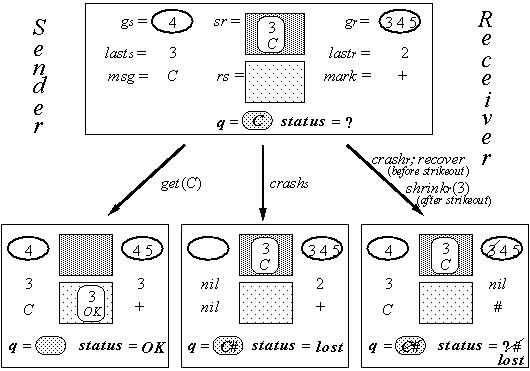
Figure 10.4 shows the state of G, the most important actions, and the S-shaped flow of information. The new variables in the figure are the complement of the used variables in the code. The heavy lines show the flow of a new identifier from the receiver to the sender, back to the receiver along with the message, and then back again to the sender along with the acknowledgement.
G also satisfies the requirements of S, but not quite in the same way as SB.
1. At-most-once delivery is the same as in SB.
2. The sender may send a message after a crash without checking that a previous outstanding message has actually been received. Thus more than one message can be in transit at a time, so there must be a total ordering on the identifiers in transit to maintain fifo ordering of the messages. In G this ordering is defined by the order in which the sender chooses identifiers.
3. Complete delivery is the same as in SB as long as there is no receiver crash. When the receiver crashes g
4. As in SB, the sender keeps retransmitting until it gets an ack, but since messages can be lost, there must be negative as well as positive acks. When the receiver sees a message with an identifier that is not in g
r and not equal to lastr it optionally returns a negative ack. There is no point in doing this for a message with i < lastr because the sender only cares about the ack for lasts, and the protocol maintains the invariant lastr £ lasts. If i > lastr, however, the receiver must sometimes send a negative ack in response so that the sender can find out that the message may have been lost.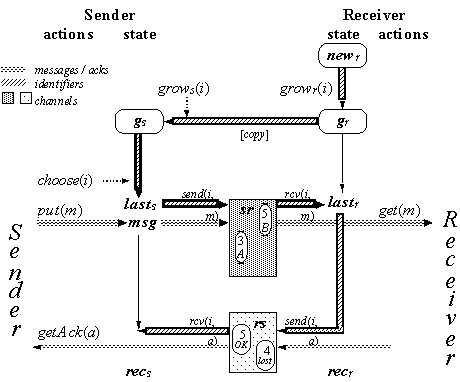
G is organized into a set of implementable actions that also appear, with very minor variations, in both H and C, plus the magic grow, shrink, and cleanup actions that are simulated quite differently in H and in C.
When there are no crashes, the sender and receiver each go through a cycle of modes, the sender perhaps one mode ahead. In one cycle one message is sent and acknowledged. For the sender, the modes are idle, [needI], send; for the receiver, they are idle and ack. An agent that is not idle is busy. The bracketed mode is ‘internal’: it’s possible to advance to the next mode without receiving another message. The modes are not explicit state variables, but instead are derived from the values of the msg and last variables, as follows:
mode
To define G we introduce the types:
I, an infinite set of identifiers.
P (packet), a pair (I, M or A).
The sender sends (I, M) packets to the receiver, which sends (I, A) packets back. The I is there to identify the packet for the destination. We define a partial order on I by the rule that i < i' iff i precedes i' in the sequence used
s.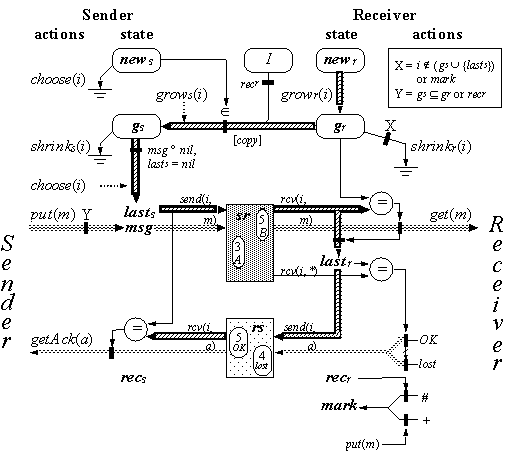
The G we give is a somewhat simplified version, because the actions are not as atomic as they should be. In particular, some actions have two external interactions, sometimes one with a channel and one with the client, sometimes two with channels. However, the simplified version differs from one with the proper atomicity only in unimportant details. The appendix gives a version of G with all the fussy details in place. We don’t give these details for the C and H protocols that follow, but content ourselves with the simplified versions in order to emphasize the important features of the protocols.
Figure 10.5 is a more detailed version of Figure 10.4, which shows all the actions and the flow of information between the sender and the receiver. State variables are given in bold, and the black guards on the transitions give the pre-conditions. The mark variable can be # when the receiver has recovered since a message was put; it reflects the fact that the message may be dropped.
Table 10.4 gives the state and actions of G. The magic parts, that is, those that touch non-local state, are boxed. The conjunct ¬ rec
s has been omitted from the guards of all the sender actions except recovers, and likewise for ¬ recr and the receiver actions.|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|
|
**put(m) |
msg = nil, |
msg := m, |
|
|
|
|
|
choose (i) |
msg ¹ nil,lasts = nil, i Î gs |
g s –:={j | j £ i},lasts := i, useds +:= áiñ |
*get(m) |
exists i such i Î gr |
g r –:={j | j £ i},lastr := i, sendrs(i, OK) |
|
|
send |
last s ¹ nil |
send sr(lasts, msg) |
|
|
|
|
|
*getAck(a) |
rcv rs(lasts, a) |
last s := nil,msg := nil |
sendAck |
exists i such i Ï gr |
optionally send rs(i, if i = lastr then OK else lost) |
|
|
**crash s |
|
rec s := true |
**crash r |
|
rec r := true |
|
|
*recover s |
rec s |
last s := nil,msg := nil, recs := false |
*recover r |
rec r,used r Êgs È useds |
last r := nil,mark := #, rec r := false |
|
|
shrink s(i) |
|
g s –:= {i} |
shrink r(i) |
i Ï gs, i ¹ lastsor mark = # |
g r –:= {i} |
|
|
grow s(i) |
i Ï useds,i Î gr or recr |
g s +:= {i} |
grow r(i) |
i Ï usedr |
g r +:= {i},usedr +:= {i} |
|
|
grow-used s(i) |
i Ï useds È gs,i Î usedr or recr |
used s +:= {i} |
cleanup |
last r ¹ lasts |
last r := nil |
|
|
|
|
|
unmark |
g s Í gr, lasts Îgr È {lastr,nil} |
mark := + |
|
In addition to meeting the spec S, this protocol has some other important properties:
• It makes progress;: regardless of prior crashes, provided both ends stay up and the channels don’t always lose messages, then if there’s a message to send it is eventually sent, and otherwise both parties eventually become idle, the sender because it gets an ack, the receiver because eventually cleanup makes mode = idle. Progress depends on doing enough grow actions, and in particular on completing the sequence grow
• It’s not necessary to do a stable storage operation ;for each message. Instead, the cost of a stable storage operation can be amortized over as many messages as you like. G has only two stable variables: used
s and usedr. Different implementations of G handle useds differently. To reduce the number of stable updates to usedr, refine G to divide usedr into the union of a stable usedr-s and a volatile usedr-v. Move a set of Is from usedr-s to usedr-v with a single stable update. The usedr-v becomes empty in recoverr; simulate this with growr(i) followed immediately by shrinkr(i) for every i in usedr-v.• The only state required for an idle agent is the stable variable used. All the other (volatile) state is the same at the end of a message transmission as at the beginning. The sender forgets its state in getAck, the receiver in cleanup, and both in recover. The shrink actions make it possible for both parties to forget the good sets. This is important because agents may need to communicate with many other agents between crashes, and it isn’t practical to require that an agent maintain some state for everyone with whom it has ever communicated.
• An idle sender doesn’t send any packets. An idle receiver doesn’t send any packets unless it receives one, because it sends an acknowledgement only in response to a packet. This is important because the channel resources shouldn’t be wasted.
We have constructed G with as much non-determinism as possible in order to make it easy to prove that different practical protocols implement G. We could have simplified it, for instance by eliminating unmark, but then it would be more difficult to construct an abstraction function from some other protocol to G, since the abstraction function would have to account for the fact that after a recover
r the mark variable is # until the next put. With unmark, an implementation of G is free to set mark back to + whenever the guard is true.10.5.1 Abstraction Function to D
The abstraction function is an essential tool for proving that the protocol implements the spec. But it is also an important aid to understanding what is going on. By studying what happens to the value of the abstraction function during each action of G, we can learn what the actions are doing and why they work.
Definitions
cur-q = {(msg, mark)} if msg
inflight
sr = {(i, m) Î ids(sr) | i Î gr and i ¹ lasts},old-q = the sequence of (M, Mark)’s gotten by turning
each (i, m) in inflight
inflight
rs = {lasts} if (lasts, OK) Î rs and lasts ¹ lastrNote that the inflights exclude elements that might still be retransmitted as well as elements that are not of interest to the destination. This is so the abstraction function can pair them with the # mark.
Abstraction function
|
q |
old-q + cur-q |
|
status |
(?, mark) if cur-q ¹ { } (a)(OK, +) if mode s = send and lasts = lastr (b)(OK, #) if mode s = send and lasts Î inflightrs (c)(lost, +) if mode s = send (d)and lasts Ï (gr È {lastr} È inflightrs) (lost, +) if mode s = idle (e) |
|
rec s/r |
rec s/r |
The cases of status are exhaustive. Note that we do not want (msg, +) in q if mode
s = send and lastss Ï gr, because in this case msg has been delivered or lost.We see that G simulates the q of D using old-q + cur-q, and that old-q is the leftover messages in the channel that are still good but haven’t been delivered, while cur-q is the message the sender is currently working on, as long as its identifier is not yet assigned or still good. Similarly, status has a different value for each step in the delivery process: still sending the message (a), normal ack (b), ack after a receiver crash (c), lost ack (d), or delivered ack (e).
10.5.2 Invariants
Like the abstraction function, the invariants are both essential to the proof and an important aid to understanding. They express a great deal of information about how the protocol is supposed to work. It’s especially instructive to see how the parts of the state that have to do with crashes (rec
s/r and mark) affect them.The first few invariants establish some simple facts about the used sets and their relation to other variables. (G2) reflects that fact that identifers move from g
s to useds one by one, (G3) the fact that unless the receiver is recovering, identifiers must enter usedr before they can appear anywhere else (G4) the fact that they must enter useds before they can appear in last variables or channels.If msg = nil then last
g
s Ç useds = { } (G2a)All elements of used
s are distinct. (G2b)used
r Ê gr (G3a)If ¬ rec
r then usedr Ê gs È useds (G3b)used
s Ê {lasts, lastr} – {nil} È ids(sr) È ids(rs) (G4)The next invariants deal with the flow of identifiers during delivery. (G5) says that each identifier tags at most one message. (G6) says that if all is well, g
s and lasts are such that a message will be delivered and acknowledged properly. (G7) says that an identifier for a message being acknowledged can’t be good.{m | (i = last
If mark = + and ¬ recs and ¬ recr then gs Í gr and lasts Î gr È {lastr, nil} (G6)
gr Ç ({lastr} È ids(rs)) = { } (G7)
Finally, some facts about the identifier lasts for the message the sender is trying to deliver. It comes later in the identifier ordering than any other identifier in sr (G8a). If it’s been delivered and is getting a positive ack, then neither it nor any other identifier in sr is in gr, but they are all in usedr (G8b). If it’s getting a negative ack then it won’t get a later positive one (G8c).
If lasts ¹ nil then
ids(sr) £ lasts (G8a)
and if lasts = lastr or (lasts,OK) Î rs then ({lasts} È ids(sr)) Ç gr = { } (G8b)
and ({lasts} È ids(sr)) Í usedr
and if (last
s, lost) Î ids(rs) then lasts ¹ lastr (G8c)10.5.3 Proof that G Implements D
This requires showing that every action of G simulates some sequence of actions of D which is the same externally. Since G has quite a few actions, the proof is somewhat tedious. A few examples give the flavor.
—recover
s: Mark msg and drop it unless it moves to old-q; mark and drop status.—get(m): For the change to q, first drop everything in old-q less than i. Then m is first on q since either i is the smallest I in old-q, or i = last
s and old-q is empty by (G8a). So D’s get(m) does the rest of what G’s does. Everything in old-q + cur-q that was £ i is gone, so the corresponding M’s are gone from q as required.We do status by the abstraction function’s cases on its old value. D says it should change to (OK, x) iff q becomes empty and it was (?, x). In cases (c-e) status isn’t (?, x) and it doesn’t change. In case (b) the guard i
Î gr of get is false by (G8b). In case (a) either i = lasts or not. If not, then cur-q remains unchanged by (G8a), so status does also and q remains non-empty. If so, then cur-q and q both become empty and status changes to case (b). Simulate this by umarking status if necessary; then D’s get(m) does the rest.—getAck(a): The q is unchanged because last
s = i Î ids(rs), so lasts Ï gr by (G7) and hence cur-q is empty, so changing msg to nil keeps it empty. Because old-q doesn’t change, q doesn’t either. We end up with status = (lost, +) according to case (e), as required by D. Finally, we must show that a agrees with the old value of status. We do this by the cases of status as we did for get:(a) Impossible, because it requires last
(b) In this case last
s = lastr, so (G8c) ensures a ¹ lost, so a = OK.(c) If a = OK we are fine. If a = lost drop status first.
(d) Since last
s Ï inflightrs, only (lasts, lost) Î rs is possible, so a = lost.(e) Impossible because last
s ¹ nil.—shrink
r: If recr then msg may be lost from q; simulate this by marking and dropping it, and likewise for status. If mark = # then msg may be lost from q, but it is marked, so simulate this by dropping it, and likewise for status. Otherwise the precondition ensures that lasts Î gr doesn’t change, so cur-q and status don’t. Inflightsr, and hence old-q, can lose an element; simulate this by dropping the corresponding element of q, which is possible since it is marked #.10.6 How C and H Implement G
We now proceed to give two practical protocols, the clock-based protocol C and the handshake protocol H. Each implements G, but they handle the good sets quite differently.
In C the good sets are maintained using time; to make this possible the sender and receiver clocks must be roughly synchronized, and there must be an upper bound on the time required to transmit a packet. The sender’s current time time
s is the only member of gs; if the sender has already used times then gs is empty. The receiver accepts any message with an identifier in the range (timer – 2e – d, timer + 2e), where e is the maximum clock skew from real time and d the maximum packet transmission time, as long as it hasn’t already accepted a message with a later identifier.In H the sender asks the receiver for a good identifier; the receiver’s obligation is to keep the identifier good until it crashes or receives the message, or learns from the sender that the identifier will never be equal to last
s.We begin by giving the abstraction functions from C and H to G, and a sketch of how each implements the magic actions of G, to help the reader in comparing the protocols. Careful study of these should make it clear exactly how each protocol implements G’s magic actions in a properly distributed fashion.
Then for each protocol we give a figure that shows the flow of packets, followed by a formal description of the state and the actions. The portion of the figures that shows messages being sent and acks returned is exactly the same as the bottom half of Figure 10.4 for G; all three protocols handle messages and acks identically. They differ in how the sender obtains good identifiers, shown in the top of the figures, and in how the receiver cleans up its state. In the figures for C and H we show the abstraction function to G in outline font.
Note that G allows either good set to grow or shrink by any number of Is through repeated grow or shrink actions as long as the invariants g
s Í gr and lasts Î gr È {lastr} are maintained in the absence of crashes. For C the increase actions simulate occurrences of several growr and shrinkr actions, one for each i in the set defined in the table. Likewise rcvrs(js, i) in H may simulate several shrinks actions.Abstraction functions to G
G |
C |
H |
||
|
used s |
{i | 0 £ i < times} È {sent} – {nil} |
used s (history) |
||
|
used r |
{i | 0 £ i < low} |
used r |
||
|
g s |
{time s} – {sent} |
{i | (j s, i) Î rs} |
||
|
g r |
{i | low < i and i < high} |
{i r} – {nil} |
||
|
mark |
# if last s Î gr and deadline = nil+ otherwise |
# if mode s = needI and gs Ë gr+ otherwise |
||
|
msg, last s/r, and recs/r are the same in G, C, and H |
|
|
||
|
sr |
sr |
the (I, M) messages in sr |
||
|
rs |
rs |
the (I, A) messages in rs |
||
Sketch of implementations
G |
C |
H |
grow s(i) |
tick (i) |
send rs(js, i) |
shrink s(i) |
tick (i'), i Î {times} – {sent} |
lose rs;(js, i) if the last copy is lostor rcv rs(js, i'), for each i Î gs – {i'} |
grow r(i) |
increase-high (i'), for eachi Î {i | high < i < i'} |
mode = idle and rcvsr(needI, *) |
shrink r(i) |
increase-low (i'), for eachi Î {i | low < i £ i'} |
rcv sr(ir, done) |
cleanup |
cleanup |
rcv sr(lastr, done) |
10.7 The Clock-Based Protocol C
This protocol is due to Liskov, Shrira, and Wroclawski [1991]. Figure 10.6 shows the state and the flow of information. Compare it with Figure 10.4 for G, and note that there is no flow of new identifiers from receiver to sender. In C the passage of time supplies the sender with new identifiers, and is also allows the receiver to clean up its state.
The idea behind C is to use loosely synchronized clocks to provide the identifiers for messages. The sender uses its current time for the next identifier. The receiver keeps track of low, the biggest clock value for which it has accepted a message: bigger values than this are good. The receiver also keeps a stable bound high on the biggest value it will accept, chosen to be larger than the receiver’s clock plus the maximum clock skew. After a crash the receiver sets low := high; this ensures that no messages are accepted twice.
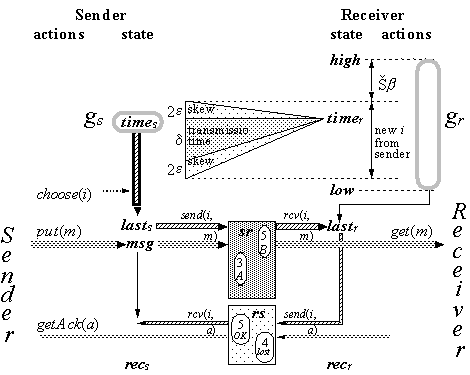
The sender’s clock advances, which ensures that it will get new identifiers and also ensures that it will eventually get past low and start sending messages that will be accepted after a receiver crash.
It’s also possible for the receiver to advance low spontaneously (by increase-low) if it hasn’t received a message for a long time, as long as low stays smaller than the current time – 2
e – d, where e is the maximum clock skew from real time and d is the maximum packet transmission time. This is good because it gives the receiver a chance to run several copies of the protocol (one for each of several senders), and make the values of low the same for all the idle senders. Then the receiver only needs to keep track of a single low for all the idle senders, plus one for each active sender. Together with C’s cleanup action this ensures that the receiver needs no storage for idle senders.If the assumptions about clock skew and maximum packet transmission time are violated, C still provides at-most-once delivery, but it may lose messages (because low is advanced too soon or the sender’s clock is later than high) or acknowledgements (because cleanup happens too soon).
Modes, types, packets, and the pattern of messages are the same as in G, except that the I set has a total ordering. The deadline variable expresses the assumption about maximum packet delivery time: real time doesn’t advance (by progress) past the deadline for delivering a packet. In a real implementation, of course, there will be some other properties of the channel from which the constraint imposed by deadline can be deduced. These are usually probabilistic; we deal with this by declaring a crash whenever the channel fails to meet its deadline.
|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|||
|
**put(m) |
msg = nil |
msg := m |
|
|
|
|||
|
choose (i) |
msg ¹ nil,lasts = nil, i=times, i¹sent |
sent := i, lasts := i,deadline := now+d |
*get(m) |
exists i such i Î (low..high) |
low := i, lastr := i,deadline := nil, sendrs(i, OK) |
|||
|
send |
last s ¹ nil |
send sr(lasts, msg) |
|
|
|
|||
|
*getAck(a) |
rcv rs(lasts, a) |
last s := nil,msg := nil |
sendAck |
exists i such i Ï (low..high) |
low := max(low, i),sendrs(i, if i = lastr then OK else lost ) if i = lasts then deadline := nil |
|||
|
**crash s |
|
rec s := true,deadline:= nil |
**crash r |
|
rec r := true,deadline:= nil |
|||
|
*recover s |
rec s |
last s := nil,msg := nil, recs := false |
*recover r |
rec r,high < timer – 2e |
last r := nil,low := high, high := timer + 2e + b, recr := false |
|||
|
|
|
|
increase-low (i) |
low < i £ timer– 2e – d |
low := i |
|||
|
|
|
|
increase-high (i) |
high < i £ timer+ 2e + b |
high := i |
|||
|
cleanup |
sent ¹ times |
sent := nil |
cleanup |
last r < timer– 2e – 2d |
last r := nil |
|||
|
tick (i) |
time s < i,|now – i| < e |
time s := i |
tick (i) |
time r < i,|now – i| < e, i + 2e < high or recr |
time r := i |
|||
|
progress (i) |
now < i, |i – times/r| < e,i < deadline or deadline=nil |
now := i |
|
|
|
|||
Table 10.5 gives the state and actions of C. The conjunct ¬ rec
s has been omitted from the guards of all the sender actions except recovers, and likewise for ¬ recr and the receiver actions.Note that like G, this version of C sends an ack only in response to a message. This is unlike H, which has continuous transmission of the ack and pays the price of a done message to stop it. Another possibility is to make timing assumptions about rs and time out the ack; some assumptions are needed anyway to make cleanup possible. This would be less practical but more like H.
Note that time
s and timer differ from real time (now) by at most e, and hence times and timer can differ from each other by as much as 2e. Note also that the deadline is enforced by the progress action, which doesn't allow real time to advance past the deadline unless someone is recovering. Both crashs and crashr cancel the deadline.About the parameters of C
The protocol is parameterized by three constants:
•
•
b = amount beyond timer + 2e to increase high•
e = maximum of |now – timer/s|These parameters must satisfy two constraints:
•
•
b > 0 so increase-high can be enabled. Aside from this constraint the choice of b is just a tradeoff between the frequency of stable storage writes (at least one every b, so a bigger b means fewer writes) and the delay imposed on recoverr to ensure that messages put after recoverr don’t get dropped (as much as 4e + b, because high can be as big as timer + 2e + b at the time of the crash because of (e), and timer – 2e has to get past this via tickr before recoverr can happen, so a bigger b means a longer delay).10.7.1 Invariants
Mostly these are facts about the ordering of various time variables; a lot of x
¹ nil conjuncts have been omitted. Nothing being sent is later than times (C1). Nothing being acknowledged is later than low, which is no later than high, which in turn is big enough (C2). Nothing being sent or acknowledged is later than lasts (C3). The sender’s time is later than low, hence good unless equal to sent (C4).last
last
r £ low £ high (C2a)ids(rs)
£ low (C2b)If ¬ rec
r then timer + 2e £ high (C2c)ids(sr)
£ lasts (C3a)last
r £ lasts (C3b){i | (i, OK)
Î rs} £ lasts (C3c)low
£ times (C4)If a message is being sent but hasn’t been delivered, and there hasn’t been a crash, then deadline gives the deadline for delivering the packet containing the message (based on the maximum time for a packet that is being retransmitted to get through sr), and it isn’t too late for it to be accepted (C5).
If deadline
¹ nil thennow < last
low < last
s (C5b)An identifier getting a positive ack is no later than low, hence no longer good (C6). If it’s getting a negative ack, it must be later than the last one accepted (C7).
If (last
If (last
s, lost) Î rs then lastr < lasts (C7)10.8 The Handshake Protocol H
This is the standard protocol for setting up network connections, used in TCP, ISO TP-4, and many other transport protocols. It is usually called three-way handshake, because only three packets are needed to get the data delivered, but five packets are required to get it acknowledged and all the state cleaned up (Belsnes [1976]).
As in the generic protocol, when there are no crashes the sender and receiver each go through a cycle of modes, the sender perhaps one ahead. For the sender, the modes are idle, needI, send; for the receiver, they are idle, accept, and ack. In one cycle one message is sent and acknowledged by sending three packets from sender to receiver and two from receiver to sender, for a total of five packets. Table 10.6 summarizes the modes and the packets that are sent.
The modes are derived from the values of the state variables j and last:
mode
Figure 10.7 shows the state, the flow of identifiers from the receiver to the sender at the top, and the flow of done information back to the receiver at the bottom so that it can clean up. These are sandwiched between the standard exchange of message and ack, which is the same as in G (see Figure 10.4).
Intuitively, the reason there are five packets is that:
• One round-trip (two packets) is needed for the sender to get from the receiver an I (namely i
• One round-trip (two packets) is then needed to send and ack the message.
|
Sender |
|
Receiver |
||||||||||||||||||
|
mode |
send |
advance on |
packet |
advance on |
send |
mode |
||||||||||||||
|
idle |
see idle below |
put ,to needI |
|
|
(i, lost) when |
idle |
||||||||||||||
|
needI |
(needI, j s) repeatedly |
|
(needI, j) |
(needI, j) arrives, |
|
|
||||||||||||||
|
|
|
(j s, i) arrives,to send |
(j, i) |
|
(j r, ir)repeatedly |
accept |
||||||||||||||
|
send |
(last s, m)repeatedly |
|
(i, m) ® |
(i r, m) arrives,to ack (ir, done) arrives, to idle |
|
|
||||||||||||||
|
|
|
(last s, a ) arrives, to idle |
(i, a) ¬ |
|
(last r, OK)repeatedly |
ack |
||||||||||||||
|
idle |
(i, done) when |
|
(i, done) |
(last r, done) arrives,to idle |
|
|
||||||||||||||
|
needI or send |
(i, done) when to force receiver to idle |
|
|
|
|
|
||||||||||||||
• A final done packet from the sender informs the receiver that the sender has gotten the ack. The receiver needs this information in order to stop retransmitting the ack and discard its state. If the receiver discards its "I got the message" state before it knows that the sender got the ack, then if the channel loses the ack the sender won’t be able to find out that the message was actually received, even though there was no crash. This is contrary to the spec S. The done packet itself needs no ack, because the sender will also send it when idle and hence can become idle as soon as it sees the ack.
We introduce a new type:
J, an infinite set of identifiers that can be compared for equality.
The sender and receiver send packets to each other. An I or J in the first component is there to identify the packet for the destination. Some packets also have an I or J as the second component, but it does not identify anything; rather it is being communicated to the destination for later use. The (i, a) and (i, done) packets are both often called ’close’ ;packets in the literature.
The H protocol has the same progress and efficiency properties as G, and in addition, although the protocol as given does assume an infinite supply of Is, it does not assume anything about clocks.
It’s necessary for a busy agent to send something repeatedly, because the other end might be idle and therefore not sending anything that would get the busy agent back to idle. An agent also has a set of expected packets, and it wants to receive one of these in order to advance normally to the next mode. To ensure that the protocol is self-stabilizing ;after a crash, both ends respond to an unexpected packet containing the identifier i by sending an acknowledgement: (i, lost) or (i, done). Whenever the receiver gets done for its current I, it becomes idle. Once the receiver is idle, the sender advances normally until it too becomes idle.
Table 10.7 gives the state and actions of H. The conjunct ¬ rec
s has been omitted from the guards of all the sender actions except recovers, and likewise for ¬ recr and the receiver actions.10.8.1 Invariants
Recall that ids(c) is {i | (i, *)
Î c}. We also define jds(c) = {j | (j, *) Î c or (*, j) Î c}.Most of H’s invariants are boring facts about the progress of I’s and J’s from used sets through i/j
s/r to lasts/r. We need the history variables useds and seen to express some of them. (H6) says that there’s at most one J (from a needI packet) that gets assigned a given I. (H8) says that as long as the sender is still in mode needI, nothing involving ir has made it into the channels.|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
|
**put(m) |
msg = nil, |
msg := m, |
|
|
|
|
|
exists j such |
j s := j,j-used +:= {j} |
|
|
|
|
requestI |
j s ¹ nil,lasts = nil |
send sr(needI, js) |
assignI (j,i) |
rcv sr(needI, j),ir = lastr = nil, i Ï usedr |
j r := j, ir := i,usedr +:= i, seen +:= {(j, i)} |
|
choose (i) |
last s = nil,rcvrs(js, i) |
j s := nil, lasts := i,useds +:= áiñ |
sendI |
j r ¹ nil |
send rs(jr, ir) |
|
send |
last s ¹ nil |
send sr(lasts, msg) |
*get(m) |
exists i such i = ir |
j r := ir := nil,lastr := i, sendrs(i, OK) |
|
|
|
|
sendAck |
last r ¹ nil |
send rs(lastr, OK) |
|
*getAck(a) |
rcv rs(lasts, a) |
if a = OK then msg := lasts := nil |
bounce |
exists i such i ¹ ir, i ¹ lastr |
send rs(i, lost ) |
|
bounce (j, i) |
rcv rs(j, i),j ¹ js, i ¹ lasts or rcvrs(i, OK) |
send sr(i, done) |
cleanup (i) |
rcv sr(i, done),i = ir or i = lastr |
j r := ir := nil,lastr := nil |
|
**crash s |
|
rec s := true |
**crash r |
|
rec r := true |
|
*recover s |
rec s |
msg := nil,js := lasts := nil, recs := false |
*recover r |
rec r |
j r := ir := nil,lastr := nil, recr := false |
|
grow- |
|
j-used +:= {j} |
grow- |
|
used r +:= {i} |
j-used
Ê {js, jr} – {nil} È jds(sr) È jds(rs) (H1)used
r Ê {ir, lastr} – {nil} È useds È {i | (*, i) Î rs} È ids(sr) È ids(rs) (H2)used
s Ê {lasts, lastr} – {nil} È ids(sr) È ids(rs) (H3)If (i, done)
Î sr then i ¹ lasts (H4)If i
r ¹ nil then (jr, ir) Î seen (H5)If (j, i)
Î seen and (j’, i) Î seen then j = j’ (H6)If (j, i)
Î rs then (j, i) Î seen (H7)If j
s = jr ¹ nil then (ir, *) Ï sr and (ir, done) Ï rs (H8)10.8.2 Progress
We consider first what happens without failures, and then how the protocol recovers from failures.
If neither partner fails, then both advance in sync through the cycle of modes. The only thing that derails progress is for some party to change mode without advancing through the full cycle of modes that transmits a message. This can only happen when the receiver is in accept mode and gets (i
r, done), as you can see from Table 10.6. This can only happen if the sender got a packet containing ir. But if the receiver is in accept, the sender must be in needI or send, and the only thing that’s been sent with ir is (js, ir). The sender goes to or stays in send and doesn’t make done when it gets (js, ir); in either of these modes, so the cycling through the modes is never disrupted as long as there’s no crash.If either partner fails and then recovers, the other becomes idle rather than getting stuck; in other words, the protocol is self-stabilizing. Why? When the receiver isn’t idle it always sends something, and if that isn’t what the sender wants, the sender responds done, which forces the receiver to become idle. When the sender isn’t idle it’s either in needI, in which case it will eventually get what it wants, or it’s in send and will get a negative ack and become idle. In more detail:
The receiver bails out when the sender crashes because
• the sender forgets i
• if the receiver isn’t idle, it keeps sending (j
r, ir) or (lastr, OK),• the sender responds with (i
r/lastr, done) when it sees either of these, and• the receiver ends up in idle whenever it receives this.
The sender bails out or makes progress when the receiver crashes because
• If the sender is in needI, either
—it gets (j
—it gets (j
s, ir) from the post-crash receiver and proceeds normally.• If the sender is in send it keeps sending (last
s, msg),—the receiver has last
r = nil ¹ lasts, so it responds (lasts, lost), and—when the sender gets this it becomes idle.
An idle receiver might see an old (needI, j) with j
¹ js and go into accept with jr ¹ js, but the sender will respond to the resulting (jr, ir) packets with (ir, done), which will force the receiver back to idle. Eventually all the old needI packets will drain out. This is the reason that it’s necessary to prevent a channel from delivering an unbounded number of copies of a packet.10.9 Finite Identifiers
|
Name |
Guard |
Effect |
|
recycle (i)for G |
i Ï gs È gr È {lasts, lastr}È ids(sr) È ids(rs) |
used s –:= {i},usedr –:= {i} |
|
recycle (i)for H |
i Ï {lasts, ir, lastr}È {i | (*, i) Î rs} È ids(sr) È ids(rs) |
used s –:= {i},usedr –:= {i}, seen –:= {j | (j, i) Î seen | (j, i)} |
|
recycle-j (j)for H |
j Ï {js, jr} È jds(sr) È jds(rs) |
used-j –:= {j},seen –:= {i | (j, i) Î seen | (j, i)} |
So far we have assumed that the identifier sets I and J are infinite. Practical protocols use sets that are finite and often quite small. We can easily extend G to use finite sets by adding a new action recycle(i) that removes an identifier from used
s and usedr so that it can be added to gr again. As we saw in Section 10.1, when we add a new action the only change we need in the proof is to show that it maintains the invariants and simulates something in the spec. The latter is simple: recycle simulates no change in the spec. The former is also simple: we put a strong enough guard on recycle to ensure that all the invariants still hold. To find out what this guard is we need only find all the invariants that mention useds or usedr, since those are the only variables that recycle changes. Intuitively, the result is that an identifier can be recycled if it doesn’t appear anywhere else in the variables or channels.Similar observations apply to H, with some minor complications to keep the history variable seen up to date, and a similar recycle-j action. Table 10.8 gives the recycle actions for G and H.
How can we implement the guards on the recycle actions? The tricky part is ensuring that i is not still in a channel, since standard methods can ensure that it isn’t in a variable at the other end. There are three schemes that are used in practice:
• Use a fifo channel. Then a simple convention ensures that if you don’t send any i
• Assume that packets in the channel have a maximum lifetime once they have been sent, and wait longer than that time after you stop sending packets containing i.
• Encrypt packets on the channel, and change the encryption key. Once the receiver acknowledges the change it will no longer accept packets encrypted with the old key, so these packets are in effect no longer in the channel.
For C we can recycle identifiers by using time modulo some period as the identifier, rather than unadorned time. Similar ideas apply; we omit the details.
10.10 Conclusions
We have given a precise specification S of reliable at-most-once message delivery with acknowledgements. We have also presented precise descriptions of two practical protocols (C and H) that implement S, and the essential elements of proofs that they do so; the handshake protocol H is used for connection establishment in most computer networking. Our proofs are organized into three levels: we refine S first into another specification D that delays some of the decisions of S and then into a generic implementation G, and finally we show that C and H both implement G. Most of the work is in the proof that G implements D.
In addition to complete expositions of the protocols and their correctness, we have also given an extended example of how to use abstraction functions and invariants to understand and verify subtle distributed algorithms of some practical importance. The example shows that the proofs are not too difficult and that the invariants, and especially the abstraction functions, give a great deal of insight into how the implementations work and why they satisfy the specifications. It also illustrates how to divide a complicated problem into parts that make sense individually and can be attacked one at a time.
References
Abadi, M. and Lamport, L. (1991), The Existence of Refinement Mappings, Theoretical Computer Science 82 (2), 253-284.
Belsnes, D. (1976), Single Message Communication, ieee Trans. Communications com-24, 2.
Lampson, B., Lynch, N., and Søgaard-Andersen, J. (1993), Reliable At-Most-Once Message Delivery Protocols, Technical Report, mit Laboratory for Computer Science, to appear.
Liskov, B., Shrira, L., and Wroclawski, J. (1991), Efficient At-Most-Once Messages Based on Synchronized Clocks, acm Trans. Computer Systems 9 (2), 125-142.
Lynch, N. and Vaandrager, F. (1993), Forward and Backward Simulations, Part I: Untimed Systems, Technical Report, mit Laboratory for Computer Science, to appear.
Appendix
For reference we give the complete protocol for G, with every action as atomic as it should be. This requires separating the getting and putting of messages, the sending and receiving of packets, the sending and receiving of acks, and the getting of acks. As a result, we have to add buffer queues buf
s/r for messages at both ends, a buffer variable ack for the ack at the sender, and a send-ack flag for positive acks and a buffer nack-buf for negative acks at the receiver.The state of the full G is:
used
The abstraction function to D is:
|
q |
the elements of buf r paired with + |
|
|
+ old-q + cur-q |
|
|
+ the elements of buf s paired with + |
|
status |
(?, +) if buf s ¹ emptyelse (?, mark) if cur-q ¹ { } (a)(?, +) if mode s = send, lasts = lastr, bufr ¹ { } (b)(OK, +) if mode s = send, lasts = lastr, bufr = { } (c)(OK, #) if mode s = send and lasts Î inflightrs (d)(lost, +) if mode s = send (e)and lasts Ï (gr È {lastr} È inflightrs) (ack, +) if mode s = idle (f) |
|
rec s/r |
rec s/r |
|
Name |
Guard |
Effect |
Name |
Guard |
Effect |
||||
|
**put(m) |
|
append m to buf s |
|
|
|
||||
|
prepare (m) |
msg = nil,m first on bufs, g s Í gr or recr |
buf s:=tail (bufs), msg := m,mark := + |
|
|
|
||||
|
choose (i) |
msg ¹ nil,lasts = nil, i Î gs |
g s –:= {j | j £ i},lasts := i, useds +:= áiñ |
|
|
|
||||
|
send sr(i, m) |
i = lasts ¹ nilm = msg |
|
rcv sr(i, m) |
|
if i Î gr then append m to bufr,sendAck := false, gr –:= {j | j £ i}, lastr := i, else if i Ï gr È {lastr} then optionally nack-buf +:= áiñ else if i = lastr then sendAck :=true |
||||
|
|
|
|
*get(m) |
m first on bufr |
if buf r = ámñ thensendAck := true, bufr :=tail (bufr) |
||||
|
rcv rs(i, a) |
|
if i = last s thenack := a, msg := nil, lasts := nil |
send rs(i, OK) send rs(i, lost) |
i = lastr, sendAcki first on nack-buf |
optionally nack-buf := |
||||
|
*getAck(a) |
msg = nil,bufs = empty, ack = a |
ack := lost |
|
|
|
||||
|
**crash s |
|
rec s := true |
**crash r |
|
rec r := true |
||||
|
*recover s |
rec s |
last s := nil,msg := nil, bufs := á ñ, ack := lost, recs := false |
*recover r |
rec r,used r Êgs È useds |
last r := nil,mark := #, bufr:=á ñ, nack-buf:=á ñ, recr:=false |
||||
|
shrink s(i) |
|
g s –:= {i} |
shrink r(i) |
i Ï gs, i ¹ lastsor mark = # |
g r –:= {i} |
||||
|
grow s(i) |
i Ï used,i Î gr or recr |
g s +:= {i} |
grow r(i) |
i Ï usedr |
g r +:= {i},used +:= {i} |
||||
|
grow-used s(i) |
i Ï used È gs,i Î usedr or recr |
used +:= {i} |
cleanup |
last r ¹ lasts |
last r := nil |
||||
|
|
|
|
unmark |
g s Í gr, lasts Îgr È {lastr, nil} |
mark := + |
||||