This document was made by OCR
from a scan of the technical report. It has not been edited or proofread and is
not meant for human consumption, but only for search engines. To see the
scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL
that got you here.
On-line Data Compression
in a Log-structured File System
Michael Burrows
Charles Jerian
Butler Lampson
Timothy Mann
April 15, 1992
This report appeared
in the proceedings of the Fifth International Conference on Architechural Support for
Programming Languages and Operating Systems (ASPLOS-V),
12-15 October, 1992, published by ACM Press.
c~ Digital Equipment Corporation
1992
This work may not be
copied or reproduced in whole or in part for any commercial purpose. Permission
to copy in part without payment of fee is granted for nonprofit educational and research purposes provided that all
such whole or partial copies include the
following: a notice that such copying is by permission of the Systems Research
Center of Digital Equipment Corporation in Palo Alto, California; an
acknowledgment of the authors and individual contributors to the work; and all applicable portions of the copyright notice.
Copying, reproducing, or republishing for
any other purpose shall require a license with payment of fee to the Systems Research
Center. All rights reserved.
We have incorporated on-line data
compression into the low levels of a log-structured file system (Rosenblum’s Sprite
LFS). Each block of data or
meta-data is compressed as it is written to the disk and decompressed as it is read. The log-structuring overcomes the
problems of allocation and fragmentation for variable-sized blocks. We
observe compression factors ranging from 1.6
to 2.2, using algorithms running from 1.7 to 0.4 MBytes per second in
software on a DECstation 5000/200. System performance is degraded by a few percent for normal activities
(such as compiling or editing), and as much as a factor of 1.6 for file
system intensive operations (such as copying multi-megabyte files).
Hardware compression devices mesh well with this
design. Chips are already available that
operate at speeds exceeding disk transfer rates, which indicates that hardware
compression would not only remove the performance degradation we observed, but might well increase
the effective disk transfer rate beyond that obtainable from a system
without compression.
Contents
1
Introduction 1
2
Sprite LFS 3
3
Adding compression to LFS 4
3.1 Logical and physical disk space ..................4
3.2 Reading a logical block ......................4
3.3 Writing to the log .........................6
3.4 Crash recovery ...........................8
3.5 Compression
block size ......................9
3.6 Free
space .............................9
3.7 File-specific compression .....................10
4
Compression algorithms 10
5
LFS and compression hardware 12
5.1 System
changes ..........................12
5.2 Compression hardware .......................13
6 Performance of
prototype 14
7
Comparison with other work 16
8
Summary 18
Acknowledgements 18
References 20
1 Introduction
Building a file system that compresses the
data it stores on disk is clearly an attractive
idea. First, more data would fit on the disk. Also, if a fast hardware data
compressor could be put into the data path to disk, it would increase the effective disk transfer rate by the compression
factor, thus speeding up the system. Yet
on-line data compression is seldom used in conventional file systems, for two reasons.
First, compression algorithms do
not provide uniform compression on all data. When a file block is overwritten,
the new data may be compressed by a different amount from the data it supersedes. Therefore the file system cannot
simply overwrite the original blocks—if the new data is larger than the old, it
must be written to a place where there is
more room; if it is smaller, the file system must either find some use for the freed space or see it
go to waste. In either case, disk space tends to become fragmented,
which reduces the effective compression.
|
input block size
(bytes)
|
compression ratio
(output size/input size)
|
|
1K
|
68%
|
|
2K
|
63%
|
|
4K
|
59%
|
|
8K
|
55%
|
|
16K
|
53%
|
|
32K
|
51%
|
The file progc from the Calgary
Compression Corpus [3] was compressed using various block sizes. The file contains 39611 bytes of C
source. The entire file was compressed, one block at a time. The
compression algorithm is described below in Section 4 as Algorithm 2.
Table 1: An example of improved compression with increased
block size.
Second,
the best compression algorithms are adaptive—they use patterns discovered in one part of a block
to do a better job of compressing information in other parts [3]. These algorithms work better on
large blocks of data than on small blocks.
Table 1 shows the variation in compression ratio with block size for a simple
adaptive compression algorithm. The details vary for different compression algorithms and different data, but the
overall trend is the same—larger blocks make for better compression.







 file block A
file block A
Figure1:Simplified
viewofLFS’slog.
AAAA
However,
it is difficult to arrange for sufficiently large blocks of data to be compressed all at once. Most file systems use block
sizes that are too small for good
compression, and increasing the block size would waste disk space in fragmentation. Compressing multiple blocks at a time
seems difficult to do efficiently, since adjacent blocks are often not
written at the same time. Compressing whole files
would also be less than ideal, since in many systems most files are only a few kilobytes
[2].
In
a log-structured file system, the main data structure on disk is a sequentially
written log. All new data, including
modifications to existing files, is written to the end of the log. This
technique has been demonstrated by Rosenblum and Ousterhout in a system called Sprite LFS [9]. The main goal of LFS was
to provide improved performance by eliminating disk seeks on writes. In
addition, LFS is ideally suited for adding
compression—we simply compress the log as it is written to disk. No blocks are overwritten, so we do not
have to make special arrangements when new data does not compress as
well as existing data. Because blocks are written
sequentially, the compressed blocks can be packed tightly together on disk, eliminating fragmentation. Better still, we can
choose to compress blocks of any size
we like, and if many related small files are created at the same time, they will be compressed together, so any similarities
between the files will lead to better compression. We do, however, need
additional bookkeeping to keep track of where compressed blocks fall on
the disk.
The remainder of this paper describes the relevant features of Sprite
LFS, the changes needed to introduce
compression, and the performance of our modified
system using simple software compression routines. We argue that suitable hardware
compression devices can be readily obtained or constructed.
2 Sprite LFS
Sprite LFS places all
file data and almost all meta-data (for example, directory information) in a sequentially written log. The file
system data structures allow any block of an existing file to be located
quickly in the log. For a full description see Rosenblum and Ousterhout’s paper
[9].
The
log is stored in a chain of fixed-size segments, each of which is a
contiguous array of disk sectors. The system keeps track of the current
segment, which is the segment containing the current end of the log. When the current segment
becomes full, the system picks an unused
segment, links it onto the end of the chain, and makes it the current segment.
As
files are deleted and rewritten, some of the data in the log becomes obsolete. The space occupied by this data is reclaimed by the segment
cleaner, which is analogous to a copying garbage collector in a programming
language run-time system. The cleaner chooses segments and scans them to
determine which blocks are still in use, appending them to the log in the usual
manner. The cleaned segments are then unlinked from the log and made available
for reuse.
Some of the blocks
written to the log contain file data, while others contain meta-data of various kinds, and the segment
cleaner must be able to tell which is which. To do this, it uses summary
blocks, which also appear in the log. These blocks contain a small amount
of identifying information for each item written to the log. At least one
summary block is written for each segment, and additional blocks are used if the first is not large enough
to describe all the data being written. The summary blocks in a segment
are linked together to form a list.
Inodes are
an important type of meta-data. Like a UNIX1 inode, a Sprite LFS inode contains information
about its associated file, including pointers to data blocks contained in the file. Whenever a file is
modified, an updated copy of its inode is placed in the log. To avoid
fragmentation, LFS places several inodes together
in one block when it can. LFS maintains an inode map, which allows the current copy of any inode to be found quickly. The
inode map is also written to the log.
When LFS writes data to the log,
it first builds a list of elements. Each element
represents a number of disk blocks, and
the order of the elements gives the order
in which the blocks will appear on disk. Each element is a logical unit, such
as a
summary block, a block of inodes, or file
data. It is only when an element is added
to the list that the system can tell
where the data in the element will fall on the disk.
Periodically, LFS writes a checkpoint,
by flushing the current state of in‑
 1UNIX is a registered trademark of UNIX System Laboratories,
Inc.
1UNIX is a registered trademark of UNIX System Laboratories,
Inc.
memory data structures to the log and writing a
pointer to the end of the log in a fixed
location on disk. When recovering from crashes, LFS restores the file system state as of the last checkpoint, and then rollsforward
by following the chain of log segments written subsequently.
3 Adding compression to LFS
3.1
Logical and physical disk space
As with the original
Sprite LFS, our modified system divides the physical disk into fixed-sized segments chained
together to form a log. However, because of compression, each segment can
contain more user data than its physical size might suggest. Accordingly, we
allocate space within the segment in two ways: logical and physical. The physical
space represents real disk blocks, while the logical space represents the space that
would have been occupied by the data if it were not compressed.
As
each kilobyte of data is added to a segment, it occupies a kilobyte of logical space, but may occupy less
physical space. A segment is declared full when either its physical or its logical space
is exhausted. (If logical space becomes full first, some physical space is wasted. So
logical space should be larger than physical space by a factor greater than the maximum compression expected.)
Logical
space is subdivided into compression blocks, which are the units of compression and decompression. A
logical disk address consists of a segment number, a compression
block number within the segment, and a sector number within the
compression block. We chose a physical segment size of 512 KBytes and a maximum
compression factor of four, so our logical segment size was 2 MBytes. Our
compression blocks are 16 KBytes, and our sector size is 512 bytes. Thus, our
logical disk addresses fit easily in a 32-bit word:
|
segment (20 bits)
|
compression block (7 bits)
|
sector (5 bits)
|
3.2 Reading a logical
block
Most of the modified
file system deals exclusively in logical disk addresses. For example, the disk addresses used
by the file system cache are logical, and so are the disk addresses placed in inodes. Physical addresses
are needed only by modules at the lowest level of the file system.

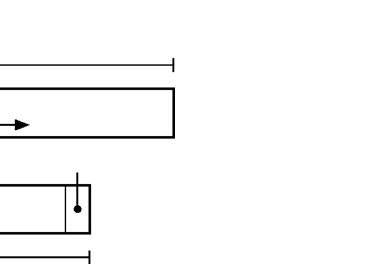




 512 KByte physical segment
512 KByte physical segment
Figure 2: Logical and
physical views of a segment.
The module that
reads a disk block given its logical address needs a way to find the physical
address of the compressed bytes. We keep a logical block map for each segment, which is simply an array indexed
by compression block number, whose
entries are the physical byte addresses of the blocks relative to the start of the
segment. The block map is constructed in memory as the segment is being
compressed, and written to the end of the segment when the segment is full. The
maps are needed for all file reads, so they
are cached in memory whenever possible. Because our logical segments
contain 128 compression blocks and our physical segments are 512 KBytes, our block maps each contain 128 four-byte
entries, which exactly fills one 512-byte disk sector. (The entries
could be reduced to two bytes each by restricting compression blocks to begin
on eight byte boundaries within the segment, but we did not implement this
optimization in our prototype.) The
procedure for finding the compressed data associated with a logical address is as
follows:
1. Extract the segment number from
the logical address. Use it to find the logical
block map for the segment.
2. Extract the compression block
number from the address. Use it to index the logical block map. This yields the physical byte offset of the
compressed data within the segment.
3. Examine the next entry in the map, to find the start
of the next block. This determines how much data should be read from the disk.
4. Read the compressed data from the
disk and decompress it.
5. Extract the sector
number from the logical address. Use it to identify the desired sector within the decompressed block.
Unfortunately,
this procedure reads and decompresses a full compression block even if the caller wanted only
some smaller unit, such as a file system block or a physical sector. We alleviate this problem by caching
the entire decompressed block in memory,
rather than just caching the requested sectors. The data could be placed
in the file system buffer cache, but for simplicity in our prototype, we cached the last decompressed block within the read
routine. Sprite LFS reads files sequentially in 4 KByte units, so this
simple caching strategy typically achieves three hits for each 16 KByte
compression block when reading large files.
When
the file system is reading non-sequentially, the additional time to read a full compression block cannot be
hidden by caching. Fortunately, this time is small compared to the rotational latency. The time needed to
decompress the full block in software is
several milliseconds; it would be much smaller if decompression were
implemented in hardware.
3.3 Writing to the log
Conceptually, it is
simple to write compressed data to the log. As LFS constructs its element list,
it can compress the data into a buffer, one compression block at a time. When there is no more data to
add to the list, or when logical or physical segment space is exhausted, it writes the buffer to disk and
updates the logical block map for the segment. In practice, however, the design
was more complicated.
In Sprite LFS, the
contents of certain kinds of element, such as inode blocks, are allowed to change even after they are added
to the element list; we will call these variable elements. For
example, when LFS puts the first inode in a segment, it allocates an empty inode block and places it on the element list. When
more inodes are added to the segment,
they are placed in this inode block. Eventually, it may become full, at which point another block is allocated for inodes.
Thus, an inode block may have inodes added to it long after it has been
placed on the element list. A similar
strategy is used for summary blocks—this technique allows LFS to make
better use of disk space when allocating small data structures.
In an unmodified
LFS, these variable elements present no difficulty; the contents of elements can be changed freely until the
segment is written to disk, as long
as their size does not change.
However, in our system, the data for each element must be known before the element
can be compressed, and compression must take place early enough to decide which elements fit
into the current segment. We know of two
ways to accommodate variable elements in a compressed LFS.
One technique is to
delay compressing variable elements until just before the segment is written to
disk. Enough physical space must be reserved to hold the variable elements, assuming the worst-case
compression ratio (i.e. that they cannot be compressed at all). With this approach, there is little benefit in
compressing the variable elements, since the space saved cannot easily
be used.
A second technique
is to delay compressing all elements as long as possible, allowing variable elements to be changed freely
until they are compressed, but not
afterwards. We do not compress elements as they are added; instead, we reserve enough physical space for each element to
accommodate the worst-case compression
ratio, until we can no longer be sure the next element will fit into the
physical segment. Then we compress all the elements, correct the amount of physical space remaining to reflect the actual
compression achieved, and mark the elements as no longer variable. When
an inode block is compressed, for example, it
can be marked as full so that no further inodes will be added to it. A new
block will automatically be allocated if needed.
The following pseudo-code illustrates the
action taken for each element e lem, containing size (elem) bytes. The worst case function returns the largest number of bytes that may be needed to
represent the data when compressed.
if (size(elem) > logical_space_left) { goto
segment_full
}
if (worst
_case(elem) > phys _space _left) {
compress all elements not yet
compressed increase phys _space_left by bytes saved mark inode blocks
full
if (worst _case(elem) > phys _space _left) { goto
segment_full
}
}
add elem to
element list, without compression
reduce logical_space_left by size (elem)
This
approach is less general than the first, since it works only if the code that modifies variable elements
can be told to stop doing so at an arbitrary point; however, it does allow variable elements to be
compressed.
Both the summary
blocks and inode blocks of Sprite LFS could be handled using either technique. As a matter of expediency, we used the first
technique for
summary blocks and the second for
inode blocks, and we chose not to compress summary
blocks. These choices worked out fairly well: there are few summary blocks per segment, so little compression is lost,
and crash recovery is not adversely affected (see Section 3.4). Inode
blocks tend to be less full than in unmodified LFS—two or three blocks might be allocated per segment where only one
would have been used before—but little physical space is wasted because
a partially-empty block compresses exceedingly well. However, programs that
read many inodes (such as the file tree walker find) do not perform as
well; see Section 6 below for details.
A
third technique for dealing with variable elements is to eliminate them. We could have modified Sprite LFS to
fill summary blocks and inode blocks completely before adding them to the element list. This would have been difficult,
however, because the logical disk address of a data block is not known until it
is added to the element list, and the
current LFS implementation needs to know the addresses of summary blocks and inode blocks as it fills
them in, for use as pointers in other data
structures. Also, LFS needs to know that the summary block it is filling will
fit into the current segment, not be spilled over into the next one. Therefore
we chose not to take this approach in our prototype.
3.4 Crash recovery
Our changes introduce
a new problem in crash recovery. The system could crash after a segment has been written, but before the
logical block map has been committed to
disk. One might view this as an argument for writing the logical block
map first, at the start of the segment. However, LFS often fills a segment using a small number of partial writes—these
are used when it is necessary to commit
data to disk, but the data does not fill an entire segment. So, on successive partial
writes the segment’s block map would be updated in place, and could therefore be lost in a crash. Alternatively, we
could allocate a new block map for each partial segment written, but
this would consume additional disk space and complicate the process of reading
and parsing the maps.
Fortunately, this
problem is easy to solve. We maintain the invariant that all segments on the
disk have a valid logical block map on disk, except possibly the current segment. When the file system examines
the disk after a crash, it must first read the current segment,
decompress it from the beginning, and reconstruct the logical block map. This action is similar to rolling forward from a
checkpoint.
We do not compress
the checkpoint areas or the summary blocks. Together, these blocks contain enough information for LFS to find the end of the
log during recovery: we modified the
segment cleaner to read segments without using the
block
map in order to exercise this algorithm. 3.5 Compression block size
We would like to compress data in
large blocks, but there are reasons for choosing smaller blocks.
First, when reading bytes from the disk,
decompression must start from the beginning
of a compressed block. Thus, the mean latency for reading a randomly chosen
byte on the disk is increased by the time to read the block from the disk and decompress it. A 16 KByte block seems to be a
reasonable choice, since it is large
enough to allow the compression algorithm to obtain most of the compression available, but small enough that it adds only a
few milliseconds to the transfer time. In software on a DECstation
5000/2002, the decompression time is 9 ms for the fastest algorithm
we tried; in hardware, decompression would be faster than the disk transfer,
and could be overlapped with it more easily.
A second issue is that
applications often commit small amounts of data to disk, resulting in poor
compression. The obvious way to overcome this problem is to employ a small amount of non-volatile memory to
postpone compression until more data is
available. Alternatively, one can ignore the problem and write the data
immediately, because the segment cleaner will later combine the data from
adjacent writes to form a full-sized compression block. This is similar
to the strategy used in unmodified LFS to
recover unused space left in inode and summary blocks after small
amounts of data have been committed.
The cleaner saves
space in other minor ways too. In our system, when two compression blocks are
written together, no gap need be left between them. But when two blocks are forced to disk independently, the second must start
on a sector boundary to avoid the danger of damaging previously written data.
This causes fragmentation that is removed later by the segment cleaner.
3.6
Free space
One problem with
using compression in a file system is that it leaves the naive user open to surprises. For one thing, it is no longer
obvious how to report the amount of space remaining on the disk! It seems best
to report the amount of data that could be
put on the disk assuming worst-case compression (i.e. no compression at all),
so that the user is more likely to be agreeably surprised than upset.
A more worrying problem is that
actions that do not consume disk space in conventional file systems may do so when compression is
used. For example, if a
 2DECstation is a trademark of Digital Equipment
Corporation
2DECstation is a trademark of Digital Equipment
Corporation
block in a file is overwritten,
the new data may not compress as much as the old data. When compression is used, such operations
cannot be allowed when the disk is full.
3.7
File-specific compression
Different compression algorithms are
better suited to different data, and so one might
like to choose the algorithm to be used for each file. One way to do this in our system would be to place some additional hints
in each inode. The LFS module that
places file data blocks into the element list could use the hints to mark
elements for compression by different algorithms. One possible use of
such a scheme would be to indicate that certain files should not be compressed
at all; this would free those files from the restriction noted in the previous
subsection.
While
file-specific compression could easily be applied to our current software implementation, it would certainly complicate the
hardware design described in Section 5. Moreover, only large files would
benefit from this approach, since only one compression algorithm would be used
for each 16 KBytes of data.
4
Compression algorithms
A wide variety of
compression algorithms could be used for this application, but fast, simple algorithms are clearly preferable.
One suitable algorithm was introduced by
David Wheeler in his red and exp programs [13]; similar
algorithms were also described by Raita and Teuhola [8]. Williams has
developed algorithms that are particularly fast for decompression [15, 16].
The simplest form of
Wheeler’s algorithm (which we will call Algorithm 1) is as follows. A hash table t, whose entries are bytes, is
initialized to a known state, such as all zeroes. For each input byte c, the compressor constructs a hash
value h based on the preceding three bytes. The value found in table entry t[h] is called the predicted character. If
t[h] c, the compressor outputs a token indicating a correct prediction. If t[h] =6 c,
the compressor sets the entry t[h] to be c, and outputs a token indicating that prediction failed
and that the input character was c. If this algorithm expands the
block, the compressor outputs a token indicating that no compression has occurred, followed by a copy of the
original data.
The decompressor
maintains a similar hash table t. For
each token read from the compressor, the
decompressor constructs a hash value h based on the last three bytes written to its output. The
hash function and initial setting of t must be identical in compressor and decompressor.
If the token indicates a successful prediction,
the decompressor
reads and outputs the byte t[h]. If it indicates prediction
failure with the input character c, the decompressor sets the entry t[h] to c and
outputs c.
In
our tests, using Sprite system binaries and an operating system source tree, this algorithm predicts around
50% of the bytes in a typical 16 KByte block and compresses it down to 10 KBytes. We used a modest hash table size (ii 4096 entries) and a
simple hash function (h (256c3 16c2 c1) mod ii, where c is the ith character
preceding the current character c, and is bitwise exclusive-or), and we chose to encode a correct
prediction with one bit and a missed prediction with nine bits.
An
improved version of the algorithm (which we will call Algorithm 2) adds a
second hash table holding an alternative prediction, and a token to indicate a
correct prediction in the second table.
In addition, it applies Huffman coding to the stream of predictions and misses, instead of using a fixed-length code for misses.
Our implementation uses a static Huffman code computed from frequencies
of bytes seen on a typical UNIX disk.
Besides the algorithms based on
Wheeler’s ideas, we tried the LZRW1-A and LZRW3-A algorithms due to Williams. A
full description and implementation are available
elsewhere [15, 16], so we omit the details here.
|
Compressor
|
Compression speed
KBytes/s
|
Decompression Speed
KBytes/s
|
compression
ratio
|
|
Algorithm 1
|
1700
|
2200
|
61%
|
|
Algorithm 2
|
590
|
670
|
51%
|
|
LZRW1-A
|
910
|
2400
|
52%
|
|
LZRW3-A
|
360
|
1500
|
48%
|
|
compress
|
250
|
410
|
50%
|
|
zoo-h
|
45
|
390
|
36%
|
This table shows the performance of six compression algorithms on 240
MBytes of data from a log-structured file system containing Sprite operating
system source and binaries. The figures give the compression speed, decompression
speed, and the ratio of output size to input size (compression ratio).
Compression was performed on 16 KByte blocks.
Compression speed is in kilobytes of uncompressed data processed per second of CPU time, given to two significant
figures. Times were measured on a DECstation 5000/200.
Table 2: Comparison of compression algorithms.
Table 2 illustrates the performance of
these algorithms on data typical for a UNIX
program development environment. For comparison, we include figures for
the popular compress utility,
which uses the LZC algorithm, and the zoo archiver, which uses the LZSS
algorithm. The table shows that the algorithms we chose are quite fast, but better compression could be obtained
by sacrificing speed.
Bell, Witten, and
Cleary give a more thorough comparison of compression algorithms and their
effectiveness on different sorts of data [3]. They also describe the LZC and
LZSS algorithms.
5
LFS and compression hardware
We have arranged our system so that the
compression algorithm can be changed easily.
An obvious improvement would be to replace the compression routine with
a piece of hardware. As noted in the introduction, this would reduce the
performance penalty exacted by software compression, and would increase the
effective disk transfer rate. We have not yet integrated compression hardware
into our prototype, but in this section we discuss how it might best be done.
5.1
System changes
The simplest way to
add hardware compression to our design would be to build a DMA device that reads
uncompressed data from one buffer and writes compressed data to another (and vice versa),
and use it as a direct replacement for our software compression module.
Consider
a disk with a transfer rate of d MBytes per second, and a
compressor that achieves compression
ratio r at a rate of c MBytes per second. Without compression, the time to
transfer ii MBytes is ii /d seconds. With a separate hardware compressor, this becomes ii/c + ii r/d seconds. (Seek and rotational delays are unaffected. We assume
that DMA setup times are negligible for blocks of more than a few kilobytes.) We would like to reduce the total time,
which implies that c > d/ (1 - r). For example, when r 0.5, d 2 MBytes
per second, c must exceed 4 MBytes per second
to improve the speed of disk writes.
A
drawback of this approach is that data traverses the bus three times on its way to disk—once uncompressed,
and twice compressed. Also, compression and decompression
are serialized with disk transfer, not overlapped. These problems suggest that the
compressor should be placed in the disk controller, but doing so requires more
changes to LFS, and quite specialized hardware.
As previously noted,
LFS often needs to place the logical address of one disk block into another disk block that is being written
in the same disk transfer. (For example, it needs to put the locations
of file blocks into inodes.) But it is not
possible to tell whether a
particular disk block will fit in the current segment until compression has taken place, so we cannot determine
what data should be written until the data has been transferred to the
controller for compression.
The
first step to solving this problem is to modify LFS so that each write contains no forward references to
disk blocks. For example, in any particular write,
inode blocks would always follow the file data blocks they point to, and inode
map blocks would follow the inode blocks they point to. Once forward references are eliminated, our problem can be
solved by placing a large buffer in the disk controller to hold the
compressed data. The file system can monitor the status of the buffer as it writes more data, and commit the data to disk
only after compression has taken place.
We can save the cost
of the buffer and overlap the compression with the disk transfer by noticing that, in the absence of forward references, any
prefix of a write is valid. Thus, the file system can prepare a larger amount
of data for writing than will
actually fit in the current segment, and can instruct the controller to
truncate the write if it occupies more than the amount of physical space
available. If a write is truncated,
the file system may have to recalculate the contents of the inode blocks and
inode map blocks before writing them, but none of the blocks that were actually
written need be changed.
To achieve complete
overlap between the compression and the disk transfer, the compressed data stream must be at least as fast as the disk, or the
disk will be starved of data. That
is, cr > d. This could be done by artificially padding the compressed data whenever the data is compressed too
well. In this case, the time to transfer n MBytes of
data becomes m ax (n r/d. n/c). Thus, for a sufficiently fast compressor, the transfer time is improved by the
compression ratio.
Finally, a disk
controller containing a compressor must inform the software where each compressed block fell on the disk.
Ideally, it would also construct the logical block map and append it to the
data being written, in order to avoid an extra disk transfer to place the
map at the end of the segment.
5.2
Compression hardware
Our Algorithms 1 and
2 (described in Section 4 above) can be realized quite easily in hardware at speeds over 10
MBytes per second. The hash function requires one fixed-distance shift and one
exclusive-or per byte. Adequate hash tables can be implemented by RAMs arranged to
provide 16K words of 16 bits each. RAMs with a block erase capability are commercially
available; these allow the tables to be reset to zero in a few cycles at the
start of each block. Both hash table lookups needed for Algorithm 2 can be
implemented with a single memory read, and the
Huffman table lookup can be done
in parallel, so only one memory read and one memory write are required per byte of data processed. In Algorithm 2, a
barrel shifter is needed to pack the variable length codes into bytes.
We
have described this implementation to illustrate that simple, low-cost hardware can provide adequate compression at high speed.
More complex, slower algorithms are already
available in chips running at 10 MBytes per second [1, 4].
6 Performance of prototype
Performance was
measured on a DECstation 5 000/200, an 18 SPECmark machine based on a 25 MHz MIPS R3000 CPU. The disk was an
RZ55, a SCSI disk with a maximum transfer
rate of 1.25 MBytes per second, rotating at 3600 rpm, with
a 1
6ms average seek time. During the timed tests, the disk was never more than 25%
full, so the LFS cleaner did not run.
|
System
|
Time for phase (seconds)
|
Total
|
|
MakeDir
|
Copy
|
ScanDir
|
ReadAll
|
Make
|
|
unmodified LFS
|
1 ± 1
|
4 ± 1
|
4 ± 1
|
4 ± 1
|
58 ± 2
|
71 ± 2
|
|
nocompression
|
0±1
|
5±1
|
4±1
|
4±1
|
64±2
|
78±1
|
|
Algorithm1
|
1±1
|
5±1
|
3±1
|
5±1
|
63±2
|
77±2
|
|
Algorithm 2
|
1 ± 1
|
6 ± 1
|
4 ± 1
|
5 ± 1
|
67 ± 2
|
83 ± 2
|
|
LZRW1-A
|
1±1
|
5±1
|
3±1
|
5±1
|
65±2
|
79±1
|
|
LZRW3-A
|
0±1
|
5±1
|
3±1
|
5±1
|
66±1
|
80±1
|
This table shows the time in seconds
for the Andrew file system benchmark running on six LFS configurations: unmodified LFS, and our modified LFS with
five different compression algorithms. The values given are the mean of three
runs, each on a newly rebooted and otherwise idle DECstation 5000/200
using an RZ55 disk.
Table 3: Running time of Andrew benchmark.
Table 3 shows how
our software compression affects the performance of the system when executing the Andrew file system benchmark [7]. It shows
times for the unmodified LFS system,
and for our modified system using five different compression algorithms. One of
the compression algorithms is the null algorithm, implemented by a
memory-to-memory copy.
The
performance of the modified system with no compression is worse than that of the unmodified system because of two short-cuts
that we took in implementing our prototype.
First, we chose to write the logical block map to disk as a separate I/O
operation, rather than appending
it to the write that was completing the segment. We also introduced an extra copy operation for all data written to
simplify the compressor implementation.
Both of these short-cuts could be eliminated with some additional
effort.
The table shows that Algorithm 2 has the most impact
on performance; it adds 6% to the total time
to execute the benchmark (taking our modified system with no compression as the
basis for comparison). Here, compression is generally asynchronous due to write-behind in the file block
cache. Since only a few megabytes of files are used in the Andrew benchmark,
the files are decompressed only once (in the Copy phase) and reside in
the file system’s buffer cache thereafter.
|
|
Time for test (seconds)
|
|
System
|
Copy file
|
Tree walk
|
|
|
Elapsed
|
CPU
|
Elapsed
|
CPU
|
|
unmodified LFS
|
105 + 1
|
15 + 1
|
2.5 + 0.1
|
0.5 + 0.1
|
|
nocompression
|
128+1
|
17+1
|
4.2+0.1
|
0.7+0.1
|
|
Algorithm1
|
147+1
|
43+2
|
4.2+0.1
|
1.6+0.1
|
|
Algorithm 2
|
206 + 2
|
80 + 4
|
5.8 + 0.2
|
3.1 + 0.1
|
|
LZRW1-A
|
154+2
|
35+4
|
3.9+0.1
|
1.4+0.1
|
|
LZRW3-A
|
191+1
|
48+7
|
4.6+0.1
|
1.9+0.1
|
This table shows elapsed time and
kernel CPU time in seconds for two tests, running on the same six LFS
configurations used in Table 3. In the first test, a 32 MByte file was
copied and flushed to disk—both source and destination were on the file system under test. In the second, find was used to
walk a directory tree of 400 files. The values given are the mean of three runs, each on a newly rebooted and
otherwise idle DECstation 5000/200 using an RZ55 disk.
Table 4: Time for file copy and tree walk.
Table 4 shows the
elapsed time and kernel CPU time for copying a 32 MByte file, and for walking a
directory tree with the UNIX find utility, examining every inode. The effect of compression on performance is
more noticeable, because these tests involve
no user computation. Here, file cache misses cause synchronous compression and decompression operations. The
slowest compression algorithm adds 60% to the time taken to copy a large
file, and about 40% to the time for the tree walk.3
 3The
elapsed time for the tree walk is less for LZRW1-A than for the null
compression algorithm. We are still investigating the cause.
3The
elapsed time for the tree walk is less for LZRW1-A than for the null
compression algorithm. We are still investigating the cause.
As a check on the compression figures of Table 2, we measured the number of physical segments consumed by storing a subtree
of files containing 186 MBytes of operating
system source and binaries. The results agree closely with our
expectations; see Table 5.
|
|
Segments consumed
|
|
System
|
Absolute
|
Relative to
unmodified LFS
|
|
unmodified LFS
|
380
|
100%
|
|
no compression
|
381
|
100%
|
|
Algorithm 1
|
222
|
58%
|
|
Algorithm 2
|
183
|
48%
|
|
LZRW1-A
|
190
|
50%
|
|
LZRW3-A
|
172
|
45%
|
This table shows the number of 512
KByte segments consumed by storing 186 MBytes of operating system source
and binaries, again on the six LFS configurations used in Table 3. The first
column gives the absolute number of segments; the second gives the number
relative to unmodified LFS.
Table 5: Compression obtained on prototype.
Besides
measuring the performance of the system under artificial loads, we also used
the system for simple program development to see whether the performance decrease was perceptible. For
Algorithm 1, the system seemed as responsive as an unmodified system. However, with the slower algorithms we observed
pauses after file system activity. These pauses occurred when the system
flushed large amounts of dirty data to disk,
at which point the compression code was invoked. It appears that Algorithm 1 is
fast enough to make these pauses unobtrusive during normal work, but the other algorithms are not. It
may be possible to eliminate these
pauses by forcing the compression task to yield the processor periodically.
7 Comparison with other work
The Stacker4 system uses a conventional MS-DOS5 file
system format, but intercepts reads and
writes in the device driver and performs compression and decompression on 4 or 8 KByte clusters [14]. A
defragmentation utility can be run
 4Stacker is a trademark of Stac Electronics.
4Stacker is a trademark of Stac Electronics.
5MS-DOS is a registered trademark of Microsoft
Corporation.
periodically to improve the
layout of the files on the disk if updates cause performance to degrade. Stacker demonstrates that on-line
compression can be applied to a conventional
file system with acceptable performance. But as we have shown, compression fits more easily into a log-structured
file system. Moreover, LFS allows us
to pack compressed blocks next to one another without any alignment constraints, which improves the effective
compression ratio. The cleaner automatically
reduces fragmentation, without any additional support. Even meta-data can be
compressed in LFS, without significant impact on the file system code.
The Iceberg6
system also compresses and decompresses as data is read and written, this time in devices that emulate IBM
disk drives [6, 12]. Compression is performed
in hardware, using a variant of the Lempel-Ziv algorithm [17]. Iceberg uses a technique termed dynamic mapping to
avoid problems with layout and fragmentation.
As in LFS, new data does not overwrite old data, and a background task is responsible for collecting free space on
the disk. Unfortunately, details about Iceberg are not publicly
available.
Cate and Gross
advocate a two-level file system, in which files that have not been accessed recently are compressed by a daemon
process [5]. In their ATTIC system,
a compressed file is decompressed when it is first accessed. Subsequent accesses use the decompressed file; the file is
not compressed again until another period of inactivity is detected.
This approach has the advantage that only decompression
is done on-line, and so only the decompression algorithm need be fast;
this allows the use of algorithms that can achieve more compression than those used in our system. (See Table 2, for
example.) In their prototype, a file is compressed or decompressed as a unit,
which may introduce uncomfortable delays when accessing very large files. Our system avoids such delays by
compressing and decompressing in small blocks, yet avoids fragmentation
by exploiting the structure of the log.
One
can view our system as a special case of the general scheme that Cate and Gross describe; our cache of recently accessed files
is the operating system’s file block cache. This thought leads inevitably to
the idea of a hierarchy of caches, with different levels of compression.
Taunton describes a system in
which programs are decompressed automatically by the operating system as they are demand-paged
into memory [10]. Compression is invoked explicitly by the user; each page is compressed separately by
a simple algorithm, and stored in as few
disk blocks as possible. This works well in the system described only because the page size far exceeds the file system
block size, which is not the case in most systems; however, Taunton also
explains
 6Iceberg is a trademark of Storage Technology
Corporation.
6Iceberg is a trademark of Storage Technology
Corporation.
how his scheme can be adapted to more typical systems.
The scheme benefits from concentrating on
executable files, which are read by few things besides the operating
system itself; no attempt is made to make the compression transparent to other
applications.
AutoDoubler7 [11] is a commercial system that
uses a strategy similar to Cate and Gross’s proposal. It uses slow off-line compression and fast
on-line decompression to provide
transparent access to compressed files.
There are many other
products similar in implementation to Stacker and AutoDoubler, using both hardware and software compression. They include
Expanz! Plus8, DoubleDisk9, SuperStor10, and XtraDrive11.
8
Summary
We have demonstrated a factor of two
reduction in disk space consumption by adding on-line compression and
decompression to a log-structured file system used to store system binaries and
an operating system source tree. Even using software
compression, the performance of our system is acceptable on a DECstation
5000/200. The design can be adapted to use hardware compression devices, either
combined with a disk controller or packaged separately. Compression
chips are available that run faster than
most disk transfer rates [1, 4]. Thus, the performance of the file system can actually be improved by
adding specialized hardware, since the effective disk transfer rate can
be increased by as much as the compression factor.
We believe that this
represents a promising technique for combining data compression with the file
system. In addition to their other advantages, log-structured file systems provide an environment in which compression can
be used without the complexities of fragmentation and allocation that
complicate more conventional approaches.
Acknowledgements
Fred Douglis independently developed and pursued the
idea of adding compression to a log-structured
file system, and has provided helpful feedback on this paper.
 7AutoDoubler is a trademark of Salient Software, Inc.
7AutoDoubler is a trademark of Salient Software, Inc.
8Expanz! Plus is a trademark of
InfoChip Systems Inc.
9DoubleDisk
is a trademark of Vertisoft Systems Inc.
10SuperStor
is a trademark of AddStor Inc.
11XtraDrive is a trademark of Integrated Information
Technology Inc.
We would also like to thank Tom Anderson,
Mary Baker, John Ousterhout, Margo Seltzer,
and especially John Hartman. They provided us with a copy of the Sprite
operating system and answered our many questions.
We
received useful comments on early versions of this paper from many people, including Lucille Glassman, Tom
Rodeheffer, Michael Sclafani, Chuck Thacker, and various anonymous referees.
References
[1] AHA32 10 Data Compression
Coprocessor IC Product Brief. Advanced Hardware
Architectures, Inc. P.O. Box 9669 Moscow, Idaho 83843.
[2] M.G. Baker, J.H. Hartman, M.D.
Kupfer, K.W. Shirriff, and J.K. Ousterhout. Measurements of a Distributed File
System. Proceedings of the 13th ACM Symposium on Operating Systems Principles, Asilomar,
13–16 October 1991, pp. 198–212.
[3] T. Bell, I. H. Witten, and J.G.
Cleary. Modeling for Text Compression. ACM Computing
Surveys, Vol. 21, No. 4, December 1989, pp. 557–589.
[4] S. Bunton and G. Borriello. Practical
Dictionary Management for Hardware Data
Compression. Communications of the ACM, Vol. 35, No. 1, January 1992, pp.
95–104.
[5] V. Cate and T. Gross. Combining
the Concepts of Compression and Caching for a Two-Level Filesystem. Proceedings of the 4th International
Conference on
Architectural Support for Programming Languages and Operating Systems (ASPLOS), Santa Clara, California. 8–11 April 1991,
pp. 200–211.
[6] T. Costlow. Compressed Data Makes Iceberg Hot.
Electronic Engineering Times, 3 February 1992, p. 14.
[7] J. Howard et al. Scale and Performance in a
Distributed File System. ACM Transactions on Computer Systems, 6(1), 1988.
[8] T. Raita and J. Teuhola.
Predictive Text Compression by Hashing. Proceedings of the 10th Annual ACM SIGIR
conference on Research and Development in
Information Retrieval. New Orleans, 3–5 June 1987, pp. 223–233.
[9] M. Rosenblum and J.K. Ousterhout. The Design and
Implementation of a Log-Structured File
System, Proceedings of the 13th ACM Symposium on Operating Systems
Principles, Asilomar, 13–16 October 1991, pp. 1–15.
[10] M. Taunton. Compressed
Executables: An Exercise in Thinking Small, Proceedings of the Summer 1991 Usenix Conference, Nashville, 10–14 June,
1991,pp. 385–403.
[11] Salient Software,
Inc. AutoDoubler User Manual. 1992. Salient Software, Inc. 124 University Avenue, Suite 300, Palo Alto,
California 94301.
[12] Storage Technology Corporation.
Iceberg News Release. January, 1992. Storage
Technology Corporation, 2270 South 88th Street Louisville, Colorado 80028-0001.
[13]
D.J. Wheeler. University
of Cambridge Computer Laboratory, Pembroke Street, Cambridge, CB2 3QG, UK.
Private Communication. Wheeler wrote the initial implementations of red and
exp while at Bell Laboratories in November 1983.
[14]
D.L. Whiting and R.A. Monsour. Data Compression Breaks Through To Disk Memory Technology. Computer
Technology Review, Spring 1991. Reprints also
available from Stac Electronics, 5993 Avenida Encinas, Carlsbad, California
92008.
[15] R. Williams. An Extremely Fast
Ziv-Lempel Data Compression Algorithm. IEEE
Data Compression Conference, Snowbird, Utah, 8–11 April 1991.
[16] R. Williams. Data Compression
Directory. Available via anonymous ftp: sirius.itd.adelaide.edu.au:pub/compression
This directory contains descriptions and source code for Williams’ algorithms.
[17] J. Ziv and A. Lempel. A
Universal Algorithm for Sequential Data Compression. IEEE Transactions on Information Theory.
Vol. IT-23, No.3, May 1977, pp. 337–343.
![]()
![]()

![]()
![]()
![]()
![]()
 file block A
file block A
