This document was made by OCR
from a scan of the technical report. It has not been edited or proofread and is
not meant for human consumption, but only for search engines. To see the
scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL
that got you here.
 Specifying
Distributed Systems
Specifying
Distributed Systems
Butler W. Lampson
Cambridge Research Laboratory
Digital Equipment Corporation
One Kendall Square
Cambridge, MA 02139
October 1988
These
notes describe a method for specifying concurrent and distributed systems, and
illustrate it with a number of
examples, mostly of storage systems. The specification method is due to Lam
port (1983, 1988), and the notation is an extension due to Nelson (1987) of
Dijkstra's (1976) guarded
commands.
We
begin by defining states and actions. Then we present the guarded command
notation for composing actions, give an example, and define its semantics in several
ways. Next we explain what
we mean by a specification, and what it means for an implementation to satisfy
a specification. A simple example illustrates these ideas.
The
rest of the notes apply these ideas to specifications and implementations for a
number of interesting
concurrent systems:
Ordinary memory, with two
implementations using caches;
Write
buffered memory, which has a considerably weaker specification chosen to
facilitate concurrent
implementations;
Transactional
memory, which has a weaker specification of a different kind chosen to facilitate fault-tolerant
implementations;
Distributed memory, which
has a yet weaker specification than buffered memory chosen to facilitate highly
available implementations. We give a brief account of how to use this memory
with a tree-structured address space in a highly available naming service.
Thread synchronization
primitives.
States and actions
We describe a system as a state space, an initial point
in the space, and a set of atomic actions which take a state into an outcome,
either another state or the looping
outcome, which we denote 1. The state space is the cartesian product of
subspaces called the variables or state functions,
NATO ASI Series, Vol. F 55
Constructise Methods in Computing Sciutiu, Edited by M. Broy
SpringurNerlag Berlin ficidc11),re 1989
 depending
on whether we are thinking about a program or a specification. Some of the
variables and
actions are part of the system's interface.
depending
on whether we are thinking about a program or a specification. Some of the
variables and
actions are part of the system's interface.
Each
action may be more or less arbitrarily classified as part of a process. The
behavior of the system is determined by the rule that from state s the
next state can be s'
if there is any action that takes
s to
s'. Thus
the computation is an arbitrary interleaving of actions from different processes.
Sometimes
it is convenient to recognize the program counter of a process as part of the
state. We will
use the state functions:
at(a) true
when the PC is at the start of operation a
in(a) true
when the PC is at the start of any action in the operation a
after(a) true when the PC is immediately after
some action in the operation a, but not in(a).
When
the actions correspond to the statements of a program, these state components
are essential, since the ways in which they can change reflect the
flow of control between statements. The soda machine example below may help to clarify
this point.
An
atomic action can be viewed in several equivalent ways.
· A
transition of
the system from one state to another; any execution sequence can be described by an interleaving
of these transitions.
Define the guard of A by
G(A)
= wp(A, false) or G(A)s = (3 0; A so)
G(A)
is true in a state if A relates it to some outcome (which might be 1). If A is
total, 7(A) = true.
We
build up actions out of a few primitives, as well as an arbitrarily rich set of
operators and datatypes which we won't describe in detail. The primitives are
sequential
composition
-3 guard
or
else
variable
introduction
if ... fi
do ... od
These are defined
below in several equivalent ways: operationally, as relations between states, and
as predicate transformers. We omit the relational and predicate-transformer
definitions of du For
details see Dijkstra (1976) or Nelson (1987); the latter shows how to define do
in terms of the
other operators and recursion.
The
precedence of operators is the same as their order in the list above; i.e.,
";" binds most tightly and "I" least tightly.
Actions: operational definition (what the machine does)
· 

 A relation between states and outcomes, i.e.,
a set of pairs; state, outcome. We usually define the relation by
A relation between states and outcomes, i.e.,
a set of pairs; state, outcome. We usually define the relation by
A so = P(s, o)
If
A contains (s, o)
and (s, o', o # o', A is non-deterministic. If
there is an s for
which A contains
no (s, o), A is partial.
· A
relation on
predicates, written (P) A (Q) If
A s s' then
P(s) Q(s')
· A
pair of predicate
transformers: wp and wlp, such that wp(A, R) = wp(A, true)
A wlp(A, R)
wlp(A, ?)
distributes over any conjunction
wp (A,
?) distributes over any non-empty conjunction
The connection between A as a relation and A as a
predicate transformer is wp(A, R) s = every outcome of A
from s satisfies R
wlp(A, R) s = every proper outcome of A
from s satisfies
R We
abbreviate this with the single line
w(l)p(A, R) s = every (proper) outcome of A
from s satisfies
R Of course, the looping outcome doesn't satisfy any
predicate..

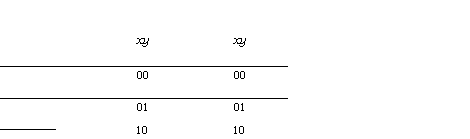
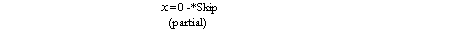


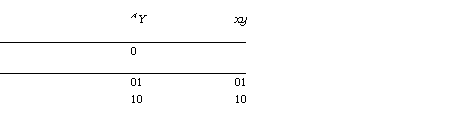
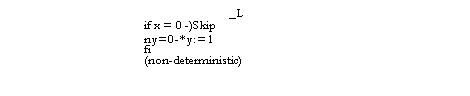

 Actions: relational definition
Actions: relational definition
skip SO E S
= 0
loop SO =0=1
fail so false
(P-- A) so EPSA ASO
(A q B) SO E A so v
B so
(A M B) so -= A so v (B so A -1G(A) S)
(A ; B) SO a (3
s': A ss' A B
s'o) v (A so A 0 = _L )
(if A fi) so E- A so v (—G(A) s A o
= 1)
(x := y) so o is the same state as s, except
that the x component equals y.
(x I A) so =- (V s', projx(s)=s A
projx(op=o
A s'o' ), where projx is the projection that drops the x component of the
state, and takes 1 to itself. Thus I
is the operator for variable introduction.
See figure 1 for an example which shows the
relations for various actions. Note that if A fi makes the relation
defined by A total by relating states such that G(A)=false to 1.
The idiom x I P(x) -4 A can be read
"With a new x such that P(x) do A". Actions: predicate
transformer definition
 w(l)p(skip, R)
w(1)p(loop, R) w(l)p(fail, R) w(l)p(P-->
A, R) w(l)p(A q B, R) w(l)p(A M B, R) w(l)p(A ; B, R) w(l)p(x := y, R) w(l)p(x I A, R)
wp(if A fi, R) wlp(if A fi, R)
w(l)p(skip, R)
w(1)p(loop, R) w(l)p(fail, R) w(l)p(P-->
A, R) w(l)p(A q B, R) w(l)p(A M B, R) w(l)p(A ; B, R) w(l)p(x := y, R) w(l)p(x I A, R)
wp(if A fi, R) wlp(if A fi, R)
R
false(true)
true
P v w(l)p(A, R) w(l)p(A, R) A w(l)p(B, R)
w(l)p(A,
R) A (G(A) v w(Dp(B, R)) w(l)p(A, w(l)p(B,
R))
R(x: y)
V x: w(l)p(A, R) wp(A,
R) A G(A)
wlp(A,
R)
G(.-)
=
true
true false
P A G(A)
G(A) v
G(B) C(A) v G(B) ,wp(A, ,G(B)) true
3 x: G(A)
true
true
|
|
|
y : (25, 50);
|
|
|
|
|
|
|
Abstraction function
|
F
|
|
a:
|
do
|
(x:= )
|
if at(a)
|
I
|
|
13:
|
|
do(x<50 )—>
|
0 at((3)—>
|
if
x=0
—>
|
|
|
|
|
|
q
x=25-4
|
|
|
|
|
|
q
x=50—>
|
|
|
|
( y := depositCoin
|
q
at(y)--4
|
if x=0 -4
|
|
|
|
; x+y 5 50 —> skip )
|
|
q
x=25—>
|
|
|
|
|
|
qx=50—>
fi
|
|
8:
|
|
; ( x := x+y
|
q
at(8)—>
|
if x+y=25-*
|
|
|
|
|
|
q
x+y=50—>
|
|
|
|
od
|
|
q x+y=75--) fi
|
|
E:
|
od
|
( dispenseSoda )
|
q at(E)—>
fi
|
|
Notation
In writing the specifications and implementations, we
use a few fairly standard notations. If T is a type, we write t, t', ti
etc. for variables of type T.
If el, c,
are constants, (el__ cn) is the enumeration
type whose values are the ci.
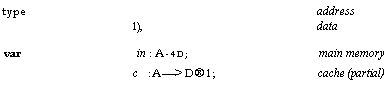

![Text Box: rnsimptc[a] : d = if c[a] —> d := c [a]
d := m[a]
fi](40-SpecDistSysOCR_files/image018.gif)

![Text Box: dirty(a): BOOL c[a] 1A c[a] m[a]
FlushOne a I c[a] 1—) do dirty[a] m[a] := c[a] od; dal :=1
Load(a) = ( do c[a] =1 FlushOne; c[a] := m[a] od )
Read(a, var d ) = Load(a); ( d := c[a])
Write(a, d) ( if c[a] = 1 —> FlushOne 21 skip fi ) ; ( c[a] d)
Swap (a, d, var d' ) = Load(a); ( d' c[a]; dal := d)](40-SpecDistSysOCR_files/image020.gif)

 If
T and U are types, T ED U is the disjoint union of T and U. If c is
a constant, we write T 0 c •for T ED {c).
If
T and U are types, T ED U is the disjoint union of T and U. If c is
a constant, we write T 0 c •for T ED {c).
If T and U are
types, T —> U is the type of functions from T to U; the overloading with the of
guarded commands is hard to avoid. Iff is a function, we
write f(x) or
f [x] for
an application of f,
and f := y
for the operation that changes f [x] to
y and
leaves f the same
elsewhere. If f is
undefined
at x, we write f jxj = 1.
If
T is a type, sequence of T is the type of all sequences of elements of T,
including the empty sequence. T is a subtype of sequence of T. We write s II s' for
the concatenation of two sequences, and A for the empty sequence.
( A ) is an atomic action with the same semantics as A in
isolation. Memory
Simple memory
Here is
a specification for simple addressable memory.
type A; address
Et; data
var m : A
-4 D; memory
Read(a, var d ) = ( d := Ma])
Write(a, d) =
(m[a] := d)
Swap(a, d, var
d'
) = ( d' := m[a];
m[a] d)
Cache memory
We write
cp instead of c[p] for readability.
Now we look at an
implementation that uses a write-back cache. The abstraction function is given
after the variable declarations. This implementation maintains the invariant
that the number of addresses at which c is
defined is constant; for a hardware cache the motivation should be obvious.
A real cache would maintain a more complicated invariant, perhaps bounding the number of addresses
at which c is defined.

![Text Box: type A; address
D; data
P; processor
var rn: A —>D; main memory
c : P—>A—>D 1; caches (partial)
abstraction function
nisimple[a] : d = if 3 p: cp[a] 1—a d:= cp[a]
d:= m[a]
fi](40-SpecDistSysOCR_files/image025.gif)
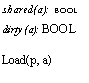
![Text Box: = 3 p, q: cp[a] 1 n cq[a]](40-SpecDistSysOCR_files/image027.gif)
![Text Box: • do cp[a] = 1—> FlushOne(p)
; if ( q I cq[a] 1 —>
fi](40-SpecDistSysOCR_files/image028.gif)
![Text Box: cp[a] := cq[a]) (cp[a] := m[a] )](40-SpecDistSysOCR_files/image029.gif)
![Text Box: = 3p: cp[a] in cp[a] m[a]](40-SpecDistSysOCR_files/image030.gif)

 Write-buffered
memory
Write-buffered
memory
We
now turn to a memory with a different specification. This is not another implementation of the simple memory specification. In
this memory, each processor sees its own writes as it would in a simple memory, but it sees only a
non-deterministic sampling of the writes done by other processors. A FlushAll operation is added to permit
synchronization.
The motivation for using
the weaker specification is the possibility of building a faster processor if writes don't have to be synchronized as
closely as is required by the simple memory specification. After giving the specification, we show how
to implement a critical section within which variables shared with other
processor can be read and written with the same results that the simple memory
would give.
|
type
var
|
A;
P;
In:
A -3D;
b P -4 A —> D I :3) 1;
|
address
data
processor
main memory beers (partial)
|
Flush(p,
a) = bp[a] 1 m[a]
:= bpial); ( b p[a] := 1)
FlushSome = p, a I Flush(p, a); FlushSome
 = a I cp[a] -->
= a I cp[a] -->
![Text Box: Read(p, a, var d ) if ( bp[a] = 1—> d := m [a] )
q (q1bq[a] 1-3 d := a] ) fi
Write(p, a, d) • (bp[a] := d)
Swap (p, a, d, var d' ) = FlushSome; ( d' := midi; m[a] := d)
• do a I Flush(p, a) od
Critical section](40-SpecDistSysOCR_files/image034.gif) ( do —shared[a] A dirty[a]
—> m[a] := cp[a] od
) ; cp[a] _L
( do —shared[a] A dirty[a]
—> m[a] := cp[a] od
) ; cp[a] _L
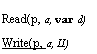 = Load(p, a); (d := cp[a])
= Load(p, a); (d := cp[a])
if cp[a] = FlushOne(p) skip fi
( cp[a] := d
; do q I cq[a]# 1 n eq[a] cp[a]-3 cq[a] := cp[a] od


 do d I
do d I
(dp:=1)
do(dp 0) -, Swap(p, I, 1,
dp)
od
critical
section FlushAll(p)
Write(p, I, 0) non-critical
section od
initially
V p,
a : bp[a] = 1, m[l] = 0
assume
A e I I A independent of m : no Read, Write or Swap in A
A e
18p1 A
independent of m[1]: no Read, Write or Swap(p, I, ...) in
A
The proof depends on the following invariants for the
implementation. Invariants
(1)
CSp (,CSqvp=q)
A M [1]
A bqin *0
where CSp
= in(Seicp) v ( at(pp) A dp = 0 )
(2)
in(8ep) A a I bp[o]
= 1
 Transactions
Transactions
This
example describes the characteristics of a memory that provides transactions so
that several writes can be done atomically with respect to
failure and restart of the memory. The idea is that the
memory is not obliged to remember the writes of a transaction until it has
accepted the transaction's commit; until then it may discard the writes and
indicate that the transaction has aborted.
A
real transaction system also provides atomicity with respect to concurrent
accesses by other transactions, but this elaboration is beyond the scope of these
notes.
We write
Proci(...) for Proc(t, ...) and It for l[t].
msimple = m
Abort1() = ( do a 111[a]
# h m[a] := lt[a]; le[a] :=1 od ) ; x abort
Beein,0 =
do a I lt[a]
# 1-> ( lt[a] := )
od
Read1(a, var d, var
x) = ( d :=
m[a] ); x := ok
Abort
Writet(a, d, var x) = do
i[a] =1 ->
(lt[a]
:= m[a]) od; ( m[a]:=c1); x := ok
Abort
 : A -4D; memory
: A -4D; memory
b :T > A - >ID; backup
( m := bt) ;
x := abort
=
(bt:=m)
( d
:= m[a]) ; x := ok Abort
( m[a]:=d) ;
x := ok
Abort
=
x ok q Abort
This is one of the
standard implementations of the specification above: the old memory values are remembered, and
restored in case of an abort.
var m : A
.-D; memory
I : T ) -4D E I 3 I 1; log
abstraction
function
Ma]:
d =
if //[a] 1 -> d:= [a]
d := m[a]
fi
Redo implementation
This is the other standard implementation: the writes are
remembered and done in the memory only at commit time.
Essentially the same work is done as in the undo version, but in different places; notice how
similar the code sequences are.
var m : A
-> D; memory
1 : T ) A - ED 1; log
abstraction
function
b m
msimple[a]: d if
t I /,[a]1-4 d := [a]
d := m[a]
fi
Abort = x := abort
Begin(0 = do a I h[a] (h[a] := 1
) od
Readr(a, var d , var x) = if /gal * 1 d := It[a] s(d = m [a] ) fi;
x := ok
Abort
Writet(a d, var x) = lt[a] := d ; x := ok
Abort
Commit1(var
x): (
do
a I lt[a] *1-> m[a] := h[a];
lt[a] :=1 od ) ; x :=
ok
D Abort


![Text Box: abstraction function bt[a]: d
msimple[a]: d
Abort,()
ftgirit()](40-SpecDistSysOCR_files/image060.gif)
![Text Box: = if li[a] * --+ d := It [a]
d := m[a]
fi
= if t I abt lt[a]*1-- d:=1Jal
d := m[a]
fi
(abt := true)
do a I ( h[a] * 1) ( m[a] := It[a] ; ( I t[a] := 1) od
x := abort
= abt:= false; do a I lt[a] *1 —3( lt[a] := I) od](40-SpecDistSysOCR_files/image061.gif)
![Text Box: Read (a, var d, var x) = —Iabt (d := m[a]); x := ok
0 Abort
Writet(a, d, var x) = —Iabt do h[a] = —+ (It[a] := m[a] ) od; ( m[a]:=d ); x := ok
0 Abort
Committ(var x) = —tabt —) x := ok
Abort
Name service
This section describes a tree-structured storage system which was designed as the basis of a large-scale, highly-available distributed name service. After explaining the properties of the ser¬vice informally, we give specifications of the essential abstractions that underlie it.
A name service maps a name for an entity (an individual, organization or service) into a set of la¬beled properties, each of which is a string. Typical properties are
password=XQE$# mailboxes={Cabernet, Zinfandel)](40-SpecDistSysOCR_files/image062.gif)
 network
address=173#4456#1655476653 distribution
list={Birrell, Needham, Schroeder}
network
address=173#4456#1655476653 distribution
list={Birrell, Needham, Schroeder}
A name service is not a general database: the set of
names changes slowly, and the properties given name also change
slowly. Furthermore, the integrity constraints of a useful name servit. are
much weaker those of a database. Nor is it like a file directory system, which
must create look up names much faster than a name service, but need
not be as large or as available. Eithu database or a file system root can be named by
the name service, however.
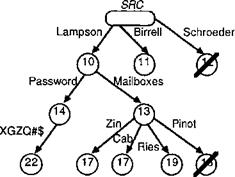
Figure
2: The tree of directory values
A directory is not simply a mapping from simple names to
values. Instead, it contains a tree oi values (see Figure
2). An arc of the tree carries a name (N), which is just a string,
written nex the arc in the figure. A node carries a timestamp (S),
represented by a number in the figure, al mark which
is either present or absent. Absent nodes are struck through in
the figure. A path through the tree is defined by a sequence of
names (A); we write this sequence in the Unix
e.g.,
Lampson/Password. For the value of the path there are three interesting cases:
· If
the path al n ends in a leaf that is an only child, we say that n is
the value of a. This rule applies to the path
Lampson/Password/XGZQ#$3, and hence we say that XGZQ#$3 is value
of Lampson/Password.
· If
the path a/ni ends in a leaf that is not an only child, and its siblings
are labeled ni...nk, we say that the set [ni...nk)
is the value of a. For example, {Zin, Cab, Ries, Pinot} is the val of
Lampson/Mailboxes.
· If
the path a does not end in a leaf, we say that the subtree rooted in the
node where it ends i the value of a. For example, the value of Lampson
is the subtree rooted in the node with timestamp 10.
An
update to a directory makes the node at the end of a given path present or
absent. The upda is timestamped, and a later timestamp takes precedence over an
earlier one with the same path.











 The
subtleties of this scheme are discussed later, its purpose is to allow the tree
to be updated concurrently from a number of places without any prior
synchronization.
The
subtleties of this scheme are discussed later, its purpose is to allow the tree
to be updated concurrently from a number of places without any prior
synchronization.
A
value is determined by the sequence of update operations which have been
applied to an initial empty value. An update can be thought of as a
function that takes one value into another. Suppose the update functions have the
following properties:
· Total: it always
makes sense to apply an update function.
· Commutative:
the order in which two updates are applied does not affect the result.
· Idempotent:
applying the same update twice has the same effect as applying it once.
Then
it follows that the set of
updates that have been applied uniquely defines the state of the value.
It can be shown that the
updates on values defined earlier are total, commutative and idempotent. Hence
a set of updates uniquely defines a value. This observation is the basis of the
concurrency control scheme for the name service. The right side of
Figure 3 gives one sequence of updates which will produce the value on the left.
|
P Lampson:4/Password:11/U1086Z:12
P Lampson:10
P Birre11:11
A Schroeder:12
P Lampson:10/Mailboxes:13 P Lampson:l 0/Password:l 4
P Lampson:10/Mailboxes:13/Zin:17 P Lampson:10/Mailboxes:13/Cab:17
A Lampson:10/Mailboxes:13/Pinot:18
P Lampson:l 0/Mailboxes:13/Ries :19
P
Lampson:10/Password:14/XGZQ#$:22
|
Figure 3: A possible sequence of updates
The
presence of the timestamps at each name in the path ensures that the update is
modifying the value that the client intended. This is
significant when two clients concurrently try to create the same
name. The two updates will have different timestamps, and the earlier one will
lose. The fact that later modifications, e.g. to set the password,
include the creation timestamp ensures that those made by the
earlier client will also lose. Without the timestamps there would be no way to tell them apart, and
the final value might be a mixture of the two sets of updates.
The
client sees a single name service, and is not concerned with the actual
machines on which it is implemented or the replication of the
database which makes it reliable. The administrator allocates
resources to the implementation of the service and reconfigures it to deal with
long-term failures. Instead of a single directory, he sees a set of
directory copies (DC)
stored in different


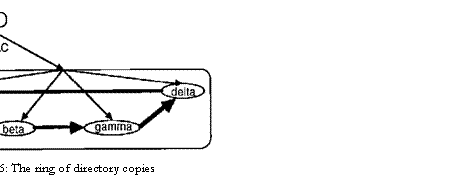
servers. Figure 4 shows this situation for the DEC/SRC
directory, which is stored on four servers named alpha, beta,
gamma, and delta. A directory reference now includes a list of the
servers that store its DCs. A lookup can try one or more of the servers to find
a copy from which
to read.
The copies are kept approximately, but not exactly the
same. The figure shows four updates to SRC, with
timestamps 10, 11, 12 and 14. The copy on delta is current to time 12, as
indicate by the italic 12 under it, called its lastSweep field. The others
have different sets of updates, bti are current only to time
10. Each copy also has a nextS value
which is the next timestamp it wil assign to an update originating there; this
value can only increase.
An update originates at one DC, and is initially
recorded there. The basic method for spreading updates to all the copies is a sweep operation, which visits
every DC, collects a complete set 01 updates, and then writes
this set to every DC. The sweep has a timestamp sweepS, and before reads
from a DC it increases that DC's nextS
to sweepS;
this ensures that the sweep collects all updates
earlier than sweepS. After
writing to a DC, the sweep sets that DC's lastSweep to
sweepS.
Figure 5
shows the state of SRC after a sweep at time 14.
14 14 14 14
Lampson 10 Lampson
10 Lampson 10 Lampson 10 Needham 11 Needham
11 Needham 11 Needham 11 Birrell 12
Birrell 12 Birrell 12 Birrell 12 Schroeder 14 Schroeder14 Schroeder 14
Schroeder 14

Figure
5: The directory after a Sweep
 In
order to speed up the spreading of updates, any DC may send some updates to any
other DC • in a message. Figure 4 shows the updates for Birrell
and Needham being sent to server beta. Most updates should be
distributed in messages, but it is extremely difficult to make this method fully reliable. The
sweep, on the other hand, is quite easy to implement reliably.
In
order to speed up the spreading of updates, any DC may send some updates to any
other DC • in a message. Figure 4 shows the updates for Birrell
and Needham being sent to server beta. Most updates should be
distributed in messages, but it is extremely difficult to make this method fully reliable. The
sweep, on the other hand, is quite easy to implement reliably.
A
sweep's major problem is to obtain the set of DCs reliably. The set of servers
stored in the parent is not suitable, because it is too
difficult to ensure that the sweep gets a complete set if the directory's
parent or the set of DCs is changing during the sweep. Instead, all the DCs are
linked into a ring, shown by the fat arrows in
figure 6. Each arrow represents the name of the server to which
it points. The sweep starts at any DC and follows the arrows; if it eventually
reaches the starting point, then it has found a complete set of DCs.
Of course, this operation need not be done sequentially; given a
hint about the contents of the set, say from the parent, the sweep can visit all the DCs
and read out the ring pointers concurrently.
Distributed writes
Here
is the abstraction for the name service's update semantics. The details of the
tree of values are deferred until later, this specification depends
only on the fact that updates are total, commutative and idempotent.
We begin with a specification that says nothing about multiple copies; this is the
client's view of the name service. Compare this with the write-buffered memory.
type V; value
U = V—) V; update, asstuned total,
commutative, and idempotent
W = set of U; updates "in
progress"
 var
var
AddSome(var v)
Read(var v) Update(u) Sweep()
m: V; memory
b :
W; buffer
= UlUE bA 14(V) V -* V := U(1); AddSome(v)
skip
= ( v := m ; AddSome(v) )
=
b := b u (u))
= (douluE b—m:=u(m);b:=b—{u}od)
DCs
can be added or removed by straightforward splicing of the ring. If a server
fails permanently, however (say it gets blown up), or if the set of servers is
partitioned by a network failure that lasts for a long time, the ring
must be reformed. In the process, an update will be lost if
it originated in a server that is not in the new ring and has not been
distributed. The ring is reformed by starting a new epoch for
the directory and building a new ring from scratch, using the
DR or information provided by the administrator about which servers should be
included. An epoch is identified by a timestamp, and the most recent epoch that
has ever had a complete ring is the one that defines the
contents of the directory. Once the new epoch's ring has been successfully
completed, the ring pointers for older epochs can be removed. Since starting a
new epoch may change the database, it is never done
automatically, but must be controlled by an administrator.
Update and Sweep
were called Write and Flush in the specification for buffered writes. This differs
in that there is no ordering on b, there are no updates in b that
a Read is guaranteed to see, and there is no Swap operation.
You
might think that Sweep is too atomic, and that it should be written to move one
u from
b to In in
each atomic action. However, if two systems have the same b u In, the
one with the smaller b is an implementation of the one with the larger
b, so
a system with non-atomic Sweep implements a specification with atomic Sweep.
We
can substitute distinguishable for idempotent and ordered for commutative as
properties of updates. AddSome and Sweep must be changed to
apply the updates in order. If the updates are ordered, and we
require that Update's argument follows any update already in in, then
the boundary between m and b can
be defined by the last update in tn. This is a conveneint way to summarize
the information in b
about how much of the state can be read
deterministically. In the name server application the updates are ordered
by their timestamps, and the boundary is called last Sweep.
 N-copy version
N-copy version
Now for an implementation that makes the copies visible.
It would be neater to give each copy its own version of m and its own set b of
recent updates. However, this makes it quite difficult to
define the abstraction function. Instead, we simply give each copy its version
of b, and
define m to
be the result of starting with an initial value vo and applying all the updates
known to every copy. To this end the auxiliary function apply turns a set of
updates w into
a value v by
applying all
of them to vo.
type V; value
U = 11-4 V; update, assumed total,
commutative, and idempotent
W = set of U; updates "in progress"
P; processor
var b :P- W; buffers
Abstraction function
msimple = apply( n b[ p])
peP

![Text Box: = V b[ p]- n b[ p]
pet' peP](40-SpecDistSysOCR_files/image092.gif)
 In
other words, the abstract m is all the updates that every processor has, and
the abstract b is
all the
updates known to some processor but not to all of them.
In
other words, the abstract m is all the updates that every processor has, and
the abstract b is
all the
updates known to some processor but not to all of them.
Tree memory
Finally,
we show the abstraction for the tree-structured memory that the name service
needs. To be used with the distributed writes specification, the
updates must be timestamped so that they can be ordered. This detail
is omitted here in order to focus attention on the basic idea.
We use the notation:x y for x # y x := y. This
allows us to copy a tree from v' to v with
the
idiom
do a I v[a] via] od
which
changes the function v to agree with v' at every point. Recall also
that II stands for concatenation of sequences; we use sequences of
names as addresses here, and often need to concatenate such path names.
type N; name
data
A = sequence of N; address
V=A->DEDI; tree value
var m : V; memory
Read(a var v ) =
( do a' I v[a] m[a II
a] od )
Write(a, v) = ( do a' I ml-a II a] 4-- vf od )
Write(a, d) = v I V a: v[a] =1 v[A] = d ; Write(a, v)
apply(w): v Read(p, var v) Update(p,
u)
Sweep()
=
v
:= vo; do ulue w -> v':= u(v);w := w - (o)od
![Text Box: Read copies the subtree of m rooted at a to v. Write(a, v) makes the subtree of m rooted at a equal to v. Write(a, d) sets m[a] to d and makes undefined the rest of the subtree rooted at m.](40-SpecDistSysOCR_files/image094.gif) = v := apply(b[p])
= v := apply(b[p])
= (
b[p] := b[p] v (u) )
=
w I (w := lJ b[ )
peP
; do p,u W A Lift b[p]-> ( b[p]
:= b[p] Li (a)) od
Since
this meant to be viewed as an implementation, we have given the least atomic
Sweep, rather than the most atomic one. Abstractly an update
moves from b to
m when
it is added to the last processor that didn't have it already.







 Timestanzped tree memory
Timestanzped tree memory
We
now introduce timestamps on the writes, in fact more of them that are needed to
provide write ordering. The name service uses timestamps at each
node in the tree to provide a poor man's transactions: each point in the memory
is identified not only by the a that leads to it, but also by the timestamps of
the writes that created the path to a. Thus conflicting use of the
same names can be detected; the use with later timestamps will
win. Figure 3 above shows an example.
We show only the write of a single value at a node
identified by a given timestamped address b. The write fails (returning
false in x) unless the timestamps of all the nodes on the path to node b match the ones in b. We write m[a].d and m[a].s for the d
and
s components of m[a].
type N; name
data
S; timestamp
A = sequence of N; address
V = A —3 (D x S) 1; tree value
B = sequence of (N x S); address with timestamps
var in : V; memory
Read(a, var v ) = ( do a' I v[a] 4— m[a II od )
Write(b, d, var x) ( a I
for all iength(b): al[i] = b[t].n —4
if for all
0<i<length(b), m[a[1..i]].s = b[1].s —9 do
a' I m[a II <— l od
m[a] := (d, b[length(b)].․)
x := true
x := false
fi
The
ordering relation on writes needed by the distributed writes specification is
determined by the timestamped address:
b1<b2= 3 i<length(b1):
j<i bifil=1)2[1] A bifiln=b2fil.n
A bi[1].s<b2rits
In
other words, bi<b2 if they match exactly up to some
point, they have the same name at that point, and b1 has
the smaller timestamp at that point. This rule ensures that a write to a node
near the root takes precedence over later writes into the subtree rooted at that node
with an earlier timestamp. For example, Lampson:10 takes
precedence over Lampson:4/Password:l 1.
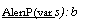

 =
( s= free
— s := busy; b := false
=
( s= free
— s := busy; b := false
q
self E a —) a := a -- ( self); b := true
A. Birrell
et. al. (1987). Synchronization primitives for a multiprocessor: A formal
specification ACM Operating Systems Review 21(5): 94-102.






![Text Box: For comparison, we give the original Larch version of Wait: type Condition = set of Thread initially [ }
procedure Wait(var m: Mutex; var c: Condition) = composition of Enqueue, Resume end requires m = self
modifies at most [ m, c ]
atomic action Enqueue
ensures (cpost=insert(c, self)) A (mpost = nil)
atomic action Resume
when (m = nil) A --,(self E c)
ensures mpost = self & unchanged [ c ]](40-SpecDistSysOCR_files/image111.gif) E. Dijkstra (1976). A Discipline of Programming. Prentice-Hall.
E. Dijkstra (1976). A Discipline of Programming. Prentice-Hall.
L.
Lamport (1988). A simple approach to specifying concurrent systems. Technical
report 15 (revised), DEC Systems Research Center, Palo Alto. To
appear in Comm. ACM, 1988.
L.
Lamport (1983). Specifying concurrent program modules. ACM Transactions on Programming Languages
and Systems, 5(2):
190-222.
L.
Lamport and F. Schneider (1984). The "Hoare logic" of CSP, and all
that. ACM Transaction.
on Programming Languages and Systems, 6(2): 281-296.
B. Lampson
(1986). Designing a global name service. Proc. 4th ACM Symposium on Principles of Distributed
Computing, Minaki,
Ontario, pp 1-10.
G.
Nelson (1987). A generalization of Dijkstra's calculus. Technical report 16,
DEC Systems Research
Center, Palo Alto.
![]() Specifying
Distributed Systems
Specifying
Distributed Systems






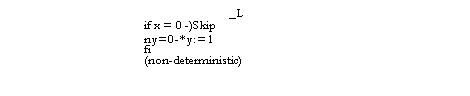

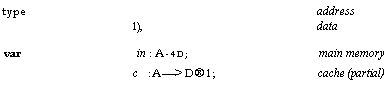
![Text Box: rnsimptc[a] : d = if c[a] —> d := c [a]
d := m[a]
fi](40-SpecDistSysOCR_files/image018.gif)
![Text Box: dirty(a): BOOL c[a] 1A c[a] m[a]
FlushOne a I c[a] 1—) do dirty[a] m[a] := c[a] od; dal :=1
Load(a) = ( do c[a] =1 FlushOne; c[a] := m[a] od )
Read(a, var d ) = Load(a); ( d := c[a])
Write(a, d) ( if c[a] = 1 —> FlushOne 21 skip fi ) ; ( c[a] d)
Swap (a, d, var d' ) = Load(a); ( d' c[a]; dal := d)](40-SpecDistSysOCR_files/image020.gif)


![Text Box: type A; address
D; data
P; processor
var rn: A —>D; main memory
c : P—>A—>D 1; caches (partial)
abstraction function
nisimple[a] : d = if 3 p: cp[a] 1—a d:= cp[a]
d:= m[a]
fi](40-SpecDistSysOCR_files/image025.gif)
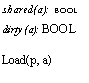
![Text Box: • do cp[a] = 1—> FlushOne(p)
; if ( q I cq[a] 1 —>
fi](40-SpecDistSysOCR_files/image028.gif)
![Text Box: cp[a] := cq[a]) (cp[a] := m[a] )](40-SpecDistSysOCR_files/image029.gif)
![Text Box: Read(p, a, var d ) if ( bp[a] = 1—> d := m [a] )
q (q1bq[a] 1-3 d := a] ) fi
Write(p, a, d) • (bp[a] := d)
Swap (p, a, d, var d' ) = FlushSome; ( d' := midi; m[a] := d)
• do a I Flush(p, a) od
Critical section](40-SpecDistSysOCR_files/image034.gif)
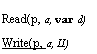


![Text Box: var m : A -4D;
a b: P-*A--,D Gal;
const I := the address of a location to be used as a lock
abstraction function
ntsimpte[a] d = if p I bp[a] 1-3 d := p[a]
d := m[a]
fi](40-SpecDistSysOCR_files/image041.gif)

![Text Box: = d,e I bp[a] = (Ill e (m[a):= d);(bp[a]:= e)
= p, a I Flush(p, a); FlushSome
q skip
= if ( bp[a] = A d := In[o])
q ( q, el, d', e2 I bg[a] = el II d' II e2](40-SpecDistSysOCR_files/image045.gif)
![Text Box: fi
( b p[a] := b p[a] II d)](40-SpecDistSysOCR_files/image047.gif)



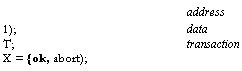




![Text Box: abstraction function bt[a]: d
msimple[a]: d
Abort,()
ftgirit()](40-SpecDistSysOCR_files/image060.gif)
![Text Box: = if li[a] * --+ d := It [a]
d := m[a]
fi
= if t I abt lt[a]*1-- d:=1Jal
d := m[a]
fi
(abt := true)
do a I ( h[a] * 1) ( m[a] := It[a] ; ( I t[a] := 1) od
x := abort
= abt:= false; do a I lt[a] *1 —3( lt[a] := I) od](40-SpecDistSysOCR_files/image061.gif)
![Text Box: Read (a, var d, var x) = —Iabt (d := m[a]); x := ok
0 Abort
Writet(a, d, var x) = —Iabt do h[a] = —+ (It[a] := m[a] ) od; ( m[a]:=d ); x := ok
0 Abort
Committ(var x) = —tabt —) x := ok
Abort
Name service
This section describes a tree-structured storage system which was designed as the basis of a large-scale, highly-available distributed name service. After explaining the properties of the ser¬vice informally, we give specifications of the essential abstractions that underlie it.
A name service maps a name for an entity (an individual, organization or service) into a set of la¬beled properties, each of which is a string. Typical properties are
password=XQE$# mailboxes={Cabernet, Zinfandel)](40-SpecDistSysOCR_files/image062.gif)


















![Text Box: For comparison, we give the original Larch version of Wait: type Condition = set of Thread initially [ }
procedure Wait(var m: Mutex; var c: Condition) = composition of Enqueue, Resume end requires m = self
modifies at most [ m, c ]
atomic action Enqueue
ensures (cpost=insert(c, self)) A (mpost = nil)
atomic action Resume
when (m = nil) A --,(self E c)
ensures mpost = self & unchanged [ c ]](40-SpecDistSysOCR_files/image111.gif)