This document was made by
OCR from a scan of the technical report. It has not been edited or proofread
and is not meant for human consumption, but only for search engines. To see the
scanned original, replace OCR.htm with Abstract.htm or Abstract.html in the URL
that got you here.
Mesa Language Manual
by James
G. Mitchell William
Maybury Richard Sweet
Version
5.0 April 1979
CSL-79.3
The Mesa language is one component of a
programming system intended for developing and maintaining a
wide range of systems and applications programs. Mesa supports the development
of systems composed of separate modules with controlled sharing of information among
them. The language includes facilities for user-defined data types, strong
compile-time checking of both types and interfaces, procedure and coroutine
control mechanisms, and control structures for dealing with
concurrency and exceptional conditions.
XEROX
PALO ALTO RESEARCH CENTER SYSTEMS DEVELOPMENT DEPARTMENT
3333
Coyote Hill Road / Palo Alto / California 94304
© Copyright 1979 by Xerox Corporation
CHAPTER 1. INTRODUCTION
1.1. Syntax notation
 CHAPTER 2. BASIC DATA TYPES AND EXPRESSIONS
CHAPTER 2. BASIC DATA TYPES AND EXPRESSIONS
2.1.
A slice of Mesa code
2.1.1. Basic lexical structure 2.2.
Simple declarations
2.3. The fundamental operations. 4-, and #
2.4.
Basic types
2.4.1.
The numeric types INTEGER
and CARDINAL
2.4.1.1. Numeric literals 2.4.2. Type BOOLEAN
2.4.3.
Type CHARACTER
2.4.4.
The numeric types LONG
INTEGER and LONG CARDINAL 2.4.5. Type REAL
2.4.6. Relations among. basic types 2.5.
Expressions
2.5.1.
Numeric operators
2.5.1.1.
Domains of the numeric operators
2.5.1.2.
The operator LONG
2.5.1.3. CHARACTER operators 2.5.2. Relational operators
2.5.3. BOOLEAN operators 2.5.4. Assignment
expressions 2.5.5. Operator precedence
2.6. Initializing variables in declarations
2.6.1. Compile-time constants
2.7. More general declarations
CHAPTER 3. COMMON CONSTRUCTED DATA TYPES
3.1. The element types
3.1.1.
Enumerated types 3.1.2. Subrange types
3.1.2.1.
Subranges of numeric types
3.1.2.2. Range assertions 3.2. Arrays
3.2.1. Declaration of arrays 3.2.2.
Array constructors 3.3. Records
3.3.1.
Field lists
3.3.2.
Declaration of records 3.3.3. Qualified references 3.3.4. Record
Constructors 3.3.5. Default field values 3.3.6.
Extractors
3.4.
Pointers
3.4.1.
Constructing pointer types 3.4.2. Pointer operations 3.4.3.
Long Pointers
3.4.4. Automatic derefcrencing
 3.5. Type determination
3.5. Type determination
3.5.1.
Type conversion
3.5.2.
Balancing
3.5.3.
Free conformance
3.6. Determination of representation
CHAPTER 4. ORDINARY STATEMENTS
4.1. Assignment
statements
4.1.1.
Assignment expressions
4.2. IF statements
4.2.1. IF expressions 4.3. SELECT statements
4.3.1. Forms and options for SELECT
4.3.2.
The NULL statement
4.3.3. SELECT expressions
4.4. Blocks
4.4.1.
GOTO statements
4.4.2. OPEN clauses
4.5. Loop statements 4.5.1. Loop
control
4.5.2. GOTOS, LOOPS, EXITS, and loops
CHAPTER 5. PROCEDURES
5.1. Procedure
types
5.1.1.
Procedure values and compatibility
5.2.
Procedure calls
5.2.1. Arguments and parameters
5.2.2.
Termination and results
5.3.
Procedure bodies
5.3.1.
RETURN statements
5.4. A
package of procedures
5.4.1. The example
5.4.2.
Invoking procedures in other modules
5.5. Nested
procedures
5.5.1.
Scopes defined by procedures
5.6. Inline
procedures
CHAPTER 6. STRINGS, ARRAY DESCRIPTORS, RELATIVE POINTERS, AND VARIANT RECORDS
6.1. Strings
6.1.1.
Strine literals and string expressions
6.1.2.
Declaring strings
6.1.3.
Long strings
6.2. Array
descriptors
6.2.1.
Array descriptor types 6.2.2. Long descriptors
6.3.
Base and relative pointers
6.3.1.
Syntax for base and relative pointers
6.3.2.
A relative pointer example 6.3.3. Relative pointer types 6.3.4.
Relative array descriptors
6.4. Variant
records
6.4.1.
Declaring variant records 6.4.2. Bound variant types
 6.4.3. Accessing entire variant parts. and '
ariant constructors 6.4.4. Accessing components of
variants
6.4.3. Accessing entire variant parts. and '
ariant constructors 6.4.4. Accessing components of
variants
CHAPTER 7. MODULES, PROGRAMS, AND CONFIGURATIONS 7.1.
Interfaces
7.2.
The fundamentals of !lesa modules
7.1.1.
Including modules: the DIRECTORY
clause
7.2.1.1. Enumerating items from an included module: the USING clause
7.1.1. Accessing items from an included module
7.2.2.1.
Qualification
7.2.1.2.
OPEN clauses
7.2.3. Scopes for identifiers in a module
7.2.4.
Implications of recompiling included modules
7.3.
DEFINITIONS modules
7.3.1.
Interface variables
7.3.2.
Default fields in interfaces
7.3.3. lnline procedures in interfaces
7.3.4.
Usage hints for inline procedures in interfaces
7.4.
PROGRAM modules:
IMPORTS and
EXPORTS
7.4.1. IMPORTS, interface types, and
interface records
7.4.2.
Importing program modules
7.4.3.
Exporting interfaces and program modules
7.4.4.
IMPORTS in DEFINITIONS
modules
7.5. Controlling module interfaces: PUBLIC and
PRIVATE
7.5.1.
Access attributes in declarations
7.5.1.1.
Declared names
7.5.1.2. Names specified in field lists
7.5.1.3. Names for variant parts and for tags in variant
records 7.5.2. Access attributes in TYPE definitions
7.5.3. Default global access
7.5.4. Accessing the PRIVATE predefined symbols of other
modules 7.6. The Mesa configuration language. an introductory example 7.6.1.
Lexicon: a module implementing LexiconDefs
7.6.2.
LexiconClient: a client module
7.6.3. Binding, loading, and running a configuration: an
overview 7.6.4. A configuration description for running
LexiconClient 7.7. C/111esa: syntax and semantics
7.7.1.
IMPORTS, EXPORTS, and
DIRECTORY in
C/Mesa
7.7.2.
Explicit naming. IMPORTS,
and EXPORTS
7.7.3.
Default names for interfaces and instances
7.7.4. Multiple exported interfaces from a single
component 7.7.5. Multiple components implementing a single interface
7.7.6. Nested (local) configurations
7.8.
Loading modules and configurations: NEW and START
7.8.1.
The NEW operation
for making copies of modules 7.8.2. How the loader binds
interfaces
7.8.3.
STARTing, sToPping,
and RESTARTing module
instances 7.8.4. Loading
and starting configurations
CHAPTER 8. SIGNALLING AND SIGNAL DATA TYPES 8.1.
Declaring and generating SIGNALS and ERRORS 8.1.1. ERROR in expressions
8.2.
Control of generated signals
8.2.1. Preparing to catch signals: catch phrases
 8.2.2. The scope of variables in catch phrases 8.2.3.
Catching signals
8.2.2. The scope of variables in catch phrases 8.2.3.
Catching signals
8.2.4. RETRY and CONTINUE in catch phrases 8.2.5.
Resuming from a catch phrase: RESUME 8.3. Signals within signals
CHAPTER
9. PORTS AND CONTROL STRUCTURES
9.1. Syntax and an example of PORTS
9.2. Creating and starting coroutines
9.2.1. The CONNECT statement
9.2.2. Low-level actions for a PORT call 9.2.3.
Control faults and linkage faults 9.2.4. Saving arguments
during faults
9.3.
RESPONDING PORTS
CHAPTER 10. PROCESSES
AND CONCURRENCY
10.1.
Concurrent execution. FORK
and JOIN
10.1.1. A process example
10.1.2.
Process language constructs
10.2.
Monitors
10.2.1.
An overview of monitors 10.2.2. Monitor locks
10.2.3.
Declaring monitor modules, ENTRY and INTERNAL procedures 10.2.4. Interfaces to
monitors
10.2.5. Interactions of processes and monitors
10.3.
Condition variables
10.3.1. Wait, notify, and broadcast
10.3.2.
Timeouts
10.4. 1Alore about monitors 10.4.1.
The LOCKS clause
10.4.2. Monitored records
10.4.3.
Monitors and module instances
10.4.4.
Multi-module monitors 10.4.5. Object monitors
10.4.6.
Explicit declaration of monitor locks
10.4.7. lnline ENTRY procedures 10.5. Signals
10.5.1. Signals and processes 10.5.2.
Signals and monitors 10.6. Initialization
APPENDICES
A.  Pronouncing Mesa
Pronouncing Mesa
B. Programming
Conventions
B.1.
Names
B.2.
Layout B.3. Spaces
C. Alto/Mesa Machine Dependencies
C.1. Numeric
limits
C.2. AltoDefs
C.3. ASCII
character set and ordering of character values
C.4. Alto/Mesa
STRING procedures
D.  Binder Extensions
Binder Extensions
Di Code packing 1).1.1. Syntax 1).1.2.
Restrictions
112. External links 1/2.1. Syntax 112.2.
Restrictions
E. Mesa
Reserved Words F. Collected Grammar
INDEX
This
document describes the Mesa programming language. Its
approach is tutorial, and it is intended to be read
somewhat as a textbook. It is neither a user's guide nor a reference manual.
Elements of
Mesa Style, by James Morris. is a recommended supplement to
this manual. The style manual contains several examples of
well-constructed Mesa programs, with explanations of their development
and commentary on using the language properly. Its purpose is to
provide assistance in using the features of Mesa to write programs
that work reliably and are easily maintained.
Programmers. should also read the Mesa Users Handbook, which
provides an introduction to the use of the Mesa system and a
guide to other documentation. The Mesa
System Documentation and Mesa
Debugger Documentation describe facilities available in the Alto
implementation of the Mesa programming system. These include input and
output, which are done procedurally and are not built into the
language.
Suggestions, corrections and criticisms concerning the
style and content of this manual are encouraged and
should be sent to your support group.
Acknowledgements
The
Mesa language was designed and first implemented by the Computer Science
Laboratory of the Xerox Palo Alto Research Center. The principal
participants were Butler Lampson, James Mitchell,
Edwin Satterthwaite, Charles Geschke, and Richard
Sweet. Subsequent
development and
maintenance
of the language and compiler have been done by the Systems Development
Department of Xerox. In addition to the original participants, John Wick and
Richard Johnsson have made major contributions.
The original version of this manual was written by
William Maybury and edited by James Mitchell. To reflect changes
in the language, many sections have since been added or revised. James Mitchell
and Richard Sweet have served as editors, with additional
contributions by Edwin Satterthwaite, John Wick and Richard
Johnsson. David Redell wrote most of Chapter 10.
Vicki Parish, Gail Pilkington, Janet Farness, and Ode
Binkley helped greatly with manuscript preparation and formatting:
Gail Pilkington, James Sandman, Barbara Koalkin, and Bruce Malasky assisted
in proofreading and indexing.
CHAPTER
1.
INTRODUCTION
This manual concentrates on the Mesa programming
language. Mesa is really a programming system of which the
language is but one part. Other components of the system are documented
separately, as are the details of preparing, compiling, debugging and
running Mesa programs.
Each chapter of this manual discusses some aspect of the
language, using examples as well as descriptions of semantics
and syntax. The chapters emphasize different language features and provide
different levels of detail. The complete treatment of some features requires
more than one chapter. Generally, earlier chapters introduce
topics, and later ones supply additional detail. Titles of
chapters, sections and subsections indicate the language issues with which they
deal.
In each major section, information is presented
at three levels:
(1)
Ordinary usage (motivation, forms and
semantics), frequently with examples.
(2)
Syntax equations (when appropriate).
(3) Fine points (if
applicable): restrictions, special cases, references to later material, precise
semantics, etc.
Level (1) is intended to offer a basic understanding of
Mesa. Reading only first level material should be adequate to begin
programming in the language. Levels (2) and (3) supply more detail and
provide information about the full power of Mesa.
As a rule. these levels of discourse occur separately and
in the indicated order. A section with a heading followed by an
asterisk (*) deals with specialized material that can be skimmed or skipped entirely
on first reading. Occasionally, fine points or syntactic details are presented
within first-level material. The reader will be able to distinguish
between levels by their appearance. Fine points are written
in a small font. like this. Syntax
equations and syntactic categories appear in the following font: FontForSyntax.
Any italicized word or phrase is important. If
a Mesa technical term is being introduced, it will be in italics:
if a term is used before being defined, it will be italicized to warn the
reader that it should not be taken lightly and that it has a particular
meaning in Mesa. Occurrences of a technical term, once
defined, are not distinguished. Lastly, names appearing in programs are
italicized in both the program text itself and the explanations of that
text.
Programming examples are indented relative to the
surrounding text to distinguish them.
1.1. Syntax notation
Mesa's grammar is described by syntax equations
written using a variation of Backus-Naur Form (or BNI). For those unfamiliar with
BNF, an explanation follows. Reading and understanding that explanation
is imperative for full use of this manual; in a first reading. details of the
syntax equations can safely be skipped. Those familiar with BNF
should scan this section to discover the particular variation being used.
An individual syntax equation defines a portion
of the Mesa _grammar. It specifies a rule for forming
some class of phrases in the language. A phrase class has a name. e.g., Program. and is defined
by one or more syntax equations. Phrase names are always printed in the syntax
font when their use is meant to be technically accurate. For
example, an OctalDigit, which can be any of 0, 1,
2, . . 7, is defined by
the equation:
OctalDigit :: =
011121314151617
Each equation consists of a phrase name on the left,
followed by the operator :: (which should be pronounced is
defined to be"), in turn followed by a formation rule for that phrase class A formation
rule consists of one or more alternatives,
separted by the syntactic operator vertical bar, I (which
should be pronounced "or"). The ordering of alternatives is not
important. In the definition of OctalDigit,
"3" is an alternative.
Each alternative is a sequence of symbols, where a symbol is either a
phrase name (in the syntax font) or a syntactic literal. In a syntax
equation, a literal symbol stands for itself. The reserved words
of Mesa, such as BEGIN, appear as literals; they
are always written using upper-case characters
in the font shown. The digits 0, 1, 2, etc. and special
characters, such as =, + and also are used to form literal
symbols. Some composite symbols are formed from more than one special
character, e.g., =>. Spaces in syntax equations are used only to
separate the items in the rules and have no special
significance.
The phrase name empty is
often used as one of the alternatives in a formation rule. It means that
the rule permits an ''empty" phrase as one of its
alternatives (i.e., an actual phrase is optional; it
may or may not
occur in
the result of applying the formation rule).
Comments embedded in syntax
rules are preceded by a double dash. --, and appear to the right, e.g.,
Digit =
OctalDigit 1819 -- a decimal digit is
an OctalDigit
or
an
8 or a 9
Often, only part of the total definition of a phrase
class is given. To indicate that there are other ways of forming
phrases of that class, an ellipsis (...) is used as an alternative within the
rule. The definition of Statement is distributed throughout
much of the manual in this way. When a certain statement form,
such as the AssignmentStmt, is being discussed, the following partial
rule appears:
Statement = AssignmentStmt
I -- this
is just an example.
One can read this as, "A Statement is
defined to be an AssignmentStmt, among other things."
Within a single alternative, the order of symbols is
important. The alternative acts as a "template" for
forming an actual phrase; literal names and literal characters are copied, while substitutions are made
for the phrase names. Consider the following example:
ReturnStmt = RETURN I RETURN Constructor
("A
ReturnStmt is defined to be RETURN or RETURN followed by a Constructor.")
The second alternative means that RETURN and
some actual phrase defined by Constructor occur in exactly that
order.
Syntax equations can indicate recursive substitution: for example:
IdList =
identifier I identifier , IdList
In a Mesa program,
an identifier is basically a name. This equation defines an IdList to
be a list of one or more names, with commas separating them if
there is more than a single name in the list.
This result is explained as follows. The
formation rule for IdList consists of two alternative rules:
Rule 1: (First alternative) "An
IdList is defined to be an identifier". i.e.. any one name can replace an IdList
Rule
2: (Second alternative) "An IdList is defined to be an
identifier followed by a comma followed by another IdList". i.e.. name. IdList
can replace an IdList.
To
derive a single name. use Rule 1 as shown below. (Note: The substitutions are
emphasized by writing them in italics.)
IdList ::= name (by Rule 1)
To
derive two names separated by a comma:
IdList ::= name, IdList (by Rule 2)
name, name (by Rule 1)
To
derive three names separated by commas:
IdList ::= name, IdList (by Rule
name, name, IdList (by
Rule
name. name, name (by
Rule
To derive n names separated by commas. use Rule 2
2)
2) 1)
n-1 times and then use Rule 1.
The following syntax equation also relies on recursion:
StmtSeries =
empty I Statement I Statement ; StmtSeries
The
equation is read as, "A StmtSeries is defined to be empty, or a
single statement, or a series of statements separated by
semicolons: the last statement may be followed by a semicolon."
A
trailing semicolon is possible because:
1)
A StmtSeries may take
the form specified by the third alternative. "Statement : StmtSeries".
2) After some number of further
substitutions using the third alternative. the recursive reference to
StmtSeries may take
the "empty" form. i.e.. ".. Statement :
empty".
3) empty is replaced by nothing at all, i.e.,
"... Statement :".
Commas and semicolons are used as major separators for a
variety of constructs in Mesa. To distinguish between such
constructs, a convention is adopted that the suffix "List" on a
phrase name implies a sequence separated by commas, while.
"Series" implies a sequence separated by semicolons.
This convention is reflected by the phrase names IdList and StmtSeries
above.
CHAPTER
2.
BASIC DATA TYPES AND EXPRESSIONS
This chapter presents some of the fundamentals of Mesa. It
discusses how to declare, initialize and assign values to variables. It also
describes the basic types for numeric, character and Boolean data, as
well as the operators used to construct expressions having these types.
The Mesa language is strongly typed. The programmer is given a collection of
predefined types and the ability to construct new ones; he is
encouraged to choose or invent suitable types for each particular
application. Every variable used in a Mesa program must be declared to have one of these
types; every constant has a type; and every expression has a type derived from
its components and context. All types can be deduced by static
analysis of the program, and the language requires that
each value be used in a way consistent with its type according to rules
specified here and in chapter 3. The type of an object determines its
representation and structure as well as the set of applicable
operations. In addition, the type system can be used to partition the universe
of objects and avoid confusion, even among classes of objects that
are represented identically.
2.1. A slice of Mesa code
The example below is an excerpt from a Mesa program. It
assigns to gcd the
greatest common divisor (GCD) of a pair of integers. in and n (where in, n and gcd are integer variables in the
program from which this excerpt was taken; we assume their
values need not be preserved). The example uses the Euclidean
Algorithm for finding the GCD of two numbers and works as follows:
If both in and n
are zero, the GCD is zero (by convention).
Otherwise, repeat the following until ii is zero: find the remainder
of dividing in by
set in to
the value of n: then
set n to
the remainder. The final value of in
is the GCD of the original in and n except that it may be
negative; taking its absolute value gives the GCD.
Example. Slice of Mesa Code Using the
Euclidean Algorithm
|
-- Given are integers in and n, which can be altered.
|
(1)
|
|
IF 111=0 AND 11=0 THEN gcd 4-
0 -- by
convention
|
(2)
|
|
ELSE
|
(3)
|
|
BEGIN
|
(4)
|
|
r: INTEGER;
|
(5)
|
|
UNTIL n= 0
|
(6)
|
|
DO
|
(7)
|
|
r in
MOD n: r gets remainder of in/
|
(8)
|
|
in 4- 12: n r -- update variables
|
(9)
|
|
ENDLOOP ;
|
(10)
|
|
gcd -- in case one of in or n was negative -- ABS[nij:
|
(11)
|
|
END;
|
(12)
|
The example contains twelve lines of source code.
including comments. The numbers in parentheses at
the right side are for reference only and are not part of the source-code.
Comments begin with the symbol
"--" and terminate at line endings. They may also be completely
embedded within lines, in which case they both begin and end with
"--''.
Line (2) begins an IF statement that uses
the values of in and to
select between two alternatives. If
both values are zero, the assignment statement following THEN is
executed: it assigns the value 0 to
gcd (the
character ".-." is Mesa's assignment operator). If either is nonzero.
the assignment is skipped and the compound statement following ELSE (lines (4) through
(12) inclusive) is executed. (Distinguishing
the two cases is actually unnecessary, but doing so illustrates more features
of Mesa.)
The second alternative is a block, a series of
declarations followed by a series of statements, all bracketed
by "BEGIN" and
"END". Line
(5) declares a variable r of
type INTEGER for
use within that block. A semicolon separates the declaration from the
statements that follow it.
The iteration in the algorithm is performed by the loop (UNTIL n=0
DO...ENDLOOP). which
contains three embedded assignment statements. The loop repeats
until n is
equal to zero. If it is zero at the outset, the embedded
statements are not executed at all. Statements are separated by semicolons. A semicolon
at the end of a statement series that is embedded in another statement (such as
the series in the loop) is optional; it is permissible to write a
semicolon after every statement
in the series.
Within the loop, line (8) assigns to r the value of the expression "In MOD a", which
gives the remainder of dividing in by n.
Line (9) updates In to
contain the previous value of n and then updates n for the next iteration, if
any. Control transfers from the end of the loop, line (10), back to line
(6), where the new value of n is
tested. If it is not zero, the loop is repeated; otherwise, execution
continues with the first statement following the
loop, line (11).
When control reaches the assignment statement in line
(11), in either
has its original value (if 17 was
zero) or contains the value a had just before it became
zero. The expression "Aes[n]" has the form used
for calling a function and passing it one or more arguments; square
brackets enclose the
argument list. Normal parentheses, "("
and '')". are used
only for nested expressions, e.g.,
"a*(b+c/(d— e)*f)." The
assignment places the absolute value of i» into gcd; this is the correct
result. At this point, the reader is urged
to trace through the example with initial values for m and
n of
15 and 12, respectively; the result should be gcd=3.
2.1.1. Basic
lexical structure
The
names gcd. in, n and
r in
the example are called identifiers. The general form of an identifier
is given by the following (informal) syntax:
An identifier is a sequence consisting of' any
mixture of upper-case letters, lower-case letters or digits, the
first of which is a letter. Upper and lower case letters are different and do
distinguish identifiers.
The following, valid identifiers are
all distinct:
aBc Abc
DiskCommandWord display Vector mach 1 x32y40
Identifiers consisting entirely of capital letters are
reserved for use by the Mesa language. Some, / such as IF, are punctuation
symbols: others name built-in types. such as INTEGER, or functions, such as
ABS. All
such words that have special meaning and are not to be defined by
the programmer are
called reserved
words. It is legal for the programmer to use fully
capitalized identifiers, but he risks a clash with a reserved word
(possibly a new one in some future version of the language). To avoid this.
at least one digit or lower case letter should appear in any identifier.
Appendix E lists the current set of reserved words.
Mesa uses the blank
(or space) character to separate basic lexical units of the language (such as reserved
words and identifiers). Blanks are
significant separators of lexical units. They may not he embedded
in identifiers, composite symbols (such as >= ), or numeric literals (such
as 1000). Blanks are meaningful in STRING constants
(section 6.1.1). and there is a CHARACTER constant for space
(section 2.4.3). As a separator. any sequence of contiguous blanks
is equivalent to a single
blank. A TAB
character also behaves exactly as a blank when
used as a separator.
A carriage-return character behaves as
a blank for separating lexical units also, but it has one extra function:
if the last part of a line is a comment. the carriage return acts as
the terminator of that comment. Thus, multiline comments (those
containing carriage returns) must begin with "--" on each
new line. Line breaks have no significance as statement separators.
For example, the single loop statement in the example extends over a
number of lines, and a semicolon is used to separate two
statements in a series.
Semicolons are used
for separating declarations, for separating a series of declarations from
following statements, and for separating statements in a series from one
another. They cannot be used with abandon, however: care is necessary when writing IF statements (sec. 4.2.1) or SELECT statements (sec. 9.3.1). Multiple statements can be written on a single line, separated by
semicolons.
2.2.. Simple
declarations
The example (Euclidean Algorithm) contains the following
declaration:
r: INTEGER:
This declares r to be a variable of type INTEGER (sec.
2.4.1), one of Mesa's built-in types. More than one variable can be
declared at the
same time. For instance,
x, y, divisor: INTEGER;
declares identifiers x, y and
divisor as
variables of type INTEGER. These examples reflect the
two primary purposes of every declaration:
to designate one or more identifiers as
variables, and to specify their type. -
A declaration always begins with a single
identifier or a list of identifiers. Conventionally. "list" is used
to denote a single item as well as multiple items separated by commas. An identifier list (IdList)
is defined as follows:
IdList = identifier I
identifier, IdList
A declaration begins with an IdList followed by a colon. The
colon is followed by a type specification (INTEGER, for
instance, is a type specification).
2.3. The fundamental operations: assignment, equality and
inequality The example contains the following five assignment
statements:
gcd 0
r ni MOD n
m 4- n
n 4- r
gcd ABS[M]
An assignment statement has the following syntax:
AssignmentStmt =
LeftSide 4-
RightSide I
...
LeftSide =
identifier I ... -- plus
forms for array indexing. etc.
RightSide = Expression
The
RightSide may
be any expression (section 2.5) provided that its type conforms to that of the LeftSide.
"Conforms" is defined in section 2.4.6 and is discussed further in
section 3.5: for now. it can be taken to mean: "is the same as."
The LeftSide may be a simple variable or a component of an
aggregate variable (such as an element of an array). In
any event. a LeftSide denotes a variable, something capable of
receiving values. A LeftSide cannot, for example, be a constant, while a
RightSide can.
The assignment operation ( <-.), the equality
operation (= ) and the inequality operation (#) are called the fundamental operations. They
can be applied to values of most types (including, for instance,
entire arrays). The rules governing which pairs of operands may be
used in a fundamental operation are detailed in section 3.5.
2.4. Basic types
The
types of variables in a Mesa program fall into two broad classifications, built-in types and user-defined
types. Chapter 3 describes how a programmer can define new
data types using type constructors. This section
discusses the basic, built-in types. These include several numeric types
(INTEGER, LONG INTEGER,
CARDINAL, LONG CARDINAL and REAL). a type for logical values (BOOLEAN), and
a type for individual character values (CHARACTER). The built-in type STRING (for
sequences of characters) is described in chapter 6.
2.4.1. The numeric types INTEGER and CARDINAL
Mesa provides two standard numeric types, one with values
ranging over the signed integers; the other,
over the unsigned integers. Neither type completely mirrors the
corresponding mathematical abstraction (the integers Z or the natural numbers N,
respectively) because a finite representation is used for values of
each type. The range of the type INTEGER is (approximately) symmetric
about zero, and values of type INTEGER are represented as signed numbers. The range of the
type CARDINAL is
some finite interval of the natural numbers that includes zero, and values of
type CARDINAL are
represented as unsigned numbers.
"Signed" and "unsigned" are not types; rather,
they describe the machine
representation of a numeric value.
The programmer must choose an appropriate type for each
numeric variable. CARDINALS
offer a somewhat greater
positive range than INTEGERS,
and this is significant in a few applications, e.g., those
that manipulate addresses that might be the same size as the word size. More
importantly, declaring a variable to have type CARDINAL asserts
that its value is always nonnegative; the compiler can
use such assertions to perform more checking and to generate better code.
Programmers are encouraged to declare as much information about
each variable as possible: the ranges of numeric variables can be
further constrained by using subrange types (section 3.1.2).
The types INTEGER and CARDINAL are distinct and not
interchangable. They are. however, closely related. Mesa
allows most combinations of these types to occur within assignments and
arithmetic expressions (but not relational expressions). Care is necessary to
avoid ambiguity and failures of representation when values
with different representations are mixed. This is discussed further in sections 2.4.6 and 2.5.1.1.
2.4.1.1. .Vumeric
literals
A !runlet* literal is
an instance of the phrase class number, defined as follows:
A number is a sequence of digits. The digits may
optionally be followed by the letter B or B. which in turn may
optionally be followed by another sequence of digits denoting a
scale factor. No spaces arc allowed within numeric literals.
If I) is specified explicitly, or if neither B nor I)
appears. the number
is treated as decimal. The letter 13 means
the number is
octal (radix 8). A scale factor indicates the number of zeros to be appended
to the first sequence of digits: the
scale factor itself is always a decimal number. The
literals below all denote the same value:
6400 MOOD 641)2 14400B 144B2
A numeric literal always denotes a nonnegative
number (i.e., — 5 is considered to be an expression in which
the unary negation operator is applied to the literal 5 to produce an INTEGER value).
To be valid in a context requiring a CARDINAL, the
value of the literal must be a valid CARDINAL number. Similarly,
if an INTEGER is
required by context, the value must be a valid (positive) INTEGER. (See
section 2.4.4 for more details)
2.4.2. Type BOOLEAN
A BOOLEAN value can be either TRUE or
FALSE,
and these are the only literals of type BOOLEAN: i.e., BooleanLiteral :: = FALSE I TRUE
BOOLEAN expressions
are used in conditional statements (following IF) and in certain loop
constructs. For instance, the
following skeletal form describes the flow of control in Example 1:
IF
n?=0 AND n=0 THEN . . . ELSE
. . .
UNTIL 17= 0
DO
. . .
ENDLOOP;
The
expression "n=0" is
a BOOLEAN expression:
its value is TRUE if
the value of n is
zero and FALSE otherwise.
The expression "m=0 AND n=0" is also a BOOLEAN expression: its value is TRUE just
if both relations are. The relational and logical
operators discussed in sections 2.5.2 and 2.5.3 all yield BOOLEAN values.
|
Variables of type BOOLEAN can be assigned values
and appear as operands (although arithmetic operators) just
as any other Mesa variables. For example, the above program could validly be
replaced by the following:
mIsZero. nlsZero: BOOLEAN;
mIsZero (m=0): nlsZero n=0: -- compute whether in and n are zero IF ,nlsZero AND nlsZero THEN . .
ELSE
• • •
|
not of outline
|
|
UNTIL nIsZero=
TRUE
DO
. . .
nlsZero n=0;
ENDLOOP;
|
-- equivalent to just nlsZero by itself
-- recompute whether n is zero just before testing
|
|
|
|
2.4.3. Tpe CHARACTER
A value of type CHARACTER represents a single character of text. CHARACTER values are ordered I (according
to the order specified in appendix C) and can be compared using the normal
arithmetic relations. CHARACTER values are distinct from numbers. and they cannot
be assigned to variables with numeric types. Limited arithmetic is, however, allowed on
characters (section 2.5.1.2).
A characterLiteral is
written as an apostrophe C) immediately followed by a single character (which
can be a blank, carriage-return, semicolon. apostrophe. or any other character)
or as an octal number followed by C. For example:
 lowerCaseA 'a: mark 4-
lowerCaseA 'a: mark 4-
enalarker asciiCR 4-
15C:
2.4.4. The numeric types LONG INTEGER and LONG CARDINAL *
For some applications, the ranges of the numeric types
introduced in section 2.4.1 are too limited. Mesa provides both
a predefined type LONG
INTEGER, with signed representation, and a predefined type
LONG CARDINAL, with
unsigned representation, for such applications. These types offer greater ranges.
but their values occupy more storage and are generally more
time-consuming to manipulate than those of the
previously introduced numeric types.
In an implementation, values of types INTEGER and
CARDINAL are
expected to be represented by single machine words, while
values of types LONG
INTEGER and LONG CARDINAL are expected to occupy two words.
For this reason, INTEGER
and CARDINAL will be referred to as short numeric types: LONG INTEGER and
LONG CARDINAL, as
long numeric types. On
a machine using two's complement
arithmetic and a word length of N bits, the following table indicates the range
spanned by each numeric type (".." replaces the
mathematician's comma in this interval notation):
INTEGER [—
2N-1
CARDINAL [0
.. 2N)
LONG
INTEGER [_2 22N-1)
LONG
CARDINAL [0
..
The actual ranges for these types are given
in appendix C. the machine dependencies appendix.
Long numeric constants are denoted by numeric literals
defined by the phrase class number (section
2.4.1.1). The allowable type of any decimal or octal literal is determined by
its value, as summarized by the following table (using
the conventions introduced in the preceding paragraph):
|
Range
[0 .. 2N-1)
[2N-1 .. 2N)
[2'..2211)
p2N-1 22N)
|
Allowable Types
INTEGER,
CARDINAL, LONG INTEGER, LONG CARDINAL CARDINAL, LONG INTEGER, LONG CARDINAL
LONG INTEGER. LONG CARDINAL
LONG CARDINAL
|
As in the case of short numeric types, the types LONG INTEGER and
LONG CARDINAL are
distinct but closely related. Mesa allows most combinations of
these types and the types INTEGER and CARDINAL to occur within assignments,
arithmetic expressions and relational expressions. but care is necessary when
this is done (see sections 2.4,6 and 2.5.1.1).
Type REAL (interim) *
The values of Mesa's type REAL are approximations
of mathematical real numbers. These approximations arc sometimes called floating-point numbers. For the
current version of Mesa. a standard representation for floating-point
values has not been chosen. The language nevertheless provides
some help with floating-point computation. It allows declaration and assignment
of REAL values, and REAL expressions constructed using the standard infix
operators are converted to
sequences of procedure applications by the compiler.
A REAL
value is assumed to occupy the same amount of storage
as a LONG INTEGER (i.e.,
two words). Beyond this, no assumptions are made about the
representation of REALS.
There are no literals with type REAL. Users
of real arithmetic must provide an appropriate set of procedures for performing
the arithmetic and relational operations.
Although Mesa provides no denotations of REAL literals,
it does provide automatic conversion from INTEGER, LONG INTEGER, CARDINAL or
LONG CARDINAL to REAL (section
2.4.6). Thus numbers (numeric literals) can
appear in REAL expressions
and provide denotations of certain REAL constants.
2.4.6. Relations among basic types *
If two types are completely interchangable,
they are said to be equivalent. A
value having a given type is acceptable in any context requiring a
value of any other type equivalent to it: there is no operational
difference between two equivalent types. None of the basic types discussed in
section 2.4 is equivalent to another basic type.
One type is said to conform to another if any value of
the first type can be assigned to a variable of the second type. A
type trivially conforms to itself or to any type equivalent to itself. In more interesting
cases, an automatic application of a conversion function may be required prior
to the assignment. Conformance
and its implications are discussed further in section 3.5.
There are nontrivial conformance relations involving the
types INTEGER, LONG
INTEGER, CARDINAL, LONG
CARDINAL and REAL. These relations allow certain combinations of
the numeric types to be mixed, not only in assignments but also in
arithmetic and relational operations (section 2.5). They also
permit these types to share denotations of constants (section 2.4.4). The
conformance relations can be summarized as follows:
INTEGER
and CARDINAL conform to INTEGER.
INTEGER
and CARDINAL conform to CARDINAL.
INTEGER,
LONG INTEGER, CARDINAL and LONG CARDINAL conform
to LONG
INTEGER. INTEGER, LONG INTEGER, CARDINAL and LONG CARDINAL conform
to LONG
CARDINAL. INTEGER, LONG INTEGER, CARDINAL, LONG CARDINAL and
REAL conform
to REAL.
Pairs of numeric types not on this list do not conform:
e.g., it is not possible to assign a LONG
INTEGER to an INTEGER or
a REAL to
a CARDINAL.
Particular care is required when numeric types with
different representations are intermixed. Mathematically, Z D N: however. it is not
necessarily true that INTEGER
D CARDINAL
or that LONG INTEGER D
LONG CARDINAL. For
instance, with the assumptions above, the intersection of INTEGER and
CARDINAL is
[0..2/v-1). Within this interval, the signed and unsigned representations
agree. and the interpretation of a short numeric value is
unambiguous. If a CARDINAL value lies in this range, it can validly be .assigned to an INTEGER variable, and vice-versa: outside this range, the
value represented
w
by a given
word depends upon whether it is viewed as a CARDINAL or as an INTEGER. Similar
considerations apply to LONG CARDINAL and LONG INTEGER.
Example:
With the assumptions above and A1=16, the
unsigned value 177777B and the signed value — 1 are encoded by the
same bit pattern.
Assignment of an unsigned value to an INTEGER variable.
or of a signed value to a CARDINAL variable. implicitly invokes a conversion function,
which is just an assertion that the value to be assigned is an
element of CARDINAL fl INTEGER. It is the
responsibility of the programmer to ensure that the conversion is valid. In many cases this is not
too difficult, but programmers are urged to avoid mixing signed
and unsigned representations when this is possible. It almost always is.
Mesa does guarantee that LONG T D T for
any type T and
that LONG INTEGER 3 CARDINAL;
thus it is always valid to assign a
short numeric value to a LONG INTEGER variable or a short unsigned value to
a LONG CARDINAL variable.
The properties of conversion to type REAL are not specified by the language.
Some
fine points:
A user supplied
procedure FLOAT is automatically applied to
convert a value from type LONG INTEGER to REAL. Short numeric values
are converted first to LONG INTEGER and then to REAL.
Conversion from a
short numeric value to a LONG INTEGER (and thus to a REAL) is substantially
more efficient when
the value has an unsigned representation.
The conversion of a constant to type
REAL occurs even time the containing expression is evaluated at run-time.
Neither BOOLEAN nor CHARACTER conforms
to any other basic type.
|
Examples:
INTEGER:
(valid)
|
n: CARDINAL; LONG INTEGER; x: REAL;
i 4 0;
ii 0:
x F n;
x ii;
|
(invalid) i x:
11 4- TRUE;
2.5. Expressions
Expressions
are constructs describing rules of computation for evaluating variables and for
generating new values by the application of operators. The overall
syntactic rule for an expression is given by
Expression =
Disjunction AssignmentExpr IfExpr I SelectExpr ...
The Disjunction form includes all the numeric
operations, relational operations, and BOOLEAN (logical) operations and is
discussed in this section. An AssignmentExpr allows one to write multiple
assignments in a single statement and is discussed in section 2.5.4. The IfExpr
and SelectExpr forms are discussed in
chapter 4.
The basic unit from which expressions are built is called
a Primary. This syntactic class includes references to
variables, literals, function calls (chapter 5), and any arbitrary expressions
embedded in parentheses:
Primary =
Variable I Literal I( Expression ) FunctionCall I
Variable = LeftSide
Literal =
numbers BooleanLiteral characterLiteral
FunctionCall =
BuiltinCall I Call
-- defined in chapter 5
Recall that every expression has a well-defined type in
Mesa. The general rules for determining the type of an
expression from the types of its constituent parts are given in section 3.5. In
this section. the types of the basic expression forms (as functions
of the types of their operands) will be outlined. For
example, the type of a Primary is the type of the Variable or Literal
involved• or reduces to the type of the Expression
within parentheses, or is the type of the value returned by the BuiltinCall
(some of which are defined below) or the Call of a
user-defined procedure (section 5.1).
A Primary can be of almost any type; this
is not true of most of the expression forms built up using
Mesa's operators. Some operators are numeric and some are BOOLEAN. The
next sections discuss the numeric operations, the relational
operations, and the operations applicable only to BOOLEAN values.
Considered together, the operators form a single hierarchy with respect to
their precedence, which is
described with each
operator class and summarized in section 2.5.5.
2.5.1. Numeric operators
The
operations on numeric values are addition, subtraction, multiplication,
division, modulus, and arithmetic negation. The syntax for this group
of operations is
Factor =
Primary I — Primary -- negation
Product = Factor I Product MultiplyingOperator
Factor
MultiplyingOperator = *I / I MOD
Sum =
Product I Sum
AddingOperator Product
AddingOperator = + I —
These operators have their usual mathematical meanings.
The division operation on integers, /. always truncates toward
zero: thus —(i/ j)= — i/ j= / — j. The
MOD operator
yields the remainder of dividing one number by another (MOD is not applicable
to REAL operands).
MOD is
defined by the relation (i/j)*j+(i MOD
j) = i, and
the sign of the result of MOD is always the sign of the dividend. (This
is the reason that line 11 of Example 1 takes the absolute value of the
computed gcd: if
m= —12 and n=8 initially, the gcd would be —4 if its absolute
value were not taken.)
The built-in function MIN computes the minimum value in a list of
expressions; similarly, the MAX function, the maximum value. The
built-in function ABS computes
the absolute value of its
argument. The syntax for calls on the built-in functions is
BuiltinCall = MIN [ ExpressionList
MAX [ ExpressionList
ABS [Expression ]
. -- other built-in
functions later
ExpressionList = Expression I ExpressionList , Expression
For the arithmetic operators and built-in functions. the
order in which the operands are evaluated is undefined, but the
syntax implies a precedence ordering that controls the association of operators
with their operands. In that ordering. unary negation precedes the multiplying
operators, which in turn precede the adding operators. Sequences of operators of the same precedence
associate from left to right (with
the exception of the embedded assignment operator, section 2.5.4). Thus, an
expression such as a+b*—c does not
specify the order of evaluation of a. b and c but does require that the
operations be performed in the following order: negate c: then multiply the
result by b; finally,
add that result to the value of a.
|
Examples:
1. j. k: INTEGER; in, n: CARDINAL;
Factors: ri
15
(i+j+ k)
—15
ma+, j,
k, —15]
Products: /en
i/-15 15
n MOD 8
m/
n*10
—
k*(i+ 1)/2 moo 3
Sums: 1+1
—
i+j
i
n— n MOD 8 in — m/ n*n
|
-- same as (m/ n)*10 because of left-associativity -- same as a( —
k)*(i+1))/2) MOD 3
-- same as n—(n MOD 8) because of precedence -- same as m MOD n
|
2.5.1.1. Domains
of the numeric operators
In principle, each arithmetic operator designates the
corresponding mathematical function. Unfortunately, the hardware
underlying any implementation of Mesa does not provide this function but
only a set of related partial functions. For each operator, the compiler must
choose as appropriately as possible from this set. The choice is
made by considering the types of the operands.
Example:
With the usual assumptions. 177777B and —1 are represented
by the same bit pattern. The value of 177777B > 0 is TRUE, but that of —1 > 0 is FALSE.
Mesa provides the operators +, *, /, MIN. Max and ABS for all the numeric types. The operation moo
is defined for all numeric types except REAL; the operation of unary negation. for all but CARDINAL and
LONG CARDINAL. For
each of these operators. the type of the result is the same as the
type of the operands. In addition, the result of the
operation is considered to have signed representation if all the
operands have signed representation, and to have unsigned representation if all
the operands have unsigned representation. Thus, adding two INTEGER values
yields an INTEGER result,
and dividing one CARDINAL
by another yields a CARDINAL result.
Some
fine points:
Division and modulus operations on
short numeric values are substantialh more efficient if their operands are unsiened.
Addition. subtraction. and
comparison of lone numeric values are fast: multiplication and division are
done by software and
are relatively slow.
Operations upon REAL values are
implemented as calls on user-supplied procedures. These procedures must be assignable to variables declared
as follows {chapter 5):
FADD, FSUB. FM UL. FDIV: PROCEDURE [REAL, REAL] RETURNS [REAL]:
FCOMP: PROCEDURE [REAL, REAL] RETURNS [INTEGER]:
-- returns a value that is: 0 if equal.
negative if the first is less, positive otherwise
FLOAT: PROCEDURE [LONG
INTEGER] RETURNS [REAL]:
All
other REAL arithmetic operations are fabricated from these primitives.
Although the mathematical
integers (Z) and real numbers are closed under all these operations (except division by zero), the subranges defining the
types INTEGER.,
LONG INTEGER,
CARDINAL and LONG CARDINAL generally are
not. When the result of an operation falls outside the range of its assumed
type, a representational failure called overflow or underflon occurs. In the
current version of Mesa, ii is the programmer's
responsibility to guard against ovollow and undorflow
conditions.
The implications of
Mesa's conventions for subtraction are worth
emphasizing. If both operands have valid signed representations,
the result has a signed
representation. If both have only unsigned representations,
the result has an unsigned
representation and is considered to overflow if
the first operand is less than the
second.
Example:
INTEGER: m, n: CARDINAL;
I m— n: -- should be used
only if it is known that m >= n
i IF n7 > n THEN 277— n ELSE — (n — 1n); -- a safer form (section
3.6)
The arithmetic operations are defined for operands that all have the same
type, but it is possible to mix numeric types (and thus
representations) within an expression.
In this case, operands are convened as
necessary to the "smallest" type to which
all the operands conform, the operation for that
type is applied, and the result also has that type. The rule for expressions involving type REAL is
easy to state:
If any operand has type REAL, the REAL operation is used.
The rules governing
combination of numeric operands with differing representations involve some additional
concepts and are stated in section
3.6. Again, the programmer should try to
avoid such combinations when possible. (Recall that
literals in
INTEGER n CARDINAL have whatever representation
is required by context.)
2.5.1.2. The
operator LONG
The built-in function LONG converts any value with a short numeric type to a long numeric type. A value with an unsigned
representation is converted to LONG CARDINAL; one with a signed
representation, to LONG INTEGER, The
syntax is as follows:
BuiltinCall ,.. I LONG [ Expression ]
This operation is necessary
when the standard conversion rules do
not give the desired result. It can also be used to emphasize
the conversion.
Example:
LON G[ni* n] -- "short" multiplication, overflow lost
LONG[nd*LCNG[n] -- "long" multiplication
Some fine points:
Lenethenima
a sinw.le-precision expression
is substantially more efficient if
that expression has an unsigned
representation.
The Mesa implementation
provides standard procedures (not part of
the languaae) for performing certain multiplication and division operations
in which the operands and results do not all have the same length. These procedures provide less
expensive equivalents of, e.g LONG[nirLONG[rd.
2.5.13. CHARACTER
opera/ors *
Limited
CHARACTER arithmetic
is possible and is sometimes useful for manipulating the encodings of
CHARACTER values.
The following arithmetic operations arc defined for operands of type
CHARACTER:
A CHARACTER value plus or minus a short
numeric value yields a CHARACTER value. Subtracting
two CHARACTER
values yields an INTEGER value.
No other arithmetic
operations on characters arc allowed. Since the results of character arithmetic
depend upon details of the character encoding.
such arithmetic should be used with discretion.
|
Examples:
c: CHARACTER: digit: INTEGER:
digit 4- c — -0;
c (- 'A + (c—'a)
2.5.2. Relational
operators
|
-- assumes c is lower case
|
The relational operators include = and #, <, <=
(less than or equal). >= (greater than or equal), >, and
their negatives (e.g., NOT<, —<. —>=, etc.). These
operators always yield BOOLEAN
results, depending on the truth or non-truth of the
relation expressed. The operators = and # apply to most
types: the others, to any ordered type
(i.e.. to any type whose values are considered to be ordered). Ordered types
include INTEGER, LONG
INTEGER, CARDINAL, LONG CARDINAL, REAL, BOOLEAN. CHARACTER (with the ordering given in
appendix C). enumerated types (section 3.1), and subranges
of ordered types (section 3.1).
The relational operators also include the composite
operator IN, which
takes a numeric value as its left operand and an interval as its right operand. Its
value is TRUE if
the left value lies in the interval and FALSE otherwise. The syntax for relational operators is
 Sum
I Sum RelationTail
Sum
I Sum RelationTail
RelationalOperator Sum
Not RelationalOperator Sum I
IN SubRange
Not IN
Su bRange


 (1<=
=
(1<=
=
— NOT
SubRangeTC --
explained in chapter 3
Interval ... -- explained in chapter 3
Expression ..
Expression ) ( Expression .. Expression ) (
Expression .. Expression ] [ Expression .. Expression ]
The extra syntax for Su bRange and Su bRangeTC is placed
here to be consistent with later uses of the class Interval in
chapter 3. The syntax for intervals follows mathematical notation: a square bracket
indicates the inclusion of the respective end point in the interval, while a
parenthesis indicates its exclusion. For example, the following
intervals all designate the range from —1 to 5 inclusive:
[—I 5] 1-1
.. 6) (-2
.. 6) (-2
.. 5]
In the above examples. –1 is the lower bound of each interval:
the upper bound is
5. The hounds of an interval are its end points, reeardless of
whether the interval is written as a closed. half-open or open one. The hounds
are not required to he constants. An interval with an upper bound less than its
lower is said to be empty: no
values lie in such an interval. For example, the following are all empty
intervals:
–2] [-1 ..
–I) (-2 .. –1) (-2 .. –2]
|
Examples: Relations:
|
n = 15
# n
I <= .1
(i < j)
= (1 < k) n IN [1 .. 5)
i NOT IN 1— 1 .. 5]
|
-- or m –= 11
= with two BOOLEAN operands
>= 1 and n < 5
-- only legal if i is signed (because –1 is)
|
A fine point:
The relational
operators, like the arithmetic operators, denote families of hardware
operations when they have numeric operands. Anain, there is one operation for each numeric type.
If there is a unique "smallest" type to which all the operands conform,
they are convened to that type as necessary and then the comparison is performed. There is no unambiguous
choice of such a type for numeric operands with different representations:
an attempt to compare two such values is an error. The precise
rules appear in section 3.5.
2.5.3. BOOLEAN operators
The operators NOT (logical
negation), AND and OR apply only to BOOLEAN values. The syntax
is
Negation = Relation I Not Relation
Conjunction = Negation I Conjunction
AND Negation
Disjunction = Conjunction I Disjunction OR Conjunction
NOT ?legates the logical value of a BOOLEAN expression.
p AND q has the value TRUE if
and only if both p and q are TRUE. p OR q is TRUE if
at least one of p or
q is TRUE.
When evaluating a Boolean expression. evaluation
of primaries is guaranteed to take place from left to
right. In the operation AND or OR, the second operand is evaluated only if the first
operand's value does not determine the value
of the expression.
A
fine point:
"x AND y" is equivalent to the IfExpr
"IF .v THEN v ELSE FALSE": i.e., when x is FALSE. y is not o aluated.
"x OR y" is equivalent to the
IfExpr ''IF x THEN TRUE ELSE y'': i.e.. when x is TRUE. y is not evaluated.
It is therefore safe
to have expressions of the form "x AND y". where y is defined only
when x is TRUE. e.g.. "x#0 AND c/ x > 2". or "p=NIL OR p1=0".
Examples:
Negations: NOT 1=15 -- same as
NOT(i=15)
–q q must be of type BOOLEAN
–(p AND q)
Conjunctions: 1 <= j AND j < k
p AND — g
i=5 AND j NOT IN [— 1..1]
Disjunctions: in>n OR in =15
–p OR –q
2.5.4. Assignment
expressions
The assignment operation can be embedded in other
expression forms. When it is. the result of the operation has the
type of the LeftSide and
the value received by the LeftSide in
the assignment. The "+-" operator has the lowest precedence
of any operator. Its syntax is the same as that of the
AssignmentStmt:
AssignmentExpr = LeftSide (- RightSide
If this form is used to perform multiple
assignments. it is important to note that "4-"
is right-associative. Thus. the
assignment expression a<--b4-b+1 first
assigns the value of b+1 to
b and
then assigns b's new value to a.
|
Examples: Assignment
|
Expressions:
m4-15 m4-n*-15
tw-n4-n+1 --
same
as m4-(n4-(n+1))
Hj+-(j+1) MOD n)*2 -- all these parentheses are necessary
|
Rules governing assignments of numeric values when the
types are not identical are summarized in section 2.4.6.
Fine
point:
Because the order of
evaluation of the primaries is not defined, expressons such as "(i< j) + (p- kF have unpredictable values
and should not be used.
2.5.5. Operator
precedence
The following table summarizes the precedences of the
unary and binary operators introduced in this section. The order
is from highest precedence (tightest binding of operands) to lowest; operators
on the same line have the same precedence.
-- unary negation
*, MOD
+, — --
subtraction
=, #, <=, >,
>=, IN
—, NOT
AND
OR
4-
Parentheses can be used to explicitly control the
association of operands with operators.
2.6. Initializing
variables in declarations
A
variable may be given an initial value in a declaration. For example, the
Boolean variable delimited could
be set initially FALSE
by using the declaration:
delimited: BOOLEAN 4-
FALSE:
Variables (of the same type) can be initialized
collectively:
11. nO: INTEGER 4- —7:
This declares two separate integer variables n and 110 and initializes each to —7.
Any
expression that could be used as the Rig htSide of an assignment can be
used to initialize a variable:
1: INTEGER 4- ABS[n]; -- this will set i
to 7
i.S'quared: INTEGER 4-
14 -- Squared is initialized to 49
j: INTEGER 4- i.S'quared— i+1: j
is initialized to 49— 7+ 1 = 43
All initializations shown so far have taken
"assignment" (or "4-") form. There is
another form. the "fixed" (or "=")
initialization. For
example.
octalRadix: INTEGER = 8;
This means that octalRadix is to have a fixed value. It is never valid as the LeftSide
of an assignment. We call octalRadix a constant because its value can never
change after it is initialized (recall that the number 8 is
called a literal). Normally.
the term "constant" will include the term "literal";
if the distinction is important, then "literal" will be used.
Initial values for fixed
initialization can be arbitrary expressions. Paraphrasing the earlier example:
i0: INTEGER = ABS[— octalRadix]: iOSquared: INTEGER = 10* i0: j0:
INTEGER = iOSquared— i0+1;
The initializing expression can use values that
are not known at compile time. In this example, if octalRadix did not have fixed
initialization, the values of la
iOSquared, and j0
would be computed and assigned at run-time.
Variables are initialized in the order of appearance in a declaration, and later
declarations can use variables initialized earlier, as shown by the example.
2.6.1. Compile-time constants
Wherever possible, the Mesa compiler evaluates expressions
containing only constants. If a variable is initialized
using the fixed form and the expression can be evaluated at compile time, then
that variable has a known value. Since it can never appear as
the LeftSide of an assignment operator, it too becomes a
compile-time constant (the variables i0, i0Squared. and JO
in the previous section are all
compile-time constants).
Example:
beta: INTEGER = 3;
alpha: INTEGER = beta— 1:
In this case, alpha
is a compile-time constant (with the value 2), since the
expression beta-1 involves
only compile-time constants. Compile-time constants need not occupy memory at
run-time; the compiler can replace references to compile-time constants, such
as alpha and
beta, by
their known values.
Some
fine points:
Knowledge of compile-time constant
values can also be exploited when analyzing expressions. processing other declarations. or generating
object code.
One side effect of this propagation of constants is that
the representation of a numeric constant is known at compile-time. For
instance. alpha above is declared to be an INTEGER. but
because its value is 2. it may also be used as a CARDINAL. However, declaring
the type of alpha determines what kind of arithmetic
(signed or unsiened) will be used to compute its value. whether at compile-time or
run-time (section 2.5.1).
In certain contexts. an expression is required
to yield a compile-time constant value. A (sub)expression denotes such a constant
if all the operands are compile-time constants and the operation is not one of
those listed below (current restrictions):
Conversion of
a numeric value to type REAL.
Any
arithmetic or relational operation with operands of type LONG INTEGER. LONG
CARDINAL or REAL.
Application of an function (chapter 5) other than a built-in
function.
The @ operation (section 3.4).
The SELECT operation
(section 4.3.31.
2.7. More general declarations
Preceding sections have introduced all the syntactic
components of a declaration. The general form is defined as follows:
Declaration :: = IdList :
TypeSpecification Initialization
For the moment, TypeSpecification is defined as one
of the built-in types: chapter 3 describes other forms of TypeSpecification.
TypeSpecification ::
= PredefinedType I .
PredefinedType =
INTEGER
I CARDINAL I
BOOLEAN I CHARACTER
LONG
INTEGER I LONG CARDINAL I REAL I
STRING I --
see chapter 6
WORD I -- see fine point below
UNSPECIFIED --
see fine point below
An Initialization is formally defined as follows:
Initialization :: = empty
<-
Expression
=
Expression
--other forms are given later
Fine
points:
The
predefined type WORD is provided to describe values on which bit-by-bit loaical
operations are to be performed. Currently. it is a synonym for CARDINAL.
The
predefined type UNSPECIFIED is a device for by-passing most type
checking. An UNSPECIFIED value is a single machine word. and it matches the type of any
object that occupies at most a single machine word. including INTEGER.
CARDINAL. CHARACTER. BOOLEAN. UNSPECIFIED, STRING. and any user-defined type (chapter 3) that fits in a single
machine word.
For numeric operations.
its representation is similarly fluid. If a CARDINAL and an UNSPECIFIED value
are the operands of
some arithmetic operation. then the UNSPECIFIED value is considered to be unsigned.
If an UNSPECIFIED is combined with a
signed value. it is treated as if it were signed too. If an UNSPECIFIED is
combined with an UNSPECIFIED. they are both treated as siened.
Less type checking is sacrificed by
using LOOPHOLE (section 3.5.1) than by declaring variables with type
UNSPECIFIED.
CHAPTER 3.
COMMON CONSTRUCTED DATA TYPES
Mesa encourages the programmer to augment the
collection of predefined types by constructing
new types. Types can be defined to describe objects
that are structured collections of related values (e.g., a
vector of Booleans, a table, or a complex number consisting of real and
imaginary components). Mesa's type system has other, perhaps less
obvious applications. These include expressing some of the
programmer's knowledge about a class of variables (e.g.,
that all take on values restricted to some known interval),
separating variables with different semantics into different classes so that
they cannot be confused (e.g., to avoid "comparing apples and
oranges"), and hiding implementation details of abstractions
(e.g., to prevent the user of a table-lookup package from depending upon the internal
organization of the table).
Programmer-created types have the same status as Mesa's
built-in types. They can be used to declare variables and to
construct further new types. In addition, values of most constructed types can
be operands of the fundamental operations (4-, =, #).
A new type identifier is declared using the
following syntax:
TypeDecla ration :: = idList
: TYPE = TypeSpecification
Each identifier in the idList is thereby declared
to name the type denoted by the TypeSpecification. If
this declaration form is compared to a normal declaration, i.e.,
Declaration = IdList : TypeSpecification Initialization
:
it can be seen that "TYPE.'
fills the role of a TypeSpecification, and "= TypeSpecification" plays
the role of Initialization.
In fact, the newly declared identifier has type "TYPE" and
a value (which must be constant, hence the "=") that is
a TypeSpecification.
Any
predefined Mesa type (section 2.7) is a valid TypeSpecification: thus the following
are valid type declarations:
SignedNumber: TYPE = INTEGER;
UnsignedNumber: TYPE = CARDINAL;
Truth Value: TYPE =
BOOLEAN:
Char: TYPE = CHARACTER;
These type identifiers are now
valid type specifications
and can be used to
declare variables:
j: SignedNumber, n: UnsignedNumber,
b:
Truth Value:
c:
Char;
After
this series of declarations, i and
j have
type SignedNumber, which
is equivalent to INTEGER:
n has
type UnsignedNumber, which
is equivalent to CARDINAL;
etc. This is a trivial way of defining
new types. A more interesting way uses a type constructor as
the TypeSpecification and generates a truly new type. not just an
additional name for an existing one. A TypeSpecification can
be defined as
TypeSpecification :: = PredefinedType
Typeldentifier
TypeConstructor
(TYPE
itself is not
a TypeSpecification: it can be used only to declare
types.)
There
is an important point worth emphasizing here. A TypeSpecification that is a PredefinedType
or a Typeldentifier denotes an existing type and yields
the same type every time it is used. A declaration such as the one of
SignedNumber introduces
a synonym for the name of an existing type. Synonyms can be more
descriptive and thus improve readability, but they do not partition the set of values.
The types SignedNumber and
INTEGER are
fully equivalent, and values with these types can be used
interchangably. On the other hand, a TypeConstructor constructs
a new type. The rules for equivalence and conformance of constructed types
depend upon the forms of their constructors and are discussed as
the constructors are introduced. In some cases, each appearance of a
constructor generates a unique type, i.e.. writing the same sequence of symbols
twice generates two distinct, incompatible types. For this reason, programmers
usually should name such a type, using a TypeDeclaration, and
thereafter use the type's identifier. Of course, introducing an
identifier for a constructed type can make a program easier to read and modify
in any case.
 described in chapter 2 (except for STRING in
chapter 6 and process related The simplest form of a Typeldentifier
is given by
described in chapter 2 (except for STRING in
chapter 6 and process related The simplest form of a Typeldentifier
is given by
= identifier I -- which is a declared type
• • • -- other forms
given in chapters 6 and 7
The
rest of this chapter discusses the attributes and uses of some common
constructed types: enumerations,
subranges, arrays, records, and
pointers. The
syntax for TypeConstructor is
 TypeConstructor
= EnumerationTC
TypeConstructor
= EnumerationTC
Sub
rangeTC A rrayTC
RecordTC PointerTC LongTC
Procedu reTC
A rrayDescriptorTC RelativeTC SignaITC
PortTC
ProcessTC
--
for enumerations -- for subranges
-- for arrays
-- for records
-- for pointers
--
for long
pointers, etc
-- see chapter 5 -- see
chapter 6 -- see chapter 6 -- see chapter 8 -- see
chapter 9 -- see chapter 10
(The suffix "TC" is to be understood as an
abbreviation for "TypeConstructor''.)
|
Enumerations
define a set of values by giving a list of identifiers members of an ordered set.
|
. These identifiers can be viewed as
|
Subranges define types with values drawn from those of a
larger, encompassing type but restricted to lie in a specified
interval. The subrange takes on the characteristics of the enclosing type: for example.
a subrange of INTEGER can
be used to declare
variables that behave as INTEGERS but are constrained to take values
within some interval.
Arrays arc sequences of components that arc homogeneous
with respect to type and are accessed by computed indices
("subscripting"). Records are sequences of components that have
potentially different types
and are accessed using fixed component names ("selection"). Records
and arrays are Mesa's aggregate data types.
Pointers arc scalar values used to access data objects
indirectly. A pointer value is represented by an address. Pointers
can be used to build linked lists, tree structures, etc. Long pointers are
pointers capable of spanning a larger address space than ordinary
pointers.
Chapter 3 concludes with a discussion of type determination. the
process by which Mesa decides whether an expression has an
acceptable type for a given operation. This is closely related to questions
of the equivalence and conformance of types.
3.1. The element types
This
section describes a class of types called element types. Their common properties are the following:
(1) They
are ordered types; values of an element type can be operands of all the
relational
operators (section 2.5.2).
(2) They
are scalar types;
a value with an element type does not have any visible or directly
accessible internal structure insofar as the language is
concerned.
(3) They
can be used to declare subrange types (section 3.1.2).
(4)
They are the only types allowed as index types
of arrays (section 3.2). The element types are INTEGER, CARDINAL, CHARACTER. BOOLEAN. the
types generated by
EnumerationTC, and
the types generated by SubrangeTC. Because of (3) above, this definition is
recursive; subranges of subranges are allowed. The definition of the class ElementType is
ElementType = INTEGER I CARDINAL I CHARACTER I BOOLEAN
EnumerationTC Sub rangeTC
A fine
point:
Note that LONG INTEGER and LONG
CARDINAL. althoueh ordered scalar types, are not element types. It is not possible to declare subranges
of these apes or to use lone numeric values as array indices.
3.1.1 Enumerated types
Consider the following declarations and a typical
assignment:
channel.S'tate: INTEGER;
disconnected:
INTEGER =
0;
busy: INTEGER = 1;
available:
INTEGER = 2;
channelS tale f-
busy:
Suppose channelState
is a variable that is intended to range over a set of
three "states" named disconnected,
busy, and available,
which are represented by values 0, 1, and 2. These values
have no real significance; 5, 6, and 7 would serve equally well.
Enumerated types are well suited to such an application (where
the underlying values are unimportant). The above declarations could be replaced
by a single declaration of a variable with an enumerated range:
channelState: {disconnected, busy, available}: channelState - busy:
The effect is the same as before: channelState is a variable with
values ranging over the same "states". and
similar assignment statements
can be used.
The enumeration has some advantages over the original
declarations:
It
is more convenient: the programmer does not have to provide values for disconnected, busy, and available.
It
allows more type checking. In the INTEGER case, one could assign any
short numeric value to channelState.
It helps documentation; an enumeration
shows all of its possible values.
An enumerated type is constructed by specifying a
list of identifiers between braces, "{...}". These identifiers
are not variables, but constants of that enumeration called identifier constants. They
represent nothing more than their own names.
The type constructor EnumerationTC
is defined
as follows: EnumerationTC =
{ IdList }
The IdList supplies all the identifier constants
for the enumeration, and duplication of identifiers is illegal.
Separately specified enumerations
are distinct. Every appearance of an EnumerationTC generates
a new type that is not equivalent to, and does not conform to. any other
enumeration. Thus the declarations
foreground: {red, orange, yellow,
green, blue, violet background: {red,
orange, yellow, green, blue,
violet
specify two different enumerations. It is illegal to assign background to foreground, despite the fact that
the same identifier list appears in each declaration. Occasionally, the
inability to declare any further variables with the same type can be used
to advantage by the programmer. Otherwise, the best way to avoid
such problems is first to declare a type and then to declare variables using
the identifier of that type; for example:
Color: TYPE = {red, orange, yellow, green. blue. violet foreground:
Color,
background: Color:
This
allows the assignment of background
to foreground as
well as the declaration of further variables with the same type
(perhaps initialized differently).
The identifier constants in two different enumerated
types have no association whatsoever and do not need to be
distinct from one another. To identify unambiguously the enumeration from which
a constant is taken, one can, and sometimes must, qualify' the
identifier constant by the name of the enumerated type. For example, eiven the
additional declaration
Fruit: TYPE = {orange. lemon};
Color[orange] denotes
a color and Fruit[orange] denotes
a fruit. More generally, the syntax used for this form of
qualification is
Primary = I Typeldentifier
[ identifier ]
(This
adds a new case to the syntactic definition of Primary,
which already allows an identifier constant.)
Often qualification is not necessary: for instance, the following is permitted:
hue:
Color;
hue orange: -- the
type of hue implies
Color[orange]
In the following situations, an identifier constant need not be qualified.
because the intended
enumerated type is established by the context:
as the RightSide of an assignment
as an initializing Expression
a component in an array or record constructor (sections
3.2.2 and 3.3.4)
--_-_ I as an argument of a procedure (chapter 5)
as an array index (section 3.2)
as
the right operand of a Relation, including that part of a Relation used
to label an arm in a discrimination (section 4.3)
as the bounds in a Su b rangeTC (section 3.1.2)
The values of an enumeration are ordered. The
ordering is given by the order of appearance in the IdList used to construct
the enumerated type. The leftmost identifier has the smallest value, and values
increase from left to right. The following relations all have the value TRUE:
Color[red] < Color[orange]
Color[red] < violet
hue IN [red .. -- assuming
hue = orange
There are two additional built-in functions that are applicable to
enumerations:
FIRST [TypeSpecification]
yields the smallest value of the specified enumeration;
e.g.,
FIRST [Coloij= red. Similarly, LAST [TypeSpecification] produces
the greatest value in an
enumeration;
e.g., LAST [Color],
violet. It
is also possible to iterate over all values of an enumeration
(section 4.5).
The predefined type BOOLEAN is really an enumerated
type, and its definition is
BOOLEAN: TYPE =
{FALSE, TRUE}:
Thus,
FALSE<TRUE, FIRST
[BOOLEAN] = FALSE, and LAST [BOOLEAN] = TRUE. Note, however, that
the BOOLEAN constants
TRUE and
FALSE may
always be used without qualification.
3.1.2. Subrange types
In many cases. the values of a variable are inherently
range-limited. For instance, a value for day (of the month) lies in the range [1..31]. In
other cases, the range is limited by design. For instance, a
value for year might
be limited to the range [1900..1999]. Mesa permits the user to declare such variables
in the following way:
day: CARDINAL [1 .. 31];
year: CARDINAL [1900 .. 1999];
Since these intervals cover a subrange of CARDINAL, the
variables day and
year are called
subrange variables. It is useful to think of day and year as having type CARDINAL with
the additional constraint that values are restricted to the specified intervals.
Subrange types have a
number of advantages and uses. Subrange declarations unambiguously document
the range of values intended for a variable and thus aid software maintenance.
The compiler is able to optimize storage allocation when
dealing with range-restricted variables (for example. in
arranging the fields of a record. section 3.3) and can take advantage of
subrange declarations to generate more efficient object code.
The
general form of a Su brangeTC is
Su brangeTC = Typeldentifier Interval I
Interval
The Typeldentifier must evaluate to an ElementType. Thus,
one can declare types that are
subranges
of INTEGER,
CARDINAL. CHARACTER, BOOLEAN, enumerated types, and other
subrange types. For example,
SymmetricRange: TYPE = INTEGER [—
PositiveInteger• TYPE =
CARDINAL [1..LAST [INTEGER]];
UpperCaseLetter: TYPE =
CHARACTER ['A..'Z];
DegenerciteTjpe: TYPE =
BOOLEAN [TRUE..TRUE]:
CoolC olor: TYPE = C oloityellow..LAsT
[Color]]: -- excludes
red orange, yellow
AthroughM: TYPE = UpperCaseLetter['
A..'M]; subrange
of a subrange
The
base type for
a subrange is that type of which it is a subrange and which is not itself a subrange;
e.g., the base type for both UpperCaseLetter
and Athroughill
is CHARACTER.
The Expressions
that define the end points of an interval must have types
that conform to the type denoted by the Typeldentifier (or yield short numeric
values if the identifier is omitted). Also, for the purpose of defining a subrange type, the
end points must be compile-time constants.
A fine point:
It is permissable for
the interval defining a subrange type to be empty. It is not legal
to use a variable of such a type. but an empty subrange is sometimes useful for
specifying the bounds of an array in a record declaration (section 3.2).
A subrange type conforms to its base type, and a base
type conforms to any of its subrange types. By extension, any two subrange
types with the same base types are mutually conforming (even if they
do not overlap in any way). A more revealing point of view is that the value of
a subrange variable has the base type as its type. and an assignment
of a value to a subrange variable makes an associated
assertion that the value is in the appropriate interval. A violation of such an
assertion is called a range error. It is the programmer's responsibility to guard against
range errors. As implied by this viewpoint,
appropriate literals of the base type serve as literals of the subrange type,
and any operations defined on the base type automatically extend to the
subrange type (but usually without closure).
Examples:
n: CARDINAL [0..10]; in: INTEGER
[— 5-5]:
in 0; n <- 0; -- inherited literals
n F n+1; --
not valid if n = 10
17 4"
in; -- only valid if m IN [0..5]
The preceding discussion implies that subrange
restrictions can be ignored in answering many type-related
questions; in this sense. subrange types are "weak." Two subrange
types are equivalent if their base types are equivalent and if the
corresponding bounds are equal. For these types, equivalence is much
stronger than conformance. Equivalence becomes important when subrange types
are used in the construction of other types.
FIRST
and LAST are applicable to all subrange types and yield the
corresponding bound. For example. FIRST [CoolColod=
green and LAST [Athroughill]='M. It
is also possible to iterate over all values in a subrange (section 4.5).
A
fine point:
The operators FIRST and
LAST are applicable to all element apes. including INTEGER. CARDINAL and
CHARACTER_ as well as LONG INTEGER and LONG CARDINAL. When applied to the
numeric apes. they supply
information about the range of ialues supported by a particular implementation.
3.1.2.1. Subranges of numeric types
*
The description above applies to subranges of both
enumerated and numeric types. Numeric subranges introduce one
further complication, which is the question of representation. Omission of the
initial Typeldentifier in a SubrangeTC
is permissable if and only if each bound in the Interval specifies a short numeric
value. In that case, INTEGER
or CARDINAL is the base type, and the
choice depends upon the representations of the bounds.
A numeric subrange type has
a signed representation if both bounds are elements of INTEGER and
at least one is not an element of INTEGER n
CARDINAL. Similarly, it has an unsigned representation if both
bounds are elements of CARDINAL and at least one is not an
element of INTEGER n CARDINAL. If
both bounds are elements of INTEGER n CARDINAL, values of that
subrange type are considered to have both representations. Any other combination of bounds is
illegal.
Examples:
sl : [— 10..10]; -- signed representation
s2: [100..33000]; -- unsigned representation (if 33000
> LAST [INTEGER])
s3:
[0..10); -- both representations
With respect to the choice of signed or unsigned versions
of arithmetic. and relational operators, a quantity with both representations
is treated flexibly. When combined with an unsigned value. it is considered
to be unsigned; the unsigned operation and result are chosen. When it is
combined with a signed value, the operation and result are
signed. The rules governing combinations of values with both
representations depend upon the context in which the result is used; the
default is to choose signed representation and INTEGER operations.
The precise rules are discussed in Section 3.6.
Examples:
i: INTEGER; n: CARDINAL; -- plus
the declarations above
|
(signed)
(unsigned)
|
sl + 1 sl + s3 s3— i
s2
+ 1
s2
+ s3
s3
* n
|
A
fine point:
The representation assumed for a
literal also depends upon context. In fact, any short numeric constant c is treated as if its type were [c..d.
Range assertions *
Assignment to a subrange variable implies an assertion
about the range of the expression being assigned. The programmer
may make such an assertion explicitly, for any expression, by using a range assertion. If S is an identifier of a
subrange type and e is
an expression with a type T conforming
to 5, the
Primary S[e] has the same value as e and is additionally an
assertion that e
IN [FIRST rsn LAsT[sn 7]] is TRUE. In
addition to user defined types, the basic types INTEGER
and CARDINAL may
be used in range
assertions.
.4 program that violates one of its range assertions is in error. In
addition to providing
documentation and (optional) run-time checking, a subrange
assertion affects the attributes attached
to an expression. For example, an assertion of an INTEGER range
(or a signed subrange) forces the result to be treated as a
value with signed representation. This is useful for controlling the choice of an
operation when the intended one cannot correctly be inferred from the operands
(section 3.6).
Examples:
1.- INTEGER; n: CARDINAL; S: TYPE = [0..10];
CARDINAL
[i] i is asserted to be
nonnegative
Sin] --
asserts n IN [0..10]
3.2. Arrays
Arrays are indexable collections of homogeneous
components. In other words, the components of a given array all
have the same type, and each corresponds to one index value in a range of
indices associated with that array. The range of indices (which is actually a
type called the index type) and
the component
type determine the array type. For example:
earningsPerQuarter: ARRAY [1..4]0F
INTEGER;
declares a variable with a constructed array type having
an index type of [1..4] and a component type of INTEGER. Thus,
earningsPerQuarter is
an array of four integer elements: earningsPerQuarter[1],
earningsPerQuarter[2], ,
earningsPerQuarter[4]. earningsPerQuarter by itself refers to
the entire array variable. (Aggregate variables and components of
aggregates are generally called "variables". If
a distinction is needed, the term component
is used and always means an item contained within an
aggregate.)
An index type must be an element type (other than INTEGER or
CARDINAL). A
one-to-one correspondence exists between the components of an array
and the values of the index type. This allows array elements to be
accessed via "indexed references". An indexed reference selects
and accesses the component corresponding to a particular index
value. In its simplest form, it consists of the name of an
array followed by a bracketed Expression
with a type conforming to the array's index
type.
An index type can be specified using a
type identifier:
Quarter: TYPE = [1..4];
profit,
loss, earnings: ARRAY Quarter OF INTEGER: thisQuarter: Quarter:
earnings [thisQuarter] 4- profit [thisQuarter] —
loss [thisQuarter];
The arrays profit,
loss, and earnings have
Quarter as
their index types, and thisQuarter is
a subrange variable with type Quarter.
Index types may
also be enumerations or subrangcs thereof. For example,
CallType: TYPE = {longDistance.
tiel.ine. toll, local, inPlant}: nearbyCalls: ARRAY CallType[toll..inPland OF CARDINAL:
nearbt•Calls[locall.-
nearbyCalls[local+ 1:
Components
may be of any desired type. In particular. the component type may itself be an
array type. This allows an approximation of multidimensional
arrays, which are otherwise absent in Mesa. For example, a
two-dimensional data structure can he declared and used as follows:
Matrix3by4; TYPE = ARRAY [1..3] OF ARRAY [1..41
OF
INTEGER:
mxy:
nog [3]
[4] 4- 0; -- clear last component.
In
the assignment statement, tnxy is
an expression of array type (with index type [1..3] and component
type ARRAY [1..4] OF
INTEGER). wxy[3] is
an indexed reference to the third component of mxy. This in turn yields an
expression of array type (with index type [1..4] and component type INTEGER). Thus,
nay [3] [4] is an indexed reference to the fourth component of that subarray. Because of
left-associativity, mxy [3] [4] is the same as (mxy [3]) [4].
An array
constructor consists of an optional type identifier followed
by a list of values (syntactically, Expressions)
enclosed in brackets. The list specifies values for
components of an array in index order. The declaration below
uses an array constructor to initialize an array that can be used as a translation
table: i.e., octalChar[n] holds the
character denoting octal digit n:
octalChar: ARRAY [0..7] OF
CHARACTER = ['0, '1, '2, '3, '4, '5, '6, '7];
Note that the number of values in the list (eight) matches
the number of indices in the index type. This is required for array constructors. A
special form using the replicator ALL is
available for abbreviating array constructors in which all
components have the same value. For example, the following two
declarations are equivalent:
dashes: ARRAY [0..7] OF CHARACTER 4- •-,
dashes: ARRAY [0..7] OF CHARACTER 4- ALL [.-]:
Array variables may also be
initialized using other array values. Consider the following example:
freshVector. ARRAY [0..3) OF CARDINAL = ALL [0]: current Vector: ARRAY [0..3) OF CARDINAL 4- fresh
Vector,
In this case, current
Vector is initialized with fresh Vector's value, i.e., all three of current Vectors elements are
initially set
to zero.
When the operands of any of the fundamental operations (4-,=.1t) are
arrays, the operation is applied on a component-by-component basis. The
initialization of current Vector above
uses assignment in this way. Similarly, the expression "current Vector = fresh Vector" yields
the result TRUE if
and only if all three components of each array are equal (as they are in the
above example). Because the declaration of fresh Vector uses fixed
initialization, assignment either to the entire array or
to one of its elements is illegal.
3.2.1. Dechwatiou of arrays
Arrays are declared using the array type constructor. A rrayTC:
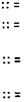 A rrayTC PackingOption
A rrayTC PackingOption
IndexType ComponentType
PackingOption ARRAY IndexType OF ComponentType
empty I -- elements
word aligned
PACKED --
elements potentially packed within words
ElementType Typeldentifier
TypeSpecification
Two array types are equivalent if both their index types
and their component types are equivalent and if they are both packed
or both unpacked (see below). An array type conforms to another if the two
types are equivalent. Thus it is possible to assign or compare array variables
with separately constructed types if those types are
structurally identical (see the assignment to currentVector
above).
A fine
point:
In additon. one array type freely
conforms to another if the component type of the first freely conforms to that of the second, the index types are
equivalent, and they are both packed or both unpacked (see section 3.5).
Declarations of initialized array variables take the form
IdList : ArrayTC
Initialization
The initializing expression must have an array type conforming to the one
being declared.
The previous section describes indexed references to array
components. A formal definition follows:
IndexedReference Variable
I Expression I I
( Expression ) I Expression
I
LeftSide IndexedReference
The Variable or
the parenthesized Expression must be of some array type, and the bracketed Expression must
conform to the index type for that array type. An IndexedReference is
itself part of the definition of a Leftside (and
therefore of a Variable, section 2.5).
Some
fine points:
Unless an array is
packed, each component is "aligned". i.e.. begins on a word boundary.
Currently, a byte is the smallest unit into which the elements are packed. Thus
a packed array of CHARACTER wastes no space. but a packed array of BOOLEAN has considerable
overhead.
Since packed array
elements are not necessarily word aligned. one cannot use the C
operator (section 3.4) to generate the address of
an clement.
The length
of an array is
the number of its elements. For variables with an array type. the length
is fixed and known at
compile-time. (Dynamic arrays are possible in Mesa through the use of array
descriptors, discussed in section 6.2.1.)
The IndexType of an array may legally be an empty
interval. In this case, no storm is allocated for the array. This is useful when the
array appears as the last component of a MACHINE DEPENDENT RECORD (section 3.3) and the user will be
obtaining storage for each record plus some number of array elements
from a free storage manager. Note that [0..0) is not equivalent to [1..1).
since the intervals specify different initial indices for the array.
Three function-like operators are
relevant to arrays (and more relevant to array descriptors): LENGTH. BASE, and DESCRIPTOR.
These are discussed in section 6.2. but a brief summary is provided below. For
this summary
. mg denotes an expression with
some array type.
LENGTH [arg] -- yields the number of array
elements.
BASE [arg] yields a pointer value for locating
the first array elemenL
DESCRIPTOR [arg] yields
argis array descriptor value (consisting of base
and length).



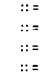 constructors are used only for initialization.
Actually, constructors RightSide context. An array
constructor is defined as follows:
constructors are used only for initialization.
Actually, constructors RightSide context. An array
constructor is defined as follows:
Constructor I ...
OptionalTypeld
[ ComponentList ] I ALL [ Component ] Typeldentifier I empty
PositionalComponentList
 -- other forms for record constructors
-- other forms for record constructors
=
Component
PositionalComponentList
, Component
=
empty I --
elided component
Expression I
NULL
The empty components in a constructor are said to be elided, and NULL components are said
to be voided. The
values of both elided and voided components are undefined. In the first form of
array constructor, the number of Expressions plus elided
or voided components must match the length implied by the
array type. The type of each Expression must conform to the array's
component type. The expressions (and elided or voided components)
are taken in order to form a sequence that is the constructed
array value.
Consider the following example:
Triple: TYPE = ARRAY [1..3]
OF CARDINAL;
triplet: Triple 4- Triple [11,
12, 13];
The declaration assigns 11 to triplet [1], 12 to triplet [2] and 13 to triplet [3].
When
the array type is implied by context, the Typeldentifier may be omitted
(see the discussion of record constructors, section 3.3.4). Thus
the declaration above could be written as
triplet: Triple 4- [11, 12, 13]:
Taken
out of context, the constructor [11, 12. 13] is ambiguous: it could be assigned
to any array
of three numeric elements: for example:
trio: ARRAY {Patt}, Laverne. Maxine} OF LONG INTEGER +- [11, 12, 13];
The second form of constructor, using ALL, is
only valid
when the array type is implied by context. The type of the Expression
must conform to the array's component type. The value of the constructor
is an array in which the specified value is replicated a number of times equal
to the length of the array. The expression is evaluated just
once. In the case of an array of arrays, the structure must be
mirrored by nesting in the constructor, as shown by the following example:
allOnes: Alatrix3by4 4-
ALL [ALL [1]]:
Some
fine points:
The value of an elided or voided
component of an array constructor is not defined, but it will have some value.
In
particular. if the statement
triplet +- [1. , 3]:
is
executed after the previous assignment to triplet. the value of triplet [2] is undefined.
Any array constructor
in which all components are compile-time constants is a compile-time constant_
Also, selection from
an array that is a compile-time constant using a constant index yields a
compile-time constant.
3.3. Records
A record
is an aggregate that allows a group of related data items
of different types to be packaged together. In the definition
of a record type, the type of each individual component must be supplied.
as in the following example:
MilitaryTime: TYPE = RECORD [hrs: [0..24). [0..60)1:
oldTime. newTime:
Here„IlditwyTime is a newly defined type, and oldTime and neit•ime are
record variables of that type. IlilitaryTime is a two-component record type, where the first
record component is named hrs and
the second rains. Every AlilitaryTime
record contains both components, but different record objects
have their own values for these components.
A constructor of a record type contains a field list after the word RECORD. Each
element in the list specifies one (or more) components of the record.
For Militaryrime, the field list is [hrs:
[0..24), mins: [0..604
The component names, hrs and
rains, are
called field names. They
are used to refer to components in any Illilitar•Time record.
For instance, the first component of oldTime may be selected using the qualified reference, "oldTime.hrs".
One can construct an entire record value using a record constructor. For
instance, the constructors below yield MilitafryTime values with hrs components that have the value 13 and mins components that
have the value of the expression "y+1":
AfilitaryTime[13, y+ 1] AlilitagTime[hrs: 13,
mins: y+
1]
The
second constructor is an example of a keyword constructor, since it specifies the name
of the component (e.g., as "hrs:") with which a value
is to be associated.
A default value can be specified for any field in the
definition of a record type. The default is used in constructing records of
that type when no value is specified in the constructor. Defaults are useful
for suppressing detail and ensuring initialization of fields. In the following
example, the two constructors have the same value:
Datum: TYPE = RECORD
value: INTEGER, nReads: CARDINAL nWrites: CARDINAL 1:
Datum [x]
Datum [value:
x, nReads: 0, nWrites: 1]
The basic operations on (non-variant) record
values include the fundamental operations (=, #, 4-), as
well as qualification and
extraction for accessing the
record's components.
3.3.1. Field
lists
There are two kinds of field lists, depending on whether
the fields are "named" or "unnamed". (Field
lists used to construct multi-component
record types are almost always named).
Syntax equations:
FieldList = [
UnnamedFieldList [ NamedFieldList
UnnamedFieldList = TypeSpecification
TypeSpecification UnnamedFieldList
 NamedFieldList
NamedFieldList
FieldDescription
DefaultOption
Examples:
[i:
INTEGER, b: BOOLEAN, c: CHARACTER] [INTEGER. BOOLEAN,
CHARACTER]
[17:
CHARACTER, f2.
f3: INTEGER]
[fl: CHARACTER, f2: INTEGER. fl:
INTEGER]
a named field
list
a similar, but unnamed field list components listed and
declared together equivalent to the above
Note that if one field is named, all must be named.
Also, field names must be unique within a given field list. (The same
identifiers may be used as field names in other field lists, however, or as names
of declared variables.)
Field
descriptions in a named field list contain a type specification, indicating the
type of the field. Any type may be specified, including an array
type or (some other) record type.
Some
fine points:
A field's type specification must not
imply an infinite nesting of records. For instance, the following is illegal:
A:
TYPE = RECORD
[b: B]:
B:
TYPE = RECORD
[a: A]:
Field lists occur in
constructors of types other than records, such as PROCEDUREs (chapter 5).
SIGNALs (chapter 8).
and in variant record
specifications (chapter 6).
Unnamed field lists are
normally used when component names would be ignored if they were present. This
is common for
functions that return single-component results. "Unnamed field lists are
sometimes used in specifying
the input parameters for procedure variables that are to be set to one of
several actual procedures. (However, an unnamed field list does not allow Calls using such a
procedure variable to refer to the parameters by name.)
3.3.2. Declaration of
records
The type constructor RecordTC is defined as
follows:
RecordTC = RECORD FieldList
-- plus variant records
(chapter 6)
where FieldList is
defined in the previous section. Separately declared record types are unique, even
if they look the same. Every
appearance of a record constructor creates a new type that is not
equivalent to, and does not conform to, any other record type. In
the example:
ReCT-Jpei:
TYPE RECORD [a,b: INTEGER];
reel: RecTypel;
RecType2: TYPE RECORD [a,b: INTEGER]:
rec2:
RecType2;
rec3:
RECORD [a,b: INTEGER];
rec4: RECORD [a,b: INTEGER];
the record variables reel, rec2, rec3, and
rec4 all have different, non-conforming types. None of these
can be assigned to any of the others (despite the similarity of their components).
It is, of course, legal to
assign to a component any value with a conforming type. For example:
recl.a rec2.b rec3.a 5:
rec4.a recl.a; rec4.b recl.b;
Any single-component record type conforms to the
type of its single component, but not vice versa. The
automatic conversion
in this case requires no computation.
Example:
Bundle: TYPE = RECORD [value:
INTEGER]:
recEar: Bundle;
iniVar: INTEGER;
intVar 4-
recVar; --
means intVar 4-- recVar.value
intVar recVar+1; --
operand conversion
recVar F Bundle[intVat]; --
a constructor
recVar.value intVar,
This
conversion simplifies dealing with functions that return single-component
records (chapter 5). It also provides a way of partitioning a set of
variables that can be checked by the type system. In the
example above, a direct assignment of intVar to recVar
is invalid. Furthermore, no other single-component
record type, such as
Prime: TYPE = RECORD [value:
INTEGER];
can be confused with Bundle; assignment of a Bundle value to a Prime, or a Prime to a Bundle, is illegal.
Either a Bundle or
a Prime can,
however, appear as a numeric operand. Defining Bundle and Prime as synonyms for INTEGER would
not provide this additional checking.
Because of the uniqueness of constructed record
types, record variables are typically declared in two steps: first the record type, then the record variables. The general form is:
identifier : TYPE = RecordTC ; --
define record type.
IdList : identifier Initialization ; -- same identifier
as just defined
Record variables can also be declared directly:
IdList : RecordTC Initialization ;
This form is not
very useful because the (unnamable) record type is not available for purposes
such as declaring other records of the same type or writing
constructors.
The Initialization shown in these general forms
applies to the entire record variable, not to individual
components. Any Initialization must have the
proper record type. Initialization
of
record variables
is shown in the next example.
noon: AfilitatyTime = [hrs:12,
mins:0];
midnight: AfilitatyTime = [hrs:0,
mins:0];
time: AlilitaryTime 4- midnight; --
start time at
midnight.
Some
fine points:
The Mesa compiler
packs record components into machine words The components may be arranged in an
order that differs
from the left-to-right order of the fields in the type constructor. All records
of the same type have
the same component arrangement.
Norman.. the user
is unconcerned with the actual arrangement of record components. When component
arrangement is
important, the user may specify
"MACHINE DEPENDENT" records. An
example is:
InterruptWord: TYPE =
MACHINE DEPENDENT RECORD
device:
DeviceNumber,
channel: [0..7].
stopCode: {finishedOk. errorStop. powerOffl, command:
ChannelCommand
In this case. the user
takes full responsibility for component arrangement. Components are positioned
exactly as green.
from left to right in machine words. In general. "fill" components
are needed to ensure that no field crosses a word boundary (unless it starts on one).
Components (such as ChannelCommand) may themselves be aggregates occupying more than one
word
It
is also the user's responsibility to "fill out the record to a
full word if the record crosses a word boundar3. (Interrupt Word might be correct for a 16-bit
machine. but not for a machine having a larger word length).
Except
in MACHINE DEPENDENT records. components are packed for storaee efficiency.
Some fields ma} be aligned
(to the beginning of a word boundary) and some may not. Components occupying a
full word or more are
always aligned: arrays. INTEGERs
and pointers. for example. Subrecords may or may not be
aliened.
depending on their size. Packed arrays are always aliened.
even if there would have been space in the
preceding word for a b3te-sized
element.
The
function-like operator SIZE is often used to find the number of machine words
occupied by a record of some type. The general form is: SIZE [TypeSpecification]. The result is a
CARDINAL value. the number of words required by an object with the type specified by the argument.
SIZE may be used to find the number of words required for any type
of object.
3.3.3. Qualified references
Qualification is used to refer unambiguously to a named
component of some record. The general form (which extends the definition of a LeftSide) is
QualifiedReference = Variable . identifier I
( Expression ). identifier
LeftSide = I
QualifiedReference
The field name is said co be ''qualified by" the
record value (the Variable or
Expression) to the left
of the dot. The operator associates from left-to-right in the case of multiple
qualification. For example:
Latitude: TYPE = RECORD [degs:
[0..360), mins, secs: [0..60)];
Longitude: TYPE = RECORD [degs: I— 90..90], mins,
secs: [O..60)]:
Position: TYPE = RECORD [latitude: Latitude, longitude:
Longitude]:
somePosition: Position;
Some of the possible qualified references to components
of somePosition are
listed below:
Qualified Reference Refers
To
somePosition.latitude 1st
sub-record
somePosition.longitude 2nd
sub-record
sornePosition.latitude.degs 1st component of
1st sub-record
somePosition.longitude.secs 3rd
component of 2nd sub-record
The
association order for qualification means that names must occur in the proper
sequence: e.g.. somePositiolunins.longitude
is incorrect. Also, a qualified reference must be
complete, i.e., names may not be skipped (as in somePosition.secs, which
would be ambiguous in any event).
Qualified references and indexed references have the same
precedence (the highest possible) and may be intermixed. For
example:
recordOfArrays: RECORD [a.b: ARRAY
[0..100) OF CARDINAL];
arravOfRecords: ARRAY [1..5] OF RECORD CARDINAL];
• • •
array0fRecords[5].i3 record0fArrays.a[0]; -- ("last"
gets "first")
|
A fine point:
Qualification briefly opens up a
given "name scope". For instance. in the record qualification, qualified name. x. must name a
field of rec and selects that field_ Scope is
treated more fully in
|
rec.x. the chapter 7.
|
3.3.4. Record coirstnictors
A record constructor assembles a record value
from a set of component values. In the following example.
a constructor is used
as a RightSide of an assignment.
Month:Vow: TYPE = {Jan, Feb. Mar, Apr. .11 ay. Jun..lul. Aug, .Sep. Oct. Nov. Dec}: Date: TYPE = RECORD
day: [1 .. 31].
month:
MonthName, year: [1900 .. 2000)
birth
Day: Date:
dd: [1..31]: mm: MonthName: Sy:
[1900..2000); now: [1900..2000)
1976: birthDay r Date[25,
Apr, now— 33];
This constructor yields a record value with type Date. The record assigned to birthDay contains the following
component values:
Component Value
day 25
month Apr
yearnow-33 (which
is 1943)
A Constructor is a Primary and may not be
used as the LeftSide of an assignment.
Record constructors are
of two kinds: keyword constructors and
positional constructors. Within
both kinds, the component value for a particular field may
either be supplied or be omitted. If it is omitted, the value
of the field is determined by the DefaultOption appearing in the declaration of
the
field (section 3.3.5).


 ... I Constructor
... I Constructor
OptionalTypeld [ ConnponentList Typeldentifier I empty
KeywordComponentList I
PositionalComponentList
KeywordComponentList = KeywordComponent
KeywordComponentList
KeywordComponent
PositionalComponentList = Component
I
PositionalComponentList , Component
KeywordComponent = identifier : Component
Component empty
I -- elided component
Expression I -- explicit component
NULL -- voided component
The
initial Typeldentifier, if
present, must name the type of the record being constructed.
In keyword
constructors, the correspondence between constructor
components and record components is strictly "by name".
Keyword names may not be repeated
in a constructor, but the order is irrelevant. For example. the following keyword
constructors are equivalent:
Date[day: 25, month: Apr, year now— 33] Date[month: Apr,
day: 25,
year: now— 33]
All of these keyword constructors specify values for all
the components. In the following example. the first keyword
constructor elides the
month component
(the place for the component value is specified, but no value is
given): the second voids the
117011111 component
(by specifying NULL instead
of a value):
 Date[da•:
25. month:,
rear: now— 33]
Date[da•:
25. month:,
rear: now— 33]
25, month: NULL. }•ear: now— 331
The
distinction between an elided and a voided a field arises in the treatment of
defaults (section 3.3.5). Since the declaration of Date specifies no default value
fir month, both
of these examples construct records with a second component having
an undefined value.
In a positional
constructor, the correspondence between constructor
components and record components is strictly "by position".
The first constructor component corresponds to the first record component,
the second value to the second component. etc. Positional constructors may be
used for both records and arrays (section 3.2.2). It does not
matter whether or not fields are named in the
definition of the record type. The following three constructors are
equivalent:
Date[day: 25, month: „rear: now— 33] --
value of month is
undefined
Date[25„ now-33] --
value of 2nd component is undefined (elided)
Date[25, NULL. now— 33] --
value of 2nd component is undefined (voided)
Positional
constructors may elide or void components as shown above. but components not
supplied at the end of the list must be elided by supplying a
sufficient number of trailing commas.
Keyword and positional 1101111i011.5 may not be mixed in a single constructor. The
order of evaluation of components is not specified for either kind
of constructor.
The initial Typeldentifier in a constructor
may be omitted when the constructor is used as: the RightSide of an assignment
(unless the LeftSide
is an extractor, section 3.3.5) an
expression in an Initialization
a component of an enclosing record or array constructor
an areument of a procedure
the right operand of a Relation.
In
other cases, an initial Typeldentifier must
appear. It is never incorrect to supply the identifier, and
sometimes doing so improves readability.
A
fine point:
Any record constructor
in which all components are compile-time constants is a compile-time constant.
Also, a field selected
from a record that is a compile-time
constant is itself a compile-time constant
3.3.5. Default field values
The definition of a record type may specify a default
value for each field. These default specifications are optional;
if present, they are used in constructing records of that type when no values
for the corresponding fields are specified in constructors. An elided field, as
discussed in the preceding section, supplies no value. Specifying
some default treatment of a field also allows complete omission of that field in a
constructor. In a keyword constructor, a field is omitted by omitting
the keyword entirely: in a positional constructor. trailing fields (only) can
be omitted by omitting the final commas. The positional
constructor "[ ]" is considered to omit, not elide, its first component
(if any).
|
In the following example, all constructors
have Interval: TYPE = RECORD
range:
INTEGER.
origin: INTEGER *- 0.
direction: {up. down} r up
Interval[range:
10. origin: 0. direction: up] Interval[range: 10. origin:. direction: ]
Interval[range: 10]
nterval[10]
|
the same nalue.
all fields specified
origin. direction elided
origin. direction omitted
origin. direction omitted (positional form)
|


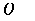 The
syntax for specifying defaults in a NamedFieldList follows: DefaultOption = empty I DefaultSpecification
The
syntax for specifying defaults in a NamedFieldList follows: DefaultOption = empty I DefaultSpecification
DefaultSpecification = empty I
Expression
I
NULL
Expression I NULL
Note: In the final line, the vertical bar denotes itself
and is embedded within an alternative.
Only
named fields may have default values. In a DefaultSpecification, the Expression must
have a type that conforms to the type
of the corresponding field.
Suppose that R is a record type with a
field v of type T. The
above syntax allows five forms for the DefaultOption in the
declaration of v. No matter which form is used, a constructor of an R may
explicitly specify a value for the field v. The various
options control whether the existence of the field must be made
evident in the constructor, whether an explicit value must be supplied and. if not_
what action is taken. The options are interpreted as follows:
(1)
v: T
In a constructor, the value of v can be left
undefined, but that must be indicated explicitly, by eliding or voiding the field. This Wile also applies to
an unnamed field.
(2)
v: T
Every constructor must supply
an explicit value (not
NULL) for
v.
(3)
v: T t e
If
a constructor elides or omits v. the value of the expression e is
used: voiding the field is not permitted.
(4)
T <- NULL
As
in (1) above. except that the constructor may omit v entirely. If the field is
omitted, elided or voided, its value is undefined.
(5) v: T F e I NULL
As in (4) above, except that a constructor may
explicitly void v. If the field is omitted or elided. the value
of e is
used: if it is voided. its value is undefined.
If the first or second form is used, the field cannot be
omitted from a constructor: these forms are useful when such omission is likely
to indicate a programming
error. Omission is permitted by the other forms, which differ in the default
action for an omitted or elided field. These forms are appropriate
when a field has some common and meaningful
default value (the third and fifth cases) or. alternatively, is
relevant only in unusual circumstances (the fourth case). The last three forms
are particularly suitable for extending the definition of a
record type: constructors in existing programs need not be
modified.
I-a,:3-
Chapter 3: Common
Constructed Data Types
Fine
points:
The
second form of field declaration guarantees that the field r has a well-defined
value in am record created 1)i a constructor (but not
otherwise).
if
ihe Expression form of a default specification is used. that expression is
evaluated at the time of construction but in the context of the declaration of the record. i.e..
the expression is treated as a parameterless procedure invoked e\
aluation of the constructor (see chapter 5).
The
default value of a field cannot be specified in terms of other fields in the
same record. Default values for fields of record types defined
in DEFINITIONS modules (section 7.3.2) must be compile-time constants.
|
Examples:
R: TYPE = RECORD
I:
CARDINAL,
v2: CARDINAL -,
v3: CARDINAL 4- 3,
v4: CARDINAL 4- NULL, CARDINAL 4- 5 I NULL
-- the following, are valid R[v1:
1. v2:
2]
R[v1: . v2: 2, v5:]
R[vl: 1, v2: 2, v5: NULL]
-- the following are not valid R[]
R[v1: 1, v2: NULL,
v3: NULL]
|
-- means R[v/: 1, v2: 2, v3: 3, thi: NULL. v.5: 5] -- means R[v , v2: 2, v3: 3, v4: NULL, v5: 5]
-- means R[v1:
1, v2: 2, v3: 3, v4: NULL, v5: NULL]
-- neither vl
nor v2 may be omitted -- neither v2 nor v3
may be voided
|
3.3.6. Extractors
Extractors are used to "explode" record objects
and assign their components to individual variables in
a single statement. For
example, the extractor below assigns the components of birthDay (defined
in the previous
section) to the variables
dd, mm, and
yy, in that order:
[dd, mm, yy] birthDay:
This
has the same effect as the following three separate assignments, except that birthDay is evaluated only once:
dd birthDay.day:
mm birthDayanotah; yy birthDay.year
An extractor resembles a constructor in form. but
there are some
important differences:
An extractor may only be used as a LeftSide, never as an Expression.
The "components" of an extractor specify LeftSides,
not Expressions. Extractors always begin
with a left bracket, never with a Typeldentifier.
The type of the record value assigned to an extractor must
be known to the compiler. This means that the following (rather
useless) statement is invalid because the constructor's type cannot be determined:
[dd, mm, yy] [25, Apr, 1943]: -- invalid
The statement
should specify the type of the constructed value: [dd, mm, YY] 4- Date[25,
Apr, 194.3]: --
valid
Extractors,
like constructors. may use keywords. This allows an extractor to he written
without regard to the record's component order. For instance, the following
statements are equivalent to the
first
one in this section:
[day: dd, month: mm. year: yv] birthDay: [month: mm, day: dd. year: n'] birthDay:
Extractors
may elide or omit any item.
in vnhich
case the corresponding record component is not assigned. The extractors shown
below arc equivalent:
|
[day: dd. month: , year: jy]
F birthDay: [day: dd, year: yy]
4- birthDay;
[dd. • yy] 4- birthDay:
|
-- month elided
-- month omitted
-- 2nd component elided
|
A
positional extractor may omit trailing components without supplying trailing, commas. The year component of birthDay is omitted below.
[dd, mm] birth Day:
An extraction operation (unlike an ordinary
assignment) yields no value. This
means that an extractor may not be
embedded within an expression. For example, the first
statement following is illegal: the
second is a valid
alternative:
r [x. y,
4 44. s; --
invalid
[x, y, 4 r s: --
valid
Syntax equations:
AssignmentStmt = I Extractor 4- RightSide
Extractor = KeywordExtractList I
[ PositionalExtractList
KeywordExtractList = KeywordExtract
KeywordExtract, KeywordExtractList
KeywordExtract •• - identifier : Extractltem
PositionalExtractList = ExtractItem I
Extractitem PositionalExtractList
Extractitem empty I -- component is ignored
LeftSide -- component is assigned
to LeftSide
The identifiers in a KeywordExtractList must be field
names for the record type. Note that an extraction list can be
empty, in which case the effect is to discard a record value. Extractors cannot be nested.
3.4. Pointers
Pointers allow efficient indirect access to objects. A
pointer may refer to only one specific type of item. For instance, the following pointer provides access only to
objects of type INTEGER:
intPtr: POINTER TO
INTEGER:
Another pointer might be specified to point only to BOOLEAN objects:
boolPtr: POINTER TO BOOLEAN:
These are different types of pointers since they
have different reference types, INTEGER and
BOOLEAN. Furthermore,
since INTEGER and
BOOLEAN are
incompatible types. these pointer types are also incompatible; i.e., assignment
of boolPtr to
intPtr, or
vice versa, is disallowed.
A pointer value-is represented by the
address of some data object. This object is called the pointer's referent. The postfix
operator T may be applied to a pointer value of any type to yield that value's referent. The process of "following" a pointer to its referent is
called dereferencing.
A dereferenced pointer designates a variable.
When the pointer is declared as above, the variable can be used as a LeftSide or as a Primary. Thus iniPtrr and boolPtrt are variables of type INTEGER and BOOLEAN respecti% ely. 'the statement
60011'1,1 (inthrt
= 0):
is executed by following iniPir to obtain a INTEGER value,
testing that value, and assigning the result to the BOOLEAN variable referenced by boolPir.
Sometimes a pointer is created simply to
identify an object or to allow indirect access to a value that is
not to be modified. Mesa provides readonly
pointers for such applications. A value with a readonly
pointer type cannot be used to update its referent. For
example, the declaration
ROiniPtr: POINTER TO READONLY INTEGER:
declares a readonly pointer. ROintPirt is a Primary with type INTEGER but
not a valid LeftSide.
Any type specification is permitted as the reference type
of a pointer type. The pointers declared below reference a named
record type.
Person: TYPE = RECORD
age: [0..200],
sex: {male, female},
party:
{Democratic, Republican}
1:
candidate!, candidate2:
Person:
winner, loser:
POINTER TO Person;
Pointers
to record objects may be used to qualify field names. if record candidate] is the referent of winner, then qualifications such as
wirnter:age winner.
sex winnerparty
select the corresponding components of candidate'. However, if candidate2 were the referent,
these same qualifications would select components of candidate2. When applied to a
pointer, the operation of selection implies dereferencing. For
example, winner.age specifies
dereferencing winner to
obtain a record variable of type Person
and then performing normal field selection on that record.
Thus winner.age
is an abbreviation of winnert.age.
It is common to define a record type containing
components that are pointers referencing objects with the same record type. For example, the type declared as follows:
Familyifember. TYPE = RECORD
someone: Person,
mother, father. POINTER TO FamilyMember
1:
might be used to create a tree of related persons in which
the relations are expressed directly by pointer linkages.
The fundamental operations (=. #, 4-)
applied to pointer values deal.with the pointers
themselves. not with their referents. In
the examples:
 winner 4-
loser:
winner 4-
loser:
winnert loserr:
first sets winner to point to the same Person as loser: the second assigns the
referent of loser to
referent of winner,
and thus has a quite different effect. The full set of
relational operators can applied to pointerS declared to be ordered; for
example:
orderedPtr: ORDERED POINTER TO Person:
The
ordering is determined by the memory addresses that represent the pointers. not
by the properties of the referents. Pointers
not declared to be ordered can be only be compared using the
operators = and #.
There is one pointer literal, NIL. It
conforms to any unordered
pointer type and denotes a pointer value that has no valid
referent. For
example:
IF iniPir = NIL THEN boolPtr 4- NIL;
A pointer with value NIL should
not be dereferenced; the result is undefined.
Pointer values are most commonly obtained from
allocators that provide and manage storage for a class of objects. The unary
prefix operator C.r. also generates pointers. When applied to a variable with
type T, it
yields a pointer to that variable with type POINTER TO T; for example:
winner 4- @candidate];
Pointer generation should be done with caution:
it is possible for the resulting pointer to outlive the referenced
object. A non-NIL pointer value with no valid referent is said to be a dangling reference. The
language does not prevent dereferencing such a pointer, but doing so produces
an undefined result. It is the user's responsibility to avoid
dereferencing a dangling (or uninitialized) reference.
3.4.1. Constructing pointer types
The type constructor
for pointers is defined
as follows:
PointerTC =
Ordered Base POINTER TO ReadOnly
TypeSpecification I
Ordered Base POINTER Interval TO ReadOnly
TypeSpecification
Ordered ::= empty I ORDERED
Base ::=
empty I BASE
ReadOnly = empty I READONLY
The TypeSpecification in a PointerTC specifies the
reference type of the pointer type. Two pointer types are equivalent
if their reference types are equivalent and if their attributes ReadOnly and
Ordered are specified identically. Thus equivalent pointer types can be
constructed in separate places, but they must have the same structure. One
pointer type conforms to another if the two reference types are equivalent, if
either the ReadOnly attributes are identical or the second is READONLY and
the first is not, and if either the Ordered attributes are identical or
the first is ORDERED and
the second is not. The Base attribute is ignored in determining conformance.
In the following examples, the first type in each pair
conforms to the second, but the second does not conform to the first:
POINTER
TO FamilyMember POINTER TO
READONLY FamilyMember
ORDERED
POINTER TO Person POINTER TO Person
ORDERED
POINTER TO Date POINTER TO
READONLY Date
Fine
points:
If one pointer type
conforms to another. it conforms freely (section 3.5.3). Conformance of pointer
types is extended by
the following rule: one pointer type conforms freely to another if the second
is READONLY. the reference
type of the first conforms freely- to the reference type of the second. and the
Ordered attributes
satisfy the restriction above.
The
second form of PointerTC constructs a subrange of a pointer ty-pe. Subranges of
pointers have the usual properties of subranues: e.g.. a pointer subrange type and its base type
mutually conform (hut not freely ). The values of a subrange pointer are restricted to the given
interval (and can potentially- be stored in smaller fields). Subranue pointer types are not
recommended for ueneral use. They arc intended primarily
for constructing relative pointer types (section 6.3)
which. unlike the subrange types. do not allow dereferencing without
relocation.
The attribute BASE
specifies that values with that pointer type are to be used as base values for
relocating relative
pointers (section 6.3). Such
values may also be used as ordinary pointers.
3.4.2. Pointer
operations
The general form of an indirect reference is:
IndirectReference =
Variable
( Expression ) T
LeftSide = I IndirectReference
The postfix operator T performs explicit dereferencing of the pointer expression
it follows. Its precedence is the same as indexing and
qualification (the highest possible), and these operations can be
intermixed. For example:
group: ARRAY [0..10) OF
POINTER TO FamilyMember,
group[i]tinothert
someone W(group[i])?),mother)t).someone
If
p is
an arbitrary pointer expression, then pt can
be read as "p's referent" or "referent of p". Application of the T operator produces a variable that may be used as
a Primary. Unless p is
a readonly pointer. pt (or any of its components) may also
be used as a LeftSide. The definition of conformance implies that an
ordinary pointer can be assigned to a readonly pointer, but not vice versa.
Thus the referent of a readonly pointer is not necessarily immutable: i.e., its
value might change during the lifetime of the readonly pointer. The
Mesa language only prevents updates of the object through
those pointers to it that are declared to be readonly.
The
syntax used for address generation is Primary = I LeftSide
The prefix operator @. produces the address of its
operand. If x is
a variable of type T. the
value of @x is a pointer to x, and its type is POINTER TO T.
@.x can be read as "address of x". The operand for @.
must be a valid LeftSide (it
cannot be a constant or an arbitrary expression, for instance).
The operator's precedence is lower than that of T: e.g., @xt is equivalent to
@.(xt) (or simply x).
Some
fine points:
There
are variables that cannot be the referents of pointers and thus cannot be the
operands of C. These include
all "variables" with fixed initialization and components of such
variables. In addition, a pointer value is represented by a word address. Therefore. a referent must
lie on a word boundary: an object having this property is called aligned. Variables are aligned except in
the following cases:
Elements
of packed arrays are not aligned.
Any component of a record that
occupies less than a single word is not aliened (but arrays, even if packed. are always aligned).
Care
must be taken so that a pointer to a declared variable does not exist longer than the
variable to which it points. Consider the following example (which
assumes familiarity with procedures. local variables and global
variables):
pointer!.
pointer2: POINTER TO INTEGER: -- two global xariables
RiskyProf: PROCEDURE [i: INTEGER] = i is a local variable
BEGIN
local:
INTEGER: -- and so is local
. .
pointer! -- risky: i will disappear upon RETURN
pointer2 @ local: -- also risky

 -- the "risky" pointers are valid up to this point. but -- NOT after this statement is
executed.
-- the "risky" pointers are valid up to this point. but -- NOT after this statement is
executed.
Pointers that are declared to be ORDERED may
be used as operands of all the relational operators (section 2.5.1). For this
purpose, they behave as unsigned numeric
values. The definition of conformance implies that an ordered pointer can be
assigned to an unordered pointer variable, but not vice versa. NIL iS not a valid ordered pointer
constant, and the relation of its value to other pointer values is
undefined. Also, the a operator
always produces an unordered pointer value.
The
following fine points cover pointer capabilities that should be used with
caution (and avoided when possible). Some of these capabilities
circumvent normal type-checking, and may result in unpredictable results if
used.
The
type POINTER TO UNSPECIFIED (or simply POINTER) can access actual data of any
type. Pointers of this
type conform to any other
pointer type. and vice-versa.
Limited arithmetic can
be performed on pointers. but programmers are encouraeed to use BASE and
RELATIVE pointers (chapter 6) if the purpose of the arithmetic is simple
relocation. A short numeric value added to. or subtracted from. a pointer produces another pointer
with the same type. Also, the difference of two pointer values with equivalent types is a CARDINAL.
3,4.3. Long Pointers *
Long pointers provide indirect access to objects
having memory addresses that cannot be
represented within a single machine word. Like LONG INTEGERS. they
are essentially concessions to
the limitations of hardware. Again, the
long variant provides somewhat greater generality at
somewhat greater cost.
Long pointer types are constructed as follows: LongTC
:: = LONG
TypeSpecification
The type constructor LONG can be applied to INTEGER (chapter
2), any pointer type, or any array descriptor type. (chapter 6). No
other type can be lengthened.
Long pointers are typically created by lengthening (short)
pointers as described below. In particular, NIL is automatically
lengthened to provide a null long pointer when required by context. The
standard operations on pointers (dereferencing, assignment, testing equality,
comparing ordered pointers) all extend to long pointers.
Both automatic and explicit lengthening (using the
operator LONG) are
provided for pointer types, and the type POINTER TO T conforms
to (but is not equivalent to) the type LONG POINTER TO T. Lengthening an expression
with the first of these types produces a value with the second: i.e., the
reference type and the Base. Ordered and ReadOnly attributes are
unchanged.
The operator (a. applied to
a nariable
of type T produces
a pointer
of type LONG POINTER
TO T if
the access path to that Nariable itself involves a long pointer and
of type POINTER TO T otherwise.
Some line points:
Two
conforming pointer t)pcs conform frecI only if both are long pointers or both
arc not.
NIL is lengthened in a
standard wa) and has a universal representation. All other pointers are
lengthened in a hardware
dependent ))a). There is no normalisation prior to operations on lone pointers.
and such pointers constructed
other than b) len;;thenina ma) i2i)e anomolous results (c.a.. in comparisons).
|
If either operand in
a pointer addition or
Examples:
R: TYPE = RECORD [fi T, ...]: p, q: POINTER TO R:
pp, qq: LONG POINTER TO R: pT: POINTER TO T:
ppT: LONG POINTER TO T:
-- the following are valid.
pp 4- qq; pp 4- N I L pp 4- p;
pp = qq, pp = NIL, pp
= q:
PT
4- C1P-f, PPT CPPf,
PPT
-- the following are not valid.
PP = PPT:
P
PP: PT
|
subtraction is long. all operands
are lengthened and the result is lone.
-- long comparisons -- pointer
lengthened
-- incompatible types
-- no automatic shortening
|
3.4.4. Automatic dereferencing
Automatic
dereferencing converts a pointer RightSide of type POINTER TO T into one of type T if that
RightSide is followed by dot qualification (section 3.3.3), a bracketed array
index, or a bracketed argument list (the last two are syntactically
identical). For example. in the following two statements. the
LeftSides are equivalent:
winner.party 4- Democratic:
win nert .party Republican;
Automatic multilevel dereferencing is possible.
Given the following declarations, the three final assignment
statements have the
same effect:
actualArray: ARRAY [0..20) OF
INTEGER:
arrayPir: POINTER TO ARRAY [0..20) OF INTEGER <- actualArray: arrayFinger: POINTER TO POINTER TO ARRAY [0..20) OF INTEGER 4- @ a rrayPir,
actualArray[1]. 3;
arrayPir[1] 4- 3; arrayPirt [1] 4- 3
arrayFinger[1] 4- 3; arrayFingertt[1] 4- 3
A fine point:
The pointer attribute BASE inhibits
automatic dereferencing in the context of subscript or argument brackets. See section 6.3.
3.5. Type determination
Every expression in a Mesa program has a type that can be
deduced by static analysis of the program text. Such analysis
is called type determination. The
language imposes constraints on the type of each expression
according to the context in which it is used. A program that does not violate
any of these constraints is type-correct:
every valid Mesa program must be type-correct.
In
principle, every variable and every expression has an inherent type derived from its
structure. The inherent type of a variable is established by
declaration: the form of a literal implies its type. and each
operator produces a result with a type that is a function of the types of the
operands. Inherent types of some expression forms are listed below:
Expression
34
NIL
x
< y
x array[i] Cz.x
(x e)
Inherent
Type of Expression
[34..34)
POINTER TO
UNSPECIFIED BOOLEAN
declared type of x
type specified for the components of array POINTER TO type of x
type
of x
The type rules in Mesa take two general forms, which are
the following:
The
exact type required by the context is known, and a given type must conform to
it. The required type is called the target type.
The
exact type required is not implied by context, but a relation that must be
satisfied by a set of types is known. The process of
satisfying that relation is called balancing.
Situations
in which the target type is known are simpler and more common; they
will be discussed first.
All
assignment-like contexts establish a target type for the expression to be
assigned. These contexts include not only assignment itself (where the
target type is the type of the LeftSide) but also initialization,
record construction (where the target type for each component expression is the
declared type of the corresponding field). array
construction, parameter list construction, and the like.
![Text Box: = RECORD[c: CTjpe]:](23a-MesaManualOCR_files/image037.gif) Example:
Example:
LType: TYPE War. LType: . . .
War 4- anyExp:
War f- LType[c: someExp]: Ware 4- someExp:
-- target type of anyExp is LType
-- target type of someExp is CType
... which is more obvious here
The following rule applies to assignments:
There is never any automatic
dereferencing or type conversion of any kind for the LeftSide
of an assignment, and the inherent type of the LeftSide
is the target type of the right
side. (Of course, a LeftSide may contain subexpressions,
such as array subscripts, that are themselves right
sides and subject to conversion.)
Certain other contexts imply a target type. For example,
the target type for an array subscript is the index type of the
array. Also, the target type of the expression following IF, WHILE, etc., is BOOLEAN.
If the inherent
type of an expression is equivalent to the target type, the use of that
expression is type-correct. If it is not equivalent, it may
still be possible to obtain conformance by applying various
Iype conversions, which
are sometimes called coercions. In
Mesa, there is at most one sequence of conversions that can be applied
automatically to convert a value from one type to another. When implicit
conversion from the inherent type to the target type is impossible, the program
is in error; e.g..
assigning a BOOLEAN value to an INTEGER variable is !WWI- valid.
Some
fine points:
When
the target type is well defined. certain expression forms may be abbreviated.
Identifier constants need not be qualified. and explicit identification of the type of a
constructor is optional. The abbreviated constructs have no inherent type when viewed
out of context. and they cannot be used in situations requiring implicit conversion. For example.
R: TYPE = RECORD [i: INTEGER]:
w R [R[3]]: --
the second R cannot be omitted
An Extractor never has
an inherent type: the extraction is controlled by the inherent type of the RightSide,
which therefore cannot
be abbreviated or converted. For
example.
r: RECORD [inner: RECORD[fl. j2: INTEGER]]:
jj 4- r.inner: --
the field
selection cannot be omitted
3.5.1. Type conversion
There
are four automatic type conversions that can be applied to establish type conformance.
All have been discussed in preceding sections. They are the
following:
(1) A
value with a subrange type may be converted to a value with its base type, and
vice versa
(section 3.1.2).
(2) A
value with a single-component record type may be converted to a value with the
type of that component (section 3.3.2).
(3) A
value with a short numeric, pointer or array descriptor type may be lengthened
to a value with the corresponding long type (section 2.4.5).
(4)
A value with any numeric type may
be converted to type REAL (section 2.4.5).
The first of these is a somewhat special case; as
mentioned in section 3.1.2, it is more accurate to view
this as a pair of conversions that are applied unconditionally when evaluating,
and assigning to, a subrange variable.
Examples:
r RECORD [f INTEGER];
is INTEGER;
ii: LONG INTEGER;
i r, - i 4- rf
ii f r, ii - LONG[nj]
|
Some
|
fine points:
A number of the
conversions used to achieve conformance require computation recursively to the constituents
of constructed types. For example. INTEGER conforms ARRAY IndexTve OF INTEGER does not conform to
ARRAY IndexType
OF LONG discusses the concept of
"free" conformance and the rules governing such co
There is one other automatic conversion. dereferencing. that is
applied only in certain 3.4.4). It is never applied
automatically to achieve type conformance in an
|
and cannot be
applied to LONG INTEGER. but INTEGER.
Section 3.5.3 ses.
syntactic contexts
(section assignment.
|
Sometimes it is necessary to subvert Mesa's type checking.
particularly in programs that manipulate low-level representations of objects. A Primary with the form
LOOPHOLE [ Expression . TypeSpecification ]
has the same value as
the Expression (viewed as a sequence of bits) and the type denoted by TypeSpecification. This
"comersion" never requires an computation. The only restriction is
that values with the
inherent type of Expression must be represented in the same number of machine
words as values of the
type TypeSpecification. When the target tn.pe is well-defined. the TypeSpecification mm be omitted.
 For example:
For example:
b: BOOLEAN: n: CARDINAL:
n LOOPHOLE[b. CARDINAL]: n LOOPHOLE[b]:
Since LOOPHOLE bypasses most checking, its use should be limited as much as
possible.
3.5.2. Balancing
*
Many of Mesa's operators are generic; i.e., the operation
performed depends upon the types of the operands. Examples are the
fundamental operators = and #, which accept two operands with arbitrary
(but compatible) types and produce a BOOLEAN result. In this case,
neither operand has a defined target type. Instead, it is necessary to
find some type to which the inherent type of each operand
conforms; any automatic type conversions are applied to the operands as
necessary to produce values of that type; and the operation is
then performed. The common type is the "least upper
bound", i.e., the one requiring the fewest conversions.
Examples:
R: TYPE = RECORD[f
INTEGER];
RR: TYPE = RECORD[ff: LONG INTEGER]:
i:
INTEGER;
ii:
LONG
INTEGER:
rl, r2: R;
rr. RR;
i = ii LONG[i] = ii
rl
= r2 compared
as records
rl = i rl.f = i
rl = rr LONG[rLJ] = rrl
Balancing
is also applied to IF expressions
(section 4.2.1). SELECT
expressions (section 4.3.3), and the arithmetic
and relational operators.
Fine
points:
Many generic
operators do not propagate the target type of the expression in which they
appear: instead. the operands
are balanced and combined to produce a result that is converted further if
necessary. For example.
ii I- i + r. ii
4- LONG[ i + rut]
ii LONG[i] + r. ii LONG[i] + LONG[ri]
The
current version of Mesa does not fully implement balancing
when lengthening (or conversion to REAL) is required. The restrictions are:
Operands of MIN and MAX
and the alternatives of conditional expressions are lengthened to match the expression's target
type, if any. and otherwise to match the type of the first operand.
The endpoints of an
interval in the right operand of IN are lengthened to match the type of the
left operand. but the
left operand is -
never lengthened.
The expressions
selecting the arms of a selection (section 4.3) are lengthened to
match the type of the selecting
expression, but that expression is
never lengthened.
3.5.3. Free
conformance *
A number of the conversions used to achieve conformance
require computation and cannot be applied recursively to
establish the conformance of types constructed from pairwise conforming types.
For example. INTEGER conforms
to REAL. but
the conversion from INTEGER
to REAL transforms the representation. Thus a POINTER TO INTEGER and
POINTER TO
REAL cannot
validly have the same referent, and these types do not conform.
the relation of free conformance is
less restrictive than strict type equivalence but is defined so that it can be
computed recursively. Loosely speakine, one type freely conforms to another if
a value of the first can always be used as a value of the second
without any computation or run-time check of validity. The relations of
equivalence. free conformance and conformance are not independent. Equivalence
always implies free conformance: if two types are equivalent, each freely conforms
to the other. Also, free conformance implies conformance: if
one type freely conforms to another, the first also conforms to the
second.
Of the automatic conversions discussed in section
3.5.1, only a restricted form of the first (subrarige conversion)
can be applied to establish free conformance. The restriction (which arises
from the representation of subrange values in Mesa) is the following:
The subrange type T[i.j] conforms
freely to T if i = FIRST[ T] and to Tji..k] if
j
< k.
If automatic conversion (1) of section 3.5.1 must
be applied in any other circumstance or if application of
conversion (2), (3) or (4) of that section is required to establish the
conformance of two types, they do not conform freely.
Of the constructed types discussed in this chapter, array
and pointer types also have rules for free conformance less
restrictive than equivalence.
To summarize:
One array type conforms freely to another if the index
types are equivalent and the component type of the first
freely conforms to the component type of the second (section 3.2.1).
One
pointer type freely conforms to another whenever the first pointer type
conforms to the second as defined in section 3.4.1.
Free conformance is also important for procedure types
(section 5.1) and variant records (section 6.4).
In the following pairs of
types, the first conforms to the second (but does not freely conform):
[0..100) [0..10)
[5..10) [0..10)
INTEGER REAL
POINTER
TO Person LONG POINTER TO Person
In the following
pairs, the first type
freely conforms to the second (but is not equivalent):
POINTER
TO [0..10) POINTER
TO READONLY [0..100)
POINTER TO READONLY [0..10) POINTER
TO READONLY [0..100)
ARRAY
[0..10) OF [0..10) ARRAY [0..10) OF CARDINAL
Fine
point:
Note that POINTER TO [0..10) does not
conform to POINTER TO [0..100) so that the following is illegal:
p: POINTER TO [0..10): q: POINTER TO
[0..100):
q p: qt - 99: -- now pi- =
99
3.6. Determination of representation *
This section discusses the rules used by Mesa for choosing
between signed and unsigned versions of the numeric operations.
These rules assume that there are conversion functions (taking the form of range
assertions, section 3.1.2.2) that convert values from CARDINAL to
INTEGER (from
LONG CARDINAL to
LONG INTEGER) and
vice versa. In both directions, the "conversion" amounts to an
assertion that the value is an element of INTEGER fl CARDINAL (LONG INTEGER fl LONG CARDINAL). Such assertions must be verified by the programmer.
For any arithmetic expression, the inherent representations of
the operands and the target representation of the result are
used to choose between the signed and unsigned versions of the arithmetic and relational operators.
The target type determines the target representation. The
preceding section describes the derivation of target types; in
addition, a range assertion establishes the asserted type as the target type of
its operand. If all valid values of the target type are
nonnegative, the target representation is unsianed: otherwise,
it is signed. The arithmetic operators propagate target representations
unchanged to their operands, but the target representation of an
operand of a relational operator is undefined. The target
representation is also undefined in all other cases in which the target type is
undefined. Thus each (sub)expression has at most one target
representation.
The inherent representation of a Primary is
determined by its type (if a variable, function call, etc.),
by its value (if a compile-time constant), or explicitly (if a range
assertion). Possible inherent representations are signed
and unsigned; in addition, a compile-time constant in INTEGER fl CARDINAL or a
Primary with
an inherent type that is a subrange of INTEGER fl CARDINAL is
considered to have both inherent representations. Inherent representations
of operands are propagated to results as described below.
The operation denoted by a generic operator is
chosen by considering first the inherent representations of its
operands, next the target representation. and finally a preferred default. If
the operation cannot be disambiguated in any of these ways,
the expression is considered to be in error. The exact rules follow:
If
the operands have exactly one common inherent representation, the operation
defined for that representation is selected (and the target
representation is ignored).
If the operands have no common inherent representation
but the target representation is well-defined, the operation
yielding that representation is chosen, and each operand is "converted"
to that representation (in the weak sense discussed above).
If the operands have both inherent
representations in common, then if the target representation
is well-defined it selects the operation; otherwise the sianed
operation is chosen.
If
the operands have no representation in common and the target representation is
ill-defined, the expression is in error.
In all cases, the inherent
representation of the result is determined by the selected operation.
The
unary operators require special mention. Unary minus converts its argument to a
signed representation if necessary and produces a sianed result.
Example:
If ni
and n have
unsigned representation, both the following are legal and assign the same bit pattern
to i, but
the first overflows if in < n.
i Ill– 4- IF in
>= n THEN
in—ii ELSE —(n—///):
ABS is
a null operation on an operand with an unsigned representation: it always
yields a value with unsigned representation. The target
representation for the operand of LONG (or of an implied lengthening operation) is
unsigned.
Examples:
INTEGER: m, n: CARDINAL; S. [0..7777713]; b: BOOLEAN
-- the statements on each of the following lines are equivalent.
|
i 1n+11: i (- INTEGER [in + tx]
PI- //: i 1 j+ INTEGER [n]
.5-1- t: 1 4- INTEGER [s] INTEGER [t]
ti 4- s+ t; n 4- CARDINAL [4+
CARDINAL [t] S s— s
4- CARDINAL [s] — CARDINAL [t]
b <- s— t > 0; b r INTEGER [s] — INTEGER [t] > 0
|
unsigned addition
signed addition
signed (overflow possible)
--
unsigned (overflow impossible) unsigned
(overflow possible)
signed (overflow impossible)
|
|
i
|
— I
|
-- INTEGER [m]
|
|
|
/ 4‑
|
in+ n*(j+ n):
|
i 4-
|
INTEGER [m] + (INTEGER [//]*( j+ INTEGER Pip)
|
|
11 4-
|
in+
n*(j+ 11);
|
n
|
+ (//*(CARDINAL [j] -I- /))
|
|
|
i 4-
|
in+ n*(s+ n);
|
1 4-
|
INTEGER [ni+(e(CARDINAL [s]+ n))]
|
|
|
b
|
S IN [1-1 ..
|
1+1];
|
b INTEGER [s] IN [INTEGER
[t
|
— .. INTEGER [t-1- 1]]
|
|
FOR
|
S IN [t—
1 ..
|
t-i- 1]
|
FOR S IN [CARDINAL[!— 1] ..
|
CARDINAL [t+ 1]1
|
|
|
|
|
|
|
The following statements are incorrect because of representational ambiguities. b i > 12: b i+ n IN [s j]
SELECT i FROM in
=> ...; t => ...; ENDCASE
CHAPTER 4.
ORDINARY STATEMENTS
Statements are the units of action in Mesa; they
control the flow of execution and the updating of variables.
This chapter treats ordinary statements:
those statements having wide applicability (such as assignment statements):
later chapters cover the remaining statements. The following syntax lists the
phrase names of all the statement
forms covered in this chapter:
Statement :: = AssignmentStmt
I IfStmt SelectStmt NuliStmt I
Block I GotoStmt LoopStmt ExitStmt I
...
Some statements have expression counterparts,
with the same general purposes but slightly different constraints.
For instance, assignment can be performed by an expression as well
as a statement. The expression forms covered in this chapter are
Expression = I AssignmentExpr IfExpr SelectExpr
In Mesa. certain statement forms such as the IF statement contain other statements. These statements in
turn may contain still other statements, and so forth. Consequently. the term
"statement" should be understood to encompass the large and small alike.
The dynamic successor of a statement embedded
within another depends upon the embedding form. For simplicity, the discussion
assumes that most statements occur in the middle of a hypothetical series of
statements. Execution paths within a statement are described for each form of
control statement and the successor is described in terms of a
postulated "Next-Statement".
Next-Statement represents nothing more than
completion of a given statement; another statement may or may not appear
at that point in an actual program.
Although
execution of a statement can be aborted prior to its normal completion. the
discussion of statement sequencing also assumes normal
termination of each statement unless otherwise stated.
In
the examples, Stmt-0, Stmt-I,
Stmt-2. etc. denote arbitrary statements, the details of which are
irrelevant.
4.1. Assignment
statements
Syntax:
AssignmentStmt =
LeftSide RightSide
Extractor RightSide
The RightSide must be an expression with a
type conforming to the type of the left-hand side. The
left-hand side must be a valid recipient of data such as a declared variable or
a component. For assignment statements,
a left-hand
side may also be an extractor (section 3.4.5).
Examples:
i 3: a (- b+c;
birthDa•.month 4-
Apr; birthrable[Totn].year
4- 1955:
[mm. dd. )31 4- birthDay: --
an extractor as the LeftSide
4.1.1. Assignment
expressions
Assignment operations may be carried out by
expressions. as well as by assignment statements. The syntax for an assignment expression is
AssignmentExpr = LeftSide RightSide
Assignment expressions can be
used for performing,
multiple assignments in a single statement, and for saving the
value of an intermediate expression without having to write a separate
statement:
x2 4-
xl 4- x0 4- v: -- set x0, xl, and
x2 to the value in v
array[' 4-
j+1] x[I]: j is changed while
changing the array component
Evaluation of the first statement proceeds as if it were written:
x2 4- (xl 4- (x0 <- v))
Note
that x2 (- (...) is
an assignment statement. The
assignment
expression, x0 +- v, yields the value assigned to x0, this becomes the RightSide
value for the other assignment expression, and so on.
There are two differences between an assignment expression
and an assignment statement:
The expression yields a value (in addition to performing
assignment).
The LeftSide of an assignment expression cannot be an
extractor.
An AssignmentExpr is an Expression. Its
type is the type of the LeftSide. and its value is the value
actually assigned (possibly after type conversion) of the RightSide. The
assignment operator has the lowest possible precedence. As a rule, an assignment
expression embedded in another expression is enclosed in parentheses.
A
fine point:
In an expression
such as the following:
a[k-k+ 1] + b[kl:
the order of evaluation is undefined. and the embedded
assignment may be executed either before or after evaluation of 44 Such use of
embedded assignments should be avoided.
4.2. IF statements
An IF statement is a control statement that functions as a two-way
switch:
IfStmt = IF Predicate ThenClause
ElseClause
Predicate = Expression
ThenClause = THEN Statement
ElseClause = empty
ELSE Statement
A simple IF statement
is shown below.
IF v= 0 THEN WriteStringrDone.1 ELSE V 4- v-1:
:Vext-Statement
'the BOOLEAN expression ( = 0) is called the Predicate of the IF statement. The Predicate is evaluated
first, and if TRUE, the
Statement in the ThenClause is executed (in this case a call on the
procedure WriteString). Upon
its completion. execution continues at Next-Statement. If the Predicate value is FALSE. the
Statement in the ElseClause, "v f v-1", is executed: if
there is
no ElseClause control
goes directly to iVext-.S7atement.
Other examples:
IF (flag = on) AND i IN [1n../71 THEN i 4- i + iDella ELSE i M;
IF winner
— = NIL THEN
BEGIN • --
this Statement is a block (section 4.4)
totalAge F totalAge +
winner.age;
IF winnerparty = Democratic THEN demoScore E demoScore+ 1 ELSE gopScore 4- gopScore+ 1;
END; --
end of the ThenClause
Note that a semicolon cannot
follow a ThenClause when an ElseClause is present.
If the Statement in a ThenClause is a second IF statement, then the outer IF may
have an ElseClause only if the inner one does;
i.e., an ElseClause "belongs" to the innermost possible IF. For example:
IF a >= 0 THEN
IF
a> 0 THEN b 1 -- a > 0 means set b to 1
ELSE b F 0: -- a = 0 means set b to 0
--
no action if a
< 0
It is recommended that "IF...THEN IF" combinations
be avoided entirely unless the second IF has an ElseClause. Often,
a single IF statement
is sufficient. For example, let p1
and p2 be
arbitrary predicates. Then the
following two statements have
identical effect:
IF pl AND p2 THEN Stmt: --
recommended form (see section 2.5.3)
IF p1 THEN IF p2 THEN Stint: --
longer form
Fine
point:
If the Predicate is a
compile-time constant. the compiler does not produce object code for the text
that would never be
executed. This also holds for IF
expressions.
4.2.1. IF expressions
•
The IF statement
has a counterpart that is an expression. Its syntax is similar to that of an IfStmt:
IfExpr = IF Predicate THEN Expression
ELSE
Expression
There are two differences between an IfExpr and an
IfStmt:
The clauses of an IF expression contain expressions, not statements;
An IF expression
must have an ELSE-clause.
Examples:
slope 4- IF y = 0 THEN max ELSE x/ y; -- avoid division by zero.
b 4-
IF
a> = 0 THEN OF a>
0
THEN 1 ELSE 0) ELSE —1;
Evaluation of an IF expression begins with evaluation of the Predicate
(in the first example, y=0). If
it is TRUE, the
expression in the ThenClause (i.e.,
max) is evaluated, and its value becomes the value of the IF expression. If the predicate is FALSE, the ElseClause expression
(i.e., x/j') is evaluated, and its value becomes the value of
the IF expression.
The second example sets the value of b to
—1. 0. or +1, depending on whether a is negative, zero, or
positive, respectively.
"lhe ThenClause and
ElseClause expressions must conform to some common type (possibly after
type conversion, as outlined in section 3.5.3): The type to which they conform
is the IF expression's
inherent type.
An IF operator
has the same precedence as an assignment operator, i.e., the lowest possible precedence.
IF expressions should be
enclosed in parentheses when embedded in other expressions.
4.3. SELECT statements
The SELECT statement chooses for execution at most one
statement from an ordered list. of statements. The
choice is based upon the relation between a given expression and expressions associated
with each selectable statement. Thus, this statement form permits multiway
branching, not just the two way branching of an IF statement.
A SELECT statement
is shown below. The separator " = >" should be read as
"chooses." The entire statement may be read as
follows: "Select, using x's value, from the comparisons preceding the
substatements. First, (x's value) 'equal to zero' chooses Stint-1. Second, 'in subrange in through n' chooses
Stint-2. Third, 'less than in' chooses Stmt-3. Otherwise, choose
nothing."

The next four sections cover various forms of SELECT, their precise syntax, and
the expression counterpart of the SELECT statement. The term "SELECT", used by itself, includes
both statement and expression forms.
4.3.1. Forms and options for SELECT Syntax
equations:
SelectStmt = SELECT Leftltem FROM -- (the head)
StmtChoiceSe ries -- (the arms)
ENDCASE FinalStmtChoice -- (the foot)

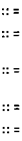
 Expression
Expression
TestList => Statement
StmtChoiceSeries TestList => Statement
:
empty
I
=> Statement
Test I TestList , Test
Expression
I -- no operator implies an
equality test RelationTail
|
Example:
I: [0..5]:
SELECT 1 FROM
0 => i i+ 1:
< 3 = > BEGIN j (-
=5 => 0:
ENDCASE => 1 (-
Next-Statetilerii
|
1: i I— I END:
1.
|
-- 1=1 or 1=2
-- 1=5
=3 or 1=4 (none of the above)
|
In the execution of a SELECT statement. the Leftltem is
evaluated first: a sequence of comparisons then follows. Each arm of the SELECT statement begins
with one or more Tests. The Expression in
each Test is evaluated
and compared with the value of the Leftltem. The evaluation occurs. in order,
from left to right. and continues until a comparison succeeds or the TestList
for that particular arm is exhausted. If a test succeeds,
control passes immediately to the statement following the
TestList in that ari-n (no further Tests are evaluated, even in
that same list). If all Tests in a Riven arm fail, the next arm in the
series is tried. After a test succeeds and its associated statement N
executed. control passes to Next-Statement.
Thus at most one statement can be chosen in a given execution
of a SELECT statement.
When combined with the Leftltem (perhaps with an
implied "="). each Test must be a valid Relation.
The type of the Expression in a Test must conform
to the type of the Leftltem. If a Test uses "IN Su
brange", the base type of the subrange must
conform to the type of the Leftltem.
A single SELECT arm may specify more than
one test:
SELECT
i*j+ k FROM
1.
IN [7..10] => Stint-1: -- values: 1, 7, 8, 9, 10
2, 5, > 10 = > --
values: 2, 5, 11, 12. ...
ENDCASE:
A final choice may be
appended to a SELECT to
handle all remaining cases: it follows ENDCASE. For example:
PriorityState: TYPE =
RECORD[i0, II, 12, i3: BOOLEAN]:
oldS rate, new.Slate:
SELECT TRUE
oldState.i0
oldSlate.12. oldStale.i3,
ENDCASE
FROM -- picks
=>
newSlate.10 =>
news late. lI =>
nen'Siate.12 =>
=>
the
first TRUE state:
Smii-0:
Stint-2:
Sunt-3;
511111-99:
If this SELECT statement does not choose
one of the first four statements, the final statement (Stunt‑
99) is executed.
Fine
points:
If all SELECT arms (or those in some contiguous
subseries) specify constant values in each Test, the compiler can produce code using a "jump
table" for efficient selection.
The other alternatives for SelectStmt
apply to variant records and are discussed in Chapter 6.
4.3.2. The
NULL
statement
'ale
NULL statement,
which serves only as a placeholder, is often useful as the statement in an arm
of a SELECT
statement:
NullStrnt = NULL
For example:
4.3,3. SELECT expressions
The SELECT statement
has an expression counterpart. There are three differences between the expression
and statement forms of SELECT:
(1) The
choices in each arm must be expressions, not statements.
(2) The
arms are terminated by commas, not semicolons.
(3) ENDCASE must be followed
by ' =>" and a final (expression) choice. Its
syntax is defined by
SelectExpr = SELECT Leftltem FROM -- (the head)
ExprChoiceList -- (the arms)
ENDCASE => Expression -- (the
foot)
I •-•
ExprChoiceList = TestList => Expression ,
ExprChoiceList TestList => Expression ,
LeftItem and TestList are defined in section
4.3.1.
For example:
pt: INTEGER: --
Point on a line.
lo, hi: INTEGER 4- 0: -- Bounds for a
line segment, initially a null segment
PoiniPosition: TYPE = flefiMargin,
rightMargin, inside, outside, degenerate}: position: PointPosition:
|
position 4- SELECT pt FROM
IN (lo..hi) => inside,
NOT IN [lo..hi] => outside,
< hi lefiAlargin,
> lo => righatfargin,
ENDCASE => degenerate;
|
=lo but # hi
= hi but
# lo
lo and = hi
|
A SELECT
expression is executed just as a SELECT statement,
except that the selected arm yields a value, which becomes the
value of the SELECT expression
as a whole. The inherent type of a SELECT expression is the one to
which all the expressions in the arms conform (section 3.5.3).
A SELECT operator has the same precedence as an assignment
operator, i.e., the lowest possible precedence. SELECT expressions
should be enclosed in parentheses when embedded in other expressions.
4.4. Blocks
A
block is a way of packaging a series of statements so that they can be used
where only a single
statement is permitted syntactically. In its simplest
form a block is a pair of "brackets", BEGIN and END. with a series of
statements (of any form) between them. The general syntax is
 = BEGIN
= BEGIN
OpenClause
EnableClause DeclarationSeries
StatementSeries ExitsClause
END
-- optional; section 4.4.2 -- optional; section 8.2.1 -- optional
-- optional; section 4.4.1
StatementSeries =
empty I
Statement
I
Statement
StatementSeries
DeclarationSeries =
empty I DeclarationSeries Declaration
A fine
point:
A semicolon terminates ex en. declaration and
therefore is not mentioned as a separator here.
In the following IF statement, a block takes the
place of the single Statement normally allowed in a
ThenClause:
IF lo > hi THEN
BEGIN
-- Exchange /o and hi. temp: INTEGER 4- lo;
lo - hi:
hi 4- temp:
END
A semicolon must separate each statement in the StatementSeries
but is optional after the last statement.
The optional DeclarationSeries in a block
introduces new identifiers, such as temp
above, with scope smaller than an
entire procedure (or module) body. Scope is discussed further in sections 4.4.2
and 5.5.1 and in chapter 7.
Fine
point:
Durine the execution of
a Mesa program. frames are allocated at the procedure and module level only
(section 5.2). Any
storage required 13x variables declared in an internal Block (one used as a
Statement) is allocated in the frame of the smallest enclosing procedure or
module. When such internal blocks are disjoint. the areas of the frame used for their
variables overlayone another.
Ordinarily, when a block is executed, every statement in
its StatementSeries is executed,
and Next-Statement is
the successor of the entire block. It is possible, however, to jump out of a
block, as
described in the next section on GOTOS.
4.4.1. GOTO statements
A more general form of a block allows a series of labeled
statements to be written immediately preceding its END. One
can jump to any one of these statements from within the block only, using a GOTO statement.
There are two consequences of this way of constraining the GOTO:
A GOTO may only jump forward in
the program, never backward.
A GOTO may only jump out of a block, never into one.
The syntax for the ExitsClause
of a block and for the GOTO statement is the
following:
ExitsClause
ExitSeries
LabelList
Label GotoStmt
= empty I
EXITS ExitSeries
EXITS ExitSeries
: --
optional final semicolon
= LabelList => Statement I
ExitSeries La belList =>
Statement
= Label I LabelList .
Label = identifier
= GOTO
Label I GO TO Label
A simple example:
IF input.status open THEN
BEGIN
IF inputfilellandle = default Input THEN GOTO useDefault;
--
processing for non-default file
IF inputfileNumber = ityNumber THEN GOTOfik/SDefauit;
IF input.length = 0 THEN GOTO newFile:
-- compute number of pages in the file
EXITS
useDefault,fileIsDefault => -- multiple
labels are allowed
BEGIN input 4- itylnput; pages'- maxPages END;
newFile => pages 4-
0;
END; --
end of the ThenClause and the IF statement
Next-Statement
The Labels in this example are useDefault, filelsDefault, and
newFile (it
is helpful to view the labels as the names of conditions
or reasons for which the block is being left). If any one of the GOTOS is
executed, control transfers immediately to the statement
labeled with the identifier used in the GOTO. The normal successor of any
one of the labeled statements is Next-Statement,
which is also the normal successor of the last
statement in the main body of the block (i.e., the one just before EXITS).
Since one block can
appear within the body of another, a GOTO can jump directly out of one (or more)
blocks to the ExitsClause of an enclosing block. For example,
BEGIN
•
BEGIN . . .
IF i = iMax THEN GO TO endOfArray: . . .
END;
. . .
i i+1;
EXITS
endOfArray
=> i 0;
END;
Next-Statement
-- outer block -- inner block
-- jump to end of outer compound --
end of inner
-- end of outer
If the GOTO statement is executed, control jumps to the exit labeled endOfArray. The chosen statement
(i4-0) is executed and control then goes to Next-Statement. The identifiers
used as Labels are only known inside the block in which they
appear, and it is possible to use the same identifier as a
label in a number of blocks. If this is done in nested blocks, a GOTO naming that
identifier will always go to the statement with that
label in the smallest enclosing block. Generally, using the same label
in nested blocks is a bad idea.
Since Mesa allows declarations in any block, it
is possible to declare a. procedure (section 5.5) within the
scope of the Labels of a block. Jumping out of a procedure into a surrounding
block is disallowed. Such a result may be obtained, however, by
use of the SIGNAL machinery
(see chapter 8). For example. the following is illegal:
BEGIN
· • -
p: PROCEDURE =
BEGIN
GOTO
pankEx illegal GOTO
END;
·
• la •
EXITS
panicExit =>
END
The desired result is achieved with the following program
(see chapter 8 for a description of signals and catch phrases):
BEGIN
Panic: SIGNAL = CODE;
- • •
p: PROCEDURE =
BEGIN
... SIGNAL Panic; END;
. . . p[ ! Panic
=> GOTO panicExit]; .
EXITS
panicExit =>
END
A statement in an ExitsClause may contain a GOTO, but
the label in the Go-ro
can only refer to labels in surrounding
blocks, not to labels in the same ExitsClause as the GOTO. For
example, the following is legal:
|
BEGIN
BEGIN
EXITS
endOfFileReached => BEGIN
END;
EXITS
out0fData => .;
END
|
-- outer
-- inner
GOTO outOlData END;
-- end of inner
-- end of outer
|
4.4.2. OPEN clauses
An OPEN clause allows more convenient reference to the fields of a
record. In the simplest form, it allows fieldname as an abbreviation
for recordname.fieldname. If
the name of the record is complicated (e.g., candidateList[table0fObjects[i]]), this
can make programs much more readable. The programmer should be
cautioned, however, that this is merely a syntactic shorthand: the code
generated is actually recordname._fieldname.
Thus in the example above, if i or table0fObjects is changing within
the scope of the OPEN,
each reference to a field can potentially access a
different element of candidateList.
The syntax for OPEN follows:
OpenClause =
empty I OPEN OpenList
: -- note the
terminal semicolon
OpenList =
OpenItem OpenList . Openitem
OpenItem = AlternateName :
Expression I
Expression
AlternateName = identifier
'11-ie scope of
an OPEN clause
(the portion of the program over which the synonym can be used) is the
body of a block or loop, including
the optional exits clause (section 4.5). The following diagram summarizes
the scope of the various parts of a Block. The scope of each phrase
extends over others with greater indentation.
BEGIN
OpenClause
EnableClause
Decla rationSe ries StatementSe ries ExitsClause
END
An
Openitem using an AlternateName allows a simple identifier to replace an
expression as the designator of some record object. For example,
the two blocks below are equivalent:
PersonChain: TYPE = RECORD [p:POINTER TO Person, next: POINTER TO PersonChain] candidateList: POINTER TO PersonChain: -- Person is
defined in section 3.5
BEGIN
OPEN c: candidateList.p;
IF c.party = Republican AND c.age < 30 THEN youngRepublicans F youngRepublicans+1; IF c.sex = Female THEN women
4- women+ 1;
END BEGIN
IF candidateList.p.party =
Republican AND candidateList.p.age
< 30 THEN youngRepublicans
4- youngRepublicans+1;
IF candidateList.p.sex = Female THEN women n-• women+ 1;
END
The OPEN statement does not provide a general renaming capability;
it merely allows more convenient access to the fields of a record.
Each Expression in an OpenList must either have a record
type or be a pointer to a record. When the AlternateName form is used, the
alternate identifier always designates the opened record, even if the Expression
is a pointer to that record.
The form of OpenClause without an AlternateName
allows access to the fields of a record object as though they were
simple variables. For example, using this feature in the above example allows
omission of the "c."s:
BEGIN
OPEN candidateList.p;
IF party = Republican AND age< 30 THEN youngRepublicans 4- youngRepublicans+ 1; IF sex = Female THEN women
4- women+1;
END
Note, if the AlternateName form is used qualification of record fields using
the alternate name is mandator
Besides record objects. one can open a module (chapter 7)
to simplify access to the identifiers available from the module.
If an OpenClause contains multiple
Openitems, the opened expressions might refer to records having
some selector names the same. In the example below. x is a selector name for
two records. recrar and
recVar.subRecord. An
unqualified occurrence of x is taken to be the x component of the
rightmost opened record (rec
Var. sub R eco rd). To refer to an earlier
opened record. explicit
qualification is
necessary (the AfternateName
form should be used).
INTEGER:
RecordType: TYPE = RECORD
a, b, x: INTEGER,
subRecord: RECORD[x, y:
INTEGER]
1:
recVar: Recordrype;
BEGIN
OPEN rl: recVar, recVar.subRecord:
i ?-1.a + rl.b* rl.x: j
x—y:
END:
The above block is equivalent to:
BEGIN
i +- recVar.a + recVar.b * recVar.x;
j recVarsubRecordx— recVarsubRecord.y:
END:
Fine
points:
The range of text
affected by an Openitem includes any further items in the OpenList. The
OpenClause itself may
use implied qualification or alternate names (from earlier Openitems).
Opened expressions are evaluated at each use, whether used implicitly or
explicitly under an alternate name. This is essential for dealing with
relocating allocation schemes. To avoid confusion, however. it is recommended that ordinary
pointers be updated before entering the statement sequence headed by an
OpenClause. In that way. names in the statement sequence will remain
consistent. i.e., will apply to the same
objects throughout.
4.5. Loop statements
In Mesa, a loop is a statement containing a
series of statements that are to be executed repeatedly. All the ways of controlling how many times a loop
should be repeated include the ability to repeat it zero times: i.e., to bypass it entirely. Example
1 in section 2.1 contains the following loop statement:
UNTIL n = 0
DO
r 4-
In MOD n: r gets remainder of tn/n
m4- n: n ry
ENDLOOP
"UNTIL n = 0" is
the loop control for
this loop. A variety of loop controls are available in Mesa: they include
control by a Boolean expression, as above, and control by iteration over a
subrange, as in the following example:
FOR i
IN
[0..N) DO a[i] a[i]
+ b[i] ENDLOOP
This will execute the assignment N times, with i taking the values 0, 1, ...,
N-1 on successive iterations. If
N = 0, the assignment is not executed at
all.
The formal syntax of loop statements is
|
LoopStmt =
|
LoopControl
DO
OpenClause EnableClause StatementSe ries LoopExitsClause
ENDLOOP
|
-- optional: may be empty
-- optional (section 4.4.2) -- optional (section
8.2.1)
-- optional; may be empty
|
The
portion between DO and
ENDLOOP is
the body of
a loop. Subsequent sections discuss the forms of LoopControl,
the LoopExitsClause and GOTOs in loops.
The scopes of identifiers introduced in the various
components of a loop are summarized by the following diagram
(cf. Block, section
4.4.2):
LoopControl
DO
OpenClause
EnableClause
StatementSeries LoopExitsClause
ENDLOOP
As in the case of a block, any exit labels are visible
within the EnableClause, and any catch phrase in the EnableClause is
not enabled within the LoopExitsClause.
4.5.1. Loop control
The syntax for LoopControl is
LoopControl = IterativeControl ConditionTest -- either
may be empty
ConditionTest = empty I WHILE Expression
I UNTIL Expression
If both the IterativeControl and the ConditionTest
are missing from a loop, it will repeat indefinitely
(unless terminated by an embedded
GOTO or
EXIT, section
4.5.2).
If a LoopControl includes a ConditionTest, the
Boolean expression in the test is (re)evaluated before each
execution of the loop body, including the first. If the ConditionTest succeeds, the body
of the loop is executed: if it fails,
the loop is finished (terminates conditionally) and control continues at Next-Statement (Or at a FINISHED clause,
see section 4.5.2). A WHILE
test succeeds if the value of the expression is TRUE. In
the following example, i has
the values 1, 2, 3, ..., 9 in successive executions of the body of
the loop, and the value 10 when Next-Statement
is reached (assuming that there are no other
assignments to i):
i4-1: 1 --
this statement is not part of the loop
WHILE i< 10
DO
... ENDLOOP:
Next-Statement
An UNTIL test
succeeds if the value of the expression is FALSE: i.e., it is the opposite of
WHILE. The
following loop is equivalent to the one above:
|
i4- 1:
UNTIL i > = 10
DO i 1+1: ENDLOOP;
Next-Statement
|
-- this statement is not part of the loop
|
An IterativeControl provides
a way
of executing a loop (no more °than) a precomputed number of times.
It may he followed by a ConditionTest. It optionally updates a specified ControlVariable prior
to each iteration so that, e.g.. statements in the body have access to (a simple
function of) the number of iterations. A loop that finishes by satisfying, the implicit test
associated with an Iteration or a Repetition is
said to terminate normally.
IterativeControl Repetition
Iteration LoopRange
Direction Assignation
ControlVariable InitialExpr NextExpr
= empty I Repetition I Iteration I Assignation
= THROUGH LoopRange
= FOR ControlVariable Direction IN LoopRange = SubrangeTC
I Typeldentifier
BOOLEAN I CHARACTER = empty I DECREASING
=
FOR ControlVariable 4- InitialExpr , NextExpr = identifier
= Expression = Expression
In the Repetition form
of IterativeControl, a
LoopRange specifies
how many times the loop
body
is to
be executed. For example,
THROUGH
[1..100] DO ... ENDLOOP
executes the body 100 times. A loop range can have any
element type (section 3.1) except INTEGER or CARDINAL. The
bounds of a subrange can be arbitrary expressions and do not have to be compile-time
constants (as they do in a SubrangeTC
used to define a type).
A Repetition and
a ConditionTest may
be combined in a single loop control. For example,
THROUGH
[low..high] WHILE linelsConnected DO ... ENDLOOP
Normal termination occurs after high— low+ 1 iterations;
conditional termination can occur sooner if linelsConnected is FALSE prior to some iteration. Note that if low > high, the interval [low..high] is empty
and the loop body is not executed.
Iteration and
Assignation, the
two forms of IterativeControl that
include a ControlVariable, begin
with the keyword FOR. The
control variable must
be a variable declared separately in the program. Its type becomes the
target type for the various expressions in the remainder of the IterativeControl.
An Iteration
steps through a subrange much as a Repetition, which is described above.
In addition, it may specify a Direction: whether to begin at the
lower bound of the range and step up (empty) or at the upper bound and
step down (DECREASING).
In any case, the size of the step is always
one; for (a subrange of) an enumerated type, this really means stepping from an
element to its successor (if the direction is increasing) or to its
predecessor (if the direction is DECREASING). The control
variable is assigned the current control value each time around the loop.
When a loop terminates normally, the final value of the control variable is not defined. The only way
to ensure that the control variable final value is well defined is to terminate
the loop conditionally or forcibly (e.g.. using EXIT or GOTO, section 4.5.2).
 The
following examples shift the components element unchanged:
The
following examples shift the components element unchanged:
 FOR i IN [1..LENGTH[rec]) DO
FOR i IN [1..LENGTH[rec]) DO
vec[i—
1] 4- ree[i]; ENDLOOP:
FOR /DECREASING IN [1..LENGTH[vec]) DO
rec[i] vec[i— 1];
ENDLOOP;
In the second case, i is initially set to the value LENGTH[rec] — 1 and
decremented by one for each subsequent iteration. During the last
execution of the loop, i has
the value 1.
Bounds expressions in a Loop Range are evaluated exactly once, before the first
execution of the loop body. Subsequent alteration of variables used in those
expressions does not affect the number of iterations. When an Iteration is
combined with a ConditionTest in a single loop control, the control
variable is updated and tested before the ConditionTest is evaluated.
In an Assignation, the value of the InitialExpr
is assigned to the control variable prior to the first
iteration. Before each subsequent iteration. the NextExpr is
(re)evaluated and assigned to that variable. There is no
implicit test associated with an Assignation as there is for an Iteration;
thus, the user must either use a GOTO (section 4.5.2) to terminate the loop or include
a ConditionTest in the LoopControl with
the Assignation. As with an Iteration, the control variable is
updated for each iteration before any ConditionTest is evaluated. This
form is useful for scanning a list structure, as in the following example:
NodeLink: TYPE = POINTER TO Node: node, headOfList:
NodeLink;
Node: TYPE = RECORD
list
Value: SomeType,
next: NodeLink --
either NIL (end of list) or pointer to next element
FOR node head0fList, node.next UNTIL node= NIL
DO ...
ENDLOOP;
A
fine point;
The control variable
can be altered within a loop. but this is not recommended. An iterative loop
control updates the
variable according to its current value. If the statement sequence assigns a
new value to the control variable, the expected series of values may be disrupted (by omission or
duplication).
4.5.2. GOT0s, LOOPS,
EXITS, and loops
A loop may be forcibly
terminated by a GOTO (or an EXIT, see below). The LoopExitsClause
serves the same purpose as the ExitsClause
in a Block; there are just three differences:
(1) The
LoopExitsClause is bracketed by REPEAT and ENDLOOP instead
of EXITS
and END;
(2) The
LoopExitsClause may contain a final statement labeled with the keyword FINISHED; this
statement is executed if the loop terminates normally or conditionally. but not if it is forcibly
terminated.
(3) There is a special case
of the more aeneral GOTO,
called EXIT, which simply terminates a
loop forcibly without giving control to any statement in the LoopExitsClause.
There
is another kind of GOTO
statement. LOOP, which does not terininate the loop but skips the remainder
of the loop body in the current iteration.
|
Syntax equations:
LoopExitsClause LoopExits
FinishedExit
LoopCloseStmt ExitStmt
|
= empty I REPEAT LoopExits
= ExitSeries I
ExitSeries ;
FinishedExit I
ExitSeries ; FinishedExit
= FINISHED => Statement FINISHED
=> Statement ;
=
LOOP = EXIT
|
The LOOP statement is used when there is nothing more to do in the
iteration, and the programmer wishes to go on to the next
repetition, if any. For
example,
stuff ARRAY [0..100)
OF Potent iallyInterestingData;
Interesting: PROCEDURE [PotentiallyInterestingData] RETURNS [BOOLEAN];
is CARDINAL;
FOR i
IN [0..100) DO
--
some processing for each value of i
IF ~ThtereStitig[Stuff[i]]
THEN LOOP; --
process meld
ENDLOOP:
The example used in
the previous section to illustrate ConditionTests can be rewritten using
a GOTO and
a LoopExitsClause as follows:
i4- 1;
DO
IF
i >= 10 THEN GOTO quit: -- first statement in the body
...
REPEAT
quit => NULL; --
do nothing but exit the loop
ENDLOOP:
Next-Statement
Frequently, forcible loop termination requires no special
processing in the LoopExitsClause. The EXIT statement simplifies this
case by not requiring a labeled statement in that clause: in fact, no LoopExitsClause
need be present. The above example can be further
rewritten to use EXIT,
as follows:
i - 1:
DO
IF i > = 10 THEN EXIT; -- first
statement in the body
i i+1;
ENDLOOP;
Next-Statement
An EXIT is less general than a GOTO. For instance, if one has a loop nested within
another and wants to exit from both, EXIT cannot be used because it
terminates only the inner loop. A GOTO can jump to the ExitsClause
of any enclosing loop or block. The ExitsClause of either a block or a loop
is considered to be outside of the block or loop. Thus. an EXIT can
appear in any ExitsClause (provided there is an outer loop).
and it causes forcible termination of the smallest surrounding
loop.
The
following example shows a typical loop that is terminated only by execution of
an EXIT statement.
Bufl ndexType: TYPE =
11..max1;
but ARRAY BufindexType OF INTEGER; x: Buf IndexType:
|
FOR 1 4- x, (IF i = max THEN 1 ELSE i+ 1) DO
IF buf[i] = 0 THEN EXIT; buf[i].-
0;
ENDLOOP;
|
Starting at point
-- do something and then
-- quit on a "clear" entry, or -- clear until
one is found.
|
The NextExp r, "IF i = max THEN 1 ELSE i+1". makes buf behave as a ring buffer.
Sometimes one must detect normal (as opposed to
forcible) termination of a loop, perhaps to take some
"finishing" action. A final labeled statement with the label FINISHED (which
may not appear
as the identifier in a Go-ro) provides this facility. For
example,
FOR i
IN [0..nEntries) DO
IF a[i] = x THEN GO TO found: REPEAT
found => old 4- TRUE;
FINISHED => BEGIN CI [1 4- nEntries] F x; nEntries 4- nEntries + 1: old
+- FALSE END; ENDLOOP;
The FINISHED exit is taken if and only if the loop terminates
normally or conditionally (i.e., when the loop range is exhausted in
the case above). Upon entry to a FINISHED exit, the value of the ControlVariable is undefined. Note that if
an EXIT statement
is executed, the FINISHED
statement is not executed.
CHAPTER 5.
PROCEDURES
Procedures provide one of the most important abstraction
mechanisms available in Mesa. The definition of a procedure
assigns a name to a function or action. The computation performed by a
procedure is specified by a series of statements and can be expressed in terms
of parameters of
the procedure. In addition, a procedure can produce one or
more values, called its results. To
invoke or call a
procedure, the programmer simply names it and supplies arguments corresponding to the parameters.
He need not be concerned with the internal workings of the procedure and can
use a meaningful name to denote the function or action.
The GCD computation in section 2.1 is of limited use as it
stands because it depends upon (and changes) variables in, n and gcd declared somewhere in its
environment. It might usefully be packaged as a procedure
with parameters in and
n. Such
a procedure is declared as follows:
Gcd: PROCEDURE [in, n: INTEGER] RETURNS [CARDINAL]
BEGIN
r: INTEGER;
UNTIL n=0
DO
r 4- in MOD n: in (- n 4-
r,
ENDLOOP;
RETURN
[ABS[m]]
END;
The parameters of a procedure constitute the fields of a
record, called the parameter
record of the procedure. When calling a
procedure, the arguments are evaluated and assembled into an argument record
using a constructor (section 3.3.4.).
"Applying" a procedure value to that argument record invokes
the procedure. Consider the procedure call Gcd[x+1, y]. This evaluates .x+1 and y, constructs an argument
record from these values, and then calls procedure Gcd, passing it the argument
record.
Within the procedure, the argument record is assigned to
the parameter record, and fields of the parameter record are
accessed as simple variables (i.e., that record is OPENed). Thus
the effect of the call above is to assign the value of x+1 to in and the value of y to it before the statements within
Gcd are
executed.
A procedure may return values to the point of its call.
These results constitute
a result record. There
may be any number of results, and their types may differ. Within a procedure, a
RETURN statement
assembles the results into a record and then returns control to the caller. The
procedure Gcd returns
a result record with one component, of type CARDINAL. Thus the form Gcd[x+1, y] is an expression
with a record type: because of the automatic conversion from a single-component
record to the component (section 3.5.1). it can also be
used in any context accepting a value of type
CARDINAL.
The following
assignment has an effect similar to that of the entire example in section 2.1: gcd Gcd[m, n]
Note
that arguments are always passed by value in Mesa. The arguments m and n (for which declarations
must exist at the point of call in this case) are completely distinct from the
parameters in and
t4. and execution of Gcd does not change the values
of the former.
A procedure declaration with the form illustrated above
is said to define an actual
procedure. It introduces an identifier, supplies some procedure type for that
identifier, and defines the computation to be performed by
specifying a block called the procedure
body. Such a declaration uses fixed form Initialization and closely parallels the
declaration of an ordinary variable with = initialization, e.g.,
octalRadix: CARDINAL = 8;
Other declaration forms may also be used, and this allows
one to have procedure variables with values that can be updated
to designate different actual procedures. In Mesa, procedures are full-fledged
data objects.
A procedure type is defined by specifying its parameter
and result records. For example, the type of Gcd is
PROCEDURE
[m, n: INTEGER]
RETURNS [CARDINAL]
Procedure types constructed with different parameter and
result records are different; thus the type system helps to guarantee that,
even when procedure variables are used, a proper argument record is constructed
for each procedure call (i.e., that the number and types of the arguments are
correct) and that the result record is used correctly in the text
surrounding the procedure call.
Since a procedure body is a block, it may contain declarations. These declare local variables for that procedure,
variables that are created when the procedure is called, may be directly
accessed only from within it, and are destroyed when the
procedure returns. Within a procedure body, the named fields
of the parameter and result records are also considered local variables; they
have the same lifetimes and can be referenced without
qualification. The local variables of Gcd are tn.
17 and r.
Because this local storage is allocated and
released dynamically, any Mesa procedure can be invoked recursively and used in
a reentrant fashion. Thus the following alternative declaration of Gcd, which directly mirrors a recursive definition of the greatest
common divisor, is valid:
Gcd: PROCEDURE [m,
n: INTEGER] RETURNS [CARDINAL] =
BEGIN
RETURN [IF
n = 0 THEN ABS [m] ELSE Gcd[n, in MOD ii]]
END:
A
fine point:
Although both versions
of Gcd compute the same function, the
recursive one is extravagant in its use of time and space (especially since an
iterative version is so easy to derive). This demonstrates an advantage
of procedural abstraction:
the second definition of Gcd could be replaced by the first
without effect on any caller
of Gcd. Examples in
section 5.4 demonstrate more appropriate uses of recursion.
A procedure body may also access variables declared
outside of the actual procedure. Such variables are nonlocal to the
procedure; they exist longer than any single invocation of the procedure and must
be defined in the enclosing program text.
Mesa also has extensive facilities supporting the separate
compilation of packages of procedures and variables; these packages
are called modules (chapter
7). Some of these facilities allow one module to name and use the
procedures in another, but the type-correct usage of argument and result records
is still checked at compile-time.
if a procedure is called from many places. the
"packaging" of code provided by the procedure body makes
a program more compact. Procedure calls and returns do. however. introduce some
runtime overhead. if a procedure is called from exactly one
place. that overhead is unnecessary: if it is called from
time-critical code or if the body of the procedure is very simple. the overhead
can he unacceptable. Mesa provides Mine procedures for
such applications. The call of an inline procedure is replaced by a
modified copy of its body. This mechanism eliminates most of the overhead
but retains many of the advantages of procedures. such as
introducing structure. improving readability and isolating
detail.
The
foregoing discussion is only an introduction to procedures. The rest of this
chapter provides further detail.
51. Procedure
types
Procedure
types are constructed by the syntactic form ProcedureTC, which is
defined as follows:
ProcedureTC = PROCEDURE ParameterList
ReturnsClause
ParameterList = empty I FieldList
Retu rnsClause = empty
I RETURNS ResultList
ResultList = FieldList
The
ParameterList and ResultList are FieldLists and define record types. If
either is missing, the corresponding record type is
"empty". A procedure type is fully determined by its parameter and
result record types.
Default
specifications are permitted for fields of a ParameterList. but every
field in a ResultList must have an empty DefaultOption,
i.e.. no default value can be specified for a result.
Some fine points:
Notice that constructors of
procedure types require specification of the field lists: it is not possible to
use a separately
defined record type to specify the complete parameter or result record.
These records. unlike regular
records, are not packed: every component is aligned (begins on a word boundary)
to allow efficient
passing of arguments and results.
A few typical procedure types are shown
below:
PROCEDURE
PROCEDURE [x: INTEGER, flag: BOOLEAN]
PROCEDURE RETURNS [i:
INTEGER]
PROCEDURE RETURNS [1: INTEGER. b: BOOLEAN]
PROCEDURE [x: INTEGER] RETURNS [y: INTEGER]
--
takes no arguments; returns no results -- takes two arguments
-- returns a
single value
--
returns two results
--
takes and returns one value
These are all distinct types; none conforms to any of the
others.
Values with procedure types are allowed in Mesa; one may
have procedure variables, arrays of procedures, records with
components that have procedure types, and procedures with procedure parameters
or results. The fundamental operations =, # and 4- may be applied to
procedure values with conforming types.
Constructors of procedure types appear most commonly in
the declarations of actual procedures, but they may occur
wherever a TypeSpecification is valid. Thus a ProcedureTC can
appear in such constructs as:
A variable declaration:
brorHandler. PROCEDURE [which: ErrorCode] DefaultHandler,
A type declaration:
ListProc: TYPE = PROCEDURE [in: List] RETURNS
[out: List]; First. Rest. Last: ListAve:
A field list (notice the parameters lessThan and swap):
.Bart:
PROCEDURE [
first.
last: CARDINAL,
lessThan: PROCEDURE [CARDINAL, CARDINAL] RETURNS [BOOLEAN], swap:
PROCEDURE [CARDINAL, CARDINAL]
I;
An array declaration:
tOps: ARRAY OpNames OF PROCEDURE [T, T] RETURNS [T];
5.1.1. Procedure values and compatibility
*
Equivalence and conformance of procedure types are
defined in terms of relations between fields of their ParameterLists and ResultLists. If the number of parameters
or results differs, one procedure type neither conforms to. nor is
equivalent to, another. Otherwise, corresponding fields, matched
according to position, are considered. Two procedure types are equivalent if,
for each pair offields, the names are identical (or both are
unnamed), the types are equivalent, and both DefaultOptions
are empty. One field is compatible with another if the names are identical or if either
is unnamed, and if the types are equivalent. A procedure type conforms to
another if all corresponding fields are compatible. Default
specifications do not affect conformance.
All the assignments in the following example are valid
because the types of the procedures conform:
Handle: TYPE = POINTER TO Person;
SignedNumber: TYPE = INTEGER:
Int: TYPE = INTEGER:
ProcA: PROCEDURE [h: Handle, v: SignedNumber];
ProcB: PROCEDURE [h:
Handle, v: Int];
ProcC: PROCEDURE [POINTER
TO Person, INTEGER];
ProcA 4- ProcB: ProcA 4".
ProcC:
ProcC t IF flag THEN ProcA ELSE ProcB;
Fine
points:
In the current version of Mesa, the
name of the component of a single•element parameter or result record is ignored when comparing two procedure
types for conformance.
If one procedure type
conforms to another, it also conforms freely (section 3.5.3). Free conformance
of procedure types is
actually defined by the following less restrictive rule: One field is
compatible with another if the names are identical or either is unnamed. and if the type of the
first freely conforms to the type of the second. One procedure type freely conforms to another if.
for the ParameterList. each field of the second is compatible with the corresponding field of the first and, for the ResultList. each field of the first is compatible with
the corresponding field of the second.
In the following example. recall that Handle conforms freely to ReadOnlyHandle but not vice versa:
|
ReadOnlyHandle: TYPE =
ProcX: PROCEDURE [in:
ProcY: PROCEDURE [in: ProcZ:
PROCEDURE [in:
-- valid assignments
ProcY ProcX: ProcZ
|
POINTER TO READONLY Person:
ReadOnlyHandle] RETURNS [out: Handle]: ReadOnlyHandle]
RETURNS [our. ReadOnlyHandle]: Handle] RETURNS [out:
ReadOnlyHandle]:
ProcY:
|
|
-- invalid
assignments ProcX ProcY: ProcX
|
ProcZ: ProcY f ProcZ:
|
In deterinining, the conformance of
two procedure types, any default specifications are ignored. Thus
it is possible to assign a procedure value to a procedure variable with
differently specified defaults. In a procedure call, the type of the
variable appearing in the call. not the declaration of the
actual procedure, determines the treatment of defaults. Thus the initializing
declarations in the following example are valid. Note that the declaration of 1'roc2 declares a procedure
constant that is indistinguishable from Prod except
for the default value of its argument.
Which: TYPE = {prod,
proc2. proc3}: Procl: PROCEDURE [p: Which <- procl] =
BEGIN
' •
•
END;
Proc2: PROCEDURE [p: Which 4- proc2] = Procl; Proc3: PROCEDURE [p: Which] +- Procl:
-- some calls
Procl[]; -- equivalent to Procl [prod]
Proc2[ ]; -- equivalent to Procl [proc2]
Proc3[proc3]; -- note that Proc3[] is not legal
5.2. Procedure calls
The syntax for calling a procedure is
CallStmt = Variable I Call
Call = Variable [
ComponentList ] I
where the Variable has some procedure type. Other forms of can
are discussed in
chapter 8. These specify "catch phrases" for
dealing with sienals (or errors)
that are generated because of the call.
ParameterLists and ResultLists are
FieldLists (section 3.4.1). In a call of a procedure, the arguments
are packaged into a record. Therefore, a procedure call may use all the syntax
for record constructors in passing arguments. Components (arguments)
may be specified using either keyword or positional notation:
arguments not explicitly specified may be supplied by default. The following calls
of Gcd are equivalent:
Gcd[x+ 1, y] Gcd[tn: x+ 1, n: y] Gcd[n:
y. nt: x+1]
If the ReturnsClause in a Procedu reTC is
not empty, then its ResultList specifies the number and
types of the results returned by a procedure of that type. It may be a named or
an unnamed FieldList (section 5.3.1 on the RETURN statement.
discusses how it is used).
Procedures that return results must be called from within Expressions
that use the results in some way. Such function references are
valid Expressions. Procedures that do not return results are used
in call statements. A procedure that does not return results is called by
simply writing a
CallStmt as
a statement by itself. For
example,
group: ARRAY [1..N] OF
POINTER TO Person;
Younger: PROCEDURE [first, second: CARDINAL] RETURNS [BOOLEAN] = BEGIN RETURN [group[firsaage< group[second].age]] END;
Exchange: PROCEDURE [first,
second: CARDINAL]
=
BEGIN
r POINTER TO Person;
t group[first]; group[first] group[second];
group[second] t
END;
Sort[first: 1, last: N, lessThan: Younger, swap: Exchange];
A call statement is ordinarily used to obtain side effects. Most often. these
take the form of changes to variables that are not local to the invoked
procedure, but they may also involve input or output. A
function may also have side effects as well as return results. On occasion,
only the side effects are important. and the user wishes to ignore the
returned results. An easy way to do this is to assign the result
record to an empty extractor:
--
call F and
discard its result record.
A
call that supplies no arguments is
written with an empty constructor. "[ I". When such a call is itself
a statement, the empty brackets may be omitted.
A
fine point:
When the call is used as an expression,
the empty brackets are mandatory: otherwise. the value of the expression is the
value of the procedure, not the value of its results. For example, consider the
two procedure variables in the following:
Procl: PROCEDURE RETURNS [INTEGER]: Proc2: PROCEDURE
RETURNS [INTEGER]:
-- here the program assigns values
to the procedure variables
IF Procl = Proc2 THEN ... -- compare the
procedure variables
IF Proc1[]= Proc2H THEN... -- compare their results
(integers)
At the time a call occurs, a specific activation is executing. the caller's activation. The effect of a
call is to suspend execution of the caller, to create a new
activation of the called procedure (including new storage for all
parameters and local variables), and to begin execution of that activation. An important
consequence of this structuring of procedure control is that all Mesa
procedures are inherently capable of being recursive and reentrant.
5.2.1. Arguments
and parameters
Arguments are values supplied at call-time: parameters are
variables that are local to a given activation. The association
of arguments with their parameters amounts to assignment, much as if the
following were written:
InRec: RECORD [argl: Typel. arg2: Type2, ...]: InRec 4- [argl: call, arg2:
val2....]: -- in
the caller
paraml:
Type]: param2: Type2:
[patwnl,
param2, ... ] InRec: --
in the called procedure
This is not just an idle analogy. The
semantics of assignment accurately describe how arguments are associated with
parameters. The
following are direct consequences of this:
An argument of a procedure need only conform to its parameter, just as
for assignment.
All arguments are passed by
value in Mesa: i.e., the value of
an argument, not its address, is assigned
to the parameter. Of course, this value itself can be an address
(e.g., if Typel were
POINTER TO TypeX).
5.2.2. Termination
and results
A procedure terminates by executing a RETURN statement,
which constructs a (perhaps empty) result record. The return operation then terminates
execution of the current procedure activation and
restarts
the caller from the point at which it vas suspended by the call. As part of the
return. storage for the parameters and local variables of the
returning procedure is released.
Since the value of a procedure is its result record, the
components of that record can be assigned to variables using an
extractor: alternatively. any single component (if named) can be referenced by
a field selector. The procedure ReturnExample
returns three integer results and may be used as indicated:
ReturnExample:
PROCEDURE
[option: [1..4]] RETURNS [a, b. c: INTEGER] = BEGIN ... -- body
defined in section 5.3.1 ... END:
X. y. z: INTEGER:
case: [1..4];
x +- ReturnExample[case].a; --
get a component
only
[b: y, c: z] ReturnExample[case]: --
assign results by extractor
x (ReturnExanzple[case].c+ 1) MOD 10; -- use c component
If a procedure returns an empty result record. the call
does not have a value and can only be used as a statement.
If a procedure returns a single-component result
record, extraction and selection are valid. In addition, the
component may be (and usually is) accessed directly because of the automatic
coercion from a single-component record to its single component. In
the following example, the first two
calls of Gcd are
valid and equivalent;
the third illustrates typical use within an expression:
gcd 4-
Gcd[m, n]: --
(coercion)
[gcd] 4- Gcd[m,
n]; --
(explicit extraction)
relPrime Gcd[m, n] = 1; -- (coercion)
Some
fine points:
In the declaration of ReturnExample. [a. b. c: INTEGER] defines a
unique type for the result record. Because of the conformance rule for record types
(section 3.3.2), it is impossible to declare a variable with that type. If a procedure is to
return a record value with a particular type T. it must return a single-component record where that component is a
record of type T.
For similar
reasons, the result record of G below is
not acceptable as the argument record of F.
F:
PROCEDURE [x. y: INTEGER]:
G: PROCEDURE [i: INTEGER] RETURNS [x. j: INTEGER]:
With these declarations, the call FIGIAJ is not
legal: it would be with the following declarations:
T: TYPE = RECORD [x.
y: INTEGER]:
F: PROCEDURE [in: n:
G:
PROCEDURE [i: INTEGER] RETURNS [out: T]:
5.3. Procedure bodies
An actual procedure declaration looks like the declaration
of a procedure variable followed by a special kind of =
initialization, a ProcedureBody. The TypeSpecification appearing
in the declaration determines the type of the body as well as
that of the procedure identifier. It may be any TypeSpecification equivalent
to a ProcedureTC. ProcedureBody is a special form of initialization
defined as follows:
Initialization = ...1 = ProcedureBody I 4- ProcedureBody
ProcedureBody = InlineOption
Block -- see section
4.4
for Block
InlineOption = empty I INLINE
If
the attribute INLINE appears.
the procedure body is an inline one:
any call of the procedure is replaced by a modified copy
of the body (section 5.6).
Only a procedure initialized with = to a ProcedureBody is called
an actual procedure: its
meaning
cannot change because it cannot be assigned to. If, however,
it is initialized to a
ProcedureBody using 4-
initialization, its value can be changed by assignment, and it is
considered a procedure variable. Initialization using 4-
is not permitted for an inline procedure.
In addition to other statement forms, a
procedure body can contain RETURN statements (described in the next section).
There is an implicit RETURN
at the end of each procedure body if one does not appear explicitly.
A ProcedureBody defines a scope for declarations; i.e.,
identifiers declared within it are local to the procedure and
are unknown outside it. There must be no duplicates among the names in -a
procedure's ParameterList, ResultList and local
variables. Names in the ParameterList can be used to write a
keyword constructor (section 3.3.4) in a call of a procedure. Similarly, names
in the ResuitList can be used in keyword extractors
(section 3.3.5) and as qualifiers (section 3.3.3)- to access
the results returned by a procedure. Within a procedure, any named fields of
parameter and result records act just as local variables; the
former are initialized with the values of the actual parameters.
A ParameterList for an actual procedure should be a named field list so that the procedure
body can reference the parameters.
A fine
point:
Although the parameters and results act
as local variables within the block that is the procedure body, the
scopes are slightly different. The scope
of the named parameters and results includes any OpenClause. EnableClause or ExitsClause of that block: the scope of the local variables does not
(section 4.4.2).
5.3.1. RETURN statements
There are two basic forms of RETURN statement:
RETURN and
RETURN followed
by a constructor. When either form is executed. control returns to
the point from which the procedure was called. In addition,
the RETURN can
supply results in the form of a constructor conforming to the type of the procedure's
ResuitList:
ReturnStmt ::= RETURN I RETURN [ ComponentList
There may be any number of RETURN statements
in a procedure body. The form of a RETURN statement depends
upon the ReturnsClause in the definition of the procedure type. There
are three cases to be considered:
no ReturnsClause (empty
result record) an unnamed
field list as the ResuitList a
named field
list as the ResuitList
If there is no
ReturnsClause, the ReturnStmt must
be just "RETURN".
An explicit RETURN statement can be omitted at
the end of the procedure in this
case.
If an unnamed field
list is used for the ResultList, each ReturnStmt must include a
positional constructor. That constructor must match the field list
exactly, with one component for every field (omission, elision and voiding are not allowed). In
this case, there is no implied return at the end of the
procedure.
If the ResuitList is a named field list, either form of ReturnStmt
is acceptable. If no explicit constructor appears, the current values of
the named result variables define the value of the result record.
An explicit constructor may use either positional or keyword notation; again,
omission, elision and voiding are disallowed. A RETURN statement
is optional at the end of the procedure; if omitted, an
implicit RETURN of
the result variables is provided. An example follows:
|
ReturnExample: PROCEDURE [option: [l..4]] RETURNS [a, b. c: INTEGER] =
BEGIN
a4-134-
SELECT option
FROM
|
|
1 = >RETURN
|
a: 1.
|
|
2, c: 31;
|
-- keyword parameter list
|
|
2 = > RETURN 3 = > RETURN;
|
[ 1. 21,
|
31b:;
|
|
-- positional version of option 1 a=b=c=0
|
|
ENDCASE => b4-4:
|
|
|
|
|
c4-9;
|
|
|
|
|
END:
|
|
|
-- implicit return: a= O. b=4. c=9
|
5.4. A package of procedures
This section contains an example of a simple module, Binary Tree, which is designed
to create and manage a data base structured as a binary tree.
It is typical of the ways in which related procedures are
packaged together. The example illustrates many of the issues discussed in the
previous sections and also introduces the use of modules and
interfaces in Mesa.
The binary tree implemented by the example is a data
structure containing nodes linked by pointers. Any node points to at most two
others (its sons), and
a node is pointed to by exactly one other node (its parent). A special root node exists and is
referenced by a pointer not in the tree. Every node also
contains a value, which
for simplicity in the example is just an INTEGER. When the program starts,
the tree is empty, and any call to Seek
Value will return a count of zero.
The nodes in this particular binary tree are records
with four components:
value an
integer value (with unspecified interpretation),
count the
number of duplications of the value in the data base,
left pointer
to a "left" son node (or NIL), and
right pointer
to a "right" son node (or NIL).
There are rules of association between the
values and the nodes: The first supplied value is entered into the
root node.
A given value may exist in only one node; duplications
are counted.
If node E points to "left" son L. then all the
values in the subtree rooted at L are less than the value in E. If node E points to
"right" son G, then the values in the subtree rooted at G are greater
than the
value in E.
When the module is started, the tree is initialized to be
empty. Thereafter, the module itself executes no code, but its
procedures can be called to alter the tree that it manages. For instance, other
modules call PutNewValue to
insert new values into the tree.
PutNewValue calls
another of BinatyTree's procedures,
FindValue, which
traverses the tree seeking a node that already has a
given value. Find Value may
find such a node, or it may fail by reaching a higher-valued node
with a NIL left
son or a lower-valued node with a NIL right son. If Find Value finds a node with the given value, PutNewValue increments that
node's count. Otherwise,
PutNewValue sets
up a new node and attaches it to the node returned by Find Value.
This strategy is chosen for simplicity, but it can be a
poor way to construct a binary tree. For instance, if the values are
entered in strictly decreasing order, the tree becomes a linear list of left nodes.
To find the lowest-valued node, every
node must be examined.
The reader should read the
explanation following the example in conjunction with the example itself.
Fxample
2. A Package of Procedures
1:
DIRECTORY
2:
Storage:
FROM "storage"
USING [Allocate].
3:
OrderedTable:
FROM "orderedtable"
USING [UserProc];
4:
5:
BinalyTree:
PROGRAM IMPORTS Storage EXPORTS OrderedTable
=
6:
BEGIN
7:
8: --
type definitions and compile-time constants
9:
Node: TYPE = POINTER TO BinaryNode;
10:
BMaryN
ode: TYPE = RECORD
[value: INTEGER, count: CARDINAL, left.
right: Node];
11:
nodeSize:
CARDINAL = sIzE[BinatyNode];
12:
13: --
a global variable
14:
root: Node:
15:
16: --
public (exported) procedures:
17:
SeekValue:
PUBLIC PROCEDURE [val: INTEGER] RETURNS [count: CARDINAL]
=
18:
BEGIN
19:
node: Node;
20:
found: BOOLEAN;
21:
[found,
node] 4- FindValue[val]; -- see
if it is in the tree
22:
RETURN [IF found THEN node.count ELSE 0]
23:
END;
24:
25:
PutNewValue:
PUBLIC PROCEDURE [val: INTEGER] =
26:
BEGIN
27:
node,
nextNode: Node;
28:
alreadyInTree:
BOOLEAN;
29:
-- Use FindValue to find where to
put val:
30:
[alreadyInTree, node] 4- FindValue[val]:
31:
IF alreadyInTree THEN node.count node.count+ 1
32:
ELSE BEGIN -- name "external" procedure Allocate by qualification
33:
nextNode
4- Storage. Allocate[nodeSize];
34:
nexiNodet
BinaryNode[val, 1, NIL, NIL]; -- initialize the new node
35:
IF root=
NIL
THEN root nextNode
36:
ELSE IF vaKnode.ialue THEN node.left 4- nextNode ELSE node. right t nextNode;
37:
END;
38:
END;
39:
40:
EnumerateValues: PUBLIC PROCEDURE [userProc:
OrderedTable.UserProc] =
41:
BEGIN
42:
-- a local procedure (sec. 5.6)
43:
Walk: PROCEDURE [node: Node] RETURNS [keepGoing:
BOOLEAN] =
44:
BEGIN -- walk through the tree in order by increasing
value using recursion
45:
RETURN [node = NIL --
don't examine empty (sub)trees
46:
OR (
47:
Walk[node.lefi] --
enumerate the lesser-valued nodes first
48:
AND userProc[node.value, node.count] --
enumerate this node
49:
AND Walk[node.right] --
then enumerate the greater-valued nodes
50:
)]
51:
END; -- of Walk
52:
Walk[root]; --
just start enumerating at the root
53: END;
54: --
a procedure that is private to this module
55:
FindValue:
PROCEDURE ral: INTEGER] RETURNS [ inTree: BOOLEAN,
node: Node] =
56:
BEGIN
57:
nexiNode:
Node root: -- always
start at the root
58:
IF root= NIL THEN RETURN [FALSE. NIL];
59:
UNTIL nextNode=
NIL
60:
DO
61:
node 4-
nextNode:
62:
nextNode
4- SELECT val FROM
63:
< node. value =>
node.lefi.
64:
> node. value =>
node. right,
65:
ENDCASE =>
NIL;
66:
ENDLOOP;
67:
RETURN [val= node. value, node]
END:
68:
69:
70: --
mainline statements
71:
root 4-
NIL; --
make tree initially empty
72: END.
5.4.1. The
example
Each
line of the source code in Example 2 is numbered for convenient reference;
other than that, the code could be compiled as it stands.
The body of a PROGRAM module resembles a procedure
body: BEGIN, followed
by declarations, then some statements, and finally END. The declarations
and statements are both optional, but it would be unusual to omit the declarations.
In this example, the module BinagTree declares five actual
procedures: Seek Value (lines
17-23), PutNewValue (lines
25-38). EnumerateValues (lines
40-53), Walk (lines
43-51) and FindValue (lines
55-68). It also declares two types (Node and BinagNode),
a constant (nodeSize).
and a single global
variable
(root). The
scope of these declarations is the entire body of the module (lines 6-72). For
example, PutNewValue,
EnumerateValues and FindValue
all reference the global variable root.
When a module is created and started (chapter 7), the
global variables are created and any statements in its body are
executed. Binary Tree has
just one such statement (line 71). which creates the initial empty
tree by assigning NIL
to root. Storage
for activations of modules is not released when control
reaches the end of the main body. Global variables such as root continue to exist and
may be
used to retain data shared by the
actual procedures
in the module.
The procedure EnumerateValues has two major distinguishing features:
it takes a procedure value as a parameter. and it contains
the declaration of a nested procedure (Walk). For each node in the tree,
EnumerateValues calls
the procedure value userProc that
it received as an argument. passing it the value in that node and its
replication count. If userProc returns
TRUE, the
enumeration of the values continues; if it returns FALSE, EnumerateValues terminates and
returns to its caller. The values are generated in order from least to greatest.
The nested procedure Walk is recursive and traverses the tree by first
traversing the left subtree, then visiting the
root, and finally traversing the right subtree. This postorder traversal
delivers the values in increasing order (the reader should
convince himself that it does). The expression in lines 47-50
depends upon the definitions of AND and OR (section 2.5.3) to terminate the traversal as soon as
userProc returns
FALSE. The
first procedure call occurs only if node
is not NULL; the second only if the first is
called and returns TRUE;
the third only if the first and second are called and both
return TRUE. Section
5.6 treats local procedures in more detail.
5.4.2. Invoking
procedures in other modules
The DIRECTORY section at the beginning of
a module associates identifiers with file names. The identifier Storage. for example, must be the
name of a (DEFINITIONS)
module that is stored on the file
named "storage". Such modules allow the independent development of
interface definitions and the sharing of such definitions. Storage and OrderedTable are said to be included by BinalyTree. The optional USING clause
provides compiler-checked documentation of exactly which identifiers are used in a module but defined in the
associated interface.
The IMPORTS list (section 7.4.1) on line 5 allows Binatyrree to access a
procedure (Allocate) defined
in the interface
Storage, which
has the following (skeletal) form:
Storage: DEFINITIONS = BEGIN
• • •
Allocate: PROCEDURE [size: CARDINAL] RETURNS [POINTER TO
UNSPECIFIED]: . . .
END.
The
example uses explicit qualification (dot notation) to name the Allocate procedure (line 33). The
EXPORTS
list (section 7.4.3) names the single interface OrderedTable, which is defined as
follows:
OrderedTable: DEFINITIONS = BEGIN
-- types
UserProc: TYPE = PROCEDURE [val: INTEGER.
count: CARDINAL] RETURNS [continue: BOOLEAN]; -- the interface
Seek Value: PROCEDURE [val: INTEGER] RETURNS [count: CARDINAL];
PutNewValue: PROCEDURE [val: INTEGER];
EnumerateValues: PROCEDURE [userProc: UserProc]:
END.
Other modules access the PUBLIC procedures in BinaryTree (Seek Value, PutNewValue and
Enumerate Values) by
importing this interface (just as BinaryTree
imports Storage):
they have no other access to BinaryTree. For example, Find Value is private to BinaryTree.
so it is only called
from within the module (lines 21 and 30). The definition of the type UserProc is included in the
interface so that it is publicly available for defining
procedures to be passed to EnumerateValues.
Note that BinaryTree also obtains the definition of this type from
the interface (line 40).
5.5. Nested procedures
Actual procedures may be declared within procedure bodies.
A nested procedure is
one declared within (and local to) some enclosing procedure.
Nesting of procedure declarations restricts the scope of
the names of the inner procedures. In addition, the enclosing procedure
establishes an environment for the inner; this is especially useful when the
inner procedure is passed as a parameter.
The value of a nested procedure (and any activation of
that value) is ''tied" to the local variables of the enclosing procedure
and, indirectly, to the local variables of the procedure or module in which the
enclosing one is declared, etc. An activation of the nested procedure
references those variables available at its point of declaration. A
different activation of the enclosing procedure declares a nested
procedure with a different value.
one with its nonlocal variables tied to that other instance of the
enclosing procedure.
|
Mesa Language Manual
The following example uses the interface OrderedTable defined in
section 5.4 and illustrates application of a nested
procedure.
ArerageValue: PROCEDURE RETURNS [INTEGER] = BEGIN
sun?.
n: INTEGER:
Add Value:
OrderedTable.UserProc = -- a nested procedure
BEGIN
1?
n + count: SUM 4- sum + count*val: RETURN [continue: TRUE]
END;
sum 4- n 4-
0:
OrderedTable.Enumerateralues[AddValud
RETURN [IF n= 0 THEN 0 ELSE (IF sum<0 THEN sum —
(n/2) ELSE sun? + ( n/2))/ END;
|
79
a typical
|
The procedure AverageValue
computes the average value of the value fields in the binary tree.
It declares and initializes a pair of local variables (n and sum) that are updated by the
nested procedure AddValue but
must have a greater lifetime than any individual activation of Add Value. Note that a similar
effect could be achieved by making n
and sum global
variables in this case: the suggested solution restricts their
scope (and thus the opportunity for accidental misuse).
Execution of AverageValue
involves a second nested procedure, the procedure Walk within Enumerate Values. The
latter's parameter userProc serves
a purpose similar to that of sum or
n in
Average Value. Since
there is nothing to prevent a recursive call of Enumerate Values from some actual procedure
corresponding to userProc, making
userProc a
global variable in the module BinaryTree
could be disastrous.
A fine
point:
Because a nested
procedure is tied to an activation of the enclosing procedure (even when it
references no nonlocal
variables), the value of a nested procedure should not be assiened to a
variable with a lifetime greater than that of the enclosing procedure instance.
In a sense, all procedures are "local"
procedures. They are either local to some enclosing procedure or local to some
module (recall that static variables are local to the module declaring them).
This nesting can continue to an arbitrary number of levels.
(The level is important only to the extent that it influences
name scopes, a topic covered in the next section.)
5.5.1. Scopes defined by procedures
Each
procedure body defines a new scope for names declared in that procedure. Such
names represent variables that are local to the body. The scope
for a local variable is such that:
(1) the
local variable is unknown outside of
that procedure body, and
(2) a
non-local variable is unknown inside
the procedure if its name matches some local variable's name.
Within
a procedure body, a block (section 4.4) can be used to further restrict the
scope of a local variable. In the following example, scopes for the procedures
are indicated by comments:
Soindlodule: PROGRAM =
BEGIN
var. INTEGER:
-- the var Of INTEGER type is used here OuterProc:
PROCEDURE
=
BEGIN
var: BOOLEAN:
. -- the var Of BOOLEAN type
is used here
Local Proc: PROCEDURE =
BEGIN
var. CHARACTER:
--
the var Of CHARACTER type
is used here
END:
. . . --
the var of
BOOLEAN type
is used here
END:
--
the var of INTEGER type
is used here
END.
5.6. Inline
procedures *
An
actual procedure is said to be inline
if the attribute INLINE appears before the body in
the declaration of that procedure. Any call of the procedure
is replaced by an inline expansion,
which is
a modified copy of
the procedure's body. The code of the procedure and any storage required for
local variables are merged with the code and storage of
the calling procedure or module. Thus inline procedures can be
used to eliminate the overhead of a procedure call and return (usually at
the cost of a longer object program).
The rules for creating the expansion are defined so that
the presence or absence of the INLINE attribute has no effect upon the meaning of a
program. Execution of the expansion must always produce a result
with the same logical behavior as the result of applying the following
operations:
(1) For
each argument, create a uniquely named variable local to the caller, and
initialize that variable with the value of the argument.
(2) If
there is a result record with named fields, enclose the body of the inline
procedure in a block containing a declaration of each such
field.
(3) In the resulting block, replace each
reference to a field of the parameter list by the identifier introduced in the
first step for
the corresponding argument.
Any global variables of the procedure body refer to the
corresponding variables accessible at its point of declaration, not the point of call.
Some fine points:
A catch phrase can be attached to
the call of an inline procedure (section 8.2.1). The arguments are evaluated outside the scope of the catch
phrase.
The Mesa compiler
attempts to discover many of the common cases in which "call by name"
is equivalent to the
"call by value" substitution described above. When it discovers such
a case, the argument is substituted directly for the corresponding parameter.
The attribute INLINE is never mandatory. Deleting
INLINE is
always valid, but adding it is not. No inline procedure can be recursive,
either directly or indirectly through a chain of inline procedure calls.
Consider a procedure Proc declared
as follows:
Proc: PROCEDURE [v:
INTEGER] RETURNS [INTEGER] = INLINE BEGIN
RETURN [v*I' + 3*v + 1]
END:
Because of its INLINE attribute, Proc cannot be used in any of
the following situations:
When Proc itself
is the operand of one of the fundamental operations of assignment (procVar Prue, GeneratorProc[Proc]. etc.)
or comparison (Proc = AnotherProc).
When Proc itself
is used as an alternative in a conditional expression, e.g..
(IF predicate
THEN Proc ELSE AttotherProc)lxj.
When Proc is
the operand of FORK (section 10.1).
When Proc is
to be exported to an interface (section 7.4.3).
Some
line points:
Since arguments are evaluated
before procedures are called. usage such as Proc[Proc[x]] does not make Proc
recursive.
Additional restrictions appl3 when an
inline procedure is declared in a DEFINITIONS module (see section 7.3.3).
CHAPTER 6.
STRINGS, ARRAY
DESCRIPTORS,
RELATIVE POINTERS, AND VARIANT RECORDS
This
chapter introduces two new data types. strings and array descriptors, discusses
relative pointers, and also extends the definition of record types
to include variant records.
In Mesa, the type STRING is really "POINTER TO StringBody"; a
StringBody contains a length
field indicating how long the string currently is. a maxlenglh field giving the length of
that array, and a packed array of characters.
An array descriptor describes the location and
length of an array. For ordinary arrays. these are fixed
at compile-time. Values of array descriptor type. however, have location and length items that can
vary. These array descriptors may represent arrays that are dynamic. but they
may also represent ordinary arrays. For efficiency, users often
pass array descriptors to procedures instead of passing the entire arrays
themselves.
Relative
pointers require the addition of a base pointer
to obtain an absolute pointer. This allows data structures
with internal references that are independent of memory location.
Variant records contain a set of common fields and a
variant portion with a specified set of different possible
interpretations.
6.1. Strings
In Mesa, a string represents a finite, possibly empty,
sequence of characters. Associated with a string are the following:
length the
number of characters represented. The length may vary at run-time (except
for constant strings).
maxlength the
maximum length. This guarantees that the string is finite. A string's length
may vary from zero up to its maximum length.
text an
indexable sequence of characters.
STRING
is a predefined type in Mesa. Each program contains the
following relevent pre-declarations:
STRING: TYPE = POINTER TO StringBody;
StringBody: TYPE = MACHINE DEPENDENT RECORD [ length: CARDINAL,
maxlenglh: --read
only-- CARDINAL,
text: PACKED ARRAY
[0..0) OF CHARACTER]:
Suppose s is a STRING nariable.
Then s.length and
s.maxlengrh refer
to the first two components of the string structure
currently pointed to by s. The
type StringBody is
"built into" the Mesa language so that the ith character of
the text array,
sdext [l], may
he abbreviated s[1]. The index type of text in the declaration is used only to specify a
starting index of 0. It is better to think of a particular STRING as
having an index type [0..s.maxlength).
The value of s.maxlength
is assigned when a string structure is created and is a
constant: it may not appear as a LeftSide in the user's program. However.
s.length can
be used as a LeftSide. In fact, the user is responsible for
setting and changing the length when appropriate (i.e.. s.length is meant to reflect
the "meaningful" length of the character sequence). Suppose. for
instance, that s initially
points to an empty string. Then the user might append
characters as follows:
s[s.length] anotherChar
s.length 4- s.length+1;
Actually, characters are seldom appended in this manner. The recommended practice is to use string-handling
procedures provided by the Mesa system. These are
documented in the Mesa System
Documentation and in appendix C of this manual.
Since strings in Mesa are actually pointers to string
bodies, several strings may refer to the same body. Therefore, a change to that structure would
manifest itself in all such strings. Keep the following in mind:
When an item has type STRING, think "string-pointer".
A
fine point:
While the programmer cannot assign
to the maxlength field with an assianment statement. it can be set
(along with the
length) in a constructor, i.e.
AllocateWords: PROCEDURE [n: CARDINAL] RETURNS [POINTER TO
UNSPECIFIED]: s
STRING:
k: CARDINAL:
s F AllocateWords[StringDefs.WordsForString[k]]:
StringBody[length: 0. maxlength: k. text: ]:
This is the way to
initialize a StringBody when the space for it comes from
some general storage allocator. Note that the text field cannot be set with the
constructor since the ARRAY is of length zero in the declaration.
6.1.1. String literals and string Expressions
String literals are written by enclosing the desired
sequence of characters in quotation marks, "...". A
quotation mark within a string constant is represented by a pair of quotation
marks (""). Here are some examples of string literals:
"The first example contains
some embedded carriage-returns."
"A quote mark (') isn't a quotation
mark('")..."
-- an empty string
A
string literal is an Expression of type STRING. Its value is a constant pointer to a constant StringBody
in which:
length = number
of characters given, and
maxlength = length
The fundamental operations arc defined for string Expressions.
They deal with them as pointer values: e.g.. assigns one string pointer to
another string
pointer. = compares two strings for the
same pointer value,
and # compares two
strings for different pointer values.
A
fine point:
The body of a string
literal is ordinarily placed in the global frame of the module in which the
literal appears lit is copied from the code when the module is STARTed).
Pointers to that body (the actual STRING values) can then be used freely with little danger that the
body will mote or be destroyed. Unfortunately. this scheme can consume substantial amounts of
space in the (permanent and unmox able) global frame area.
If
a string literal is followed by 'L (e.g.. "abc"L). a copy of the
string body is moved from the code to the local frame of the smallest enclosing procedure whenexer
an instance of that procedure is created. As a corollary. the space is freed and the string body
disappears when the procedure returns. This allows smaller global frames. but it is important to insure that
pointers to local string literals are not assigned to STRING
variables with lifetimes
longer than that of the procedure. Programmers should avoid using
local string literals until performance tuning is necessary (except perhaps in calls of
straightforward output procedures).
6.1.2. Declaring
strings
String variables are declared like ordinary variables, but
there is one additional form of initialization (for strings only):
Initialization = 4- [
Expression ] I = [ Expression ]
The Expression must be a compile-time constant Expression
of type CARDINAL.
At run-time, Mesa creates a string
structure with tnaxlength equal
to this Expression's value, length
equal to zero, and text uninitialized. The declared string variable is
then set to point to this string structure. If an IdList is declared
with this form of initialization, all of the listed variables initially point
to the same string structure.
Some examples:
currentLine: STRING 4-
[256];
stringBuffer: STRING +- [stringAfax+someExtra];
This would cause allocation of two string
structures in the frame of the program or procedure containing
the declarations. The string currentLine
would point to one whose maxlength is 256. The
string stringBuffer points
to the other string structure. (Note that stringitlax and someExtra
must be compile-time constants.) Since the initialization
is done with "4-",
it is legal to assign new pointer values to these string variables.
The following are examples of fixed form string initialization:
what WasThar• STRING =
"Eh?":
goofed: STRING = whatWasThat:
In this case, Mesa would allocate and fill in a string
structure for string constant "Eh?". whatWasThat and goofed, would be compile-time
constants having the same string value: i.e.. they would
both point to the same string structure. In fact, any other references to the
same string literal
will point to the
same string structure. For example:
huh: STRING =
"Eh?";
String variables
can be declared with initialization
or without any initialization:
stdErrorAlsg: STRING 4- "It
seems that we have made a mistake." firstReply, reply: STRING 4- "Yes";
oldBuffer, newBuffer: STRING:
IF quickDialog THEN siciErrorMsg, F whatli.ctsTnat:
IF reply [0] = .? THEN
IF firstReply [01= "? THEN HelpaLot ELSE
HeIpaLittle:
old13uffer.- newBuffer
s-tringllufferl:
. .
IF stringBufferl#stringBuffer2 THEN newBuffer.- stringlluffer2:
A fine
point:
The
Mesa system contains procedures you should use when allocating blocks of data.
These procedures are helpful
for applications involving an arbitrary number of strings or strings of
arbitrary length. The procedures are documented in the Mesa
System Documentation.
6.1.3. Long
strings *
A STRING is
just a pointer, so
LONG
STRING is also a predefined type:
LONG STRING: TYPE = LONG
POINTER TO StringBody;
It
is perhaps curious to note that declaring a LONG string says nothing about its actual or potential
length.
6.2. Array descriptors
A full description of an array contains several items of
information. Consider a typical array declaration:
schedule: ARRAY [1..999] OF Date:
The following things are known about schedule:
base = gschedule[1],
Index type = [1..999] (a
subrange of INTEGER Or
CARDINAL), minIndex = 1.
length = 999.
component type
= Dale
All of these items except base are compile time constants.
and the value of base is
the address of a fixed place in the frame, chosen by the compiler. Mesa
provides a mechanism for dynamic arrays, where the base and length can vary at run-time. The
implementation does not allow for a variable minlndex. Dynamic arrays are implemented by means of Array descriptors.
6.1.1. Array
descriptor types
An array
descriptor type is constructed much like an array type:
DescriptorTC = DESCRIPTOR FOR ReadOnlyOption A rrayTC
DESCRIPTOR FOR ReadOnlyOption PackingOption ARRAY OF
TypeSpecification
ReadOnlyOption = empty I READONLY
PackingOption :: = empty I PACKED
For example,
events: DESCRIPTOR FOR
ARRAY [1..999] OF Date:
If
READONLY is
specified, the contents of the array cannot be changed via the descriptor. In
the second form (where no IndexType is given) the
index type is an integer
subrange starting at zero.
A value for events is an array descriptor (a record-like object
containing items similar to those described previously for schedule except that the base is not fixed). The next
declaration specifies an array descriptor in which the base and the length are
variable:
hisuny: DESCRIPTOR FOR ARRAY OF Date:
Indexing can be used to access components of events and history as if they were actual arrays
instead of array descriptors (see sec. 3.2.1). Since no index type is specified
for history, it
has an indefinite index type starting
at zero with no specified upper bound.
Two array descriptor types are equivalent if they specify
equivalent types for their array elements and if they have equivalent
index-sets (or if both index-sets are unspecified). Note that DESCRIPTOR FOR ARRAY [0..2] OF T
and DESCRIPTOR FOR
ARRAY [1..3] OF T are different types, even though the lengths
and element types are the same. Expressions of equivalent descriptor
types may be compared for equality (= or #).
The rules for assignment are somewhat more relaxed. If al has type DESCRIPTOR FOR ARRAY OF T. and a2 has type DESCRIPTOR FOR ARRAY [0..10) OF T, then the assignment al 4- a2 is
legal, but the assignment a2 4- al is not.
In any case, for assignments and comparisons,
both operands must be array descriptors, and it is the descriptors
themselves, not the
arrays that they describe which are the values operated on. It would be
an error to attempt to assign
events to
schedule because
the first is a descriptor and the second is an actual array.
There are three function-like operators relevant to array
descriptors: DESCRIPTOR,
BASE, and LENGTH. DESCRIPTOR
returns an array descriptor result and has three distinct
forms which are treated syntactically as built in functions:
BuiltinCall = DESCRIPTOR [ Expression
]
DESCRIPTOR [ Expression
, Expression ]
DESCRIPTOR
[ Expression , Expression , TypeSpecification
BASE [ Expression I
LENGTH [ Expression I
The first form takes an argument of some array type: e.g.,
events 4- DEscw-roR[scheduk];
The result is an array descriptor for schedule. The
second form needs two arguments:
base: POINTER TO UNSPECIFIED -- address of the minIndex component
length: CARDINAL --
number of components
This form may only be assigned to an array descriptor
variable which was declared without an explicit index type.
In those rare situations
where the compiler cannot deduce the component type of the descriptor from
context a form of the DESCRIPTOR
construct is provided which takes three arguments. The third
one is a TypeSpecification, the component type.
The following example provides a fresh array of
64 Dates:
Allocate: PROCEDURE
[blkSize: CARDINAL]
RETURNS [POINTER TO UNSPECIFIED]; history
<- DESCR IPTOR[ Allocate [64*sizE[Daie]l.
64];
The
expressions BASE[] and
LENGTH[] take
one argument (of array descriptor or array type). BASE yields the base of
the described array. and LENGTH yields
its length. For example:
events DEscRiProR[schedule]: --
describe the entire array
events DEscRiProR[BASE[schedule]. 5]: -- describe the
first 5 elements
There is no special form for constructing, DESCRIPTORS for
packed arrays. The PACKED
attribute is deduced from context. In the two or three
argument form of DESCRIPTOR
for packed arrays, the second argument
(the LENGTH) is
the number of elements.
It is usually more efficient to pass array descriptors as
arguments, rather than arrays. Since arguments are passed by
value, an array argument causes a copy of the entire array to be made twice (once
to put it into an argument record, and once to copy it into a local variable in
the called procedure). The next example shows a case in which array descriptors must
be used, since passing by value would not work:
SortInPlace: PRocEDuRE[Tabie];
-- sorts in situ
Table: TYPE = DESCRIPTOR FOR ARRAY OF
INTEGER; thisArray: ARRAY [0.. this) OF INTEGER;
ihatArray: ARRAY [0..that)
OF INTEGER;
anyTable: Table 4- DESCRIPTOR[ihisA rray];
SortInPlacetaityTablel: --
sorts thisArray
SortInPlace[DEscRIPToR[thatArray]]; -- sorts thatArray
A StringBody (sec. 6.1)
contains an array, text, of
characters. One must be careful when constructing a
DESCRIPTOR for
this array. Recall that the bounds of text are [0..0). This declaration is used since
the
actual length of text varies from STRING to
STRING. For
this reason, the "one argument" form
should
not be used to construct
a DESCRIPTOR for text.
textarray: DESCRIPTOR FOR
PACKED ARRAY OF CHARACTER; s: STRING;
textarray +- DEscRiPToR[s.rext]: LENGTH[textarray] is
incorrect
textarray DESCRIPTOR[BASE[s. text], s.
length]: --
correct
6.1.2. Long descriptors *
The BASE portion
of an array descriptor is essentially a pointer. Just as the language allows
the type LONG
POINTER, it also allows the type LONG DESCRIPTOR. The syntax is
straightforward:
TypeConstructor = ... I LongTC
LongTC = LONG TypeSpecification
TypeSpecification = .. I DescriptorTC
All the standard operations on array descriptors
(indexing, assignments, testing equality, LENGTH, etc.) extend to long array descriptors. The type of BASE[desc]
is long if the type of desc is
long. The LENGTH of
an array descriptor is a CARDINAL. whether the descriptor (i.e. its BASE) is LONG or
short.
Long array descriptors are
created by applying DESCRIPTORH to an array that
is only accessible
 through
a long pointer, or by applying DESCRIPTOR[ ] or DESCRIPTOR[ ., ] to operands which is long.
Alternatively, when a short array descriptor is assigned to a long one, portion
is automatically lengthened. Consider the following examples:
through
a long pointer, or by applying DESCRIPTOR[ ] or DESCRIPTOR[ ., ] to operands which is long.
Alternatively, when a short array descriptor is assigned to a long one, portion
is automatically lengthened. Consider the following examples:
d: DESCRIPTOR FOR
ARRAY OF T;
dd: LONG DESCRIPTOR
FOR ARRAY OF T: ir: CARDINAL:
pp: LONG POINTER TO ARRAY [0..10) OF T:
dd 4- DESCRIPTOR[ppc]; --
descriptor for the entire array
dd 4- DESCRIPTOR[pp. 5]: -- descriptor
for half of the array
dd 4- d: --
automatic lengthening
pp 4- BAsE[dc4; -- BASE of
long is long
0 4- LENGTHIddi. --
LENGTH is always a CARDINAL
6.3. Base and relative pointers
Mesa
provides relative pointers, i.e., pointers that are relocated by adding some base value
before they are dereferenced. Relocation has the further effect of mapping a
value with some pointer type into a value with a possibly
different pointer type. Relative pointers are expected to be useful in such
applications as the following:
Conserving Storage. Relative
pointers can adequately identify objects stored within a zone of storage if the
base of that zone is known from context. If the zone is of known and relatively
small maximum size, fewer bits are needed to encode the relative pointers.
Since a relative pointer and the corresponding base value can have
different lengths, relative pointers can be shorter than
absolute pointers to the same objects. Overall storage savings are possible
when all the base values can be contained in a small number of variables shared
among many different object references.
Providing Movable Storage Zones. If
all interobject references within a storage zone are encoded
as zone-relative pointers, the zone itself can be organized to contain only
location-independent values. Moving the zone, possibly
via external storage, requires only that a set of base pointers
be updated.
Designating
Record Extensions. Sometimes it is convenient to extend a record by
appending information (especially variable-length information) to
it. Pointers stored in, and relative to the base of, the extended record
provide type-safe access to the extensions.
6.3.1. Syntax for base and relative pointers
The syntax for BASE and RELATIVE pointer type
constructors is as follows:
PointerTC ::= Ordered
BaseOption POINTER Optionallnterval PointerTail
BaseOption :: = empty I BASE
TypeConstructor ::= RelativeTC
RelativeTC ::=
Typeldentifier RELATIVE TypeSpecification
In a PointerTC,
a nonempty Optionallnterval declares a subrange of a pointer type,
the values of which are restricted to the indicated interval (and can
potentially be stored in smaller fields). Normally, such a subrange
type should be used only in constructing a relative pointer type as described below, since its values cannot span all of memory.
The BaseOption BASE
indicates that pointer values of that type can be used to
relocate relative pointers. Such values behave as ordinary pointers
in all other respects with one exception: subscript brackets
never force implicit dereferencing (see below). The attribute BASE is
ignored in determining the assignability of pointer types.
A RelativeTC constructs a relative pointer or
relative array descriptor type.
The Typeldentifier
must evaluate to some (possibly long) pointer type which
is the type of the base. and the TypeSpecification must evaluate to a (possibly long) pointer or array
descriptor type.
Relocation of a relative pointer is specified by
using subscript-like notation in which the type of the "array"
is the base type and that of the "index" is the relative pointer
type. Thus if base is
a base pointer and offset is a relative pointer (to 7). the form
base [offset]
denotes an expression of
type T, and
the value of that expression is (LOOPHOLE[base] + offset)r.
6.3.2. A relative pointer example
Consider the BinaryTree
example from section 5.5. In this program, an ordered
table is stored as a binary tree. The tree is stored in
the following Mesa data structure:
Node: TYPE = POINTER TO
BinaryNode:
BinaryNode: TYPE =
RECORD[value: INTEGER, count: CARDINAL, left, right: Node]:
Suppose that the BinaryNodes are allocated from a contiguous region of
memory. If the programmer now wishes to put the current state of
the ordered table on secondary storage, it is not sufficient
to simply write out the region of memory containing the BinatyNodes's. This is because the
data would make sense only if read back into exactly the same place in memory,
a restriction that is difficult to live with. The difficulty
stems from the absolute pointers used in the nodes. The problem
can be solved by changing the definition of Node. If the BinalyNode's are allocated from a region
of type TreeZone. let
TZHandle: TYPE = BASE
POINTER TO TreeZone:
Node: TYPE = TZHandle
RELATIVE
POINTER TO BinatyNode:
The
procedure Midi/aloe would
be written as follows:
NullNode: Node = <some
value never allocated>: tb: TZHandle;
root:
Node 4- NullNode: --
list is initially empty
Find Value: PROCEDURE [val: INTEGER] RETURNS [inTree: BOOLEAN,
node: Node] = BEGIN
nextNode: Node I- root:
IF root = NullNode THEN
RETURN [FALSE„VONOde]: UNTIL
nextNode= NullNode DO
node 4- nextNode:
nextNode 4- SELECT vat FROM
<
tb [node]. =>
tb[node].lefi,
>
tb [node].
value => tb[node].right,
ENDCASE
=> NullNode;
ENDLOOP;
RETURN[vai= tb [node]. node]:
END;
The other procedures of Rimy)'Tree can easily be rewritten to
use the new definition of Node. The
compiler would aid in the translation. since any
unrelocated dcreferencing of a Node
would be a compile-time error.
This new implementation of BinaryTree has the feature
that the TreeZone could
be moved around in memory, or written and read on secondary
storage, and only the base pointer tb
need be updated to reflect the new position of
the TreeZone.
6.3.3. Relative
pointer types
An
important topic to consider is the interaction of the relative pointer
constructs with the type machinery of Mesa.
A
RelativeTC constructs a relative pointer type whenever both the Typeldentifier
and the TypeSpecification evaluate
to pointer types. Let a RelativeTC be
Typeldentifier RELATIVE TypeSpecification,
where
Typeldentifier is of type
[LONG]
BASE POINTER [SubRangel)]
TO
[READONLY] Tb ,
TypeSpecification is of type
[LONG] [ORDERED] [BASE] POINTER [SubRanger] TO [READONLY] Tr ,
and
the brackets indicate optional attributes. Relative pointer values must be
relocated before they are dereferenced. If base and offset are base and relative
pointers respectively. offsets,
offset field, etc. are compiler-time errors.
If the TypeSpecification
says READONLY, a relocated pointer cannot be a LeftSide.
The base type must be designated by an identifier (rather
than a TypeSpecification) to avoid syntactic ambiguities. Note
that the form
LONG Typeldentifier
RELATIVE
TypeSpecification
does not have the effect of lengthening the base type and
furthermore is always in error, since LONG cannot
be applied to a relative type. The type designated by the TypeSpecification
can be lengthened (to give a relative long pointer) using
the form
Typeldentifier RELATIVE LONG TypeSpecification
.
Short relative pointers are never made long automatically.
With respect to other operations (assignment, testing
equality, comparison if ordered, etc.), relative pointers behave like ordinary pointers.
In particular, the amount of storage required to store such a pointer is determined
by the TypeSpecification.
Some fine points:
In some applications,
there is no obvious type for the base pointer. i.e., it might not be possible
or desirable to describe
a storage zone using a Mesa type declaration. In
such cases, a declaration such as
BaseType: TYPE = BASE POINTER TO RECORD [UNSPECIFIED] generates a unique
type that will not be confused with other
base types.
The declaration of a
relative pointer does not associate a particular base value with that pointer,
only a basing type.
Thus some care is necessary if multiple base values are in use. Note that the
final type of the relocated pointer is largely independent of the type of the base pointer. Sometimes
this observation can be used to help
distinguish
different classes of base values without producing relOcated pointers with
incompatible types. Consider the following declarations:
boscA:
BaseA: base& BaseB:
OffsetA:
TYPE
= BascA RELATIVE POINTER
TO T:
OffictB: TYPE = BascB RELATIVE POINTER TO T: offserA: OffserA:
offsetB: Offseth .
If BaseA and BascB are distinct types (see the
preceding point). so are OffseiA and Offseth. Expressions such as baseAtoffsetB) and offsctA t offsetB are then errors, but baseA[offsetA] and baseB[offsetBJ have the same type
(71
The base type must have
the attribute BASE. Conversel3, the attribute BASE always takes precedence in
the interpretation of
brackets following a pointer expression. Consider
the following declarations:
p:
POINTER TO ARRAY InciexTge OF ...:
q:
BASE POINTER TO ARRAY IndexType OF .
The
expression p[e] will cause implicit dereferencing
of p and is equivalent to r[e]. On the other hand. q[e] is taken to
specit. relocation of a pointer. even if the type of e is IndexType and not an appropriate relative pointer type. In such cases, the
array must (and always can) be accessed bs adding sufficient
qualification, e.g., vie]: nevertheless, users should
exercise caution in using pointers
to arrays as base pointers.
Mesa currently supplies no special mechanisms for
constructing relative pointers. It is expected that such
values will be created by user-supplied allocators that pass their results
through a LOOPHOLE or
from pointer arithmetic involving LOOPHOLES.
6.3.4. Relative
array descriptors
A RelativeTC constructs
a relative array descriptor type whenever the Typeldentifier evaluates to
a pointer type and the TypeSpecification evaluates to an array
descriptor type. Let a
RelativeTC be
Typeldentifier RELATIVE TypeSpecification,
where
Typeldentifier is of
type
[LONG] BASE POINTER [SubRangeb] TO [READONLY] Tb ,
TypeSpecification is of
type
[LONG]
DESCRIPTOR FOR [READONLY] ARRAY Ti OF Tc
,
and the brackets
indicate optional attributes. Relative array descriptor values must be
relocated before they are indexed. The relocation yields an
expression with type
ARRAY
Ti OF
Tc .
Relative array descriptor types are entirely analogous to
relative pointer types: indeed, values of such types can be viewed
as array descriptors in which the base components are relative pointers. If the
TypeSpecification says
READONLY, the
relocated array (or its elements) cannot be a LeftSide.
In the constructor of a relative array descriptor type,
the TypeSpecification must
evaluate to a
(possibly long) array descriptor type.
In
the notation introduced above, a reference to an element of the described array
has the form
base[offset][i]
where i is
the index of the element.
Currently, relative array descriptors must be constructed using LOOPHOLES.
6.4. Variant
records
Section 3.4 discussed "ordinary" record types.
where every record object of a single type has the same
number and types of components. Such records are not always adequate for
programming applications. For example, in the symbol table for a
compiler, all the records could have certain. components
in common: some standard linkage, a string representing the symbol,
and a category field indicating whether the symbol stands for an
operator, constant, variable, label, etc. Different categories
of symbols would then need further components that were not the same in all the
records.
Variant records are designed for such applications: a
variant record consists of an optional common part followed by a variant part. The common part contains components that are
common to all records of this type. The variant pan contains
the components of each variant of the record.
The specification of a variant record type has
the outward appearance of an ordinary record specification:
REcoRD[field list]. If the record has any common components, these are
specified first; then the variant pan is specified. (The next section shows how this
is done.)
The
variant part really represents a set
of alternative extensions to the common part. The record type
as a whole can be viewed as follows:
Common Pan Variant
Part
Field list for the common pan ---- I---- field list for variant 1
field
list for variant 2
---- field list for variant n
Each individual variant is identified by one (or
more) adjectives. Suppose
defined record type DeRec is declared to have a set of variants named class!. class2, and class3. Then variables could be declared as follows:
someClass: DeRec: -- sometimes
one class, sometimes another
|
firstClass: class! DeRec: secondClass:
class2 DeRec: thirdClass: class3 DeRec:
|
-- strictly a class! DeRec -- strictly a class2 DeRec
-- strictly a class3 DeRec
|
Types like class3
DeRec are bound
variant types. DeRec and class3
DeRec are both type specifications, but the
latter is bound to a particular variant. A variable which is declared as a bound
variant contains a definite variant; these components can be accessed as if
they were common components.
The field list for any variant may, itself, have a
variant part (and a variant in that part may have its own
variant part, etc.). It is possible to have a type like small class3 DeRec (i.e.,
the field list for the class3 variant
has a variant part which, in turn, has a small variant).
The record, someClass,
presents a problem. During the course of execution, someClass might contain
a class], class2, or
class3 variant
record. (Mesa allocates enough storage to hold the largest variant
specified for DeRec type
records.) The problem is to determine which variant applies at a given
time.
To decide which kind of variant a record object contains,
some forin of tag is needed. This tag can be specified as part of the
record, in which case every such record object will contain an ''actual
tag" denoting the variant it represents. Instead of storing a
simple tag. it may be possible to "compute" the
tag value whenever it is needed (possibly by inspecting some values in the
common part). Such computed tags are
much less safe than explicit ones. For instance, you could refer incorrectly
to a "class2" component
of someClass when
it held
a classl variant
record. The result would be undefined.
It is possible to construct an entire variant for the
variant part (sec. 6.4.3) by qualifying a constructor (for
that variant) with the variant's name (an adjective, in other words). Suppose
for example that DeRec has
common components cl and
c2 followed
by a variant part named rp, and that the classl variant has components x and y. Then the record constructor
below constructs an entire classl variant:
DeRec[cl: vall , c2: val2, vp:
class! [x: val3, y: va14]1
Components of an unbound variant can be accessed using the
record's tag value (whether actual or computed). A variation of SELECT beginning
with the keyword WITH
is used for this purpose (sec. 6.4.4).
An example follows (given that DeRec
has a computed tag):
WITH someClass SELECT curren1Tag FROM
class] => Stmt-1; someClass is
a bound classl variant
here class2 => Stmt-2;
someClass is a bound classl variant here class3 => Stmt-3; someClass is a bound class3 variant here
ENDCASE;
6.4.1. Declaring variant records
Variant
records, like ordinary records, are usually declared in two steps:
identifier : TYPE = RecordTC
; --
define record type
IdList : Typeldentifier Initialization ; -- declare the records
Initialization
for variant records (sec. 6.4.3) is similar to that for
ordinary records. The (now complete) definition of RecordTC follows.
It extends the partial definition given in section 3.4.2 and
includes machine-dependent record types:





 MachineDependent RECORD [ Va
riantFieldList
MachineDependent RECORD [ Va
riantFieldList
empty I MACHINE DEPENDENT
CommonPart
identifier : Access VariantPart VariantPart I
NamedFieldList
UnnamedFieldList
empty
I
NamedFieldList ,
SELECT Tag FROM
Va riantList
ENDCASE
empty --
see section 7.4.
PUBLIC
PRIVATE
identifier
: Access TagType COMPUTED TagType
OVERLAID TagType
TagType =
TypeSpecification I*
VariantList = Variant I
VariantList Variant
Variant = IdList
=> [ VariantFieldList ] ,
IdList => NULL
,
The
TypeSpecification in TagType must be equivalent to some
enumeration or enumerated subrange type. If the CommonPart is not
empty, it must be a NamedFieldList. If there is no CommonPart.
the VariantPart itself need not be named.
The following example shows many of the possible
variations resulting from the above syntax definitions. It is unnecessarily
complex for the application, but does show a number of features. It would
be worthwhile to parse the declaration yourself using the definitions given
above. The example might be used to describe the various
"accounts" in a bank; there would supposedly be a table
of such entries, one per account.
Service: TYPE = {savings.
checking, depositBox}: Account: TYPE
= RECORD
number. CARDINAL,
specifics:
SELECT type: Service FROM
savings => [tern: [30..365],
intRate: PerCeta. balance: Money], checking =>
balance:
Money,
monthlyFee: SELECT COMPUTED {free, notfred FROM ',office => [monthlyFee: Money],
free => NULL,
ENDCASE
]•
deposit Box => [fee: Money, dueDate: Date, paid: BOOLEAN],
ENDCASE --
no variant can be attached to the ENDCASE
1:
Each
arm of a VariantPart specifies a single variant, even if a list of adjectives precedes the
"=>". An arm may specify NULL (as in the case of a free checking Account) if that variant needs no components
of its own. Note that all the
arms. including the _final one, must end with a comma.
The adjectives are identifier constants from some
enumeration. Their type can be given explicitly, or implicitly
as an enumeration whose members are the adjectives used in the variant part. In
any case, the enumerated type is the "tag's" type for a
variant part. There are three possible forms for the tag,
and they represent:
an actual tag with
an explicit enumerated type (e.g., type
in Account),
an actual tag implicitly defined (e.g., easyTag in NoCommon below), or a
computed tag (e.g., the monthlyFee for
a checking Account).
If
an actual tag is used, it is allocated in the common part of the record and may
be accessed and used like any other common component, but it may not appear as a LeftSide, since
that would compromise the
type-safeness of such variant records. Not all possible
values from the tag's enumeration type have to be used in a variant
part; some may be omitted.
An asterisk, "*", is used to indicate that the
type of an actual tag is being defined implicitly by the set
of adjectives naming the variants in that tag's variant part. For example,
consider the record declaration below:
NoCommon: TYPE = RECORD
[ no common part
variantPart: SELECT eassTag:
* FROM
i => [compl: INTEGER].
k => [x, comp!: STRING].
ENDCASE]:
The implicit type of easyTag is {ij,k}: note: you can't
declare variables of the same type as easyTag.
Computed lags are
always unnamed. In fact, they arc not really tags at all: when one needs to
know which variant a record with a computed tag contains, some computation must be done.
Exactly how the variant "tag" is computed is strictly up to
the program using it. For instance, to determine whether a checking Account was
free or
not, the program might look at some property of the Account number (such as whether it
was odd or even).
An OVERLAID tag is a special case of a computed tag. The
differences occur in the ways in which fields of the record are
accessed. See
section 6.4.4.
A fine
point
Special care must be
exercised when declaring a MACHINE DEPENDENT variant record. Recall that
MACHINE DEPENDENT
records can contain no "holes" between fields. For variant records,
this leads to the following rules: If the minimum amount of storage required for each variant is a
word or less, each variant must be "padded" to occupy the same number of bits as
the longest. Otherwise, each variant must occupy an integral number of words.
6.4.1. Bound variant types
The declaration of a variant record specifies a type, as
usual. This is the type of the whole record. The variant record
type, itself, defines some other types: one for each variant in the record. Consider
the following example:
StreamType: TYPE = {disk, display, keyboard};
StreamHandle: TYPE = POINTER TO Stream;
Stream: TYPE = RECORD
[Get: PRocEDuRE[StreamHandle] RETURNS[har],
Put: PRocEouRE[StreamHandle, Item],
body: SELECT type:
Stream Type FROM
disk =>
[file: FilePoin ter, position: Position,
SetPosition: PROCEDURE[POINTER TO disk Stream. Position].
buffer. SELECT size: *
FROM
short
=> [b: ShortArray],
long => [b: LongArray],
ENDCASE
display =>
[first:
DisplayControlBlock, last: DisplayControlBlock, height: ScreenPosition, nLines: [0..100]
],
keyboard
=> NULL.
ENDCASE
The record type has three main variants: disk. display, and keyboard. Furthermore, the disk variant has two variants of its
own: short and
long. The
total number of type variations is therefore six. and they
are used in the
following declarations:
r Stream;
rDisk: disk Stream;
rDisplay: display Stream; rKeyb: keyboard Stream; rShort: short disk
Stream; rLong: long disk Stream;
The last five types are called bound variant types. The
rightmost name must be the type identifier for a variant record. The other
names are Adjectives modifying the type identified to their right. Thus, disk modifies
the type Stream and
identifies a new type. Further, short
modifies the type disk Stream and
identifies still another type. Names must occur in order and may not be skipped. (For
instance, short Stream would
be wrong since short does
not identify a Stream variant.)
The formal definition of Typeldentifier can now be
completed (it is only partially defined in Section 2.6.1):
Typeldentifier = I Adjective Typeldentifier
Adjective = identifier
where Adjective is
an adjective of the variant part in the type specified by
Typeldentifier. Note that the recursive use of Typeldentifier in
the first line allows a sequence of adjectives.
6.4.3. Accessing entire variant parts, and
variant constructors
This section considers accesses to entire variant records
(e.g., for initialization), common components of the record
(including an actual tag, if present), and the variant part of the record as a
whole. The next section covers accesses to individual components in
a variant part.
The
common parts of each of the variations of a Stream declared in the previous section can be accessed
by the normal means (qualification and extraction):
rDisk rLong; --
aggregate access
rDisk.Get
rShort.Get; -- selector access
r.body 4-
rDisplay.body: --
selector access
[rDisk. Get, rDisk. body] <-
rLong; -- extractor access
The actual tag, type, in the body variant part may also be accessed by
qualification:
IF rope= StreamType[keyboard] THEN Stmt- I;
It is also possible to construct values of a variant
record type. The syntax of a constructor for a variant part is no
different than a normal constructor except that the identifier preceding the
"[" must be present and must be one of the adjectives used in
defining the variant. For example, some of the following
declarations use constructors to initialize the variables (others use different
forms of initialization):
myDisplay:
display Stream 4- [myGet, myPut, display[dl,d,h,8]]; yourDisplay: display Stream 4- myDisplay;
currentStream: Stream 4- myDisplay;
s: Stream 4- [SysGet, SysPut,
disk [fp, 0, SysSetPos, long[al]]];
The
keyboard variant
of Stream is
a NULL variant: so there
are no 'components for that variant in a keyboard constructor:
rKeyb F Stream [Get:
Kget, Put: Kput. body: keyboard[]1:
A side effect of assigning a bound variant value to a
variable is that the actual tag of the record is also changed. This is the only way to change the variant
contained in a variable (except in the case of a COMPUTED tag) -- it ensures type-safeness. For
example, both the following assignments change the type tag for r
:
rbody 4- keyboard[];
r.body F rKeyb.body; --
always a keyboard variant
If one is assigning a completely bound variant value, by, say (which could
be a constructor, -of course) in an AssignmentExpr (section 2.5.4.),
then the type of the AssignmentExpr is the
type of by,
not the type of the LeftSide, which might not be a
bound variant.
A fine point:
The Mesa compiler does not currently allow an entire
variant part to occur on the right of an assignment as in the fragment above.
Thus, the only way to assign to an entire variant part is via a constructor.
not by copying the variant part of an already initialized record. This restriction
should be lifted in a later release of Mesa.
6.4.4. Accessing components of
variants
When a record is a bound variant, the components of its
variant part may be accessed as if they were common components. For
example, the following assignments are legal:
rDisplay.last 4- rDisplay.first; rDisk.position rShort.position;
If a record is not a bound variant (e.g., r in the previous section),
the program needs a way to decide which variant it is before
accessing variant components. More importantly. however, this must be type-safe.
For this reason, the process of discriminating among possible variants and then
accessing within a variant part is combined in one syntactic form,
called a discrimination, which
is a generalization
of SELECT.
A discrimination closely mirrors the form of SELECT used to declare a variant part. However, the
arms in a discriminating SELECT contain statements or Expressions,
and, within a given arm, the discriminated record value is viewed as a bound variant. Therefore,
within that arm, its variant components may be accessed.
The following syntax equations complete the earlier partial definitions given
in sections 4.3.1 and 4.3.3:
SelectVariant = WITH Openitem
SELECT Tagltem
FROM
ChoiceSeries
ENDCASE FinalStmtChoice
ChoiceSeries = AdjectiveList => Statement
;
ChoiceSeries AdjectiveList => Statement
;
Taglterri =
empty I --
the actual tag is used
Expression --
compute the tag value
FinalStmtChoice = empty
I =>
Statement
|
SelectExp rVa riant
ChoiceList
ChoiceList
Openitem
|
WITH Openitem SELECT
Tagltem
FROM ChoiceList
ENDCASE = > Expression
I
•-•
= AdjectiveList => Expression , I
AdjectiveList => Expression ,
ChoiceList
= AdjectiveList => Expression ,
ChoiceList AdjectiveList => Expression ,
= Expression 1 AlternateName :
Expression -- from sec. 4.4.2
|
The value discriminated is the one given in the WITH clause, which behaves just like an OPEN clause (sec. 4.4.2) to simplify
naming the record value in the arms of the SELECT. The following example discriminates
on r.
WITH
stun: r SELECT FROM
display =>
BEGIN
strm.first
4- stnn.last; stnn.height4-73;
strm.nLines4-4;
END;
disk
=> WITH sirm SELECT FROM
short => b [0]
10:
long => b[0]1-100;
ENDCASE:
ENDCASE => sirm.body
disk [Getip [" Alphal 0, SysSetPos, short[]];
In the first example. suppose r contains a variant record
of display Stream type.
Then the first arm is chosen by this SELECT. Within it, strm (but not r) is considered a record of display Stream type; so
all components of the display variant
may be accessed in the statement chosen by that arm (as they
are in the example).
Suppose
r contains a variant record of
disk Stream type.
Then the actual tag has the value disk,
and the second an is chosen. In this example, only
one of the disk components
is accessed, its variant part. The inner SELECT uses variant record stun. Within the outer arm, Mesa
knows that stnn is
a record of disk
Stream type. Consequently, the tag implicitly used for this SELECT is the tag specified for
that type
(namely, size).
If
the tag value is short, then
the chosen arm accesses component b
in the short
disk Stream variant record; if it is long, then the chosen arm
accesses component b in
the long disk Stream variant
record.
However,
the ENDCASE for
the inner SELECT could
have accessed components that are common to a disk Stream (file, position, SetPosition, variant
part buffer. and
actual tag size; plus
all the original common components: Get, Put, variant part body, and actual tag type).
Suppose, lastly, that r does not contain a variant
record of display Stream or
disk Stream type.
Then the outer ENDCASE
statement is chosen. This statement accesses the common
component body (the
entire variant
part is considered a common component), and gives the record a specific variant
type (short disk Stream) by
wholesale assignment. An ENDCASE may
only access common components; it may
not access components of variants in the given type.
If
the labels on an arm of a descrimination identify more than one variant
stnicture, the record is not considered to he discriminated within that
arm and only the common fields are accessible (cf.
ENDCASE).
Since the outer variant part of Stream was declared using an actual
tag, the tag's value is obtained from the record itself, and no Expression
follows the keyword SELECT (both SELECTS above have this form).
The Expression in the WITH clause (actually in
the OpenItem) must represent either a variant record
or a pointer to a variant record (e.g.. r in
the above). The alternate name is essentially a synonym for that Expression
(e.g., stun in
the above). If it is a pointer, however, the alternate name
designates a record value, not a
pointer value in each arm of the SELECT. In the following example,
the display arm
is correct, and the disk arm
is in error:
rp:
StreamHandle;
proc: PROCEDURE [StreamHandle];
WITH sRec: rp SELECT FROM
display => proc[CsRec]: -- CORRECT
disk =>
proc [sRec]; -- WRONG
ENDCASE;
An open item with no alternative name opens a name scope
so that components can be accessed with implicit qualification
(as in the inner SELECT
of the first example), but then no further levels of WITH...SELECT using
the same record can be done within such a WITH...SELECT. The type of the open item's
Expression indicates the nature of the record's variant part, including
whether the tag is an actual or computed tag, its enumerated type, and
the names of each variant (i.e., the adjectives) in the
variant pan.
If a computed
tag had been used, the program would have to supply an Expression
following SELECT to
determine the variant. This Expression's value would have to be an
adjective in the applicable variant part. For example, assume that tbl[i] in the following has type checking Account (sec. 6.4.1); then
this is a legal (if
not very sophisticated) discrimination for it:
WITH this: tbl[i] SELECT (IF (this.number MOD 2) = 0 THEN free ELSE notfree) FROM
free => NULL;
notfree => AddToBill[this.monthlyFee];
ENDCASE:
If
a given arm of a discrimination is labelled by indentifier constants
corresponding to more than one variant of the record, only the common fields
of the record are accessible within that arm.
The record value in a WITH clause must not represent a completely bound
variant (which is really not a variant at all). For example. a valid discrimination for a disk Stream record, aDiskStream, follows:
WITH aDiskStream SELECT FROM
short
=> b[0]<-10:
long => b[0]4-100;
ENDCASE:
It would be illegal to rewrite this
as follows:
WITH alt: aDiskStream SELECT FROM -- WRONG! disk => WITH alt SELECT FROM
short
=> b[0]<-10:
long => b [0] *-100:
ENDCASE;
ENDCASE;
An OVERLAID record is a special case of
a computed variant record in that there is no explicit tag field
in the record. The fields of' the individual variants may be accessed using a
"computed" WITH
construct in the same manner as a COMPUTED record.
In addition. any field name of a variant that is unambiguous (i.e.
it appears in only one variant) can be referenced without descrimination. In essence,
the programmer is telling the compiler When I use a fieldname, you
can trust me that the record has the proper variant." Consider the following example:
TrustMe: TYPE = RECORD[
SELECT OVERLAID * FROM
one => CHARACTER, i: CARDINAL, next:
POINTER TO TrusiAle].
two => [b:
BOOLEAN, next:
POINTER TO TrustMe],
three => [S: STRING],
ENDCASE]:
I: Trust]Ile;
t.c --
legal
Lb --
legal
Lnext --
illegal, both variants one and
two contain
such a field.
A fine point
In the declaration of TrustMe above, the two next fields were of the same type, but
occuppied different positions within the record. Even if they did occupy the
same position, one could still not refer to Lnext. The ambiauity is one of variant, not of value.
CHAPTER 7.
MODULES, PROGRAMS,
AND CONFIGURATIONS
Large programs in Mesa are constructed by linking or
binding together individual modules..
A module is the basic unit of compilation and also
the smallest, self-contained, executable program unit. Most of this
chapter deals with how separate modules are put together to build large
systems; i.e., it deals with programming in the large as opposed to programming in the small (which
is what this manual has discussed so far).
There are two fairly distinct kinds of modules. Definitions modules serve
primarily as "blueprints" or specifications for how
the parts of a system will fit together. During compilation they provide a common
(and therefore consistent) set of definitions which can be referenced by other
modules being compiled. The second kind of modules, called programs, contain actual
data and executable code. Program modules can be loaded and
interconnected to form complete systems.
Mesa compiles a program module's source code (which is
just a text file) into an object
module. An object module is a binary file containing object
code, symbol table information, and data structures to
be used in connecting (also called binding)
this module together with others. Compiling a definitions
module produces symbol table information only, which may then be used in
compiling other modules (either definitions or program modules).
7.1. Interfaces
An interface is
a connector between programs; it allows code in one module to access parts of
other modules—specifically, procedures, signals (chapter 8) and
variables. Interfaces are defined by definitions modules
(section 7.3). They contain declarations for public items and allows the
compiler to check for type matching across inter-module references.
The interface, considered as a record, also proves a convenient
data structure for efficient binding together of programs.
The procedures that implement a given abstraction are
often collected in a single interface. For example, an
interface for an allocator might consist of the names and types of the
procedures for allocating and freeing blocks of storage, and
pointers to shared blocks of storage. The data types required
by these procedure types (for parameters and return values) are usually defined
in the same definitions module. Such non-interface types are available for reference when compiling
other modules, but are not considered part of the interface
specified by that definitions module.
At compile time, a program module containing calls on
procedures defined by some interface must import the definitions module that specifies that interface.
This enables the compiler to check the agreement of types of
parameters and return values on calls from that module with their counterparts
in the definitions module (i.e., as defined in the interface). Importing the interface at compile time
does not, however, link the procedure references in the program module to
actual
procedures in some other module(s).
That actual binding
occurs later when the compiled module is linked
with other compiled program modules
to make a system (sec. 7.7).
.1he actual implementation of an interface is
usually provided by a single program module. although it
may be realized by
a group of modules. each supplying a part. In any case, if a program module implements
(all or part of) the interface specified by a definitions module. it is said to
export that
interface. The procedures and variables in that program
corresponding to the ones in the exported interface must be
type-compatible with them (sec.
5.2). The compiler checks that this is so.
After compilation, a program
module contains a set of virtual
interface records, one for each imported interface,
and a set of export records, one
for each exported interface (a single program module can
implement more than one interface). Binding a group of modules together into a system
then involves associating virtual interface records with exported
interfaces for all the modules in the group.
The
following definitions module, IODefs,
provides a minimal (and unrealistic) interface to a computer
terminal:
IODefs: DEFINITIONS =
BEGIN
-- Interface definitions
ReadChar: PROCEDURE RETURNS [CHARACTER];
ReadLine: PROCEDURE [input: STRING]; --
reads from terminal into input
WriteChar:
PROCEDURE [ouput: CHARACTER]; WriteLine:
PROCEDURE [output: STRING]:
10Pkg: PROGRAM;
-- Non-interface definitions
CR: CHARACTER = 015C; -- an ASCII Carriage-Return character END. -- IODefs
The interface record for IODefs is imported by the
following Copier program
module. The program reads lines from the terminal and retypes them.
When the user types a line beginning with a period, it
writes a parting message and stops:
DIRECTORY
IODefs: FROM "IODefs":
Copier. PROGRAM IMPORTS 10Defs =
BEGIN OPEN 10Defs; -- allows
simple references to items from 10Defs
input: STRING 4- [256]: -- 256-character string to hold
input lines typed by user
-- the mainline part of the program starts here:
DO --
infinite loop: only left by EXIT
ReadLine[inpul]: --
read a line into input
IF input [0] = THEN EXIT: --
quit if first character is a period
WriteLine[input]; --
otherwise copy it back to the user
ENDLOOP;
WriteLine["End of
example."]; --
final output
WriteChar [CR]; --
leave terminal on a new line
END. --
Copier
The skeleton of a module that implements the IODefs interface follows. It EXPORTS IODefs and IMPORTS nothing:
DIRECTORY
IODefs: FROM "IODefs":
IOPkg: PROGRAM EXPORTS IODefs =
-- this module contains the actual procedures for the
interface specified by 10Defs.
BEGIN
terminaNtate: {of on, hung} <-
off --
initial state of the terminal
ReadChar: PUBLIC PROCEDURE RETURNS [CHARACTER] = BEGIN . END; ReadLine: PUBLIC PROCEDURE [input: STRING]
= BEGIN ... END;
WriteChar: PUBLIC PROCEDURE [ouput: CHARACTER] = BEGIN . END; WriteLine:
PUBLIC PROCEDURE [output: STRING] = BEGIN . END; END. -- 10Pkg
The
next step towards running the above modules as a system requires binding them together. Binding
is the process of matching up virtual import records with real export records.
A separate language, C/Mesa, is used to describe binding.
This language has a syntax similar to Mesa's, but is much smaller.
C/Mesa "programs" are compiled ("processed" might be more
accurate) by a program called the Binder. The C/Mesa source code is called a Configuration Description (CD), and compiling one results in a Binary Configuration Description (BCD)
file. An object file produced by the Mesa compiler is actually a
very simple BCD containing just one module's object code and
binding information.
BCD files can be loaded and run. (Actually, it is the
individual modules in the BCD that are loaded). This loading also
alters all the BCD's virtual import records to hold real procedure descriptors
(sec. 5.2), signals, and pointers to program frames. Then the modules
comprising the BCD can all be started (details in sec. 7.8).
The following CD describes a system of three modules: Copier, 10Pkg, and Driver.
AfakeCopierSystern: CONFIGURATION
CONTROL Driver =
BEGIN Copier, 10Pkg; Driver; END.
This configuration specifies how the Copier, 10Pkg, and Driver object modules are to be
bound together. Simply listing their names is all that is
usually required in a CD. Now the Mesa loader could load the
complete program using the BCD file for MakeCopierSystern. Driver is named as the CONTROL module
for the BCD, so starting the loaded BCD would actually result in starting Driver, which follows:
DIRECTORY
IODefs: FROM "iodefs''. Copier FROM "copier";
Driver PROGRAM IMPORTS Copier, IODefs =
BEGIN
START 10Defs.10Pkg: --
so its variables (e.g., terminalState) are initialized
START Copier -- to
initialize its variables and run its mainline code
END.
This example is simple, but MakeCopierSystern and
Driver would
still be simple even if the system had 50 modules instead of
just two. For this example, they seem like excess baggage, but for a larger
system, they are invaluable because:
(a) they
describe exactly how the various modules are bound together and initialized:
(b) C/Mesa
allows Mesa's compile-time checks on types to extend to binding time: (c)
loading and linking with this scheme can be very efficient.
We
can now give the details of Mesa DEFINITIONS and PROGRAM modules.
Section 7.7 discusses C/Mesa and how it is used.
7.2. The fundamentals of Mesa modules
The
complete syntax for a module is the following:
 CompilationUnit
CompilationUnit
Access Directory ExportsList FileName GlobalAccess
ImportsList
Includeltem
IncludeList ModuleBody
ModuleHead
Interfaceltem InterfaceList LocksClause
ModuleName
ProgramTC
ShareList
= Directory --
optional
ModuleName : ModuleHead = GlobalAccess
ModuleBody
empty I PUBLIC I PRIVATE
empty I DIRECTORY IncludeList
empty I EXPORTS IdList -- sec. 7.4.6
stringLiteral --
sec. 6.1.1
Access --
sec. 7.4.3
empty I IMPORTS InterfaceList
-- sec.
7.4.6
= identifier
: FROM FileName I
identifier : FROM FileName
USING [ IdList ]
=
Includeltem I
Includeltem , IncludeList
= Block . --
sec. 4.4
-- note the terminating period
= DEFINITIONS LocksClause ImportsList ShareList ProgramTC ImportsList ExportsList ShareList
identifier I identifier : identifier Interfaceltem I InterfaceList , Interfaceltem
= empty I --
sec. 10.4.1
LOCKS Expression I
LOCKS
Expression USING identifier : TypeSpecification
= identifier
= PROGRAM ParameterList ReturnsClause
MONITOR
ParameterList
ReturnsClause LocksClause
= empty I SHARES IdList -- sec. 7.4.6
A
DEFINITIONS module
can serve a twofold purpose: it can define an interface, and may contain declarations
of constants and types. Definitions modules are further discussed in section
7.3.
The text of a program module X implicitly defines
a frame type, FRAME[X].
Values of this type are created dynamically by loading X and can only be
accessed indirectly; i.e., a program may have variables of type POINTER TO FRAME[X],
but never of type FRAME[X]. A module's frame contains storage
for its variables, along with some system overhead.
We
will first deal with the initial syntactic unit which is common to all modules
(the Directory clause),
then with DEFINITIONS modules
as a whole. After these sections there is a complete example


 a client
program that uses it, and
a client
program that uses it, and
a configuration that hinds the programs together into a
system.
7.2.1. Including modules: the DIRECTORY clause
The
source code for a given module may tell the compiler to include previously compiled modules
for one or more of the following reasons:
It might need to use some of the symbols defined by those
modules. It may need to import the interfaces defined by those
modules.
It
might refer to instances of such modules after they are loaded in order to START them,
to make new instances of them, or to access their data.
Suppose module A
is included in module B. This means that when compiling B, the compiler must have
access to A's object file (i.e., A must
have been compiled previously) in order to access its symbol table to obtain
information needed by B. Warning:
including a module is not simply
an insertion of text from one module
into another—it is important to read these sections carefully to use this
capability correctly.
The following is a simple, but complete DEFINITIONS module:
SimpleDefs: DEFINITIONS =
BEGIN
limit: INTEGER = 86:
Range: TYPE = [—
Pair: TYPE = RECORD[first. second: Range]; PairPtr. TYPE = POINTER TO Pair
END.
Suppose that the above source code is contained in a file
named "SimpleDefs.mesa". After compilation, anyone who has
a copy of the object file for SimpleDefs
(which will be named "SimpleDefs.bcd"
by the compiler), may then include it in other modules. The ".bcd"
portion of the file name stands for Binary Configuration Description
(sec. 7.6.3) of which a compiled module is the simplest
example. The ".bcd" part of the name need not be specified in the
directory section (see below).
A module that includes
other modules begins with a Directory. which performs two functions:
(1) It
associates a Mesa identifier with the name of an object module (which does not necessarily
look like a Mesa identifier).
(2) It checks that the
given identifier matches the ModuleName in the module whose object file
is named.
Here is an example of a DIRECTORY: DIRECTORY
SimpleDefs:
FROM "simpledefs", StringDefs: FROM "stringdefs":
7.2.1.1. Enumerating items from an
included module: the USING clause
A module may list the symbols it expects to access from an
included module in the USING
clause of an Includeltem. If a USING clause is present. it must
list all of the
symbols to be included: the compiler will not allow access to any symbol not in
the list. Warnings will he issued for symbols appearing in the
list which are not referenced in the module. In this way, the USING clause
accurately documents which symbols are defined in each
included module.
Here is an example of a DIRECTORY with
a USING
clause:
DIRECTORY
SimpleDefs:
FROM "simpledefs" USING [Range, Pair], StringDefs: FROM
"stringdefs":
A module with this DIRECTORY statement would be allowed
to use the symbols Range and
Pair defined
in SimpleDefs, but
would not be allowed to use any other symbols defined in SimpleDefs. Access to symbols
defined in StringDefs is
not restricted.
The
USING clause
only allows and restricts access to symbols. Actual references to the symbols
must be made in one of the ways described below.
7.2.2. Accessing items from an
included module
This section describes the ways of accessing symbols
defined in an included module:
An
identifier, p, defined
in a definitions module, Defs, can
be named in an including module, User,
in one of two ways.
Explicit qualification: p can
be named as Defs.p in
User.
OPEN clauses: In the scope of an OPEN clause of the form "OPEN Defs", the simple name p suffices.
The remainder of this section gives more detail on these
methods.
7.2.2.1. Qualification
In the following example, qualification is the
only access method used:
DIRECTORY
SimpleDefs: FROM "SimpleDefs":
TableDefs: DEFINITIONS
= BEGIN
limit: INTEGER = 256:
-- this has no connection with SimpleDefs.limit
Index: TYPE = [0..limit):
SiringTable: TYPE = ARRAY Index OF
STRING:
PairTable: TYPE = ARRAY Index
OF SimpleDefs.Pair,
END.
SimpleDefs.Pair means
"the item named Pair in
SimpleDefs." As
a rule, qualification provides more readable code than do the
other methods for specifying the use of predefined symbols. However, it can be
inconvenient if there are many such occurrences because two identifiers have to
be written instead of one.
No names are included
automatically when only explicit qualification is used. For example, if
TableDefs had
not declared limit. Mesa
would not ha% e used the' one in SimpleDefs.
An error would then result when TableDel's was compiled
(because Jinni is
needed in the declaration of the type Index).
Any module that includes TableDefs may use only the symbols
defined by it, but to use Pan: that
module would have to include SimpleDefs (as in the next
section's example). Declared symbols in the included
module do not include record component names: they are part of a records type specification
and can be used wherever
the record type is known.
A
qualified name may denote a type defined in an included module (e.g.. the type SimpleDefs.Pair in the example in
the previous section). Thus the syntax for Typeldentifier includes the
case
Typeldentifier :: = I identifier .
identifier
7.2.2.2. OPEN clauses
The
following program, TableUser, includes
both SimpleDefs and
TableDefs. It
accesses names from SimpleDefs by
qualification, but uses an OPEN clause to access items from TableDefs:
DIRECTORY
SimpleDefs:
FROM ''simpledefs" USING [Pair], TableDefs: FROM
"tabledefs":
Tablellser. PROGRAM =
BEGIN OPEN TableDefs: -- (Notice
the OPEN-clause.)
\Index: INTEGER 4- limit: -- this
is TableDefs.limil because
of the OPEN
IString: SiringTable;
vPair.
PairTable:
StoreString: PUBLIC
PROCEDURE[s: STRING, v: Index] =
BEGIN
vString[v] s:
vPair[vIndexi-v] (- NIL;
END:
StorePair: PUBLIC
PROCEDURE[t: SimpleDefs.Pair] RETURNS[ok:
BOOLEAN] = BEGIN
ok I.Index<= limit:
IF ok THEN vPair[vIndex] t:
END:
END.
In the scope of the OPEN clause, the names limit, String Table. PairTable. and
Index are
those in TableDefs. The
scope of these OPEN clauses
follows the same rules as the OPEN clauses for records described in section 4.4.2.
In fact, a single OPEN
clause can contain Openitems that open either modules
or records.
TableDefs could
have been in an OPEN clause
anywhere that one is permitted. This feature can be used to help the readers of
a program. For example, if the names from TableDefs were only needed in the procedure StoreSiring, we could put an "OPEN TableDefs" on its BEGIN rather
than on the BEGIN for
the whole module. This would localize the region
of the program where a reader would have to consider whether an identifier is from an included module
or not.
Fine
point:
Note that qualification is still
required to reference SimpleDefs.Pair even though Pair appears in the USING clause.
7.2.3. Scopes for identifiers in a
module
'Me
use of identifiers appearing in modules falls into two broad categories, defining occurrences (e.g..
to the left of the ":" in a declaration), and name references (such as the
appearance of a name in an
Expression). Scope rules determine
which defining occurrence goes with a given reference. In
Mesa,
these rules are lexical.
i.e., they depend only on the textual structure of the module at
compile-time.
A name scope
is itNays a contiguous region of a module
(e.g.. ever“hing between a BEGIN
... END pair. or between a [ ] pair) and may contain other scopes nested
within it. The first scope rule is the following:
Within
a single scope (excluding scopes nested within it), there
can be at most one defining occurrence of a given
identifier.
An
important corollary of this rule is that a given identifier is either undefined
in a scope or it has exactly one meaning.
A
qualified name
reference demands an exact context for its qualified identifier. For example.
SimpleDefs.Pair --
(sec. 7.2.2.1) qualification by module name; context is SimpleDefs
rDisk.Get --
(sec. 6.3.3) record qualification; context is disk Stream, the
type of rDisk
winner.party --
(sec. 3.4) pointer qualification: context is Person, the reference type of
winner
The rule of scope is simple for a qualified reference:
The
qualified identifier is associated with its symbol definition in the specified
scope (if there is no such defined name, the qualified identifier
is undefined and there is an error).
An
unqualified name
reference occurs within a sequence of nested scopes (as indicated below). The rule
of scope is
lise the innermost
scope that defines the referenced identifier (if none of
the scopes do so, the identifier is undefined and there is an error).
New name scopes are created by the following:
OPEN clauses
Blocks
with declarations
enumerated types and their subrange types
record
types that use named field lists
procedure types that use named parameters or results actual
procedures
exit
regions for loops and compound statements
the heads and arms of discriminating SELECT statements
OPEN clauses may introduce
multiple name scopes, which are nested (inner-to-outer) in order from right
to left. Consider the
following revision of the earlier TableUser
module:
DIRECTORY
SiMp/CDefS: FROM "simpledefs",
TableDefs: FROM "tabledefs";
TableUser: PROGRAM =
BEGIN OPEN .S'impleDefs.
TableDefs:
StorePair: PUBLIC
PROCEDURE[/: Paid RETURNS[ok:
BOOLEAN] =
• • •
Notice that we no longer need qualification for the
parameter type of procedure StorePair.
When the compiler encounters identifier Pair, it finds the needed symbol
definition in the symbol table for included module SimpleDefs. The path by which
it found this is the following: it looked for such a definition
in the current module. but failed there: it then tried the next outer scope,
which according to the OPEN was TableDefs:
not finding Pair
there either, it went on to the next (and outermost) scope
given by the OPEN, namely. SimpleDefs, at which point a defining occurrence was found.
Localizing the scope of identifiers from included modules
is so important that we recommend the following naming guidelines:
(1) Place
a USING clause
on items in the DIRECTORY.
This collects in one place a list of all symbols
referenced from each included module. The list is always accurate because the compiler
checks it on each compilation.
(2)
Use explicit qualification as the normal way of
naming an external item.
(3) Use an OPEN clause on the smallest possible scope when
explicit qualification becomes too verbose. It is unusual for
items from an included module to be accessed with high frequency
everywhere in a module: most often, there are clusters of references to them.
An OPEN clause
takes advantage of this clustering and alerts a reader to it.
7.2.4. Implications of recompiling included
modules
Consider a set of modules Adefs, Userl, and User2 where Adefs is included in Userl and User2. (For simplicity, assume Userl and User2 include only module Adefs.) Suppose Adefs and User! have already been compiled,
but before User2 is
compiled, Adefs is recompiled for
some reason. Then User! must also be recompiled.
In general, recompiling Adefs will invalidate the current
version of Userl. This
is obvious when Adefs undergoes
significant change between compilations, but it may also be true
when seemingly innocuous changes are made. In fact, if User! uses record or enumeration
types defined by Adefs, the
current version of Userl is
invalidated when Adefs is
recompiled, even if no changes
are made to its source code!
For example. suppose Adefs defines RECORD type Account which is used by User! as the type of rl and
by User2 for
r2. Normally, one would expect these records to have the same type. If events occur
as follows, however, they will not:
Adefs is
compiled.
Userl is compiled including (old) Adefs. Adefs
is recompiled.
User2 is
compiled including (new) Adefs.
The record types for rl and r2 will differ because of the
way Mesa guarantees uniqueness for record types. The compiler
associates a "time stamp" (e.g., time of definition) with each record
type. Old Adefs defined
Account at
one time and new Adefs defined
it a later time; this makes them different (non-equivalent)
record types which only "look" the same.
Consider the case where Defsl is included in Defs2. and Defs2
is included in User!.
(For simplicity, assume that Defs2 includes only Defsl and User! only Defs2.) Suppose that Defsl is recompiled and then
Defs2 is
recompiled. Then Userl should also
be recompiled. The reason for this is the uniqueness
of record types defined in Defs2 and
used by User!.
The (re)compilations of Defsl. Defs2, and User!
must occur in a specific order: first Defsl, then Defs2. and finally User!. Suppose. however. that User! included Defs2 plus another module Defs3, and suppose Defs3 included Defsl. The following diagram
illustrates these dependencies. Modules which are included are above modules
which include them. The rule for avoiding errors due to incorrect
compilation order is the following: a module may not be (re)compiled until all
the modules above it have been.
Defsl

 Defs2 De
s3
Defs2 De
s3
 Userl
Userl
Thus, Userl should
be recompiled after Defs2 and
Defs3 have
both been
(re)compiled. The order in which Defs2 and Defs3
are compiled is unimportant, however. Moral: There is an important partial order
defined on modules by their inclusion relations.
7.3. DEFINITIONS modules
Generally, a DEFINITIONS module contains a set of
related definitions. There are compile-time constants, types, and procedure and
signal definitions. There are also declarations of so called interface variables (section
7.3.1). These definitions are used by the prozram(s) that implement those procedures,
and they are used by programs that only wish to call on those procedures.
Separating definitions from implementations allows programs that
call those procedures to be independent of changes in implementation.
The definitions in a DEFINITIONS module fall into two
classes:
Interface elements: definitions
for interfaces (procedures, signals, programs and interface variables),
and
Non-interface elements: compile-time
constants (this includes TYPE definitions)
There are no special rules about which valid compile-time
constants may be used other than the issues surrounding
compilation order (sec. 7.2.4). External
interface definitions, however, are
different. Normally, a declaration such as
SampleProc: PROCEDURE [I:
INTEGER]:
declares a
procedure variable. In a DEFINITIONS module, however. its effect is to define the type and name
of a procedure component of the interface specified by that definitions module.
Section 7.6 contains an example of a DEFINITIONS module that defines
procedure interfaces.
In the same manner, signals, errors, and programs can be
declared in a DEFINITIONS
module as elements of its interface
type. A signal or error declaration is treated just like a procedure as an interface
element. A program definition as an interface element is discussed in section
7.4.3.
7.3.1. Interfirce variables
Just as procedures are often declared in one program
module and called from another, there are often applications that
require sharing of non-procedural variables, such as common data structures.
One means to allow common variables is via interface variables-. These are variables that
are defined in a DEFINITIONS module. but must be exported by some
implementing program before they actually exist. Variable declarations in
interfaces are like those in programs. with one additional option.
Declaration =
IdList : Access ReadOnlyOption EntryOption
TypeSpecification Initialization ;
ReadOnlyOption = empty I READONLY
The READONLY option can be attached to a variable only in an
interface. If this option is specified, importers can read the
variable but not update it; otherwise. importers are able to read and update
the variable freely. Note that a READONLY variable is not necessariln, constant: it can be changed from
within the program module exporting
the variable. Consider the following example:
Defs: DEFINITIONS = BEGIN
|
varl:
var2: READONLY T;
END.
|
|
|
|
Imp!: PROGRAM
|
EXPORTS
|
Defs
|
=
|
|
BEGIN
varl: PUBLIC
var2: PUBLIC
|
T;
T;
|
|
|
|
varl 4- el;
|
var2 F
|
e2;
|
|
END.
|
|
|
|
|
User: PROGRAM
|
IMPORTS
|
Defs
|
=
|
BEGIN
Defs. varl e3;
IF Defs.var2 = e9 THEN ...
END.
In this example, the
exporter (Impl) provides
storage for the variables varl and
var2. Within
Impl, both
are ordinary variables, e.g.. var2 can
be updated. By importing Defs, the
client (User) gains
access to the storage for varl and var2 but cannot update var2. Although Defs.varl and Defs.var2 are referenced
indirectly, through pointers in User
initialized by the binder or loader, those pointers are
invisible to the
importer and are always automatically dereferenced.
An
interface variable must be declared with the attribute PUBLIC in
the exporter. It must not be declared with fixed
("=") initialization. Assignment (".-") initialization is
permissible: note, however. that such initialization is not
performed until the exporting module is started, and reference to an
interface variable does not cause a start trap in the exporter (see section 7.8.3).
A
line point: If an interface component has a PROCEDURE. SIGNAL. ERROR or
PROGRAM tspe. ann importer expects that component to contain an
actual value (e.g.. a procedure descriptor). not a pointer to such a value. Thus an interface xariable cannot hale one of these types. For
example. if the declaration
Proc: PROCEDURE [ ...]:
appears
in a DEFINITIONS 'nodule Mfr. the declaration
Proc: PUBLIC PROCEDURE
[...] = BEGIN ... END:
is
salid in an exporter of Defs the declaration
Proc: PUBLIC PROCEDURE
[...] F .S'omeProcedure:
is not. (In
the latter case_ a sariable containing a pointer
to Proc could be exponed.)
In addition to providing common access to data structures,
interface variables make default fields (section 7.3.2) and inline procedures
(section 7.3.3) more useful in DEFINITIONS modules; that is, interface variables can be used
within these definitions to access nonconstant information in the exporter.
Interface variables used for this purpose must be PUBLIC in
the exporter but can.
be declared with the attribute PRIVATE in
the DEFINITIONS module.
This convention is strongly recommended to prevent
unintended direct sharing of the variables by clients of the interface. Note that
code within an interface cannot update a READONLY component of that
interface.
We will see in section 7.4.2 another means of
accessing the variables of another program module, that
of an implicit POINTER
TO FRAME[...]. whose value is initialized by the loader. This
offers an alternative to interface variables, but leads to
compilation dependencies such as those described in section 7.2.4. In choosing between the two methods, note the following:
Each imported interface variable introduces a separate
pointer in the link area of the importer (see Section 7.7,
page 125). On the other hand, each access to such a variable generally
requires less code and is faster than an access to a field of an imported
frame.
The use of interface variables introduces less severe compilation dependencies;
recompilation of the exporter does not require
recompilation of all importers.
Compromise positions are also possible. Information to be
shared can be grouped into a smaller number of variables with record or array
types. and those variables can be exported. This reduces the
number of pointers but increases the amount of (potentially changing) structure
in the interface.
7.3.2. Default fields in interfaces
One valuable use of interface variables is in default
values for procedure argument records (section 5.1). Default
arguments can contain references to procedures ONLINE or otherwise), signals and interface
variables that are components of the same interface. These references are bound
to values in the same instance of the imported interface as the one
supplying the procedure definition itself. References to
non-constant components of other interfaces require that those interfaces be
imported by the DEFINITIONS module and all its users (see section 7.4.4).
For example, an interface could contain:
globalQ: PRIVATE
Queue: -- an interface variable
Add: PROCEDURE [i: Item, q: Queue 4- globalQ]:
This
declaration allow users to Add items
to globalQ, but
not to access the variable directly. Thus the statement
is equivalent to
Defsl.Add[myltem, Defsl.globalQ];
A fine
point:
If a program imports two instances of DOI, saN D1 and D2. the defaulted %Are for q will be from the same instance as the
called procedure. In
other words.
DLAdd[mylwrii] is
equkalent to Dl..-ili[mv Item
Dl.globalQ). •
D2.Add[m)lrem] is equivalent to D2.Add[mylian
In a program module, default arguments of exported
procedures (and signals. etc.) require special attention. Because of the
assignment rule. the DefaultOptions
specified in the exporter and in the interface
are not required
to agree. If the implementer and the clients are to behave identically with respect
to defaults. the same DefaultSpecification must appear twice.
For example, if the interface has the declaration
Proc: PROCEDURE [x:
T 4- el];
and
the exporter has the declaration
Proc: PUBLIC PROCEDURE
[X.' T e2]
= BEGIN ...
END;
then within the exporter, Proc[] means Proc[e2]; within an importer of the
interface, Proc[] means
Proc[0]. The
langauge requires only that the types of el and e2
be compatible with T; if they should also provide the
same value, the programmer must ensure this.
7.3.3. Hine procedures in interfaces
An
INLINE procedure
can be declared within a DEFINITIONS module. Any caller of that procedure must
import an instance of the corresponding interface.
Within a DEFINITIONS module, the body of an INLINE procedure
can contain references to procedures (INLINE or otherwise), signals and
interface variables that are components of the same interface. These
references are bound to values in the same instance of the imported interface
as the one supplying the inline procedure itself. References to
non-constant components of other interfaces require that those interfaces be
imported by the DEFINITIONS
module and all its users (see section 7.4.4).
Interface components with the attribute PRIVATE are
visible to the bodies of inline procedures declared within the
same DEFINITIONS module.
An inline procedure referencing such components can be imported
into a PROGRAM module
in which those components are not visible. Interface components used only as
free variables or default arguments of imported procedures should not be
mentioned in the corresponding USING clauses. For example, suppose that an interface contains
the following declarations:
DoinainFault: SIGNAL;
Proc: PROCEDURE
[CARDINAL] RETURNS [T]:
N: CARDINAL = 100:
Table: PRIVATE ARRAY [0 N)
OF
POINTER TO T:
IProc: PROCEDURE [i: CARDINAL] RETURNS [T] = INLINE BEGIN
IF i —IN
[0 A) THEN ERROR DomainFault:
RETURN
[IF Table[i] = NIL THEN Proc[i]
ELSE
Table[i]t] END:
Note that the body of an INLINE procedure (IProc) can contain references to
constants (N), interface procedures (Proc), signals (Domain•ault) and interface variables (Table) in the same interface. If Defsl is an instance of this
interface, Defs1.1Proc references
Defsl.Table, calls
Defsl.Proc, etc.
An importer cannot reference Table directly because of the PRIVATE attribute
but can reference it indirectly through IProc.
It
is not legal for a PROGRAM
module Progl to
call an inline procedure defined in some other PROGRAM module Prog2, even if Progl imports a POINTER TO FRAME[Prog2].
7.3.4 Usage hints for INLINE procedures in interfaces *
Expansion of inline procedures can cause internal data
structures of the compiler to grow rapidly: indiscriminate use
of the INLINE attribute
can substantially degrade compiler performance or cause tables
to overflow. The current compiler has been organized so that inline expansion
is particularly efficient, and incurs little added overhead, in
the following circumstances:
The INLINE procedure, with an arbitrarily complex body, is
defined within a PROGRAM
module and called exactly once in that same module. (Thus introducing named
procedures for clarifying and structuring a program can be cheap
when such procedures are called only once.)
The INLINE procedure, defined either in a DEFINITIONS module
or a PROGRAM module
and called an arbitrary number of times, is very simple, with
no local variables, no named output
parameters, and no side effects.
The debugger cannot set breakpoints within. or display the
expanded source text of, an INLINE procedure (although it can display the local
variables resulting from the expansion). Debugging can be
easier if the INLINE attribute
is used only as needed and is specified after initial testing has been successfully
completed.
7.4. PROGRAM modules: IMPORTS and EXPORTS
A PROGRAM module may contain
definitions of constants and types (just like a DEFINITIONS module),
declarations of variables.
actual procedures and signals (chapter 8), and
executable statements of its own (i.e., not part of
procedure bodies within it).
At run time, a loaded module (also called an instance of the module—sec. 7.6.3)
has a frame which provides storage for its declared variables and
for connections to other modules' procedures and signals.
These connections are called interface records. and
there is one for each interface imported by the module. The Mesa
binding process fills in these interface records with procedure descriptors.
signal codes. and
pointers to program frames and exported variables in other modules.
7.4.1. IMPORTS. interface
types, and interface records
The IMPORTS list for a program
declares which interface records the program needs and associates them
with DEFINITIONS modules
(called interface opes). Interface
records and inter:face types are different!
A program may only access non-interface elements using an
interface type. but can access all elements (both interface
and non-interface) when using an interface record.
The names of interface records are declared in a PROGRAM module's
IMPORTS list.
The identifier preceding a ":" in the list names an
interface record, while the name following that same ":" must name an
interface type. In the following example. names ending with Rec specify interface records, and
names ending in Defs specify
interface types:
DIRECTORY Defsl:
FROM
"defsl", Defs2: FROM "defs2": Prog: PROGRAM IMPORTS IRec: Defsl. I2Rec: Defs2 =
BEGIN . . . END.
Within the body of Prog, references like Defs1.x are only valid if x is a non-interface element of
Defsl. However,
IRec.x can
refer to any element x of Defsl, whether
interface or non-interface. This distinction is
necessary because a call on a procedure, proc, defined in Defsl. must refer to the actual descriptor
in the interface record IRec at
run time, not just to its compile-time definition.
Omitting the name of an interface record in an IMPORTS list
and giving only the name of an interface type means that
the record's name should be the same as the type's. For example, writing
Prog: PROGRAM IMPORTS IRec: Defsl. Defs2 = . . is the same as writing
Prog: PROGRAM IMPORTS IRec: Defsl, Defs2: De_fs2 = .
Then. within the body of Prog. Defs2 refers to an interface record. In fact it is
impossible thereafter to refer to the interface type Defs2, although one can still refer
to the interface type Defsl because
its name has not been reused.
Sometimes one needs to have access to more than
one instance of an interface record at run time. For example. the
Mesa compiler needs to access one instance of a symbol table package for the program
that it is compiling, and at least one for the symbol tables for modules
included by that program. This can be done by defining a number
of interface records for a single interface type, as in
the following:
DIRECTORY SyinDefs: FROM "SymDefs":
PartOICompiIer: PROGRAM IMPORTS tnainSyrn: SymDefs, auxSynt:
.S.yrnDefs =
BEGIN ... END.
Within the body of Part0fCompiler, one would access an interface element of SyrnDefs named LookUp for the main symbol table as
mainSynt.LookUp, and
for the auxiliary symbol table as auxSym.LookUp.
7.4.2. Importing program ?nodules
Any module can include a program module X by naming
X in
its directory. One can use X to declare program variables of type POINTER TO FRAME[X].
FRAME1,11 is
not a valid type because frames cannot be embedded in other structures.
One may obtain a value for POINTER TO FRAME[X] is from a system procedure as described in the Mesa
.S'ystem Documentation, or by IMPORTing.
A module can import a program X by naming it in
its IMPORTS
list. For example, DIRECTORY A'Progl: FROM "XProal",
XProg2: FROM "XProgr:
Prog: PROGRAM IMPORTS framel: XProgl. XProg2 =
BEGIN . .
END.
This has an effect similar to declaring
framel: POINTER TO FRAN4E[XProgn = . XProg2: POINTER TO FRAME[XProg2] =
except that these constant frame pointers will be filled
by the Mesa binder. (However, the declaration for XProg2 could not actually be
written as a valid Mesa statement because of the ambiguity inherent
in the two occurrences of XProg2 in
it.)
Such imported program constants are the analogs of
interface records. More can be done with them than with program
types (just as one can access more with an interface record than with an
interface type). In particular, one can access variables and
procedures with a frame pointer (as well as the compile-time
constants to which a program type provides access). Also, one can execute the
module instance corresponding to a frame pointer using START and
RESTART (sec.
7.8.2) and create additional instances of it using NEW (sec. 7.8.1).
Accessing values in a program frame as described above
treats the frame as a record with its variables and its procedures
as its components. The price paid for such close coupling with a program
is that the importer must be recompiled whenever the program is.
7.4.3. Exporting interfaces and program
modules
A module can export
an interface if it provides PUBLIC procedures, signals, errors,
or variables whose names and types match those of interface elements
in a DEFINITIONS module.
In addition, the program can export itself as part of an
interface if its
name appears there with an appropriate PROGRAM type. In all these cases,
the compiler checks that the type of each exported element is assignment
compatible (sec. 2.3) with the type of the corresponding interface element.
A single program module need not provide implementations
for all the items in an interface. This allows two or more modules
to cooperate in completely defining an interface. In such a case, it is common
for each of the
cooperating modules to use interfaces elements provided by the others. It can
do so by importing and exporting the same interface.
7.4.4. IMPORTS in DEFINITIONS modules *
Recall from section 7.2 that a definitions module can
contain an ImportsList. One interface, say Defs2, must import another, Defsl, if Defs2 requires
access to a nonconstant component of the latter. e.g., to a
procedure Online or otherwise) or interface variable in Defsl. All interfaces mentioned in
the ImportsList of a DEFINITIONS module must be unnamed. Any
importer of Defs2 must
also import an unnamed instance of Defsl;
in establishing the final binding, all unnamed instances
are matched. For example:
Defs2: DEFINITIONS
IMPORTS Defsl = BEGIN
Proc2: PROCEDURE 1...1 =
INLINE
BEGIN
...
IF Defsl. var # r
THEN
Defsl.Proc[... ]:
END:
E• ND.
Prog: PROGRAM IMPORTS Defsl, Defs2. AnotherDefsl: Defsl =
BEGIN
D• efs2.Proc2[...]; --
expansion references Defsl.Proc, not AnotherDefsl.Proc
END.
Note
that Prog must
import an instance of Defsl, even
if it makes no other mention of it, and one instance of Defsl must be unnamed.
7.5. Controlling module interfaces: PUBLIC and
PRIVATE
Every name defined in a module possesses an Access attribute,
either PUBLIC or
PRIVATE (the
module in which a name is defined is called its home module). These are used to
determine whether a name may be referenced when its home module is
included by some other module. A PUBLIC name can always be used: a PRIVATE name
cannot generally be used, except by modules which specify
that they SHARE the
included (PROGRAM or
DEFINITIONS) module.
The former modules are called non-privileged modules, and the latter are called privileged modules. A
variable's home module is, of course, privileged
Generally speaking. an Access may be
specified
(a) anywhere
a name can be declared. This includes normal declarations, named field lists
(for records or parameter lists), preceding, SELECT in
a record's variant part, and the declaration for an actual tag
in a variant part.
(b) preceding
the TypeSpecification in a type definition. In
addition. an
Access may be specified
(c) at the beginning of a module (the GlobalAccess),
to provide a default Access for any identifier in that module when one is not given explicitly for
the identifier.
The syntax in the following section is intended
to supersede earlier definitions of the same constructs only
by showing where attributes may be inserted. Otherwise, the earlier versions
are correct. Each syntax definition is followed by examples of its use.
7.5.1. Access attributes in
declarations
The
following three subsections deal with the placement of Access options in
declarations, field lists, and in variant records.
7.5.1.1. Declared names
"lbe form of Declaration specifying an Access
for its declared names is as follows:
Declaration :: = IdList : Access TypeSpecification
Initialization
Examples:
ql, q2: PUBLIC INTEGER 4-
0:
Mine: PRIVATE TYPE = {yes, no, maybe}:
Mine can only be used in (i.e.,
seen from) privileged modules. To non-priviliged modules it is not visible
at all.
7.5.1.2. Names specified in field
lists
The forms for specifying Access in a NamedFieldList (sec.
3.4.1) are as follows:
NamedFieldList
IdList : Access
FieldDescription
NamedFieldList . IdList : Access FieldDescription
1:
A non-privileged module could only access components a, c, and d in this case, and then only
using qualified references such as blk.a Within
a non-privileged module, extractors and constructors cannot
be employed for a record type with any PRIVATE components.
7.5.1.3. Names for variant parts and for tags in
variant records
 The forms for specifying
The forms for specifying
VariantFieldList
CommonPart VariantPart
Tag
TagType
Access in a VariantFieldList or Tag (sec. 6.3.1) are as
follows:
=
CommonPart
identifier : Access VariantPart I VariantPart
NamedFieldList
UnnamedFieldList
empty I NamedFieldList
SELECT Tag FROM
VariantList --
same as in sec.
6.3.1
ENDCASE
identifier : Access TagType
COMPUTED TagType
TypeSpecification I*
Example:
VarRec: PUBLIC TYPE = RECORD
link: POINTER TO VarRec, --
public common component
vpl: SELECT tgl: PRIVATE Etype
FROM -- public
variant. private tag
adjl =>
youGet:
Thisl tem,
iGel: PRIVATE SELECT tg2: * FROM --
a private variant part
• •
ENDCASE
adj2 =>. . .
ENDCASE
1:
Suppose a non-privileged module has a record of type VarRec. Then it could access variant
part vpl but
neither tag tgl nor
variant part iGet. This
only prevents it from referring to tgl
by qualification; it may still use a discriminating SELECT (which
implicitly accesses tgl) for
records of type VarRec. Thus,
an adjl arm
of such a WITH...SELECT
could access component you Get. However, it would be unable
to access component iGet in
any case.
Notice that the only way that the tag of a variant can be
changed is by writing a variant constructor (sec. 6.3.3).
7.5.2 Access
attributes in TYPE definitions
The form for
specifying a Typeldentifier whose defined type has an explicit Access
is as follows: Declaration :: = I IdList : TYPE = Access
TypeSpecification
Example:
OurType: PUBLIC TYPE =
PRIVATE RECORD[comp/: INTEGER, comp2:
BOOLEAN];
A non-privileged module could declare records of type OurType, but it could not access the
record components. The module could, however, pass values of type
OurType as
parameters. receive them as results from procedures, and use them as
operands of a fundamental operation (+-. =, #).
The Access in this form could be specified as PUBLIC, but
this would be pointless (if OurType
is PUBLIC then its type would be PUBLIC by
default; if OurType is
PRIVATE then
its type attribute is irrelevant). Note: Only names specified within the
defined type are affected by this form of attribute specification.
Consequently, it is intended for use only when defining record types and is just
a factorization: the PRIVATE
could have been written after each inner colon; also,
specific fields can be made accessible by writing PUBLIC internally,
as shown below:
AlmostPrivateType: PUBLIC TYPE =
PRIVATE RECORD
compl: PUBLIC INTEGER, -- overrides outer PRIVATE comp2: BOOLEAN
7.5.3. Default global access
If. as in section 7.4.1, a declaration specifies
an Access for
a name. then that unilaterally determines its Access. If not. the given item
recei\ es a default Access. The default may he specified
by the programmer in the GlobalAccess
for a module: otherwise one is assumed (for a
program module.
the normal default is PRIVATE.
for a DEFINITIONS module. it is PUBLIC). For
example,
.1//: PROGRAM = PUBLIC -- specified
GlobalAccess
BEGIN
• • •
END.
M3: PROGRAM = --
PRIVATE (by default)
BEGIN
END.
7.5.4. Accessing the PRIVATE predefined symbols of other modules *
A module may be privileged to use PRIVATE items
in an included module by using a Shares clause:
this contains a list of the (included) module names whose PRIVATE symbols
it needs to access. Consider the Friendly module below:
DIRECTORY
SpecialDefs:
FROM "specialdefs", StandardDefs:
FROM "standarddefs", PrivateDefs: FROM "private";
Friendly: PROGRAM SHARES PrivateDefs, SpecialDefs =
BEGIN
END.
In this case. Friendly
can use PRIVATE symbols defined by PrivateDefs and SpecialDefs but not the PRIVATE symbols
of StandardDeji There
is no particular significance to the ordering of module names
listed after SHARES. Any
kind of module may use SHARES
(but it ought to be one that is "friendly".
to say the least).
7.6. The Mesa configuration
language, an introductory example
This section discusses C/Mesa, the Mesa configuration language,
first by example, and then more rigorously by syntactic
definition and detailed semantics. It ends with a number of detailed examples
which explore some of the more intricate parts of C/Mesa.
We first present an
example consisting of three Mesa modules: An interface (a DEFINITIONS module),
an implementor for it (a PROGRAM module),
and a client for the implementation (also a PROGRAM module).
The example is presented here to show the
relationships among definitions, implementors, and clients.
Following it will be a sequence of example configurations for systems
constructed from this implementor and client. The line numbers in the
left margin are provided for ease of reference and are
not part of the source code. First the interface:
dl: LexiconDefs: DEFINITIONS =
d2:
BEGIN
d3:
FindString:
PROCEDURE
[STRING] RETURNS [BOOLEAN]:
d4:
AddS/ring: PROCEDURE [STRING]:
d5:
PrintLexicon:
PROCEDURE;
d6: END.
7.6.1. Lexicon: a module implementing Lexiconnefs
The following module (Lexicon) implements
the LexiconDefs interface. That is,
(a) Lexicon declares PUBLIC procedures
FindString, AddString, and
PrintLexicon, which
have procedure types conforming to their counterparts in the DEFINITIONS module;
(b) Lexicon EXPORTS the interface LexiconDefs.
Lexicon IMPORTS three interfaces: SystemDefs, 10Defs. and
StringDefs. The
USING clauses
of the DIRECTORY note
which procedures are defined in each.
Details on these and other Mesa system interfaces are
contained in the Mesa System Documentation.
The code for Lexicon
follows. For reading convenience, any references to
procedures from imported interfaces are in boldface.
DIRECTORY
i2:
10Defs:
FROM "iodefs" USING [WriteLine],
i3:
LexiconDefs:
FROM "lexicondefs",
i4:
StringDefs:
FROM "stringdefs"
USING [Appet2dString],
i5:
SystemDefs:
FROM "systemdefs"
USING [AllocateHeapNode, AllocateHeapStrind
i6:
i7:
Lexicon: PROGRAM
i8:
IMPORTS SystemDefs, 10Defs,
StringDefs
i9:
EXPORTS LexiconDefs =
110:
ill: BEGIN
i12:
113: Node: TYPE = RECORD [!link, rlink: NodePtr, siring:
STRING]:
i14:
NodePtr:
TYPE
= POINTER TO Node:
i15:
Comparative:
TYPE = lessThan, equalTo. greaterThattl:
i16:
117: mot: NodePtr NIL:
i18:
i19:
FindString:
PUBLIC PROCEDURE [s:
STRING] RETURNS
[BOOLEAN] =
120: BEGIN RETURN [SearchForString[root, 5]]: END:
i21:
122: .S'earchForString: PROCEDURE [n: NodePtr, s: STRING]
i23:
RETURNS [found: BOOLEAN] =
i24:
BEGIN
i25: IF n =
NIL THEN RETURN
[FALSE]:
126: SELECT LexicalCompare[s.
n.siring] FROM
i27:
lessThan =>
found SearchForString[n.11ink, s]:
i28:
equalTo =>
found +- TRUE:
i29: grealerThan => found 4- SearchForString[n.rlink, s]:
130: ENDCASE:
i31:
RETURN [found]:
i32:
END: i33:
i34:
AddString:
PUBLIC PROCEDURE
[s: STRING] =
i35:
BEGIN InsertString[row. s]:
END;
136:
i37:
insert.S7ring: PROCEDURE [n: NodePtr. s: STRING] =
i38:
BEGIN
i39: .VewNode: PROCEDURE RETURNS [n: .VodePtt] =
140:
BEGIN OPEN SystemDefs:
141:
n 4-
AllocateHeapNode[sizE[Node]]:
142:
trt 4-
Node[string: AllocateHeapString[s.lengq. !link: NIL. rlink: NIL]:
143:
.S.tringDels.AppendString[n.string.
s]:
i44: RETURN;
145: END;
i46:
i47:
IF 11 = NIL THEN root 4-
NewNode [ --
then just return
i48:
ELSE
i49:
SELECT LexicalCompare[s,
ti.string] FROM
150:
lessThan =>
IF talink # NIL THEN InsertString[n.11ink.
s]
151:
ELSE allink NewNode[];
152:
equal
To => NULL; --
already there: just return
153:
greaterThan
=> IF n.rlink # NIL THEN InsertS tring[n.rlink, s]
154: ELSE arlink 4- NewNode[];
i55: ENDCASE;
156: END;
i57:
158:
LexicalCompare:
PROCEDURE
[il, s2: STRING] RETURNS [c: Comparative] =
159:
BEGIN
160:
n: CARDINAL = MIN [sl.length, s2.1ength];
161:
i: CARDINAL;
i62: FOR i IN [0..n) DO
163: SELECT LowerCase[sl [1]] FROM
i64:
<LowerCase
[s2 [i]] => RETURN
[lessThan]:
i65:
>LowerCase[s2
[i]] => RETURN
[greaterThan];
166: ENDCASE;
i67:
ENDLOOP;
i68:
C 4- SELECT sl.length FROM
i69:
<s2.1ength => lessThan, is
shorter than s2
i70:
>s2.length => greaterThan, sl
is longer than s2
171: ENDCASE =>
equalTo; --
lengths are the same
i72:
RETURNICI:
i73:
END;
i74:
i75:
lower. PACKED ARRAY CHARACTER[A .. 7] OF CHARACTER =
i76:
['a,'13,'c2d2e,'Ugs'h,.1,J,'k,'1,'m,'n;o.'p,'q,'r,'s,'Cu,'
V w,'x2y,'z]:
i77:
i78:
LowerCase:
PROCEDURE [c: CHARACTER] RETURNS [CHARACTER] =
i79:
BEGIN RETURN [IF C IN [A..7] THEN lower[c] ELSE
c]; END;
180:
![Text Box: PriniLexicon: PUBLIC PROCEDURE = BEGIN PrMtNode[root] END:](23a-MesaManualOCR_files/image068.gif)
181:
182: i83:
185:
![Text Box: PrintAlode: PROCEDURE[n: NodePtr] =- BEGIN
IF n = NIL THEN RETURN;
PrintNode[ialink];
10Defs.WriteLine[n.string]; PrintNode[n.rlink];
END; END.](23a-MesaManualOCR_files/image069.gif)
186:
i87:
i88: i89:
190:
191:
7.6.2. LexiconClient:
a client module
The module, LexiconClient, below is a client for Lexicon and IMPORTS LexiconDefs. It is also a client
for the interface 10Defs (and
also uses the constant CR defined
in 10Defs in
section 7.1). the program provides a simple terminal interface to a
user for testing Lexicon.
cl: DIRECTORY
c2:
10Defs:
FROM "iodefs"
USING [CR. ReadCha4, ReadLine, WriteChar. WriteLine],
c3:
LexiconDefs:
FROM "lexicondefs"
USING [AddString. lind.S"tring, PrintLexicon];
c4:
c5:
LexiconClient:
PROGRAM IMPORTS 10Defs, LexiconDefs =
c6:
c7:
BEGIN OPEN 10Defs, LexiconDefs:
c8:
c9:
s: STRING f
[80]:
c10: ch: CHARACTER;
cll: DO -- loop until stopped by user
typing q or Q (last case below).
c12:
WriteChar[CR];
WriteLinerLexicon Command:
"1:
c13:
ch ReadChar[];
c14:
WriteChar[ch];--
Echo the character (ReadChar doesn't).
c15:
SELECT
ch FROM
c16:
'f, 'F =>
c17:
BEGIN
c18:
WriteLinerind:
"1; -- terminal will read:
"find: "
c19:
ReadLine[s]; s
will contain the string read from the terminal
c20:
IF FindString[s] THEN WriteLine[" -- found"]
c21:
ELSE WriteLiner -- not
found"]:
c22:
END;
c23:
'a, 'A =>
c24:
BEGIN
c25:
WyiteLinerdd:
"I; --
terminal will read: "add: "
c26:
ReadLine [s];
c27:
AddString [s];
c28:
END;
c29:
'p, 'P = >
c30:
BEGIN
c31:
WriteLine["rint lexicon"]: -- terminal will read:
"print lexicon"
c32:
WriteChar[CR];
PrintLexicon[];
c33:
END:
c34:
=>
c35:
BEGIN
c36:
WriteLine["
uit"]; WriteChar[CR]; -- terminal
will read: "quit"
c37:
STOP;
c38:
END;
c39:
ENDCASE = > WriteLine[" Commands are Find, Add,
Print lexicon, and Quit"];
c40:
ENDLOOP;
c41:
c42: END.
7.6.3. Binding, loading, and
running a configuration: an overview
A configuration
description, a "program" written in C/Mesa,
describes how a set of Mesa modules are to be bound together to
form a configuration. This binding is accomplished by "compiling" the
configuration description (or, configuration for short) and results in a binary configuration description (a BCD).
The simplest (or atomic) BCD is the object module for a Mesa program module. Thus,
the Mesa compiler produces the simplest BCDs. and the C/Mesa compiler (also
called the Mesa Binder) produces complex BCDs from simpler ones. Indeed,
a configuration may combine both atomic and non-atomic BCDs together
into a single, new BCD. For these reasons, the object modules produced by
the Mesa compiler have the same form of names as the output of the Binder.
i.e., names of the form "BasicName.bcd".
Once a BCD has been created, it can be loaded and run.
Loading is a sequence of two actions. The first makes an instance of the configuration
by allocating a frame for each atomic module in the BCD. Each
frame has space for the module's static
variables (those declared in the main body of the module)
and some extra space for information used by the Mesa system.
Imported procedures and variables are accessed via links. Space for these links is allocated
either in the frame or in the code of the module.
The second part of loading completes the binding
process by filling in the links for each module instance in the
configuration instance. Some of these links will "point to"
procedures and variables in the same configuration. Others will
"point to" procedures and variables in the running system in which
the configuration is being loaded.
Once a configuration is loaded, each module instance in it
has all its interfaces bound. However, no code has been executed in
the instances, so global variables are not initialized, and no mainline statements
have executed. sTAR-ring (sec. 7.8.2) an instance executes any code for
initializing static variables and also executes its mainline code.
For correct operation. this must occur before any of its
procedures are used or before any of its global variables are referenced. If a
module is not explicitly STARTed before one of its procedures
is called, then a trap occurs, and it is automatically started.
Once it STOPS (sec.
7.8.2), the procedure call is allowed to proceed. Subsequent procedure calls
will not repeat this trap and auto-initialization sequence. Section 7.8 details
how these mechanisms generalize for configurations.
7.6.4. A configuration description
for running LexiconClient
The following configuration will bind Lexicon, LexiconClient, and
other necessary modules and can be used to start the client
program running. The comments to the right of each module name indicate
which interfaces are imported and exported by that particular module: they are
not part of Configl . This
configuration is completely self-contained:
all the needed imports are satisfied by interfaces
exported from modules which are part of the configuration.
Configi:
CONFIGURATION
CONTROL LexiconClient = BEGIN
Fsp: EXPORTS
SysiemDefs
10Pkg: EXPORTS
10Defs
Strings: EXPORTS
StringDefs
Lexicon: IMPORTS SystemDefs,
10Defs. StringDefs EXPORTS LexiconDefs
LexiconClient: IMPORTS IODefs,
LexiconDefs
END:
To see that this configuration is completely
self-contained, notice that LexiconClient
imports IODefs,
which is exported by 10Pkg, and imports LexiconDefs, which is exported by the instance of Lexicon. Similarly. the other
instances' import requirements are satisfied by some exported interface in Configl
7.7 C/Mesa: syntax and semantics
'Ihe following is the complete syntax
for C/Mesa. It hears strong resemblance to Mesa itself, but this
grammar describes a completely separate language. A phrase class
beginning with a C indicates a syntactic unit that is
unique to C/Mesa. All the other units have the same syntax (but not necessarily
exactly the same semantics)
as they do in Mesa itself.
ConfigDescription = CDirectory -- optional
CPacking
Configuration . -
note the final period
CDirectory = --
same as in Mesa. only no USING clauses
Configuration = identifier : CHead =
CBody
CExports empty I
EXPORTS ItemList
CExpression CPrimary I CExpression
THEN CRightSide
CLeftSide Item I [ ItemList
CBody BEGIN CStatementSeries
END
CHead CONFIGURATION CLinks Imports CExports ControlClause
ControlClause CONTROL identifier I empty
CLinks empty
I LINKS : CODE I LINKS
: FRAME
CPacking empty I
CPackSeries ;
CPackList PACK IdList
CPackSeries CPackList I CPackSeries ;
CPackList
CPrimary CRightSide
I CPrimary PLUS CRightSide
CRightSide Item I Item []
CLinks I Item [ IdList CLinks
CStatement CLeftSide
CExpression
CRightSide I
Configuration
CStatementSeries = CStatement
CStatementSeries I
CStatementSeries ;
CStatement
Imports =
empty I
IMPORTS ItemList
Item = identifier I identifier : identifier
ItemList = Item I ItemList , Item
We will use the term "component" to refer to the
parts of a configuration; i.e., for both atomic modules and
configurations containing several modules. When necessary, the kind of
component will be expressly given.
Similarly. we will use the term
"interface" to stand for an interface record or a module instance (if
used in discussing imports or exports), and we will
distinguish as necessary. However, "interface" will
never include or imply the term ''interface type" (sec. 7.4.1).
Lastly, we will
need to distinguish between instances of components and their prototypes (the
BCD files) from which such instances are made. Hence, a program prototype is
the BCD file for a Mesa program module, and a configuration prototype is the analog for
configurations. If the term
prototype is used by itself, it includes
both cases.
The
CPacking and CLinks clauses
in the syntax are directives to the Mesa Binder. CPacking identifies modules whose
code should be packed together for swapping purposes. CLinks specifies
for
a module or a configuration whether links to imported interfaces should be
stored in the-frame or in the code. The use and implications of these
optional clauses is described in Appendix D.
7.7.1. IMPORTS, EXPORTS, and DIRECTORY in C/Mesa
For completely self-contained, simple configurations like
Configl. a
configuration description is primarily just a list of
component names. An instance of each named component will be part of the configuration.
and if a component imports any interfaces. they will be supplied by those
exported from other components of the configuration.
Configurations need not be self-contained.
however, and may themselves import interfaces to be further
imported by their components. In this way. subsystems can be constructed with
some imported interfaces unbound. Loading such a
configuration or naming it as a component in another configuration will supply
the necessary interfaces. Furthermore, a configuration can make exported interfaces
available for importation by other modules and configurations. For example, the
interfaces SystemDefs,
10Defs, and StringDefs needed by Configl would normally be supplied
by a pre-existing Mesa system configuration. Therefore, it is
really not necessary to include instances of Fsp, IOPkg, and Strings in Configl. Instead, it can just import
them:
c2.1: Conjig2: CONFIGURATION
c2.2: IMPORTS SysteinDefs, 10Defs, StringDefs
c2.3: CONTROL LexiconClient
=
c2.4: BEGIN
c2.5: Lexicon;
c2.6: LexiconClient;
c2.7: END
The imports clause in a configuration serves the same
purpose as in a program module. The rule for importing is: If some
component named in a configuration imports SomeDefs, and SomeDefs
is not exported by a component in the
configuration, then it must be imported. For example, SystemDefs did not have to be
imported into Configl, but
it did have to be imported into Config2.
The rule for exports is simpler: If a component
in a configuration exports an interface, that interface may also
be exported another level from the configuration. It is not required that it be exported,
however. This important feature enables one to control what is exported from a configuration and what is to be hidden from external view.
None of the example configurations given so far have had a
DIRECTORY section.
This is because the default association of a component named Prog is to a file named
"Prog.bcd" in which the ModuleName is also
Prog. Since
this is often the case, the programmer normally does not need CO supply one. A DIRECTORY part
would be needed if the file did not have such a defaultable name. For
example:
DIRECTORY
Frog: FROM "OldProgFile";
could not be omitted if the component named Prog is contained in the file
"OldProgFile.bcd", rather than in "Prog.bcd".
7.7.2 Explicit naming, IMPORTS, and EXPORTS *
In Mesa, names may be given to the interface
records in an IMPORTS
list (sec. 7.4.1); the same is true in
a configuration description. These names can then be used to supply the
interfaces needed by component instances in the configuration. The
notation for explicitly supplying interfaces to a
component is similar to that for parameter lists
in Mesa (except that there is no keyword notation for explicit
imports parameter lists). For example. lines c2.1 through c2.5 above could have
been written as
|
c2a.1: Oa): c2a.3: c2a.4: c2a.5:
|
Config2A: CONFIGURATION IMPORTS allot: SysteniDefs. CONTROL LexiconClient =
BEGIN
Lexicon [allot. io, str]:
|
io: IODefs,
str: StringDefs
|
The interfaces listed after Lexicon must correspond in order and
(interface) type with the IMPORTS list for Lexicon (look at Lexicon in sec. 7.6.1 to check
this).
A name may also be given to each component instance in a
configuration by preceding the instance with "identifier :". This
facility is necessary to distinguish multiple instances of the same prototype
from one another. For example, we could name the Lexicon instance in line c2a.5 as follows:
alex: Lexicon[alloc,
io, str];
Lexicon exports
an interface whose type is LexiconDefs,
and that interface record can also be named. The
following further
modification to line c2a.5 names it lexRec:
lexRec: LexiconDefs alex: Lexicon [allot, io,
sir];
Here, as in Mesa, the type of lexRec follows the colon in the
declaration, and lexRec is
assigned the (single) interface exported by Lexicon. However,
the type LexiconDefs is
not actually necessary (it is
inferred from Lexicon's EXPORTS list), and the line
could have been
shortened to
lexRec alex:
Lexicon[alloc, io, sir];
Using all these explicit naming
capabilities, we can now write a new version of the configuration in which
none of the C/Mesa default naming is used:
c3.1: Config3: CONFIGURATION
c3.2: IMPORTS allot: SystemDefs, io: IODefs, StringDefs
c3.3: CONTROL lexClient
=
c3.4: BEGIN
c3.5: lexRec: LexiconDefs alex: Lexicon [allot, io,
sir];
c3.6: lexClient: LexiconClient[io, lexRec];
c3.7: END.
An exported interface like lexRec need not always be set as
the result of including a component instance like alex in the configuration. One
can also assign interface records to one another as in
the following two (equivalent) lines:
anotherLexRec:
LexiconDefs 4- lexRec: anotherLexRec
4- lexRec;
The form of CRightSide in these two statements only copies lexRec, whereas ones like line c3.5
above involve a "call" on a component prototype. The result of that
''call" is an instance of the component, and a set of
results, the interface records exported by it.
7.7.3. Default
names for interfaces and instances *
A component instance that is not explicitly given a name
is given a default name equal to the name
of the component prototype.
Thus, the body of Config2 is
treated as if the programmer had written:
BEGIN
Lexicon: Lexicon:
LexiconClient: LexiconClient:
END.
Similarly.
an unnamed interface is given a default name equal to the name of its interface
type. So. another equivalent body for Config2 is
BEGIN
LexiconDefs: LexiconDefs Lexicon:
Lexicon[]:
LexiconClient: LexiconClient:
END.
The empty imports parameter list in "Lexicon H" specifies
that a new instance of the prototype Lexicon is to be created. If the empty imports list were
not there, the binder would interpret the appearance of Lexicon (the one after the colon) as
the name of an already existing interface (riot of an already existing module
instance). When no assignment is specified, the empty imports parameter
list is not necessary, as shown in the earlier examples.
Normally, omitting an imports parameter list (or.
equivalently, specifying an empty list) means that the binder should use the
default-named interfaces needed by that component instance. Thus, we could
rewrite a
completely explicit (and very wordy, but equivalent) version of Config2:
c2x.l: Config2X: CONFIGURATION
c2x.2: IMPORTS SysternDefs: SysteniDefs, IODefs: IODefs,
StringDefs: StringDefs
c2x.3: CONTROL LexiconClient
=
c2x.4: BEGIN
c2x.5: LexiconDefs: LexiconDefs 4- Lexicon:
Lexicon [SysteniDefs, IODefs, StringDefs];
c2x.6: LexiconClient: LexiconClient [IODefs,
LexiconDefs];
c2x.7: END.
Notice that the defaults greatly simplify a
configuration, but that they also obscure a great deal of machinery
concerned with naming things. It is important that the programmer not
completely forget these details. Otherwise one could commit errors
by not distinguishing between interface records and interface
types, or between component instances and prototypes. For instance, this could
be a problem if there are multiple component instances.
Therefore, one is well advised to assign unique names to the instances.
7.7.4. Multiple ex-ported
interfaces from a single component *
A component can export more than a single
interface. Assigning these exported interfaces to interface
records is done using a Mesa-like extractor (sec. 3.4.5). For
example, if we had a program module .S'IringsAnc110 that exported both StringDefs and IODefs, we could use it in a
modified Config2 as follows:
c4.1: Config4: CONFIGURATION
c4.2: IMPORTS alloc:
SystemDefs
c4.3: CONTROL LexiconClient
=
c4.4: BEGIN
c4.5: [str: .StringDefs, io: IODefs] StringsAnd10[];
c4.6: Lexicon[alloc. io. sir]:
c4.7: LexiconClient [io, LexiconDefs];
c4.8: END.
Line c4.5 assigns the
exported interfaces obtained by instantiating StringsAnd10 (that is why it has
an explicit. although empty imports parameter
list following it) and declares their types as well. It would
he equally correct
to write instead
[sir StringsAnd10
In this case the types for io and sir would be inferred from the
types of the interface records exported by StringsAnd10. However,
if the programmer had written instead,
[io. sit] .S.tringsAnd1011:
with the positions of io and str
reversed, that would have been accepted, but would have
caused errors in both lines c4.6 and c4.7 because their inferred
types would not match those explicit imports parameter lists. Be cautious when doing this.
Default names could also have been used for the exported
interfaces in line c4.5, and Config4
could simply have been written
as
c4a.1: Config4 A: CONFIGURATION
c4a.2: IMPORTS SystemDefs
c4a.3: CONTROL LexiconClient
c4a.4: BEGIN
c4a.5: StringsAnd10:
c4a.6: Lexicon:
c4a.7: LexiconClient:
c4a.8: END.
This would assign the exported interfaces to the
default-named records StringDefs and
IODefs and
would use them in the defaulted import parameter lists
for Lexicon and
LexiconClient. Line
c4a.5 could also show what StringsAndlO exports using the default names for its exported
records. This
would give rise to the statement:
[StringDefs, 10Defs] StringsAndlO El:
Cases
like this require that the user be aware of the distinction between interface
records and interface types: StringDefs names an interface record here, but in line
c4.5, it names an interface
7.7.5. Multiple components
implementing a single interface *
An exported interface can be the result of
contributions by a number of components. Think of the interface
as a logical unit that may be implemented by a number of cooperating physical
units (i.e.. modules and configurations). For example, assume that Lexicon is divided into two modules LexiconFA and LexiconP. with LexiconFA providing the procedures FindString and AddString, and LexiconP providing PrintLexicon. Each exports LexiconDefs, but neither fully
implements that interface. Still. LexiconClient
will see a single interface in the following:
c5.1: Config5:
CONFIGURATION
c5.2: IMPORTS SystemDefs. 10Defs, StringDefs
c5.3: CONTROL LexiconClient
=
c5.4: BEGIN
c5.5: lexRec: LexiconDefs LexiconFAH: --
use default imports
c5.6: lexRec LexiconP[]; --
merge interface contributions
c5.7: LexiconClient[I0Defs,
lexRec]:
c5.8: END.
The two separate assignments to lexRec above actually merge the
interface elements exported by the two modules. This merging
does not allow any duplication of elements, and if both modules exported
PrintLexicon, for
example, an error would be generated during processing of Config5 by
the Binder.
The user may control the
merging of interfaces himself using the PLUS operator. To obtain the same effect
as above (but by explicit specification). one could write

If
the programmer wanted to use the original Lexicon. but use LexiconPs PrintLexicon in
the interface instead of Lexicon's, he could use the THEN operator:
|
lexRec *- Lexicon[];
lexRecP LexiconP[];
lexRecNew 4- lexRecP THEN lexRec;
LexiconClient[10Defs, lexRecNew]:
|
-- defines a complete interface -- defines one procedure
-- this order is important
|
The THEN operator makes an interface that includes all the elements
defined by lexRecP (the
left operand) together with those from lexRec (the right operand) that do
not duplicate any in lexRecP. This
could be useful if one simply wanted to test a new version of PrintLexicon procedure without altering
Lexicon itself
during the debugging period. Also. one could use THEN to provide a number of
alternative PrintLexicon procedures,
with the standard one incorporated in Lexicon.
7.7.6. Nested (local) configurations
Configurations may be defined within configurations, much
like local procedures (sec. 5.7) may be defined within other procedures in
Mesa. They can then be instantiated and parametrized, and they can
export interfaces (just like any configuration).
Nested configurations can be used to hide some of the
interfaces exported by components in a configuration. For example,
suppose that multiple instances of some component ProgAlod were needed in a
configuration, and further suppose that ProgMod exports the interface ProgDefs. Even if
none of the exported ProgDefs interface
records are needed in the configuration, they would each have
to be given a unique name to avoid an interface merging error (sec. 7.7.5).
This could be avoided by
defining the following
nested configuration:
NonexportingPM: CONFIGURATION
= BEGIN
ProgAlod END.
Using NonexportingPM
in place of ProgAlod
avoids the duplicate interface problem because the local
configuration does not export the interface ProgDefs produced by instantiating ProgMod within it.
Nested configurations can also be used to avoid
writing sequences of C/Mesa statements more than once. By collecting
such a sequence in a nested configuration, one can get the effect of writing
the whole sequence simply by instantiating the configuration.
The scope rules for names in C/Mesa allows a nested
configuration to access interfaces and other (also nested)
configurations outside it. So, one configuration can make instances of others. However,
in its IMPORTS list,
a nested configuration must name any interfaces that its components import
but which are not satisfied within it. That is, interfaces are never
automatically imported into a nested configuration.
7.8. Loading modules and configurations
This section describes how configurations are
loaded and run. Simple. atomic modules are discussed first,
and then more general configurations.
Loading and running an atomic module is a sequence of
four actions:
(1)
loading its object code (from the .13CD file),
(2) allocating
a frame for its static variables,
(3) filling
in procedure descriptors for imported procedures and frame pointers for
imported modules,
(4)
initializing the module's variables and executing
its mainline code.
Actions (1), (2). and (3) are acomplished by system
procedure, documented in the System Documentation. Action (4) can be
accomplished by explicitly starting the instance or by means of a trap
on the first call to any of its procedures (both of these methods are described
below).
7.8.1. The NEW operation for making copies of modules The
syntax for the NEW operation is
Expression ::= I NEW
Variable
The Variable may
be the name of an imported frame pointer, a pointer to the frame of a program module,
a program variable, or the module name of the module containing the NEW statement. For
example:
proglnsil,
progl nst2: POINTER TO FRAME [Nog];
• • •
progInst2 n- NEW progl
The new instance is only a copy of the frame insofar as
its interface records are concerned. In all other respects it
is uninitialized, just like a new instance. In particular, it must be started
to supply its program parameters (if any) and to initialize its
global variables. At the time the copy is made, it will
have exactly the same bindings as the original. If some of the globally
available interface records maintained by the loader (sec. 7.8.2)
later change, the copy may be bound differently than the
original.
If a module imports a program
Pimpl (sec.
7.4.2), the operation "NEW Pimp)"
copies Pimp'.
A program module's type may be declared in a definitions
module in the same way as a procedure's type is. Such a defined
program is part of the interface defined by that definitions module and may, therefore,
be imported by another module as part of that interface. Then, copies of that
module can be made using the NEW operation. For example, assume that the following
declaration appears in the definitions module, Defs:
ExportedProg: PROGRAM [i: INTEGER]:
Any program that imports Defs will then have access to a
value named ExportedProg which
will have been bound (in step
(3) of the loading process) to an instance of a program whose parameter types
conform with those of ExportedProg.
The only operation that a program can perform using this
value is to START it, RESTART
it, or make a copy of it using "NEW ExportedProg". In
summary, a program imported as part of an interface behaves like a
value that is a pointer to a frame.
If a program, say Prog. wishes
to create a copy of itself,
it can say:
copy: POINTER TO FRAME [Frog]:
copy NEW Prog:
7.8.2. How
the loader binds interfaces
Each instance of an atomic module or of a configuration may export
some interfaces. To make these exported interfaces available for
importation by other instances, the loader maintains a single. simple
global table of all the exported interfaces. If any duplicates are created as
the result of a NEW, they
are merged into the already existing interface records as if a THEN (sec. 7.7.5) had
been done.
The moral here is that complicated binding to hide
interfaces. etc. must be done using the binder, and only the
simplest, most straightforward forms should be used at loading time. ,
-
7.8.3. STARTing, STOPping, and RESTARTing module instances
The START operation suspends the execution of the program or
procedure executing it and transfers control to a new,
uninitialized instance of an atomic module. Additionally, if the program
instance being started requires parameters, they are supplied as
part of the START. Similarly,
if the program being started is specified
to return results (more details below), then the START operation may appear in
a RightSide context, and the returned value is the value of the
operation. Its syntax is
StartStmt =
START
Call I ...
StartExpr = START Call I ...
The variable following the word START must
represent a global frame pointer or program variable: i.e.,
its type must conform to some POINTER TO FRAME type or PROGRAM type. Here are some examples
of its use:
START proglnst:
START ExportedProg [5 -FA:
x 4- START progWithResult
VirstArg: a, secondArg: bl: --keyword
parameter list
When a program is started. it first executes code to
initialize any static variables that were declared with
initialization expressions. The initializations are done in the order in which
the variables were declared in the program. Also, they
may call both local and imported procedures (since descriptors for
all imported procedures are filled in as part of the NEW operation - sec.
7.7.1).
After all initialization expressions are complete. the
mainline statements of the program commence executing. Control
can then return to the caller (the program or procedure which initiated the START) in
one of two ways: the started program may STOP or it may RETURN with results (however, it
cannot use both).
A program that executes a STOP can be RESTARTed later. RESTART is
distinct from START
primarily because it cannot pass parameters as START can.
If a program does not return results, it either by an explicit
use of STOP or by
running off the end of the program.
If a program declares (in its ModuleHeader) that
it returns results, it uses RETURN statements just as does a procedure (and it
cannot use STOP). A
RETURN from
a program does not deallocate
its global frame. The syntax for RESTART and STOP is
RestartStmt = RESTART Variable
I
StopStmt = STOP I
The Variable following RESTART must be a pointer to the
frame for a program instance or a program variable, just as
for START. A
program that RETURNS results
or has run off the end cannot be RESTA.RTCd. Attempting
to do so will result in a run time error.
A module instance can also be STARTed "automatically".
If a call is made on a procedure in an instance that has not yet
been started, a start trap occurs.
If the module does not take parameters when started. then it is
started by the Mesa start-trap handler. When it STOPS or RETURNS, the
trap handler completes the procedure call that was in progress
when the trap occurred. (See the next section for further discussion of the start trap for
configurations.)
Warning:
A module must be STARTed either explicitly or implicitly before any attempt is
made to access its variables through a POINTER TO FRAME.
7.8.4. Loading and starting
configurations
By using system routines, one can also make instances of
configurations that are more than simple, atomic modules. A non-atomic
configuration cannot be STARTed (what would it mean to start one?),
but its CONTROL module
can (if it has one). Basically, the CONTROL module acts as the representative
for the whole configuration (since a C/Mesa configuration description does not contain
executable Mesa statements). Thus, a program that STARTS the
CONTROL module
for a configuration has essentially STARTed the
configuration. If the order of starting some of the instances
in a configuration is important or if they take arguments when started, its CONTROL module
should START them explicitly.
The start trap works for configurations as well
as for atomic modules. If a start
trap occurs for a module Al in
configuration C with control module cAf,
then the trap handler automatically starts cAl rather than Al, If the handler discovers,
however, that cAl has
already been started, it will start Al
(since cAl would
have started AI if it had intended to). In fact, if the handler starts tilt but still finds
AI unstarted
when a/ STOPS, it will
start Al itself
before finally returning from the trap. Then the procedure call that caused the trap will be allowed to go
through.
Fine
points:
If an
attempt is made to RESTART a program which has not been started, a
START trap will occur and then the RESTART will proceed.
Other forms of START and STOP
statements are used to catch signals. This is discussed in Chapter 8, but the forms look roughly as follows:
START
somelnstance[ ComponentList ! CatchPhrase I
STOP [ !CatchPhrasej
CHAPTER
8.
SIGNALLING AND SIGNAL DATA TYPES
Signals are used to indicate when exceptional conditions
arise in the course of execution, and they provide an orderly
means of dealing with those conditions, at low cost if none are generated (and they
almost never are). For example, it is common in most languages to write a
storage allocator so that, if asked for a block whose size is too large, it
returns a null (or otherwise invalid) pointer value. Any program
which calls the allocator then embeds the call in an IF statement, and checks the return value
to make sure that the request was satisfied. What that procedure then does is a
very local decision.
In Mesa, one would write the allocator as if it always returned a valid pointer to
an allocated block, and calls to it would simply assign the returned value to a
suitable pointer, without checking whether or not the
allocation worked. If the caller needs to gain control when the
allocator fails, the programmer attaches a CatchPhrase to the
call: then if the allocator generates the signal BlockTooLarge, and the caller has
indicated that it wants to catch that signal, it will.
This way of handling exceptions has two important
properties, one for the human reader of the program, and one
for its execution efficiency:
Anyone reading a program with a call on the
allocator can see immediately that an exceptional condition can
arise (by the catch phrase on the call or nearby): he then knows that
this is an unusual event and can read on with the normal program flow: IF statements do not have this
characteristic of distinguishing one branch from the other.
When the program is executing. the code to
check the value returned by the allocator on every call is not present and
therefore takes no space or execution time. Instead, if a signal is
generated, there is more overhead to get to the catch phrase than a
simple transfer: but since it happens infrequently, the overall efficiency is
much higher than checking each call with an IF statement.
Signals work over many levels of procedure call, and it
is possible for a signal to be generated by one procedure and
be handled by another procedure much higher up in the call chain. We later discuss
the mechanisms by which this is done: until then, examples show signals being
caught by the caller of the procedure which generated the
signal.
8.1. Declaring
and generating SIGNALS and ERRORS
In its simplest form, a signal is just a name for some
exceptional condition. Often, parameters are passed along with
the signal to help a catch phrase which handles it in determining what went wrong.
It is also possible to recover from a signal and allow the routine which
generated it to continue on its merry way. This is done by a
catch phrase returning a result: the program which generated
the signal receives this result as if it had called a normal procedure instead
of a signal.
-therefore,
from the type viewpoint, signals correspond \ ery closely to procedures: in
fact, the type constructor for declaring signals is just a
variation of the one for procedures:
SignaITC = SignalOrError
ParameterList RETURNS
ResultList I
SignalOrError ParameterList I
SignalOrError
RETURNS ResultList
SignalOrError
SignalOrError = SIGNAL I ERROR
For example. the signal BlockTooLarge might be defined to carry along with it two
parameters, a Zone within
which the allocator was trying to get a block, and the number of words needed
to fill the current request. The catch phrase that handles the
signal is expected to send back (i.e., return) an array
descriptor for a block of storage to be added to the zone. The declaration of BlockTooLarge would look like
BlockTooLarge: SIGNAL[?: Zone, needed: CARDINAL] RETuRNs[newStorage:
DESCRIPTOR FOR
ARRAY OF CARDINAL];
A signal variable contains a unique name at run time.
which is a code identifying an actual
signal, just as a procedure variable must be assigned an actual procedure before
it can be used. If a procedure is imported from an interface (sec.
7.4), any signals
that it generates directly are probably contained in the same
interface. Imported signals are bound by the same mechanisms as procedures. In
addition, one may have signal variables which can be assigned any signal value
of a compatible type.
The signal analog of an
actual procedure is obtained by initializing a signal variable using the syntax
= CODE" in
place of "= BEGIN...END"
for procedures. This causes the signal to be initialized
to contain a unique value. The following syntax describes the
initialization for an actual signal:
Initialization =
= CODE
A signal is generated by using it in a SignalCall as shown in the
syntax below:
Statement = SignalCall I ...
SignalCall = SIGNAL Call I ErrorCall
ErrorCall = RETURN WITH ERROR Call I
ERROR Call I
ERROR --
special error
Call is defined in section 5.4, and the called Expression must have some signal type
in this case. A SignalCall can
be used as an Expression as well as a Statement. For
example,
newblock <- SIGNAL BlockTooLarge[zone, n];
Thus, generating a signal or error looks just like a procedure
call, except for the additional word,
ERROR or SIGNAL.
Fine
point:
Although it is not
recommended, the keywords SIGNAL and ERROR may be omitted (except in the RETURN
WITH ERROR construct). This
makes the signal look exactly like a procedure call.
Initialization
by SIGNAL = CODE produces a unique value that contains. in part. the global
frame index of the module
containing the initialization. There are two points worth making.
If one creates a copy of the module with the NEW statement. signals raised •by the two copies will be
different. If
the signal is declared and
initialized in a
procedure, recursive calls of the procedure
will not generate different signal values.
If a signal is declared as an ERROR, it
must be generated by an ErrorCall. If,
however, it is declared as a SIGNAL. it can be generated by any SignalCall, including an ErrorCall. The difference
between the two is that a catch phrase may not RESUME a
signal generated by an ErrorCall (sec.
8.2.5).
Except for a slight difference in the way' the
error is started (sec. 8.2.3), the RETURN WITH ERROR construct behaves like the ERROR statement.
Its primary use is in monitor ENTRY procedures (chapter 10).
The "special error" in the above syntax is used
to indicate that something has gone wrong, without giving any indication of the cause; the
statement
ERROR:
generates a system-defined error. It is provided
to cover those "impossible" cases which should never
occur in correct programs but which it is always best to check for (such as
falling out of a loop that should never terminate normally, or
arriving at the ENDCASE
of a SELECT statement that claims to handle
all the cases). It can only be caught using the ANY option in a catch phrase
(sec. 8.2.3). It is customarily handled by the debugger.
8.1.1 ERROR in expressions
When an ERROR is declared to return values, this is purely for
syntactic convenience, since one of the principal features of an
ERROR is
that it does not "return". The reason for doing this it to allow the
ERROR to
stand in an expression context considered invalid or impossible. Such
declarations of returned values are not necessary; if an
expression has an ERROR
type (or SIGNAL type raised as an error) and returns
no value, then that expression can be used wherever an expression of any type
is required. For example:
Color: TYPE = {red
orange, yellow, green, blue,
violet}: c: Color,
button: [0..2);
button 4- SELECT C FROM
red => 0,
yellow => 1, blue => 2,
ENDCASE
=> ERROR;
In the example, the only valid colors for buttons are red yellow, and blue. Any other value results in an
error (in this case, the unnamed system error). Such constructs allow an
inexpensive way to get to the debugger in those "impossible"
cases that arise from program errors.
A fine point:
If the
ERROR type is defined to return a value. any use of that expression must be
type correct with respect to the "returned" value.
8.2. Control
of generated signals
Any program which needs to handle signals must anticipate
that need by providing catch phrases for the various signals that
might be generated. During execution, certain of these catch phrases will be enabled at different times to
handle signals. Loosely speaking, when a signal S is generated, the
procedures in the call hierarchy at that time lk ill be given a chance to catch the
signal, in a last-infirst-out order. Each such procedure P, if it has an enabled catch
phrase, is given the signal S in turn. until one of them
stops the signal from propagating any further (by mechanisms which are explained
below). 1' may
decide to reject S (in
which case the next procedure in the call hierarchy will
be considered), or P may
decide to handle S by taking control and attempting to recover from the signal.
8.2.1. Preparing to catch signals: catch phrases
A catch phrase has the following form:
CatchTail = Catch I
ANY => Statement
Catch =
ExpressionList => Statement
CatchSeries = CatchTail
Catch CatchSeries
The expressions in the ExpressionList (semantically
restricted to a list of variables) must evaluate to the names of
signals (unless otherwise stated, we use signal to stand for both ERROR and SIGNAL). The
special identifier ANY
will match any signal (sec. 8.2.3). Note that if ANY occurs, it must be
last.
A catch phrase is written as part of an argument list,
just after the last argument and before the right bracket.
Catch phrases may appear in a procedure call, SignalCall, NEW, START, RESTART, STOP, JOIN, FORK. or WAIT (but not in a RESUME or RETURN). A
catch phrase may also be appended to the BEGIN of a block or the DO of a loop statement
by means of an EnableClause. The applicable syntax
for a call and for a block or loop statement is
Call =
Variable ComponentList CatchSeries I
Variable CatchSeries
Block =
BEGIN --
(from Section 4.4)
OpenClause
EnableClause
DeclarationSeries
StatementSeries
Exits
Clause
END
EnableClause = empty I
ENABLE Catchltem
:
ENABLE BEGIN CatchSeries
END ; ENABLE BEGIN CatchSeries
END ;
Note
that the EnableClause is always followed by a semi-colon, and BEGIN...END must
be used if there is more than one Catch in an EnableClause.
The main difference between the two kinds of catch phrases
(ENABLE and
!) is the scope of their influence. A catch phrase on a Call is only
enabled during that call. A catch phrase at the beginning of a
compound or loop statement is enabled as long as control is in that block; it
can catch a signal resulting from any call in the block (or
generated in the block).
To
clarify the scope of influence of ENABLE clauses, the following two
diagrams are reproduced from chapter 4. The scope of each
phrase extends over others with greater indentation.
BEGIN
OpenClause
EnableClause
DeclarationSeries StatementSeries ExitsClause
END
LoopControl
DO
OpenClause
EnableClause
StatementSeries LoopExitsClause
ENDLOOP
Note
that catch phrases enabled in the EnableClause of a Block or LoopStmt are not
in force in the ExitsClause or LoopExitsClause.
Fine
point:
Procedures declared in the
DeclarationSeries (of any enclosed Block) do not inherit the catch phrases in
the EnableClause (this is not shown by the diagrams).
8.2.2. The
scope of variables in catch phrases
Catch phrases are called to handle signals (the exact
mechanisms are discussed in the next section). The naming
environment that exists when a catch phrase is called (in order of innermost to
outermost scope) includes any parameters passed with that
signal (these are declared as part of a signal's definition), and
any variables to which the procedure or program activation containing the catch phrase has access.
If a Catch has more than one label (or the label ANY), where the types of those labels are not identical. then the signal's arguments are not
accessible in the Statement chosen by that Catch.
If. however. there is exactly one type for the signals named
in a Catch's ExpressionList, then the signal's arguments
are accessible in the statement following "=>". The names used are
the parameters given in the signal's declaration, just as for
procedures. For example, a catch phrase for signal BlockTooLarge (defined earlier)
might be used in a section of code such as:
-- in StorageDefs
BlockTooLarge: SIGNAL [z: Zone. needed: CARDINAL] RETURNS[newStorage: DESCRIPTOR FOR ARRAY OF CARDINAL]:
GetiiloreS forage: PROCEDURE [z: Zone, n: CARDINAL]
RETURNS
[DESCRIPTOR FOR ARRAY OF CARDINAL]:
-- in a user program
p: POINTER TO Account:
p 4- Allocate[sizE[Account] !
BlockTooLarge =>
REsumE[GetAloreStoragetz needed]:
The
names z and
needed in
the catch phrase refer to the parameters passed along with the signal from
Allocate (see
sec. 8.2.5 for a discussion of RESUME).
8.2.3. Catching signals
When a signal is generated, what really happens is that
the signal code, and a descriptor for the actual arguments of the
signal, are passed to a Mesa run-time procedure named Signaller. .S'ignaller's definition
is
Signaller. PROCEDURE[S: SignalCode. in: Message]:
Here s identifies
the signal being generated.
and in contains
its arguments.
(Actually, different procedures are used to distinguish between SIGNAL, ERROR, and
RETURN WITH ERROR.)
Signaller proceeds
to pass the signal and its argument record from one enabled catch phrase to the
next in an orderly fashion. The order, at the procedure
level. follows the current call hierarchy, from the most
recently called procedure to least recently called, beginning with the procedure that generated the signal itself If
the caller of a procedure is the outermost block of code for a program, the
Signaller will
follow its return link to
continue propagating the signal (the return link points to the
frame that last STARTed
the module (sec. 7.8)).
If, in place of SIGNAL or ERROR, a RETURN WITH ERROR is
used, the procedure that generated the error is first deleted (after releasing
the monitor lock, if it is an ENTRY procedure), and propagation of the error begins with its caller.
As Signaller
considers each frame, it looks to see whether that frame
has any enabled catch phrases: if so, Signaller calls the innermost catch
phrase as if it were a procedure, passing it the SignalCode and Message. The innermost catch phrase
is defined to be
either the one after "1" attached to
the currently incomplete procedure call for that frame, or the
one following an ENABLE in the innermost enclosing
block that contains that call.
Because signals can be propagated right through the call
hierarchy, the programmer must consider catching not only signals
generated directly within
any procedure that is called, but also any generated indirectly as a result of
calling that procedure. Indirect signals are those generated by procedures
called from within a procedure that you call, unless they are stopped before
reaching
you.
When a catch phrase is called. it behaves like a SELECT statement:
it compares the signal
code passed to it with each signal value in the ExpressionList of each Catch in
the catch phrase. If the signal code matches one of the signal values,
control enters the statement following the "=>" for that
Catch; if not, the next Catch is tried. A Catch consisting
of "ANY =>
Statement" automatically matches any signal code (and is
the only way to catch the unnamed ERROR generated by
the standalone ERROR statement
discussed in section 8.1).
Fine
point:
The ANY catchall is
intended primarily for use by the debugger. and should generally
be avoided. It matches any
signat. including UNWIND and all system-defined signals that
might indicate some catastrophic condition (a double memory parity error, for example).
When a match is found, that Catch is said to have caught or accepted the signal. If no
alternative in a catch phrase accepts the signal, there may be
another enabled catch phrase in some surrounding block. If so, the first catch
phrase sends control to the second one so that it can inspect the signal, and
so on until the last enabled catch phrase in that routine has had a chance at
the signal. If no
catch phrase in the routine accepts the signal. control
returns to Signaller with
a value indicating that the signal was rejected. and Signaller propagates the
signal to the next level in the call hierarchy. In fact_
all catch phrases are called by Signaller
as if they were procedures of the following type:
CatchPlimse: PROCEDURE[s: SignalCode, es.s-age]
RETURNS[{Reject, Unwind. Resume});
The
SELECT-like statement
associated with each Catch has
an implicit Reject return
as its ENDCASE: hence,
if control simply falls out of the statement, the signal is rejected.
Fine
point:
If the same signal. foo, is enabled in several nested catch phrases in a procedure. each is gi\
en a chance to handle foo if the inner ones reject the signal.
Signaller continues
propagating the signal up the call chain until it is exhausted. i.e., until the
root of the process has considered and rejected the signal. At
that point, an uncaught signal has
been generated, and drastic action must be taken.
Mesa guarantees that all signals
will ultimately be caught and reported by the Debugger to the user. This is
helpful in debugging because all the control context which existed when the
signal was generated is still around and can be inspected to investigate
the problem.
The declaration of Catch Phrase above indicates
three reasons for returning to Signaller.
The first, Reject, has already been
discussed. The
third, Resume, is discussed in section
8.2.5.
The second reason, Unwind, is used when a catch phrase has accepted a signal
and is about to do some form of unconditional jump into the body of
the routine containing it (this is the only form of "non-local goto"
in Mesa). The jump may be generated by a Go-ro statement (sec. 4.4), an EXIT or
LOOP (sec.
4.5), or a RETRY or
CONTINUE (see
below). aslmmediately preceding such a jump. the catch phrase
returns to Signaller with
result Unwind: it
also indicates the frame containing the catch phrase and the
location for the jump. This causes Signaller
to perform the following sequence of actions:
(1) Beginning
at the frame in which the original signal was generated (or its caller, if a RETURN WITH ERROR was
executed), it passes
the signal UNWIND to each
frame. This signal tells that activation that it is about to be
destroyed and gives it a chance to clean up before dying.
Signaller then
deallocates the frame and follows the same path as it did for the original
signal to continue unwinding control. When it comes to the frame containing the
catch phrase, it stops.
(2) Signaller then arranges for the jump
to take place, and simply does a return to that frame, destroying
itself in the process.
Every Mesa program contains the pre-declared value
UNWIND:
ERROR = CODE:
Fine
points:
One cannot say RETURN
in a catch phrase to return from the enclosing procedure. This is an
implementation restriction
that may be removed in the future, caused by the way in which a catch phrase is
"called" like a procedure
itself.
The UNWIND sequence gives each activation that
is to lose control a chance to make consistent any data structures for which it
is responsible. There are no constraints on the kinds of statements that it can
use to do this: procedure
calls, loops, or whatever are all legal. If, however, a catch for
the UNWIND signal, such as,
START Nextlairase[!
UNWIND
=> GOTO BailOur]:
decides itself to perform a control transfer that would also initiate an
UNWIND, this will override the original UNWIND. and Signaller will stop right there, as if the second UNWIND catch had been the originator
of the UNWIND.
2.4. RETRY and CONTINUE in catch phrases
Besides GOTO. EXIT, and LOOP. there are two other statements. RETRY and
CONTINUE, which
initiate an UNWIND. These can be used within catch
phrases.
RETRY means
"go back to the beginning of
the statement to which this catch phrase belongs": CONTINUE means
"go to the statement following
the one to which this catch phrase belongs" (what is called
Next-Statement in
chapter 4).
For
a catch phrase in a Call, the catch phrase "belongs" to the statement
containing that Call. Thus.
if the signal NoAnswer is
generated for the call below, the assignment statement is retried:
answer 4- GetReply[Send["What next?"] NoAnswer => RETRY]:
On the other hand, if CONTINUE had been used instead, the
statement after the assienment would be executed next (and the
assignment would not be
performed). For example, suppose the procedure ReadLine reads characters from a file
up to a carriage return and appends them onto the string buffer. If reading beyond the end
of file raises the signal StreamError,
the call
ReadLine[l StreamError => IF buffer.length> 0
THEN
CONTINUE];
deals
with the case of no carriage return after that last line in the file. If there
is no such final line, other thatch phrases higher on the call chain
are given a chance to catch the signal.
For a catch phrase after ENABLE, there are two cases to
consider, blocks and loops. In a block, the catch phrase "belongs" to
that statement; the next section shows an example. In a loop, the catch phrase
"belongs" to the body of
the loop, and CONTINUE
really means "go around the loop again." The
following two examples are equivalent:
UNTIL p= NIL
DO
ENABLE TryList2 => BEGIN p4-1is12; CONTINUE END:
ENDLOOP:
UNTIL p= NIL
DO
BEGIN
ENABLE TtyList2 => BEGIN p4-list2; CONTINUE: END:
END:
ENDLOOP;
In any case, recall that an Unwind is initiated prior to
completion of a RETRY or CONTINUE.
If
a procedure call in the Initialization clause of a declaration contains
a catch phrase, this catch phrase cannot contain RETRY or
CONTINUE since
it is in no well defined' statement.
8.2.5. Resuming from a catch phrase: RESUME
The third alternative available to a catch phrase. after Reject and Unwind. is Resume. This option is invoked
by using the RESUME statement
to return values (or perhaps just control) from a catch phrase
to the routine which generated the signal. To that routine, it appears as if
the signal call were a procedure call that returns some results.
The syntax for RESUME is
just like that for RETURN:
Statement = ResumeStmt I
RETRY
I CONTINUE I ...
ResumeStmt =
RESUME
I
RESUME
[ ComponentList
When Signaller
receives a Resume
from a catch phrase, it simply returns and passes the accompanying
results to the routine that originally called it (i.e.. that generated the
signal). If the signal
was generated by an ErrorCall and
a catch phrase requests a Resume,
Signaller simply generates a signal itself
(which results in a recursive call on Signaller); its declaration is
Resumer/Tor. PUBLIC ERROR;
Since it is an ERROR, one cannot legally
RESUME it.
The
ability to RESUME and
return values gives
the ability to deal with exceptional conditions in a way
that is quite inexpensive in the non-exceptional case. For example. consider
the declaration
StringBotindsFault:
SIGNAL
[s: STRING] RETURNS [ns: STRING];
This
signal allows the user to deal with the situation where characters are to be
added to a string that is already
"full". Thus
the call
AppendChar[str,
c ! S
tringBoundsFault =>
BEGIN
us 4- AllocateString[s.maxlength+
10]; AppendString [ns, s];
FreeString
[s];
RESUME[sfr
4- us]: END);
allocates a larger string and updates the local variable
whenever the string is about to overflow. Of course, the
procedure AppendChar has
to be written in such a way as to deal with the signal being resumed
with a new string value. This application of signals can cause errors if there
are any procedures between the signaller and the catcher that
have their own idea about the location of the
string. One possible fix (if such situations are possible) is to have a
second signal
Stringilloved:
SIGNAL
[old, new: STRING] = CODE;
that
is raised by AppendChar after
StringBoundsFault is
resumed.
The presence or absence of the ComponentList depends on whether the
signal caught is declared to return values. In a Catch whose ExpressionList contains more than one
signal, one can RESUME
only if all signals have equivalent types. For example:
ASig: TYPE = SIGNAL
RETURNS [CARDINAL];
sigl: ASig:
sig2:
ASig;
sig3:
SIGNAL
RETURNS [CARDINAL]; sig4: SIGNAL;
ENABLE
BEGIN
sigl, sig2 => RESumE[3]: --
legal
sigl, sig3 => REsumE[0]; -- legal
sigl, sig4
=> RESUME[1]: --
illegal
END;
8.3. Signals within signals *
What happens if, in the course of handling a signal, firstSignal, a catch phrase (or
some procedure called by it) generates another signal. secondSignal? Handling nested
signal generation is almost exactly like non-nested
signal propagation. Generating the signal will call Signaller (recursively, since
the instance of Signaller responsible
for the first signal is still around), and it propagates the
new signal back through the call hierarchy by calling a
second activation of Signaller. say
"Signaller?'. When
in the course of doing this it encounters the previous activation of
Signaller ("Signalled"), then
something different must be done.
If firs/Signal
is not the same as secondSignal. Signaller2 propagates it right through Signalled. and all
the activations beyond it arc also given a chance to catch secondSignal.
On the other hand, if secondSignal = firstSignal. then all of the routines
whose frames lie beyond Signalled,
up to the frame containing the catch phrase called by Signallerl, have already had a
chance to handle firstSignal, so
they are not given it again. In order to skip around that section of the
call hierarchy. Signaller2 simply
copies the appropriate state variables from Signallerl. Next. Signaller2 skips over the frame containing the catch phrase
(by following its return link), and continues propagating secondSignal normally.
For the programmer, the main import of nested signals is
that one needs to consider, when writing a routine, not only
what signals can be generated. directly or indirectly, by the called
procedures, but also those which can be generated by catch
phrases in that procedure or even the catch phrases of any
calling procedures, also both directly or indirectly.
CHAPTER 9.
PORTS AND CONTROL STRUCTURES *
Mesa has, in addition to procedures. another mechanism by
which programs may transfer control. This mechanism is called a PORT: PORTS allow
separate modules or procedures to act as coroutines. When one calls a procedure and it returns, the
procedure is finished: if the same operation is needed again.
another call will create a new activation of it to perform that action.
However, when a coroutine returns control, it does not finish and disappear. Calling
it again only resumes it from where it left off. The advantage of a this scheme
is that the coroutine may keep some of its state from call to call
encoded in its program counter: i.e., if it is at a certain place in its code,
then that place does not need to be encoded somehow and saved as a
variable in order to decide how to proceed when next called.
Actually, as described later, PORTS are
normally used in pairs, just like electrical plugs and sockets. one
for each side of the connection. If two coroutines A and
B are
connected, what is seen by A as a call to B appears to B as a return from A, and
vice-versa. Thus, both A and B regard
the other as a facility to be called to accomplish some processing task. For
instance, if ReadFile is
a coroutine for reading characters from a file which are then given,
one at a time, to another coroutine, its view is that it reads characters from
the file and calls the other coroutine to process them (in some unspecified
way). WriteFile, on
the other hand, a coroutine for writing characters into a file, would call
a coroutine to get the next character to be written. Together these two
coroutines could make a file copying program.
A coroutine needs to be able to send arguments and to
receive results. The language facilities for doing this closely
mirror procedure parameter and result lists. For example, a PORT over which ReadFile could send a character would
be declared by ReadFile as
Out: PORT[Ch:
CHARACTER]:
The
port over which WriteFile receives
a character, and which could be connected to ReadFile's Out PORT, is declared as
In: PORT
RETURNS[CHARACTER]:
There is only one other consequential difference between
procedures and coroutines. A procedure can be called at any time
because a new activation is created. which will always consume the arguments
sent to it as soon as it begins. However, if two coroutines like ReadFile and WriteFile communicate, in order for
the transfer of control and arguments to go smoothly, WriteFile must be prepared
to receive a character when ReadFile
sends it. Coroutines are not parallel processes, and one
has to be started before the other, so it is guaranteed that the first attempt at transferring control between
ReadFile and
WriteFile will
not work smoothly. Fortunately, Mesa provides a mechanism for
starting a whole set of interconnected coroutines to get them past this
start-up transient (sec. 9.2). The most important property
of the mechanism is that the coroutines themselves need never be concerned
about the startup transient -- they are written as if it never happens.
9.1. Syntax
and an example of PORTS
The syntax for declaring a port is the
following:
PortTC _
-
PORT ParameterList ReturnsClause
RESPONDING PORT ParameterList ReturnsClause
The ParameterList
and ReturnsClause may
both be empty, just as for procedures. RESPONDING PORTS arc covered in section 9.3.
The syntax for making a call on a port is exactly the same
as for calls on procedures (both
as statements and functions).
The following pair of program modules
implement the coroutines ReadFile and
WriteFile described
earlier: they
use the ports Out and In, respectively:
DIRECTORY
FileDefs: FROM "filedefs" USING [
NUL, FileHandle, FileAccess, Open File. ReadChar,
EndOfFile, CloseFile];
ReadFile: PROGRAM[name: STRING] IMPORTS FileDefs = BEGIN
OPEN FileDefs;
Out: PORT[ch: CHARACTER];
input:
FileHandle;
input
4- OpenFile[name: name, access: FileAccess[ Read]];
STOP;
UNTIL EndOfFile[input]
DO
Ou4ReadCharfinput]]; -- PORT call:
send a character from the file
ENDLOOP;
CloseFile[input];
Out[NUL]; --
send a null character to indicate end-of-file
END.
DIRECTORY
FileDefs: FROM "filedefs" USING [
NUL, FileHandle, FileAccess,
OpenFila WriteChar, CloseFile]:
WriteFile: PROGRAM[name: STRING] IMPORTS FileDefs = BEGIN
OPEN FileDefs:
In: PORT RETURNS[ch: CHARACTER]:
char: CHARACTER;
output:
FileHandle:
output
4- OpenFile[name: name, access: FiieAccess[New]];
STOP;
DO -- until
In sends
a NUL
char 4-
1,10; -- PORT call: get a character
IF char =
NUL THEN EXIT; --
check for end of stream
WriteChadoutput, char]; -- write the character into the file
ENDLOOP;
CloseFile[output];
END.
ReadFile first
initializes its variables and opens the input file (with Read access). When it is restarted,
it loops, reading characters from the file and sending them over its Out PORT until it reaches the end of the input
file: then it sends a single NUL character. If it regains control, it simply returns.
WriteFile. after
creating and opening a new output file. loops, reading characters from the port
In and
writing them to the output. If it receives a NUL character, it closes the
output file and returns. Thus, if ReadFile and WriteFile's
ports were connected
so that they were working together as coroutines.
ReadFile would
never regain-
control after sending the NUI. character.
9.2. Creating and starting
coroutines
To set up the above two programs as coroutines. their
respective ports must be connected. and then they must be
started individually, with the start-up transient handled. This is usually done
by another. controlling program like the following:
|
DIRECTORY
TrapDefs: IODefs: ReadFile: WriteFile:
|
FROM
"trapdefs" USING [Port Fault],
FROM "iodefs" USING [ReadLine,
WriteS tring],
FROM
"readfile". FROM "writefile";
|
CopyMaker: PROGRAM IMPORTS IODefs, reader: ReadFile, writer: WriteFile
BEGIN OPEN IODefs;
input: STRING 4- [256];
output: STRING 4- [256];
--
first ask the user for the names of the input and output files
WriteString["Name of
input file: "]; ReadLine[input];
WriteStrine Name of output
file: "1; ReadLine[output];
-- create and initialize instances of ReadFile and WriteFile;
START reader[inpul;
START writerfoutput];
--
connect their ports and then restart them to get them synchronized
CONNECT writer. In TO reader.Out: CONNECT reader.Out
TO writer1n;
RESTART writer{ TrapDefs.PortFault => CONTINUE];
RESTART reader{ TrapDefs.PortFault => ERROR];
END.
Logically. Copyillaker
is a very simple program. However, it must know how to
start ReadFile and
WriteFile and
how to connect their ports (and it must
handle the signal PortFault -- see below). This is typical of the use
of PORTS: the
coroutines themselves do not know (nor should they care) exactly
which other program(s) they are connected to; each PORT is
viewed as a virtual facility to be called to perform some task.
such as providing the next input or taking an output.
Copyil faker first
requests the names for the input file to be copied and the output file to which
it should be copied. The names are read into the string
variables input and
output. Then
an instance of ReadFile is
made and initialized.
Similarly. an instance of WriteFile is created and STARTed. When
the NEWS are
performed. pointers to the instances are stored (into reader and writer above).
After both instances have been created and initialized,
CopyAlaker performs the operations to get them past the startup transient.
First it connects writerin (i.e.,
WriteFile's In PORT)
to reader.Out:
this simply amounts to storing a pointer in writerin to the PORT reader.Out. Then it connects readerOut to writerIn.
Fine
point:
The STARTs must be
performed before the ports are connected. In general, it is not legal to access
a module's variables before it has been started (and the variables have been
initialized). Calls to procedures are allowed. however: they are handled by the start trap
mechanism (sec. 7.8.3).
Once the CONNECTS are done, all that remains is to get the two
coroutines synchronized. First. Writei'lle
is RESTARTed: it makes a port call on In to get the first character
to be written into the file.
The port call almost works because In is connected to another
port. But. since ReadFile is
not waiting for control to return over its Out port, it doesn't quite work.
This fact is detected because a part of the underlying representation of Out indicates that no instance
is pending on
it (i.e., waiting to receive control via Out). This results in a trap, which is quickly converted
into the ERROR PortFault. CopyMaker clearly
anticipated this as part of the normal startup transient (as evidenced by
the presence of the catch phrase on the START statement). The CONTINUE in
that catch phrase means: "forget about this signal and
continue execution at the next statement in CopyMaker."
The next action taken by CopyMaker is co RESTART ReadFile.
ReadFile reads the first character from
the input file and attempts a port call on Out, passing the character as its argument. This is the
end of startup transients: this port call works. It
works because WriteFile was
left pending on In when
it attempted to call it, even though that call did not go through completely.
Since WriteFile is
pending on In,
it resumes, stores the argument in char, and proceeds. From now on,
port calls between ReadFile
and WriteFile
will go smoothly, with no further intervention by CopyMaker. (Moreover, a port
call is more efficient than a procedure call because no frames are allocated
and deallocated in the process).
When there are no more characters in the input file, ReadFile sends a final NUL character
which causes WriteFile to
close the output file and to return. This returns control to CopyMaker, who, in this
example, also returns.
The
above description skipped one or two important details of the startup process
and port calls. The next section corrects those omissions and
discusses the underlying representation of ports.
9.2.1. The
CONNECT
statement
The first CONNECT statement
in CopyMaker is equivalent
to the following (illegal) assignment: writer.ln.link 4- readerOut:
This assignment is illegal because, at the language
level, a PORT does
not look like a record with a link component.
Nevertheless, the code produced by the compiler for the CONNECT statement
in CopyMaker performs
exactly this assignment (the compiler is allowed to treat PORTS in
terms of their underlying representations, without regard to type
- it implements type checking). Note that CONNECT is not a symmetric operation: it
only connects in one direction.
The syntax for CONNECT is the following:
ConnectStmt = CONNECT expression TO expression
These expressions must both be valid IeftSides. The
first expression must conform to some PORT type, and the second may conform to either a PORT or
a PROCEDURE type
(see sec. 9.2.2 for a discussion of ports connected to procedures).
The types of the two expressions must be port-compatible. To be port-compatible,
the result list of one must be compatible (see definition in sec.
5.2) with the parameter list of the other, and vice versa. This basically says
that the first port sends what the second expects to receive, and the second
sends what the first expects
to receive.
Fine
point:
In the
present compiler. the CONNECT statement is not implemented
9.2.2. Low-level actions during a PORT call
A
PORT is
represented as a record with two components. one of which is a pointer to
another PORT, and
one of which points to a frame (the frame which is pending on that PORT). Its
definition is:
Port: TYPE = MACHINE
DEPENDENT RECORD
frame: POINTER TO Frame, -- internal view of a frame link: SELECT OVERLAID * FROM
null =>
[value: NullControlLink],
port =>[portDesc:
POINTER TO Port],
procedure =>[procDesc: ProcedureDescriptor],
ENDCASE
]:
We will not discuss the internal format of the types Frame, ProcedureDescriptor, or
NullControlLink here.
The first two are the underlying representations for a frame and a procedure
value, respectively. The last is just a special value which is used to initiate
a trap if the port is used without having been connected first.
The variant part of a Port distinguishes three cases (how these cases are
identified is a function of the underlying implementation).
The null case
is how a Port which
has not been connected is represented; it is what causes a trap if a call
on the port is made before it is connected (this is called a linkage fault). If the Port is connected to another Port (the normal case), then the port variant holds.
Procedure calls, port calls, and returns are all
examples of control transfers: each
suspends the execution of one activation and transfers control
to another. They also perform other actions, such as creating or destroying
frames, etc. Every control transfer from one activation to another has a source
control link and
a destination control link. By control
link we mean a procedure value, a pointer to a port, or a pointer to a frame.
All the high level control transfers in Mesa are
built from one common, low-level mechanism called XFER, which
effects the transfer from a source to a destination. In fact, it is possible to
bind any form of control link to any other; thus, if the program
uses a port, it could be bound to a procedure, and calls on the
port would actually result in calls on the procedure. A RETURN from
the procedure would cause control to come back in through the
port. Similarly, a procedure value could contain a pointer to a port,
in which case calls on that "procedure" would actually result in a
port transfer via the destination port to the coroutine pending on it.
The common part of a Port record is used when control is returning over a PORT. When
a coroutine does a port call and is suspended, a pointer to its frame is
assigned to the frame component
of that port. Then, when control returns over that port (usually
because of a port call on the port to which it is connected),
the frame field
is used to locate the instance which is to be resumed.
The value contained in the frame component may indicate that
it is null. If
so, a control fault trap
will be generated should a transfer using that port ever
occur. This condition can arise for two different reasons:
(1) Due
to startup transients, the instance which would normally be pending on that
port is not.
(2) There
is a genuine error in the way that a configuration of coroutines has been
constructed, and control is attempting to "loop back" into a
coroutine. The simplest example of this situation is the following: consider a
coroutine A with
two ports, p1 and
p2. If
pl were
connected to p2, then
a port call on pl would
clearly result in a control fault when p2 was reached in the call, since A cannot be pending on both pl and p2 simultaneously.
"Ilie action
taken on a control fault during, a port call is
described in the next section.
There is one last important detail about a port call: as
part of the action of returning to a port. its link is set to point at the
source port if the return is actually part of a port call. This constitutes an indirect return link. However.
if the return is from a procedure to which the port is bound, then the link field is not changed. This
is so that the procedure value in the port is not destroyed: thus. future
calls on that port will always result in new activations of that procedure.
Storing an indirect return link in the link field of a destination port
means that the next port call on it will cause control to
return via the port from which control most recently arrived. Using this, one can
write coroutines that may be invoked by more than one coroutine connected to a
given port: control will always return to the last coroutine which
sent control over that port. For instance, the coroutine WriteFile above could be
given its input stream of characters from many sources. If the system
procedures ReadLine and
PliriteString both
had ports connected to the port In in
an instance of WriteFile, then
everything typed to the user and typed by him would be recorded in a typescript
of his
interactions with the system.
9.2.3.
Control faults and linkage faults
When a control or a linkage fault occurs, Mesa changes the
trap into the ERROR PortFault or LinkageFault, respectively.
These signals are part of a Mesa system interface TrapDefs and should be
imported from there by any program, such as CopyAfaker, which configures coroutines. In TrapDefs they are defined as follows:
PortFault, LinkageFault: ERROR:
Generally, programs should not handle the LinkageFault signal: ports
should be properly connected before they are used. We
include it here only for completeness (the fine point at the end of this section
discusses LinkageFaults further).
These signals, unlike most other signals, are not passed
initially to the instance which caused the fault (call it the
culprit), but
rather are given first to its owner:
the frame to which the culprit's return
link points. This is so that the owner may catch the signal and cause an UNWIND without
the culprit's frame being destroyed as it would normally be. In the previous
example, CopyAlaker is
the owner and ReadFile
and WriteFile
are possible culprits.
Note: if the owner does not catch
the PortFault or
the LinkageFault signal,
it may possibly be unwound itself This
would leave the culprit's return link pointing to an invalid address, because
the owner's frame would have been
freed.
The standard action taken by the owner when receiving a PortFault while starting a
coroutine is to press on and start the other members of the
configuration. CopyAfaker follows
this pattern: when it starts the instance of WriteFile and a control
fault is generated, it simply exits the catch phrase for PortFault and starts the
instance of ReadFile. This is the
recommended way to start configurations of coroutines.
Fine
point:
If the source port in a port call is unbound (i.e.. not
connected), a LinkageFault ERROR is generated. This cannot be handled in the same manner as a control fault. If the
catcher of this signal causes an UNWIND. there will be no way to restart the
activation which caused the linkage fault: it will be pending on a port, and RESTARTing it will cause an error.
This difficulty makes starting coroutines before connecting their ports an ill-advised thing to do. It
is much better to do the CONNECTs first, and then stan each activation.
9.2.4. Saving arguments during
faults
When a port call faults, the instance which attempted the
call is left pending on the source port before the trap is changed
into the PortFault or
LinkageFault signal.
This is done by a Mesa procedure called the FaultHandler, which is called in
response to the trap. In the case of starting writer above, this procedure did the following:
(1) It
set the instance of WriteFile to
be pending on its In port
(the trap process provides information about which instance caused the trap.
and what the source port was):
(2) By
some low-level control mechanisms. it invoked the Signaller (sec. 8.2) as if from the owner
of writer and
simultaneously did a RETURN.
Thus, that activation of FaultHandler disappeared and the Signaller was invoked as a single
action.
Later,
when reader called
Out. control
returned to writer via
In, which
continued normally because it was pending on In. To writer it appeared as if the first
port call worked correctly.
Reader's call
on Out passed
an argument along with control. If Copytilaker
had started reader
first, what would have happened to
that argument? Given the above
description of FaultHandler, the argument would have been
lost: there were no provisions for buffering or saving
arguments.
To
handle this, the FaultHandler buffers
any arguments passed over a port on which a fault occurs. Instead
of performing action (2) above, it actually does the following:
(2') It buffers the arguments for the port call, makes it
appear that it (the FaultHandler itself)
is pending on the source port, then calls Signaller, but without
destroying itself in doing so.
For
the following discussion, assume that the startup sequence in Copy]%faker had been written as
follows (the order of starting reader and writer has been inverted):
-- connect their ports and then restart them to get them
synchronized
CONNECT reader.Out TO writer.ln; CONNECT writer.ln
TO reader.Out;
RESTART readerf! TrapDefs.PorzFault => CONTINUE];
RESTART write?' ! TrapDefs.PortFault => ERROR];
END.
The
revised version of FaultHandler would
then do the following when writer was
RESTARTed and
tried its first call on In:
The instance of FaultHandler which had left itself pending on Out would have been resumed
instead of reader. FaultHandler would
then have set reader.Out.frame so
that reader was
again pending on it. Finally, it would have transferred control back through writer.ln along with the
arguments it had saved from the original call, destroying itself in the
process.
The only remaining question is: "How does the FaultHandler know whether or not
arguments should be buffered?" This question is not trivial:
for example, if every instance of FaultHandler
buffered arguments for every trapped port call, including
those for ports like In, extra
"ghost" port calls would occur during startup. FaultHandler determines whether
or not to save arguments by inspecting information left
by the compiler in the object code of every port call. This decision is made
by the compiler on the following basis:
Arguments should only be
buffered for a port which is not a
RESPONDING
PORT and which
does have a non-empty ParameterList.
The next section discusses RESPONDING PORTS.
9.3. RESPONDING PORTS *
The normal analogy between a port and a procedure
in terms of passing arguments and receiving results breaks
down in one case. If a port is used both for sending arguments and for receiving
results, it might do so for either of the following t o reasons:
It
sends arguments to be processed. and the returned results of the port call
indicate how they were handled (this closely mirrors
procedures).
It
receives data to be processed. and, having done so responds by sending results
of the processing back over the same port (there is no
procedure analog of this).
The second case can not be distinguished from the
first by usage in a program because the actions of sending
and receiving over a port are intrinsically intertwined with the notation for a
Call. Thus.
it would not be
possible to determine whether BothWays
was a normal or a responding port by looking
at the following (partial)
module:
. . .
Both Ways: PORT[s: STRING] RETURNS[t: STRING];
aString:
STRING; bString: STRING;
aString BothWays[bString];
To resolve this difficulty, the programmer may
declare a port to be RESPONDING. For example, InOut: RESPONDING PORT[response: {okay. error}] RETURNS[inpul:
STRING];
The module using InOut responds with either okay or notOkay to each string it has
received.
If InOut faults
the first time it is used, the Fauldlandler
will not buffer the response value for that call. Since InOut must, for type conformance,
be connected to a port such as
Outln: PORT[oulpul: STRING]
RETURNS[response: {okay. error}],
both initial argument lists (the response for the first call on InOut, and the output of the first call on OutIn) cannot be buffered. The
keyword RESPONDING indicates
which initial argument list should be discarded (InOut's initial response, in this case). For similar
reasons, a responding port may not be connected to a procedure.
and two responding ports may not be connected together.
Fine
point:
In the current
compiler. RESPONDING PORTs are not implemented
CHAPTER 1 O.
PROCESSES AND CONCURRENCY
Mesa provides language support for concurrent execution of
multiple processes. This allows programs that are
inherently parallel in nature to be clearly expressed. The language also
provides facilities for synchronizing such processes by means of
entry to monitors and waiting on condition variables.
The next section discusses the forking and joining of
concurrent process. Later sections deal with monitors, how their
locks are specified, and how they are entered and exited. Condition variables are
discussed, along with their associated operations.
10.1. Concurrent execution, FORK and
JOIN.
The FORK and JOIN statements allow parallel execution of two
procedures. Their use also requires the new data type PROCESS. Since
the Mesa process facilities provide considerable flexibility, it is easiest to understand them by first looking at a
simple example.
10.1.1. A process example
|
Consider an application with a front-end routine providing input lines:
ReadLine:
PROCEDURE
[Y. STRING] RETURNS [CARDINAL] = BEGIN
C: CHARACTER;
s.length 4- 0;
DO
c ReadCharn:
IF ControlCharacter[c] THEN DoAction[c] ELSE AppendChar[s,c];
IF c = CR THEN RETURN [s.length]; ENDLOOP;
END;
The call
|
interactive composition and editing of
|
n <- ReadLine[buffer]:
will collect a line of user type-in up to a CR and put it in some string
named buffer. Of
course, the caller cannot get anything else accomplished during the
type-in of the line. If there is anything else that needs doing.
it can be done concurrently with the type-in by forking to ReadLine instead of calling
it:
p n- FORK ReadLine[bufferl:
• • •
<concurrent computation>
. . .
4- JOIN p:
This allows the statements labeled <concurrent
computation> to proceed in parallel with user typing (clearly,
the concurrent computation should not reference the string buffer). The FORK construct
spawns a new process whose result type matches that of ReadLine. (ReadLine is
referred to as the "root procedtire" of the new process.)
p: PROCESS RETURNS
[CARDINAL]:
Later, the results are retrieved by the JOIN statement,
which also deletes the spawned process. Obviously, this must not
occur until both processes are ready (i.e. have reached the JOIN and
the RETURN, respectively);
this rendevous is synchronized automatically by the process facility..
Note
that the types of the arguments and results of ReadLine are always checked at
compile time, whether it is called or forked.
The
one major difference between calling a procedure and forking to it is in the
handling of signals; see section 10.5.1 for details.
10.1.2. Process language constructs
The declaration of a PROCESS is
similar to the declaration of a PROCEDURE, except that only the return record is specified. The syntax is formally specified as follows:
TypeConstructor = I ProcessTC
ProcessTC = PROCESS ReturnsClause
Retu rnsClause =
empty I RETURNS ResultList -- from sec. 5.1.
ResultList =
FieldList --
from sec. 5.1.
Suppose
that f is
a procedure and p a
process. In order to fork f and
assign the resulting process to p, the
Retu rnClause of f and that of p must be compatible, as
described in sec 5.2.
The
syntax for the Statement Expression
ForkCall
JoinCall Call
FORK and
= =
= = =
JOIN statements
is straightforward: ... I JoinCall
... I ForkCall
JoinCall
FORK Call
JOIN Call
(see
sections 5,4 and 8.2.1)
The ForkCall
always returns a value (of type PROCESS) and
thus a FORK cannot
stand alone as a statement. Unlike a procedure call, which returns
a RECORD, the
value of the FORK cannot
be discarded by writing an empty extractor. The action
specified by the FORK is
to spawn a process parallel to the current one, and to begin it
executing the named procedure.
The JoinCall
appears as either a statement or an expression, depending
upon whether or not the process being joined has an empty ReturnsClause. It
has the following meaning: When the forked procedure has executed a RETURN and the JOIN is executed (in either order),
the returning process is deleted, and
the joining process receives the results, and
continues execution.
A catch phrase can be attached to either a FORK or
JOIN by
specifying it in the Call. Note. now ever. that such a catch
phrase does not catch signals incurred during the execution of the procedure:
see section 10.5.1 for further details.
There are several other important similarities
with normal procedure calls which are worth noting: The
types of all arguments and results are checked at compile time.
There is no intrinsic rule
against multiple activations (calls and/or forks) of the same procedure
coexisting at once. Of course, it is always possible to write procedures which
will work incorrectly if used in this way, but the mechanism
itself does not prohibit such use.
One expected pattern of usage of the above mechanism is to
place a matching FORK/JOIN
pair at the beginning and end of a
single textual unit (i.e. procedure, compound statement, etc.) so that the computation
within the textual unit occurs in parallel with that of the spawned process.
This style is encouraged, but is not mandatory; in fact, the matching FORK and JOIN need not even be
done by the same process. Care must be taken, of course, to
insure that each spawned process is joined only once, since the
result of joining an already deleted process is undefined. Note that the
spawned process always begins and ends its life in the same
textual unit (i.e. the target procedure of the
FORK).
While many processes will tend to follow the FORK/JOIN paradigm,
there will be others whose role is better cast as continuing provision of
services, rather than one-time calculation of results. Such a "detached"
process is never joined. If its lifetime is bounded at all, its deletion is a
private matter. since it involves neither synchronization nor
delivery of results. No language features are required for this operation; see
the runtime documentation for the description of the system procedure provided
for detaching a process.
10.2. Monitors
Generally, when two or more processes are cooperating,
they need to interact in more complicated ways than simply forking
and joining. Some more general mechanism is needed to allow orderly, synchronized
interaction among processes. The interprocess synchronization mechanism
provided in Mesa is a variant of monitors adapted
from the work of Hoare, Brinch Hansen, and Dijkstra. The underlying
view is that interaction among processes always reduces to carefully
synchronized access to shared data, and that a proper vehicle for
this interaction is one which unifies:
- the synchronization
- the shared data
- the body of code which performs the accesses
The Mesa monitor facility allows considerable
flexibility in its use. Before getting into the details. let us first look at a
slightly over-simplified description of the mechanism and a simple example. The
remainder of this section deals with the basics of monitors (more complex uses
are described in section 10.4); WAIT and
NOTIFY are
described in section 10.3.
10.2.1. In overview of monitors
A monitor is
a module instance. It thus has its own data in its global frame, and its own
procedures for accessing that data. Some of the procedures are
public. allowing calls into the monitor from outside. Obviously, conflicts
could arise if two processes were executing in the same monitor at the same
time. To prevent this, a monitor
lock is used for mutual exclusion (i.e. to insure that only one
process may be in each monitor at any one time). A call
into a monitor (to an entry
procedure) implicitly acquires its lock (waiting if
necessary). and returning from the monitor releases it. The monitor
lock serves to guarantee the integrity of the global data, which is expressed
as the monitor invariant i.e an assertion defining
what constitutes a "good state" of the data for that particular monitor.
It is the responsibility of ever)' entry
procedure to restore the monitor invariant before returning,
for the benefit of the next process entering the monitor.
Things are complicated slightly by the possibility that
one process may enter the monitor and find that the monitor
data, while in a good state. nevertheless indicates that that process cannot
continue until some other process enters the monitor and improves
the situation. The WAIT operation
allows the first process to release the monitor lock and await
the desired condition. The WAIT is
perfornied on a condition
variable, which is associated by agreement with the actual
condition needed. When another process makes that condition true, it
will perform a NOTIFY
on the condition variable, and the
waiting process will continue from where it left off (after reacquiring the
lock, of course.)
For example, consider a fixed block storage allocator
providing two entry procedures: Allocate
and Free. A
caller of Allocate may
find the free storage exhausted and be obliged to wait until some caller
of Free returns
a block of storage.
StorageAllocator: MONITOR =
BEGIN
StorageAvailable:
CONDITION; FreeList: POINTER;
Allocate: ENTRY PROCEDURE
RETURNS [p: POINTER] = BEGIN
WHILE FreeList = NIL DO
WAIT StorageAvailable
ENDLOOP;
p 4- FreeList; FreeList 4-
p. next;
END;
Free: ENTRY PROCEDURE [p: POINTER] = BEGIN
pmext 4- FreeList; FreeList 4- p; NOTIFY StorageAvailable
END;
END.
Note that it is clearly undesirable for two asynchonous
processes to be executing in the StorageAllocator at the same time.
The use of entry procedures for Allocate
and Free assures
mutual exclusion. The monitor lock is released while wAlling in Allocate in order to allow Free to be
called (this also allows other processes to call Allocate as well, leading to several
processes waiting on the queue for StorageAvailable).
10.2.2. Monitor locks
The
most basic component of a monitor is its monitor lock. A monitor lock is a predefined type, which
can be thought of as a small record:
MONITORLOCK:
TYPE = PRIVATE RECORD [locked: BOOLEAN. queue: Queue]:
The monitor lock is private: its fields are never
accessed explicitly by the Mesa programmer. Instead, it is used
implicitly to synchronize entry into the monitor code, thereby authorizing
access to the monitor data (and in some cases, other resources,
such as I/O devices. etc.) The next section describes several
kinds of monitors which can be constructed from this basic mechanism. In all of
these, the idea is the same: during entry to a monitor, it
is necessary to acquire the monitor lock by:
1.
waiting (in the queue) until: locked = FALSE.
2.
setting: locked 4-
TRUE.
10.2.3. Declaring monitor modules, ENTRY and INTERNAL procedures
In addition to a collection of data and an associated
lock, a monitor contains a set of prOcedures that do
operations on the data. Monitor ?nodules are declared much like
program or definitions modules; for example:
M: MONITOR [arguments]
= BEGIN
' • • END.
The procedures in a monitor module are of three
kinds: Entry procedures
Internal procedures
External procedures
Every
monitor has one or more entry procedures;
these acquire the monitor lock when called, and are declared as:
P:
ENTRY PROCEDURE [arguments] = . .
The entry procedures will usually comprise the
set of public procedures visible to clients of the monitor
module. (There are some situations in which this is not the case; see external
procedures, below). The usual Mesa default rules for PUBLIC and
PRIVATE procedures
apply.
Many monitors will also have internal procedures: common routines
shared among the several entry procedures. These execute
with the monitor lock held, and may thus freely access the monitor data (including
condition variables) as necessary. Internal procedures should be private, since
direct calls to them from outside the monitor would bypass the
acquisition of the lock (for monitors
implemented as multiple modules, this is not quite right;
see section 10.4, below). internal procedures can be called
only from an entry procedure or another internal procedure. They are declared
as follows:
Q:
INTERNAL PROCEDURE [arguments] = .. .
The
attributes ENTRY or
INTERNAL may
be specified on a procedure only in a monitor module. Section
10.2.4 describes how one declares an interface for a monitor.
Some monitor modules may wish to have external procedures. These are
declared as normal non-monitor procedures:
R: PROCEDURE [argumentS] = .
Such procedures are logically outside the monitor, but are
declared within the same module for reasons of logical
packaging. For example. a public external procedure might do some preliminary processing
and then make repeated calls into the monitor proper (via a private entry
procedure) before returning to its client. Being outside the monitor, an
external procedure must not reference
any monitor data (including condition variables), nor call any internal
procedures. The compiler checks for calls to internal procedures and
usage of the condition variable operations (WAIT, NOTIFY, etc.) within external
procedures, but does not check for accesses to monitor data.
A
fine point:
Actually. unchanging read-only
elobal variables may be accessed by external procedures:
it is changeable monitor data that is strictly off-limits.
Generally speaking, a chain of procedure calls involving a
monitor module has the general form:
Client procedure -- outside module
External
procedure(s) -- inside module but outside monitor
1
Entry procedure -- inside monitor
1
Internal
procedure(s) -- inside monitor
Any deviation from this pattern is likely to be a mistake.
A useful technique to avoid bugs and increase the readibility of a monitor
module is to structure the source text in the corresponding order:
M: MONITOR =
BEGIN
<External
procedures>
<Entry
procedures>
<Internal
procedures>
<Initialization (main-body) code>
END.
10.2.9. Interfaces to monitors
In Mesa, the attributes ENTRY and
INTERNAL are
associated with a procedure's body, not with its type. Thus they
cannot be specified in a DEFINITIONS module. Typically, internal procedures are not exported
anyway, although they may be for a multi-module monitor (see section 10.4.4).
In fact, the compiler will issue a warning when the
combination PUBLIC
INTERNAL occurs.
From the client side of an interface, a monitor appears to
be a normal program module, hence the keywords MONITOR and
ENTRY do
not appear. For example, a monitor Al with entry procedures P and Q might appear as:
illDefs: DEFINITIONS =
BEGIN
PROGRAM
[arguments]:
P. Q: PROCEDURE [arguments] RETURNS [results]:
END.
10.2.5. Interactions of processes and
monitors
One interaction should be noted between the process
spawning and monitor mechanisms as defined so far. If a process executing
within a monitor forked to an internal procedure of the same monitor, the
result would be two processes inside the monitor at the same time, which is the
exact situation
that monitors are supposed to avoid. The
following rule is therefore enforced:
A FORK may
have as its target any procedure except
an internal procedure of a monitor.
A fine point:
In the case of a multi-module monitor (see section
10.4.4) calls to other monitor procedures through an interface cannot be checked
for the INTERNAL attribute, since this information is not available in the
interface (see section
10.2.4).
10.3. Condition
Variables
Condition variables are
declared as:
c: CONDITION:
The content of a condition variable is private to the
process mechanism; condition variables may be accessed only via
the operations defined below. It is important to note that it is the condition variable which is the basic
construct; a condition (i.e. the contents of a condition variable) should not itself be thought of as a
meaningful object; it may not be
assigned to a condition variable, passed as a parameter, etc.
10.3.1. Wait, notify, and broadcast
A process executing in a monitor may find some condition
of the monitor data which forces it to wait until another process
enters the monitor and improves the situation. This can be accomplished using
a condition variable, and the three basic operations: WAIT, NOTIFY, and
BROADCAST, defined
by the following syntax:
Statement = WaitStmt
NotifyStmt
WaitStmt = WAIT Variable
OptCatchPhrase
NotifyStmt = NOTIFY Variable
I BROADCAST Variable
A condition variable c is always associated with
some Boolean expression describing a desired state of
the monitor data, yielding the general pattern:
Process waiting for condition:
WHILE —BooleanExpression
Do
WAIT
C ENDLOOP;
Process making condition true:
make BooleanExpression
true; -- i.e. as side effect of modifying global data
NOTIFY c:
Consider the storage allocator example from section 10.21
In this case, the desired BooleanExpression is "Freel.ist
# NIL". There
are several important points regarding WAIT and NOTIFY. some of which are
illustrated by that example:
WAIT always
releases the lock while waiting. in order to allow entry by other processes. including
the process which will do the NOTIFY (e.g. Allocate must
not lock out the caller of Free while
waiting. or a deadlock will result). Thus, the programmer is always obliged to restore
the monitor invariant (return the monitor data to a "good state")
before doing a
WAIT.
NOTIFY, on
the other hand. retains the lock, and may thus be invoked without restoring the invariant;
the monitor data may be left in in an arbitrary state, so long as the invariant
is restored before the next time the lock is released (by
exiting an entry procedure, for example).
A NOTIFY
directed to a condition variable on which no one is
waiting is simply discarded. Moreover, the built-in test
for this case is more efficient than any explicit test that the programmer
could make to avoid doing the extra NOTIFY. (Thus, in the example above,
Free always
does a NOTIFY, without
attempting to determine if it was actually needed.)
Each WAIT must be
embedded in a loop checking the corresponding condition. (E.g. Allocate, upon being notified of the S'iorageAvailable condition,
still loops back and tests again to insure that the freelist is actually
non-empty.) This rechecking is necessary because the condition, even
if true when the NOTIFY
is done, may become false again by the time the awakened
process gets to run. (Even though the freelist is always non-empty when Free does its NOTIFY, a
third process could have called Allocate
and emptied the freelist before the
waiting process got a chance to inspect it.)
Given that a process awakening from a WAIT must be careful to
recheck its desired condition, the process doing the NOTIFY can
be somewhat more casual about insuring that the condition is
actually true when it does the NOTIFY. This leads to the notion of a covering condition
variable, which is notified whenever the condition desired
by the waiting process is likely to
be true: this approach is useful if the expected cost of false alarms (i.e.
extra wakeups that test the condition and wait again) is lower
than the cost of having the notifier always know precisely what
the waiter is waiting for.
The last two points are somewhat subtle, but quite
important: condition variables in Mesa act as suggestions that their associated Boolean expressions are
likely to be true and should therefore be rechecked. They do not guarantee that a process.
upon awakening from a WAIT,
will necessarily find the condition it
expects. The programmer should never write code which implicitly assumes the truth
of some condition simply because a NOTIFY has occurred.
It
is often the case that the user will wish to notify all processes waiting on a
condition variable. This can be done using:
BROADCAST C:
This
operation can be used when several of the waiting processes should run, or when
some waiting
process should run, but not necessarily the head of the
queue.
Consider a variation of the StorageA!locator
example: StorageAllocator. MONITOR =
BEGIN
StorageAvailable: CONDITION;
Allocate: ENTRY PROCEDURE [size: CARDINAL] RETURNS [p: POINTER] = BEGIN
UNTIL <storage chunk of size words is ax
ailable> DO WAIT StorageAvailable
ENDLOOP;
p 4- <remove chunk of size words>:
END;
Free: ENTRY PROCEDURE [p: POINTER, size: CARDINAL] = BEGIN
<put back storage chunk of size words>
BROADCAST
StorageAvailable
END;
END.
In this example, there may be several processes waiting on
the queue of StorageAvailable, each
with a different size
requirement. It is not sufficient to simply NOTIFY the
head of the queue, since that process may not be satisfied with the newly
available storage while another waiting process might be. This
is a case in which BROADCAST
is needed instead of NOTIFY.
An
important rule of thumb: it is
always correct to use a BROADCAST. NOTIFY should be used instead of
BROADCAST if
both of
the following conditions hold:
It
is expected that there will typically be several processes waiting in the
condition variable queue (making it expensive to notify all of them
with a BROADCAST), and
It
is known that the process at the head of the
condition variable queue will always be the right one to
respond to the situation (making the multiple notification unnecessary);
If both of these conditions are met, a NOTIFY is
sufficient, and may represent a significant efficiency improvement
over a BROADCAST. The
allocator example in section 10.2.1 is a situation in which NOTIFY is
preferrable to BROADCAST.
As
described above, the condition variable mechanism, and the programs using it,
are intended to be robust in the face of "extra" NOTIFYS. The
next section explores the opposite problem: "missing"
NOTIFYS.
A
fine point:
When a program WAITS,
it releases the monitor lock. When it returns from the wait, it reacquires the
lock. The address of
the condition variable has to be calculated twice. If this address is obtained
by a complicated expression,
there is a subtle restriction. The address calculation cannot do a WAIT in the
same process. In other
words, consider the procedure
CondProc: PROCEDURE RETURNS [POINTER TO CONDITION]; If a program contains
the statement
WAIT CondProcnt
then
the execution of CondProc cannot WAIT.
10.3.2. Tinleouts
One
potential problem with waiting on a condition variable is the possibility that
one may wait "too long." There .are several ways this could
happen, including:
- Hardware error (e.g. "lost interrupt")
- Software error (e.g. failure to do a NOTIFY) -
Communication error (e.g. lost packet)
To handle such situations, waits on condition variables
are allowed to time out. This
is done by associating a timeout
interval with each condition variable, which limits the
delay that a process can experience on a given WAIT operation. If no NOTIFY has
arrived within this time interval, one will be generated
automatically. The Mesa language does not currently have a facility for setting
the timeout field of a CONDITION variable. See the runtime
documentation for the description of the system procedure provided
for this operation.
The waiting process will perceive this event as a normal NOTIFY. (Some
programs may wish to distinguish timeouts from normal NOTIFYS; this
requires checking the time as well as the desired condition
on each iteration of the loop.)
No
facility is provided to time out waits for monitor locks. This is because there
would be, in general, no way to recover from such a timeout.
10.4. More about Monitors
The next few sections deal with the full generality of
monitor locks and monitors.
10.4.1. The LOCKS clause
Normally,
a monitor's data comprises its global variables, protected by the special
global variable LOCK:
LOCK: MONITORLOCK;
This
implicit variable is declared automatically in the global frame of any module
whose heading is of the form:
MONITOR
[arguments]
IMPORTS
. . .
EXPORTS
. . . =
In such a monitor it is generally not necessary to mention
LOCK explicitly
at all. For more general use of the monitor mechanism, it is necessary to
declare at the beginning of the monitor module exactly which MONITORLOCK is
to be acquired by entry procedures. This declaration appears as part of
the program type constructor that is at the head of the module. The syntax is
as follows:
ProgramTC = I MONITOR ParameterList ReturnsClause
LocksClause
LocksClause :: = empty I LOCKS Expression
I
LOCKS Expression
USING identifier
: TypeSpecification
if the LocksClause is empty, entry to the monitor
is controlled by the distinguished variable LOCK (automatically supplied by the compiler).
Otherwise. the LocksClause must designate a variable
of type MONITORLOCK, a
record containing a distinguished lock field (see section 10.4.2). or a pointer
that can be dereferenced (perhaps several times) to yield one of the preceding.
if a LocksClause is present, the compiler does not generate the
variable LOCK.
If the USING clause is absent, the lock
is located by evaluating the LOCKS expression in the context of the
monitor's main body: i.e., the monitor's parameters, imports, and global
variables are visible, as are any identifiers made accessible by a global OPEN. Evaluation
occurs upon entry to, and again upon exit from, the entry
procedures (and for any WAITS in entry or internal procedures). The location
of the designated lock can thus be affected by assignments within the procedure
to variables in the LOCKS expression. To avoid disaster, it is essential
that each reevaluation yield a designator of the same MONITORLOCK. This
case is described further in section 10.4.4.
If the USING clause is present, the lock
is located in the following way: every entry or internal procedure
must have a parameter with the same identifier and a compatible type as that
specified in the USING clause. The occurrences of that identifier in the
LOCKS clause
are bound to that procedure parameter in every entry procedure (and
internal procedure doing a WAIT). The same care is necessary with respect to
reevaluation: to emphasize this, the distinguished argument is treated as a
read-only value within the
body of the procedure. See section 10.4.5 for further details.
10.4.2. Monitored records
For
situations in which the monitor data cannot simply be the global variables of the
monitor module, a monitored
record can be used:
r MONITORED RECORD [x: INTEGER, ...
A monitored record is a normal Mesa record, except that it
contains an automatically declared field of type MONITORLOCK. As
usual, the monitor lock is used implicitly to synchronize entry into the
monitor code, which may then access the other fields in the monitored record.
The fields of the monitored record must not be accessed except from
within a monitor which first acquires its lock. In analogy with
the global variable case, the monitor lock field in a monitored record is given
the special name LOCK:
generally, it need not be referred to explicitly (except
during initialization: see section 10.6).
A
fine point:
A more general form of monitor
lock declaration is discussed in section 10.4.6
CAUTION: If
a monitored record is to be passed around (e.g. as an argument to a procedure)
this should always be done by reference using a POINTER TO MONITORED RECORD. Copying
a monitored record (e.g. passing it by value) will generally lead to
chaos.
10.4.3. Monitors and module
instances
Even when all the procedures of a monitor are in one
module, it is not quite correct to think of the module and the
monitor as identical. For one thing, a monitor module, like an ordinary program
module, may have several instances. In the most
straightforward case, each instance constitutes a
separate monitor. Vlore generally, through the use of
monitored records, the number of monitors may be larger or smaller
than the number of instances of the corresponding module(s). The crucial observation
is that in all cases:
There is a one-to-one correspondence
between monitors and monitor locks.
The
generalization of monitors through the use of monitored records tends to follow
one of two patterns:
Multi-module monitors, in
which several module instances implement a single monitor. Object monitors, in
which a single module instance implements several monitors.
A fine point:
These two patterns are not
mutually
exclusive: multi-module object monitors are possible, and may occasionally prove necessary.
10.4.4. Multi-module monitors
In implementing a monitor, the most obvious approach is
to package all the data and procedures of the monitor within a single
module instance (if there are multiple instances of such a module, they
constitute separate monitors and share nothing except code.) While this will
doubtless be the most common technique, the monitor may grow too large
to be treated as a single module.
Typically, this leads to multiple modules. In this case
the mechanics of constructing the monitor are changed somewhat.
There must be a central location that contains the monitor lock for the monitor
implemented by the multiple modules. This can be done
either by using a MONITORED
RECORD or by choosing one of the modules to be the
"root" of the monitor. Consider the following example:
BigAlonRoot: MONITOR IMPORTS
... EXPORTS... = BEGIN
monitorDatuml: monitorDatum2:
pl: PUBLIC ENTRY
PROCEDURE...
END.
BigMonA: MONITOR
LOCKS root -- could equivalently say root.LOCK
IMPORTS
root: BigAlonRoot .. EXPORTS ... SHARES
BigAlonRoot = BEGIN
.. •
p2:
PUBLIC ENTRY PROCEDURE ...
x <- root.monitorDatuml: -- access
the protected data of the monitor
END.
BigMonB: MONITOR
LOCKS root
IMPORTS
root: BigAlonRoot . EXPORTS ... SHARES
BigAfonRoot = BEGIN OPEN root:
• • •
p3:
PUBLIC ENTRY PROCEDURE .
monitorDatum2 <- -- access the protected data
via an OPEN
END.
]lie monitor BigMon
is implemented by three modules. The modules BigtlfonA and BigAlonR have a
LOCKS clause
to specify the location of the monitor lock: in this case, the distinguished
variable LOCK in
BVIonRoot. When
any of the entry procedures pl, p2. or p3 is called, this lock is acquired
(waiting if necessary), and is released upon returning. The reader can verify
that no two independent processes can be in the monitor at the same time.
Note that since the LOCK field is private in BigillonRoot. the modules BigillonA and BigAlonB must SHARE BigAlonRoot. Another way to
accomplish access to the lock would be to specify a PUBLIC GlobalAccess (sec.
7.5) for BigMonRoot.
Another means of implementing multi-module monitors is by
means of a MONITORED
RECORD. Use of OPEN allows the fields of the record to be referenced without
qualification. Such a monitor is written as:
AlonitorData: TYPE = MONITORED
RECORD [x: INTEGER, ... AlanA: MONITOR [pm: POINTER TO MonitorData]
LOCKS pm
IMPORTS .
EXPORTS
... =
BEGIN OPEN pm;
P: ENTRY PROCEDURE 1..1 = BEGIN
x x+ 1: -- access to a monitor variable END;
END.
The LOCKS clause in the heading of this module (and each other
module of this monitor) leads to a MONITORED RECORD. Of course, in all such
multi-module monitors. the LOCKS clause will involve one or more levels of
indirection (POINTER
TO MONITORED RECORD, etc.) since passing a monitor lock by
value is not meaningful. As usual, Mesa will provide one or more
levels of automatic dereferencine as needed.
More
generally, the target of the LOCKS clause can evaluate to a MONITORLOCK (i.e. the example above
is equivalent to writing "LOCKS pm.LOCK").
CAUTION: The
meaning of the target expression of the LOCKS clause must not change between the call to the entry procedure
and the subsequent return (i.e. in the above example, changing pm would invariably
be an error) since this would lead to a different monitor lock being released
than was acquired, resulting in total chaos.
There are a few other issues regarding multi-module
monitors which arise any time a tightly coupled piece of Mesa code
must be split into multiple module instances and then spliced back together.
For example:
If
the lock is in a MONITORED
RECORD. the monitor data will probably need to be in the record
also. While the global variables of such a multi-module monitor are covered by
the
monitor lock, they do not constitute monitor data in
the normal sense of the term. since they are not uniformly
visible to all the module instances.
Making the internal procedures of a multi-module monitor PRIVATE will
not work if one module wishes to call an internal procedure in another module.
(Such a call is perfectly acceptable so long as the caller already holds the
monitor lock). Instead. a second interface (hidden from the
clients) is needed as part of the "glue" holding the monitor
together. Note however, that Mesa cannot currently check that
the procedure being,
called through the interface is an internal one (see section
10.2.4).
A fine point:
The compiler will complain about the
PUBLIC INTERNAL procedures. but this is just a warning.
•
10.9.5. Object monitors
Some applications deal with objects, implemented, say, as records
named by pointers. Often it is necessary to insure that
operations on these objects are atomic,
i.e., once the operation has begun, the object will not be
otherwise referenced until the operation is finished. If a module instance
provides operations on some class of objects, the simplest way of guaranteeing
such atomicity is to make the module instance a monitor. This is
logically correct, but if a high degree of concurrency is expected, it may
create a bottleneck; it will serialize the operations on all objects in the class, rather
than on each of
them individually. If this problem is deemed serious, it can be solved by implementing
the objects as monitored records, thus effectively creating a separate monitor
for each object. A single module instance can implement the
operations on all the objects as entry procedures, each taking as a
parameter the object to be locked. The locking of the parameter is specified
in the module
heading via a LocksClause with
a USING clause.
For example:
ObjectRecord: TYPE = MONITORED
RECORD [ . . . ];
ObjectHandle: TYPE = POINTER TO
ObjeciRecord:
ObjectManager. MONITOR [arguments]
LOCKS object
USING object:
ObjectHandle
IMPORTS
. . .
EXPORTS
. . . =
BEGIN
Operation: PUBLIC ENTRY
PROCEDURE [object: ObjectHandle,
BEGIN
. . .
END;
. . .
END.
Note that the argument of USING is evaluated in the scope
of the arguments to the entry procedures. rather than the global scope
of the module. In order for this to make sense, each entry procedure, and each
internal procedure that does a WAIT, must have an argument which matches exactly the name
and type specified in the USING subclause. All other components of the argument
of LOCKS are
evaluated in the global scope, as usual.
As
with the simpler form of LOCKS clause, the target may be a more complicated expression
and/or may evaluate to a monitor lock rather than a monitored
record. For example:
LOCKS p.q.LOCK USING p: POINTER TO ComplexRecord . .
CAUTIO\: Again.
the meaning of the
target expression of the
LOCKS clause
must not change
between the call to the entry
procedure and the subsequent return. (I.e. in the above example, changing
p or p.q would almost surely be an
error.)
CAUTION:
It is important to note that global variables of object monitors
are very dangerous: they are not covered
by a monitor lock, and thus do not constitute
monitor data. If used at all, they must be set only at module initialization time and must
be read-only thereafter.
10.9.6. Explicit declaration of monitor
locks
It is possible to declare monitor locks explicitly:
nyLock: MONITORLOCK;
The normal cases of monitors and monitored records are
essentially stylized uses of this facility via the automatic
declaration of LOCK, and should cover all but the most obscure
situations. For example, explicit delarations are useful in
defining MACHINE
DEPENDENT monitored records. (Note that the LOCKS clause
becomes mandatory when an explicitly declared monitor lock is used.) More generally,
explicit declarations allow the programmer to declare records with several
monitor locks, declare locks in local frames, and so on: this
flexibility can lead to a wide variety of subtle bugs, hence
use of the standard constructs whenever possible is strongly advised.
10.4.7 Milne
ENTRY procedures
The syntax for definitions modules allows the specification
of a LOCKS clause.
This is to allow inline ENTRY PROCEDURES to be declared in the interface. In order for
this to make sense, the monitor lock must be an interface
variable, or the procedures must deal with an object style monitor. No special restrictions
(other than those that apply to all INLINE bodies) need be met when
declaring inline ENTRY PROCEDURES within the program module of a monitor.
10.5. Signals
10.5.1. Signals
and processes
Each process has its own call stack, down which signals propagate.
If the signaller scans to the bottom of the stack and
finds no catch phrase, the signal is propagated to the debugger. The important
point to note is that forking to a procedure is different from calling it. in
that the forking creates a gap across which signals cannot
propagate. This implies that in practice, one cannot casually
fork to any arbitrary procedure. The only suitable targets for forks are
procedures which catch any signals they incur, and which never
generate any signals of their own. •
10.5.2. Signals and monitors
Signals require special attention within the body of an entry
procedure. A signal raised with the monitor lock held will propagate
without releasing the lock and possibly invoke arbitrary computations.
For errors, this can be avoided by using the RETURN WITH ERROR construct.
RETURN
WITH ERROR NoSuchObject:
Recall
from Chapter 8 that this statement has the effect of removing the currently
executing frame from the call chain before issuing the ERROR. If
the statement appears within an entry procedure,
the monitor lock is released before the error is
started as well. Naturally, the monitor invariant must be restored before this operation is performed.
For example, consider the following program
segment: Failure:
ERROR
[kind: CARDINAL] = CODE:
Prof: ENTRY PROCEDURE
[. . .] RETURNS [cl, c2: CHARACTER] = BEGIN
ENABLE
UNWIND => . .
. . .
IF condl
THEN ERROR Failure[1];
IF cond2 THEN RETURN WITH ERROR Failure[2]:
END;
Execution
of the construct ERROR
Failure[1] raises
a signal that propagates until some catch phrase specifies an exit.
At that time, unwinding begins: the catch phrase for UNWIND in
Proc is
executed and then Proc's
frame is destroyed. Within an entry procedure such as Proc, the lock is held until the
unwind (and thus through unpredictable computation performed by catch phrases).
Execution of the construct RETURN WITH ERROR Failure[2] releases the monitor lock and destroys the frame
of Proc before
propagation of the signal begins. Note that the argument list in this construct
is determined by the declaration of Failure
(not by Proc's
RETURNS clause).
The catch phrase for UNWIND
is not executed in this case. The signal Failure is actually raised by the
system, after which Failure propagates
as an ordinary error (beginning with Proc's caller).
When
the RETURN WITH ERROR construct
is used from within an internal procedure, the monitor lock is
not released;
RETURN WITH ERROR will
release the monitor lock in precisely those cases that
RETURN
will.
Another
important issue regarding signals is the handling of UNWINDS; any
entry procedure that may experience an UNWIND must catch it and clean up
the monitor data (restore the monitor invariant):
P: ENTRY PROCEDURE [ ] =
BEGIN ENABLE UNWIND => BEGIN <restore
invariant> END;
•
END;
At the end of the UNWIND catchphrase, the compiler
will append code to release the monitor lock before the frame is unwound. It is
important to note that a monitor always has at least one cleanup task
to perform when catching an UNWIND signal: the monitor lock must be released. To
this end, the programmer should be sure to place an
enable-clause on the body of every entry procedure that might
evoke an UNWIND (directly
or indirectly). If the monitor invariant is already satisfied, no further
cleanup need be specified, but the
null catch-phrase must be written so that the compiler will generate
the code to unlock the monitor:
BEGIN
ENABLE UNWIND => NULL;
This should be omitted only when it is certain that no UNWINDS can
occur.
Another
point is that signals caught by the OptCatchPhrase of a WAIT operation should be
thought of as occurring after reacquisition of the
monitor lock. Thus, like all other monitor code,
'catch phrases within a monitor arc always executed with
the monitor lock held.
10.6. Initialization
When a new monitor comes into existence. its monitor data
will generally need to be set to some appropriate initial values;
in particular. the monitor lock and any condition variables must be initialized.
As usual. Mesa takes responsibility for initializing,
the simple common cases; for the cases not handled automatically,
it is the responsibility of the programmer to provide appropriate initialization
code, and to arrange that it be executed at the proper time. The two types of initialization
apply in the following
situations:
Monitor data in global variables can be initialized using
the normal Mesa initial value constructs in declarations.
Monitor locks and condition variables in the global frame will also
be initialized automatically (although in this case, the programmer does not
write any explicit initial value in the declaration).
Monitor data in records must be initialized by the
programmer. System procedures must be used to initialize the monitor lock and
condition variables. See the runtime documentation for
the descriptions of appropriate procedures.
A fine
point:
If a variable containing
a record is declared in a frame. it is normally possible to initialize it in
the declaration (i.e.
using a constructor as the initial value): however. this does not apply if the record contains monitor locks or condition variables, which must be initialized
via calls to system procedures.
Since initialization code modifies the monitor data, it
must have exclusive access to it. The programmer should insure
this by arranging that the monitor not be called by its client processes until
it is ready for use.
APPENDIX A. Pronouncing Mesa
The
following suggestions may be helpful in reading Mesa programs:
![Text Box: For =7
4-
n: T ?afield
P1'
gx [a.. b] [a.. b) (a..b] (a.b)
FOR i I. k f[x, y, z]](23a-MesaManualOCR_files/image073.gif) Read
Read
chooses
gets
11 is a T
nis field
p's referent
address
of x
(the
interval) a through
b
(the
interval) a up
to b
(the
interval) above a through
b (the
interval) above a up
to b for
i getting
first j, thereafter
k f of x,
y and z
enabling
We
leave as an exercise for the reader the following statement, attributed to
Oscar Hammerstein II. 4- weary AND Siek[trying];
APPENDIX B. Programming Conventions
The Mesa compiler only uses blanks. TABS, and
carriage returns as separators for basic lexical units such
as identifiers: extra ones do not hurt. Furthermore, it allows you to write
identifiers in any combination of upper and lower case letters: the
identifiers Alpha. ALPHA, alpha and AlphA are all legal
(but different) Mesa
identifiers. It is recommended that you adhere to a standard set of conventions
for constructing identifiers and laying out programs. The
recommended conventions are summarized below.
B.1.
Names
Most
identifiers should be written in lower case, except that the first letter of
each new "word" in the identifier should be
capitalized. Thus,
line
firstLine
firstLinePos
This
convention makes it easy to read identifiers which are made up of several
words. (Note that Mesa does not allow spaces in identifiers.)
Capitalize the first letter of type identifiers, procedure
names, signal names, and module names.
The
following convention for constructing names has been used sucrPcsfully to
reflect their types:
Choose a short (2-3 character) tag
for
each "basic type" you use: e.g., In for Line and co for Coordinate.
You can
use the tag as the type name, or not. as you prefer. If you
do. capitalize it.
Use the following prefixes to
construct tags for "derived" types (most of them reflect the intended
use of some underlying type).
p -
pointer: pLn = pointer to a line
i -
index: iLn = index in an array of lines. I - length
n -
number of items (total or count)
Whether to use a prefix or to
invent a new type tag, is a matter of judgment: depending on whether it is better to emphasize the
relationship of this type to another, or to emphasize its individuality.
If
you need only one name of a given type in a scope, use the tag as its name:
In :
Ln:
pLn :
POINTER TO Ln.
If you need several names, append modifiers
to
the tag (avoid simple numbers like 1. 2. etc.): InOld, InNew, InBuffer: Ln.
The
advantages of this scheme are three-fold:
the reader spends less time looking up the types of identifiers:
the
writer spends less time thinking up names:
if you have forgotten a name,
there is a good chance you will be able to guess it correctly if you know the tag vocabulary.
B.2.
Layout
Write
statements one per line, unless several simple statements which together perform a single function will fit on one line.
Indent the labels of a SELECT (including the ENDCASE) one
level, and the statements a second level (unless a statement will fit on the same line with the
label).
Indent one level for the statement following a THEN or ELSE (unless it fits on
the same line). Put THEN
on the same line with IF, and don't indent ELSE with respect to IF. If the statement
following ELSE is
another IF, write
both on the same line.
Indent one level for each compound BEGIN-END,
DO-ENDLOOP, or bracket pair in a record declaration. When
the rules for IF and SELECT call for indenting a
statement. do not indent an extra level for a
BEGIN.
It is fine to put a compound statement or loop on a single line if it will fit.
If a statement won't fit on a single line, indent
the continuation
line(s) by two spaces.
Among
other things, these rules have the property that they allow a program to be
easily converted to a form in which the bracketing is implied by
the indentation.
B.3. Spaces
The following
rules for spaces should be broken when necessary, but are a good general guide:
A space after a comma, semicolon, or colon, and none
before
No spaces inside brackets or parentheses
No spaces around single-character operations: *, -, etc., except for
4-
APPENDIX C. Alto/Mesa Machine
Dependencies
This
appendix contains a number of machine-dependent constants and definitions for
the Alto implementation of Mesa.
C I. Numeric limits
On the Alto. the numeric limits are the following:
|
FIRST[INTEGER]
|
=
|
—
32768 = — 215
|
and has internal representation
|
100000B
|
|
LAST[INTEGER]
|
=
|
32767
|
= 215
— 1
|
and has internal representation
|
077777B
|
|
LAST[CARDINAL]
|
=
|
65535
|
= 216-1
|
and has internal representation
|
177777B
|
|
FIRST[LONG
INTEGER] LAST[LONG INTEGER] LAST[LONG CARDINAL]
C.2. AlioDefs
|
= — 2147483648 = 231 = 2147483647 = 231-1
= 4294967295 = 232-1
|
|
|
|
|
|
|
|
A
module similar to the one below is a part of the Alto/Mesa system and defines
several useful constants.
|
Aitobefs: DEFINITIONS = BEGIN
wordlength: INTEGER = 16; --
maxword: CARDINAL =
177777B; maxinteger: INTEGER =
077777B;
|
Alto word length (bits)
-- N.B. negative as 16 bit
integer -- maximum
positive number
|
charlength: INTEGER = 8; -- Alto character
size (bits)
maxcharcode: INTEGER = 377B; BYTE: TYPE = [0..maxcharcode];
BytesPerWord, CharsPerWord: INTEGER = wordlength/charlength;
LogBytesPerWord. LogCharsPerWord: INTEGER = 1;
PageSize: INTEGER = 256; -- Alto page size (words)
LogPageSize: INTEGER = 8;
BytesPerPage, CharsPerPage: INTEGER = PageSizeCharsPerWord;
LogBytesPerPage. LogCharsPerPage: INTEGER = LogPageSize +
LogCharsPerWord;
VMLimit: CARDINAL = 1777776; -- maximum Alto VM address
Address: TYPE = [0..VMLimit];
MaxVMPage: INTEGER = 255; -- maximum Alto VM page
number MaxFifePage: CARDINAL = 077777B;
PageNumber:
TYPE = [0..MaxFilePage];
PageCount: TYPE = [O..MaxVMPage + 1];
END.
C.3. ASCII character set and
ordering of character values
The following list gives the characters of the ASCII
character set in increasing order, accompanied by their literal
representations. Control characters are represented as fa. In addition, a
number of special characters such as SP (space), DEL (rubout) are
denoted by their generally accepted names.
Octal Character Octal Character
Value Name(s) Value Name(s)
 NUL
NUL
TA
TB tC tD rE tF
TG, BELL
tH. BS
1'1
tJ, LF
tK tL
tM, CR
tN tO
tP
tQ tR tS tT tU
tV tW
tX
tY tZ ESC
' .
SPace
.# 'S '&
a single quote
')
,*
•
'> '0
'2
'3
'4
'5
'6
'7
'8
'9
100C
101C .(a_.
'A
1020 'B
103C
'C
104C 'D
105C 'E
106C
107C 'F
'G
1100
1110 'H
'I
111132CC -.1
114C K
'L
1150 'M
116C 'N
117C '0
120C 'P
121C
12223C R
123C 'Q
'
124C 'S
'T
125C
'U
126C 'V
127C 'W
130C 'X
131C 'Y
132C
133C 'Z
134C
135C 1
']
136C
137C 't
14°C
141C ' 4-
'a
142C :cb
143C
11445C 'd
C '
'e
114476CC 'f
.g
150C
151C h
152C 'i
'
153C j
'k
154C
155C '1
'm
156C 'n
157C 'o
160C
'p
161C .
162C r
163C .
G1
,
164C t
C 's
:u
166C
167C i;
170C ,w
171C 'z
172C 'x
173C '
174C '{
175C 1
1
176C
177C
DEL
174 Appendix
C: Alto/Mesa Machine Dependencies
C.4. it
lto/Alesa STRING procedures
A
module similar to the one below is a part of the Alto/Mesa system and defines
useful procedures provided by the system for operating on strings.
See the system documentation for its exact form.
DIRECTORY
AltoDeis: FROM "aItodets";
StringDefs:
DEFINITIONS = BEGIN
--COMPILE-TIME
CONSTANTS AND TYPES
SubStringDescriptor: TYPE = RECORD [ base: STRING,
offset.
length: CARDINAL];
SubString: TYPE = POINTER TO SubStringDescriptor;
--INTERFACE
ITEMS
Overflow:
SIGNAL;
lnvalidNumber:
SIGNAL;
StringBoundsFault: SIGNAL [s: STRING] RETURNS [ns: STRING];
WordsFdrString: PROCEDURE [nchars: CARDINAL] RETURNS [CARDINAL];
AppendChar: PROCEDURE [s: STRING, c: CHARACTER];
AppendString: PROCEDURE [to,from: STRING];
EqualString, EqualStrings: PROCEDURE [st s2: STRING] RETURNS [BOOLEAN]; EquivalentString.
Equivalent Strings: PROCEDURE
[Si,
s2: STRING] RETURNS
[BOOLEAN];
AppendSubString: PROCEDURE[to: STRING, from: SubString];
EqualSubString, EqualSubStrings: PROCEDURE [sl. s2: SubString] RETURNS [BOOLEAN]; EquivalentSubString.
EquivalentSubStrings: PROCEDURE
[sl,
s2: SubString] RETURNS
[BOOLEAN]; DeleteSubString: PROCEDURE [s: SubString];
UpperCase. LowerCase: PROCEDURE [CHARACTER] RETURNS
[CHARACTER];
StringToDecimal: PROCEDURE [STRING] RETURNS [INTEGER];
StringToOctal: PROCEDURE [STRING] RETURNS [UNSPECIFIED];
StringToNumber: PROCEDURE [s: STRING. radix: CARDINAL] RETURNS [UNSPECIFIED]; StringToLong Number: PROCEDURE [s: STRING, radix: CARDINAL] RETURNS [LONG UNSPECIFIED];
AppendDecimal: PROCEDURE [s: STRING, n: INTEGER];
AppendOctal: PROCEDURE [s: STRING, n: UNSPECIFIED];
AppendNumber:
PROCEDURE [5: STRING, n: UNSPECIFIED.
radix:
CARDINAL]; AppendLongDecimal: PROCEDURE [s: STRING, n: LONG INTEGER];
AppendLongNumber: PROCEDURE [s: STRING, n: LONG UNSPECIFIED, radix: CARDINAL];
END.
APPENDIX I).
Binder Extensions
The Alto implementation of the Mesa hinder
provides two extensions for controlling the space occupied by Mesa programs at
runtime. These are specified with the CPacking and CLinks clauses (section 7.7).
D.I. Code
packing
It is possible to pack together the code for several
modules into a single segment. This is useful for two
reasons:
Since the code is allocated an integral number of pages,
there is some wasted space in the last page
("breakage"). If several modules are combined into a single segment,
the breakage is amortized over all the modules, and there is
less waste on the average.
All the modules will be brought into and out of memory
together, as a unit: a reference to any module in the pack will cause all the
code to be brought in. Modules which are tightly coupled dynamically are good
candidates for packing (for example, resident code should probably
always be packed).
Of course, it is possible to "over pack" a
configuration; the segments might become so large that there
will never be room in memory for more than one of them at a time (this should
remind you of an overlay system). Packing is a tradeoff and should be used with
caution.
D.I.1. Syntax
The segments are specified at the beginning of the
configuration by giving a list of the modules which comprise each
one. Any number of PACK statements
may appear. The scope of the packing specification is the whole configuration,
and not subconfigurations or individual module instances, because
there is at most one copy of a module's code in any configuration.
ConfigDescription
= Directory CPacking Configuration .
CPacking = empty I CPackSeries ;
CPackList = PACK IdList
CPackSeries = CPackList I CPackSeries ; CPackList
Each PackList
defines a single segment; the code for all the modules in
the IdList will
be packed into it. The identifiers in the IdList must refer to modules in the
configuration, and not to module instances: it is the code
and not the global frames that are being packed (the frames are always
packed when
they are allocated by the loader).
It is illegal to specify the same module in more than one
PackList. Even
though there may be multiple instances of the module (i.e., multiple
global frames) in the configuration, the code is shared by all of
them, and therefore can only appear in one pack.
Finally, it is perfectly fine to reach inside a previously
bound configuration that is being instantiated and single out
some or all of its modules for packing. Of course, you must know something
about the structure of that configuration in order to do this.
D.I.2. Restrictions
Obviously, the PACK statements apply only if
the code is being moved to the output file: otherwise. the
pack lists are ignored (and no warning message is given). This allows the
programmer to debug the configuration without shuffling the code from file to
file. thereby saving time. When making the final version, the packing
can be effected with a binder switch. without having to modify the source of
the configuration
description.
Once
some modules have been packed together, they cannot be taken apart and repacked
with other modules later on. when they are bound into
some other configuration.
Fine
point:
If a previously bound
confizuration contains a pack, referencing any module of the pack gets the whole thing. So it is possible to pack a module
and a pack together. or even to pack two packs. It is never possible to unpack a pack.
In general. code packing should be specified only to the
extent that no unpacking will ever-be desired. Once the
packing is done, it can't be undone, unless you start over with the individual modules.
D.2. External
links
In previous Mesa systems, links to the externals
referenced by a program (imported procedures, signals, errors, frames, and
programs) were always stored in the module's global frame. This allows each
instance of a module to be bound differently, and it allows binding to be done
at runtime without modification of the module's code segment. However,
it has two drawbacks:
The
links are only referenced by the module's code, and are therefore not needed
when the code is swapped out. Hence, the links logically belong in
the code segment.
If two instances of a module are bound identically (the
usual case), the links must be stored twice.
Fine
Point:
To
determine the amount of space required for external links, see the compiler's
typescript file. Each link occupies one word.
The
Mesa binder optionally places links in the code segment. This option is enabled
by constructs in the configuration language, and is further
controlled by binder and loader switches.
D.2.1. Syntax
For
each component of a configuration, the link location is specified using the LINKS construct
defined below. The default is frame links.
CLinks =
empty I LINKS : CODE I LINKS : FRAME
A link specification can optionally be attached to each
instantiation of a module, overriding the current default, so that the link location can be
different for each. instance.
CRightSide = Item I Item
[] CLinks I Item [ IdList CLinks
Alternately. the link option can be specified in the
configuration header. This merely changes the default option for
the configuration:
it will apply to all components (including nested configurations)
unless it is explicitly overridden.
CHead = CONFIGURATION CLinks Imports CExports ControlClause
This construction works much like the PUBLIC / PRIVATE options
in Mesa,
and it nests in the same way. A link option attached to a configuration
changes the default for all components within it, but that
default can he overriden for a particular module (or nested configuration) by
specifying a different link option.
D.2.2. Restrictions
This
scheme has the consequence that, if
a module with code links has multiple instances. each instance must be bound the same.
As with code packing, the code links option takes effect
only when the code is being moved to 'the output file. At this point,
the binder will make room for the links as it copies the code if any module
sharing that code has requested code links. Again, this allows a programmer to
debug without the expense of moving the code (using frame
links), and then to effect the code links option with a binder
switch, without changing the source of the configuration description.
Fine
point:
Once space for code
links has been added to a configuration, it cannot be undone by a later binding.
On the other hand,
space for code links can always be added to a (previously bound) configuration,
even if it did not specify code links in
its description.
Using code links has one drawback: it slows down the
binding and loading process, as the code must be swapped in and
rewritten. The binder must make room in the code segment for the links, as described
above. And because the loader resolves imports of previously loaded modules, as
well as the imports of the module being loaded, it may have to swap in
(and perhaps update and swapout) the code segment for every
module in the system.
Because
of the overhead involved, the loader will not automatically attempt to use code
links, even if the space is available in the code segment. A
loader switch must be used to effect this option.
Documentation of binder and loader switches in in the Mesa User's Handbook.
APPENDIX E. Mesa Resered Words
Listed
below are all of the Mesa reserved words. Words marked with an astrisk are predeclared rather than reserved. Predeclared
identifiers can be redefined (hut seldom should be).
ABS
ALL
AND
ANY
ARRAY 4-701
BASE
BEGIN
·
BOOLEAN - BROADCAST
·
CARDINAL CHARACTER
CODE COMPUTED
·
CONDITION •
·
CONTINUE co
t.:5
DECREASING DEFINITIONS DEPENDENT
DESCRIPTOR DIRECTORY
DO
ELSE ENABLE
END
EN DCASE
EN DLOOP
ENTRY - ERROR - EXIT
EXITS EXPORTS
FALSE
- FINISHED
- FIRST
FOR
FORK FRAME FROM GO
- GOTO IF
IMPORTS
IN
INLINE
- INTEGER wt.
INTERNAL
'sr-0 k..
·
JOIN
LAST
LENGTH
LOCKS uST
·
LONG - LOOP LOOPHOLE
MACHINE
- MAX
- MIN
.MOD
MONITOR
MONITORED
· MONITOR LOCK •
·
NEW VON.)
NIL •
NOT
· NOTIFY
NULL
OF
OPEN
· OR
ORDERED
OVERLAID
PACKED
- POINTER
- PORT
PRIVATE
· PROCEDURE
· PROCESS
· PROGRAM
PUBLIC
READONLY
 REAL • RECORD
REAL • RECORD
· RELATIVE REPEAT RESTART RESUME RETRY
· RETURN RETURNS SELECT SHARES - SIGNAL SIZE
START STATE STOP
STRING StringBody` THEN THROUGH
TO
TRANSFER
TRUE
• TYPE
· UNSPECIFIED` UNTIL UNWIND* USING WAIT
WHILE WITH
WORD*
APPENDIX F. Collected Grammar
Die Mesa grammar in this section is a
collected version of the grammar distributed throughout the body of the Manual.
There arc some differences, primarily due to the Manual's grammar being distorted
for purposes of exposition. This one is
intended to be internally consistent.
The
grammar is divided into four parts. corresponding to the syntax for
CompilationUnit. TypeSpecification, Statement, and Expression.
These four parts refer to each other and occasionally use syntax piles from other
parts (such as LeftSide.
which is used in an assignment statement
but defined under Expression). Where such cross references occur, a comment has
been added to indicate which part to refer to. Other than this. each part is
self-contained. and the productions within a part have been ordered
alphabetically by their names, except that the productions for
CompilationUnit, TypeSpecification, etc. head their respective sections.
CompilationUnit
Directory
identifier : ModuleHead =
GlobalAccess ModuleBody
 empty I DIRECTORY IncludeList ; empty I EXPORTS IdList
empty I DIRECTORY IncludeList ; empty I EXPORTS IdList
stringLiteral
Access
-- in TypeSpecification identifier I IdList , identifier empty I IMPORTS InterfaceList
identifier : FROM
FileName UsingClause I
IncludeList
identifier : FROM FileName UsingClause
identifier I identifier :
identifier
Interfaceltem
I InterfaceList ,
Interfaceltem Block . -- in Statement
ProgramTC ImportsList ExportsList
ShareList I DefinitionTC ImportsList ShareList
empty I [ NamedFieldList --
in TypeSpecification
empty
I SHARES IdList
empty
I USING [ IdList


 PredefinedType I Typeldentifier I TypeConstructor
PredefinedType I Typeldentifier I TypeConstructor
 empty I PUBLIC I PRIVATE
identifier
empty I PUBLIC I PRIVATE
identifier
PackingOption
ARRAY IndexType OF TypeSpecification empty I BASE
Expression
I ByteList ,
Expression empty I NamedFieldList
Expression
I ConstantList ,
Expression empty I F DefaultSpecification
empty I
Expression I
NULL I
Expression I NULL
 DEFINITIONS I DEFINITIONS LocksClause
DEFINITIONS I DEFINITIONS LocksClause
 DESCRIPTOR FOR ReadOnlyOption TypeSpecification I
DESCRIPTOR FOR ReadOnlyOption TypeSpecification I
DESCRIPTOR FOR ReadOnlyOption
PackingOption ARRAY OF TypeSpecification
INTEGER I CARDINAL I CHARACTER I
BOOLEAN I EnumerationTC
I SubrangeTC
{
IdList }
[
UnnamedFieldList I [ NamedFieldList
ElementType
I Typeldentifier empty I INLINE
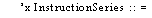 empty I ByteList I
ByteList ; Inst ructionSeries
empty I ByteList I
ByteList ; Inst ructionSeries
 [ Expression .. Expression II [ Expression ..
Expression ) ( Expression .. Expression ) ( Expression .. Expression )
[ Expression .. Expression II [ Expression ..
Expression ) ( Expression .. Expression ) ( Expression .. Expression )
empty
I
LOCKS Expression I
LOCKS
Expression USING identifier : TypeSpecification
LONG
TypeSpecification
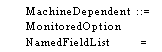 MACHINE CODE BEGIN
InstructionSeries END -- not described in this manual empty I MACHINE
DEPENDENT
MACHINE CODE BEGIN
InstructionSeries END -- not described in this manual empty I MACHINE
DEPENDENT
empty
I MONITORED
IdList
: Access TypeSpecification DefaultOption I

 TO ReadOnlyOption TypeSpecification TO FRAME [ identifier ]
TO ReadOnlyOption TypeSpecification TO FRAME [ identifier ]

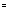 Ordered BaseOption POINTER Optionallnterval
PointerTail
Ordered BaseOption POINTER Optionallnterval
PointerTail
 PORT ParameterList ReturnsClause I RESPONDING PORT ParameterList ReturnsClause
PORT ParameterList ReturnsClause I RESPONDING PORT ParameterList ReturnsClause
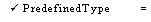 INTEGER I CARDINAL I LONG INTEGER
I REAL I BOOLEAN I
CHARACTER I STRING I MONITORLOCK I
CONDITION I
INTEGER I CARDINAL I LONG INTEGER
I REAL I BOOLEAN I
CHARACTER I STRING I MONITORLOCK I
CONDITION I
UNSPECIFIED I WORD

 InlineOption Block Block in Statement
InlineOption Block Block in Statement
PROCEDURE ParameterLisi ReturnsClause PROCESS ReturnsClause
 PROGRAM ParameterList ReturnsClause
PROGRAM ParameterList ReturnsClause
MONITOR
ParameterList ReturnsClause LocksClause
 empty I READONLY
empty I READONLY
MonitoredOption
MachineDependent RECORD [ VariantFieldList
 Typeldentifier RELATIVE TypeSpecification Typeldentifier RELATIVE LONG TypeSpecification
Typeldentifier RELATIVE TypeSpecification Typeldentifier RELATIVE LONG TypeSpecification
 empty I RETURNS FieldList
empty I RETURNS FieldList
SIGNAL
I ERROR
SignalOrError
ParameterList ReturnsClause Interval I Typeldentifier Interval
identifier : Access TagType COMPUTED TagType
OVERLAID
TagType
 TypeSpecification
I*
TypeSpecification
I*
DescriptorTC I A rrayTC I
EnumerationTC I LongTC Pointe
rTC PortTC I ProcedureTC I ProcessTC RecordTC I RelativeTC I SignaITC I SubrangeTC

 identifier I
identifier I
identifier
. identifier I
 Adjective
Typeldentifier
Adjective
Typeldentifier
TypeSpecification
UnnamedFieldList
, TypeSpecification
IdList => [ VariantFieldList ] , IdList = > NULL ,
CommonPart identifier : Access VariantPart I VariantPart I
Named Field List I
UnnamedFieldList
empty
 Variant I VariantList Variant
Variant I VariantList Variant
SELECT Tag FROM VariantList
ENDCASE
·  • 1.,1
• 1.,1
·
• —
AssignmentStmt I
Block I Call I
ContinueStmt I
ExitStmt I GotoStmt I IfStmt I
JoinCall
I LoopCloseStmt I JoinCall
in Expression
LoopStmt I Notify I NullStmt
ResumeStmt I RetryStmt
I ReturnStmt I SelectStmt SignalCall I StartCall
I RestartStmt I
StopStmt I WaitStmt





![Text Box: LeftSide 4- RightSide I LeftSide, RightSide in Expression
Extractor f RightSide
BEGIN
OpenClause
EnableClause
DeclarationSeries StatementSeries ExitsClause
END
Variable I -- in Expression
Variable [ ComponentList ComponentList in Expression
Variable [ ComponentList CatchSeries
Variable [ ! CatchSeries]
ExpressionList => Statement ExpressionList in Expression
Catch I ANY => Statement
Catchltem I Catch ; CatchSeries
AdjectiveList => Statement :1 ChoiceSeries AdjectiveList => Statement ;
BEGIN
Body
ExitsClause END
empty I WHILE Expression I UNTIL Expression CONTINUE
IdList :
Access -- Access in TypeSpecification
ReadOnlyOption EntryOption ReadOnlyOption in TypeSpecification
TypeSpecification
Initialization ; I
IdList : Access TYPE = Access TypeSpecification ;
empty I DeclarationSeries Declaration empty I DECREASING
empty I ELSE Statement
ENABLE Catchltem ; I
ENABLE BEGIN CatchSeries END ;](23a-MesaManualOCR_files/image114.gif) Adjective I
AdjectiveList , Adjective -- in TypeSpecification FOR identifier «- Expression , Expression
Adjective I
AdjectiveList , Adjective -- in TypeSpecification FOR identifier «- Expression , Expression
x
x
ENABLE BEGIN CatchSe ries ; END ; empty
 empty I ENTRY
empty I ENTRY
ERROR
Call I ERROR
empty
I EXITS I EXITS ExitSeries I EXITS ExitSeries ;
La
belList => Statement I
ExitSe
ries ; LabelList => Statement
EXIT
empty
I Left Side
[ Keywo rdExt ractList ] I [ PositionalExt ractList
empty
I => Statement
FINISHED
=> Statement I FINISHED => Statement ;
GOTO
Label I GO TO Label
IF
Expression THEN Statement ElseClause
Expression
I
ProcedureBody I -- in TypeSpecification
MachineCode I -- in TypeSpecification
[ Expression ] I -- for
STRING initialization
CODE -- for SIGNAL initialization




 empty I 4- InitExpr = InitExpr
empty I 4- InitExpr = InitExpr
FOR identifier Direction IN LoopRange empty I Repetition I Iteration I Assignation identifier : Extractltem
KeywordExtract
KeywordExtractList
, KeywordExtract
identifier
Label
I LabelList , Label
Expression
LOOP
IterativeControl
ConditionTest
ExitSeries
I ExitSeries ; I FinishedExit I ExitSeries ; FinishedExit empty I REPEAT LoopExits
Su
brangeTC I Typeldentifier I BOOLEAN I CHARACTER
LoopControl
DO
OpenClause
DeclarationSeries EnableClause
StatementSeries LoopExitsClause ENDLOOP
 NOTIFY Variable I BROADCAST Variable
NOTIFY Variable I BROADCAST Variable
NULL
empty
I OPEN OpenList ;
Expression I identifier : Expression Openitem I OpenList , Openitem empty I [ I CatchSe ries ]
Extractltem
I
PositionalExtractList
, Extractltem
THROUGH Su b range -- in
Expression
RESTART
Variable OptCatchPhrase -- Variable in Expression
RESUME I
RESUME [ ComponentList ComponentList in Expression
RETRY RETURN
I
 RETURN [ ComponentList ] ComponentList in Expression
RETURN [ ComponentList ] ComponentList in Expression
RETURN WITH ERROR
Call
 Select I SelectVariant
Select I SelectVariant
SELECT Leftltem FROM StmtChoiceSe
ries
ENDCASE FinalStmtChoice
WITH Openitem SELECT Tagltern FROM ChoiceSe ries
ENDCASE
FinalStmtChoice
SIGNAL Call I ErrorCall START Call
empty I Statement I Statement ; StatementSeries
TestList => Statement ; I StmtChoiceSeries TestList =>
Statement ;
STOP OptCatchPhrase
empty I Expression
Expression I RelationTail --RelationTail
in Expression
Test
I TestList , Test
 WAIT Variable
OptCatchPhrase
WAIT Variable
OptCatchPhrase
· . . •
AssignmentExpr I Disjunction I
ForkCall I IfExpr JoinCall I NewExpr I SelectExpr I
SignalCall I --SignalCall
in Statement
StartCall --StartCall
in Statement
 +
—
+
—
LeftSide
RightSide
MIN [ ExpressionList ] I MAX [
ExpressionList ] I ABS [ Expression ] LENGTH [ Expression ] I BASE [ Expression ]
TypeOp [ TypeSpecification ] I
DESCRIPTOR [ Expression ]
DESCRIPTOR
[ Expression , Expression ] I

 DESCRIPTOR [ Expression , Expression ,
TypeSpecification ] AdjectiveList => Expression , I AdjectiveList
in Statement
DESCRIPTOR [ Expression , Expression ,
TypeSpecification ] AdjectiveList => Expression , I AdjectiveList
in Statement
ChoiceList AdjectiveList => Expression ,
empty I Expression I NULL
KeywordComponentList
I PositionalComponentList Negation I Conjunction AND Negation
OptionalTypeld [ ComponentList ]
Conjunction
I Disjunction OR Conjunction
TestList => Expression , TestList
in Statement
ExprChoiceList
TestList => Expression ,
 Expression I ExpressionList , Expression — Primary I
Primary
Expression I ExpressionList , Expression — Primary I
Primary
FORK Call
BuiltinCall I Call --
Call in Statement
IF Expression THEN Expression ELSE
Expression
(
Expression ) [ Expression ] I Variable [ Expression ] ( Expression ) t
I Variable t
JOIN Call
identifier :
Component
KeywordComponentList
= KeywordComponent
KeywordComponentList,
KeywordComponent
y LeftSide =
Literal =
-) MultiplyingOp =
·
Negation =
-
NewExpr =
· Not =
OptionalTypeld =
identifier I Call I --
Call in Statement
IndexedAccess I
QualifiedAccess I IndirectAccess I LOOPHOLE [ Expression ]
LOOPHOLE
[ Expression , TypeSpecification
numericLiteral I -- all defined
outside the grammar
stringLiteral I
characterLiteral
*I/ IMOD
Relation I Not
Relation
NEW Variable
OptCatchPhrase
- I NOT
empty
I Typeldentifier -- in
TypeSpecification
c
PositionalComponentList = Component I
PositionalComponentList
, Component
|
ü
|
Primary
|
=
|
Variable I Literal I ( Expression) FunctionCall
I
|
|
|
|
|
Constructor I ALL [ Expression ] @ LeftSide I identifier [
Expression ]
|
|
|
Product
|
=
|
Factor I Product MultiplyingOp
Factor
|
|
V
|
QualifiedAccess
|
=
|
( Expression ) . identifier I Variable .
identifier
|
|
co
|
Relation
|
=
|
Sum I Sum RelationTail
|
|
0
|
RelationalOp
|
=
|
# I = I < I <= I>
I>=
|
|
|
RelationTail
|
=
|
RelationalOp Sum I Not
RelationalOp Sum I
|
|
|
|
|
IN SubRange I Not IN Subrange
|
|
|
RightSide
|
=
|
Expression.
|
|
|
SelectExpr
|
=
|
SelectExprSimple SelectExprVariant
|
|
|
SelectExprSimple
|
=
|
SELECT Leftltem FROM Leftltem in Statement
|
|
|
|
|
ExprChoiceList
|
|
|
|
|
ENDCASE => Expression
|
|
|
SelectExprVariant ::=
|
WITH Openitem SELECT Tagltem FROM Openitem, Tagltem in Statement
|
|
|
|
|
ChoiceList
|
|
|
|
|
ENDCASE => Expression
|
|
ü
|
Subrange
|
=
|
Sub rangeTC I -- in TypeSpecification
|
|
|
|
|
Typeldentifier -- in TypeSpecification
|
|
C)
|
Sum
|
=
|
Product I Sum AddingOp Product
|
|
|
TypeOp
|
=
|
SIZE I FIRST I LAST
|
|
v
|
Variable
|
=
|
LeftSide
|
INDEX
In
this index, bold face page numbers
indicate where the primary, defining
information can be found: plain page
numbers designate further examples.
! 137.
138, 140
" 83
9
* 12, 94, 95
+ 12
- 12
2, 5, 6
34, 104, 106-7
/ 12
2
; 5-6, 53, 57, 136, 137
=> 54,
56, 94. 96, 136, 138, 140
@ 29, 42, 44, 147
11 125,
130
t 42
5, 17, 63, 76,130 ABS 5,12
Access 94, 104, 117-20
activation 72.137
actual procedure 68, 74. 78
actual
tag 94, 97, 99
AddingOperator 12
adjective 96
adjectives 92, 97
aggregate
type 22
aligned 29, 42,
69
ALL 30
AlternateName 60, 98
ANY 136,
138-9
argument 72, 72
arguments 67, 144
arguments
buffered 150
array 22,
27-8
constructor 28,
30
descriptor 85, 87
ARRAY 27-8,
29
Assignation 63, 63
assignment 6, 51
expression 52
AssignmentExpr 11, 17
AssignmentStmt 7, 51
automatic
dereferencing 44
B 8
balancing 45, 47
BASE 29, 41, 43-4,
86, 87, 88, 90-1
base type 25
BCD 103,
123
BEGIN 57, 136
Binary Configuration Description 103,123
binding 101, 103. 123-4. 132
blank 6
block 57
Block 57,57,73,137,140
BNF 2
BOOLEAN 7-8, 16, 22, 24, 53
bound
variant 97
bound
variant type 93, 95, 96
bounds 64
BROADCAST 159, 160-1
BuildinCall 12, 12
built-in type 7
C 9
C/Mesa 103,
120, 125
call 67
Call 12, 71,137, 140
CallStmt 71
CARDINAL 7, 7, 10, 22. 26-7,
49
Catch 134,
136, 137-9
catch
phrase 136, 139,
150, 154
CHARACTER 7, 9, 15, 22
characterLiteral 9
client 120
module 123
CODE 125, 135, 141
coercion 46. 73
colon 6
comma 56, 94
comment 5, 6
common part 92
CommonPart 118
compatible 70
compilation
order 110
CompilationUnit 104
compile-time 84, 104, 105
constant 18, 30,
53
completely bound variant 100
component 27, 31, 125
component type 27
components 97
ComponentType 29
COMPUTED 94,
100
computed tag 93, 95, 97,100
CONDITION 155, 158, 161
condition
variable 155
ConditionTest 62, 63
configuration 123
Configuration 125
CONFIGURATION 125, 126
Configuration Description 103,
123-4
configuration
prototype 125
conform 7, 10, 72
conforming 69
Conjunction 16
CONNECT 146,
147, 150
constant 18
constructed data type 20
constructor 35. 93
Constructor 30.35
CONTINUE 140,
141, 146, 150
CONTROL 103,
125
control fault 149
link 148
transfer 148
variable 64
ControlVariable 63, 63
coroutine 144
covering condition variable 160
CR 6,141
D 8
Debugger 136, 139
declaration 68
Declaration 19
DeclarationSeries 57
DECREASING 63-4
default Access 120
default field 112
default field
values 36
default-named
interfaces 127-8
DefaultOption 37
DefaultSpecification 37
defining occurance 108
DEFINITIONS 78,
104,105-6, 110, 117, 120
definitions module 101
DESCRIPTOR 29,
85-6. 87, 91
detached process 154
determination of
representation 49
Digit 2
DIRECTORY 78, 104-5, 106, 126
discrimination 98, 100
Disjunction 11, 16
DO 5,
62, 136
element type 22
ElementType 22,
25
elided 30
elided component 35
elides 36
ELSE 5,52,76
empty 3,
30
empty
constructor 72
extractor 39
interval 16,
29ENABLE 137, 138, 140-1
EnableClause 57
END 57,
76
ENDCASE 54.56,77,94,99
ENDLOOP 5.62,64
ENTRY 155,156
entry procedure 155
enumerated
type 22
enumeration 21, 94
equality 6
equivalent 10
ERROR 135.136,141.149
ERROR, unnamed 136
ErrorCall 135
exceptional conditions 134
EXIT - 65,
66, 139, 141
ExitsClause 57, 57, 137
expansion 80
explicit
component 35
naming 126-7
qualification 109
export 102, 117,126
record 102
EXPORTS 78,
103-4, 117, 121, 124-5, 126,
127
Expression 11, 51
ExpressionList 12
external
procedure 157
extractor 38. 128
Extractor 51
Factor 12
FALSE 8,
24
FaultHandler 150, 151
field
list 32
FieldDescription 118
FieldList 31,
32
FINISHED 65,
66, 141
FIRST 24,
26
floating-point 10
fonts 1
FOR 63,
64
forcible
termination 65, 66
FORK 136,
152-3. 153, 154
formation
rules 2
frame 57, 148
FRAME 104, 116, 125, 132, 146
free
conformance 48, 70
 FROM 104. 146
FROM 104. 146
FunctionCall 12
fundamental
operation GCD 4
GlobalAccess 117,120
GOTO 57.
58-9. 64, 66. 139
home
module 117
identifier 21
constant 23. 94
list 6
identifier 5, 127
IdList 3.6
IF 5.
52.76
expression 53
statement 52
lfStmt 52
implementing 121
implementor 120
implicit
qualification 99
import 101
imports 126
IMPORTS 78,102-4,
115, 124-5, 126, 127
IN 15,
47, 55, 63
include 105
IncludeList 104
indefinite index type 86
index
type 2'7
indexed
reference 27
IndexedReference 29
IndexType 29.85
inequality 6
inherent
representation 49
type 45
initialization 18,
68, 84, 135
Initialization 19, 33
inline 69, 73, 80
INLINE 80,
113-4
InlineOption 73
instance 115, 124
INTEGER 7. 7, 10, 22, 26-7, 49
interface 101, 120. 125, 135, 158
element 110
record 115, 116,127
type 115, 116
variable 110. 111-2, 113-4
INTERNAL 157,
165
internal procedure 158
interval 15, 63
Interval 15
Iteration 63, 63
Ite rativeControl 63
JOIN 136,
152-3, 153, 154
jump
table 55
keyword 39
constructor 31,
35, 35, 74
extractor 74
name 35
Label 58
Labels 58
LAST 24,
26
LeftSide 7, 29, 38. 42. 45. 51
length 82
LENGTH 29.
86. 87
lengthening 43
lexical units 6
link 124
LinkageFault 148,
149, 150
LINKS 125,
125
literal 18
Literal 12
loader 132
loading 123
local string literal 84
local variable 68
LOCK 161
LOCKS 162,
164, 166
LocksClause 162, 165
LONG 14,
43, 87, 92
CARDINAL 7,
9-10
INTEGER 7,
9-10
POINTER 43
STRING 85
long numeric type 9
LOOP 65,
139
loop control 61
loop statement 61
LoopCloseStatement 65
LoopCont rol 62
LoopExitsClause 64
LOOPHOLE 47
LoopRange 63,
64
lower bound 16
lower-case 5
MACHINE DEPENDENT 33, 94, 95, 166
MACHINE DEPENDENT
RECORD 29
MAX 12,
47
maxlength 82, 83
MIN 12,
47
MOD 5
module 61, 68, 101
ModuleBody 104
monitor 154, 155
initialization 168
lock 155
MONITOR 156,
162
MONITORED RECORD 162,
163-4
MONITORLOCK 156,
162, 166
Multi-module monitor 163
multiple statements 6
MultiplyingOperator 12
name reference 108
name scope 34. 108
NamedFieldList 32, 118
Negation 16
nested
configurations 130
procedure 78
signals 142
NEW 116,
131-2. 136, 146
Next-Statement 51, 55.
62
NIL 43,
44, 76
non-interface
element 110
type 101
non-local
variable 68
non-privileged 117
NOTIFY 155,
157, 159, 160-1
NULL 56, 94
number 8
numeric
literal 8
operators 12
type 7, 26
object
file 103
module 101
Object monitor 165
objects 165
OctalDigit 2
omission 36
OPEN 59,106, 108-9
open
clause 98,
107
item 99
OpenClause 57, 61
operator 12
precedence 17
ORDERED 41,43
ordered
type 22
OVERLAID 94,
100. 148
overlaid tag 95
PACK 125
packed 69
PACKED 29,
85, 87
parameter 67,134
record 67
pending 147,149-50
phrase
class 2
PLUS 125.
130
pointer 22. 39
arithmetic 43
POINTER 41,43-4,88
POINTER
TO FRAME 104, 116
PORT 144-5,
146, 148, 151
port-compatible 148
PortFault 147, 149, 150
positional constructor 35, 36
precedence 12, 52, 54
PredefinedType 19
Primary 12
PRIVATE 104,
112-3, 117-20
privileged 117
procedure 67
body 68
calls 71
descriptor 148
type 69
value 70, 148
variable 74,
110
PROCEDURE 69,
76, 148
Procedu
reBody 73
process 166
PROCESS 153, 153
Product 12
PROGRAM 104,
115, 117. 120, 132, 145-6
program 101
prototype 116,
125
variable 116
PUBLIC 76.
103-4, 113, 117, 117, 118-9, 121
qualification 34, 60, 106
qualified reference 31,
108
qualifier 74
Queue 156
range
assertion 27
error 25
readonly 40
READONLY 41,
111
REAL 7,
10, 10, 46
recompiling 109
record 31
constructor 31,
35
single-component 73
RECORD 32, 76, 94, 95
recursive 72
substitution 3
reentrant 72
reference type 39
Reject 139
relational
operators 15
RELATIVE 43, 88, 90-1
relative
array descriptor 89,
91.2
pointer 88,
89
relocation 88
REPEAT 64,
141
Repetition 63
reserved
words 2, 5
RESPONDING 145,
151
RESTART 116, 132.3,
136, 146-7, 150
result 67. 135, 144
record 73
Resume 139
RESUME 136, 136, 138. 140,
141
ResumeF.rror 141
RETRY 140. 141
RETURN 69,72,74.132.136,148
return
link 138, 149
RETURN WITH ERROR 135,
138. 139, 166-7
RETURNS 69, 76
RightSide 7. 51
scalar
type 22
scale
factor 8
scope 74,
79, 99, 108, 137
SELECT 54,54,56.77.93-6,98,99-100,141,
148
SELECT expressions 56
SelectExpr 56
SelectStmt 54
self-contained 124
Series 3
SHARES 104, 117,120
short numeric type 9
SIGNAL 59.135, 136, 141
SignalCall 135
Signaller 138,
139, 142, 150
signals 134
actual 135
catching 138
nested 142
signed number 7
single-component
record 73
SIZE 34, 76
SP 141
space 6
START 83, 116, 124, 132, 133, 136,
138, 144,
146-7
start trap 111,
133, 147
startup
transient 144, 147
statement 51
Statement 51
StatementSeries 57
static variable 124
StmtSeries 3
STOP 124, 132-3, 136
STRING 7, 82, 83
string literal 83
StringBody 82, 87
strongly
typed 4
subrange 21
type 22.
24
Sum 12
syntax notation 2
TAR 6.
141
tag 93
Tag 118
target
representation 49
type 45
TC 21
terminate
conditionally 62
forcibly 65
normally 63
text 82
THEN 5,52,76,125,130
THROUGH 63
time stamp 109
timeout 161
TRUE 8, 24
TYPE 20, 21
type
constructor 7
conversion 46
determination 45
type-correct 45
TypeConstructor 21
TypeDecla ration 20
Typeldentifier 21,
96,
107
TypeSpecification 21, 90
unbound variant 93
unique type 91
UnnamedFieldList 31
unqualified 61
unsigned number 7, 43
UNSPECIFIED 19, 43
UNTIL 5, 62. 140
Unwind 139
UNWIND 139, 140, 149-50,
167
upper bound 16
upper-case 5
user-defined type 7
USING 78, 106, 109,
162, 165-6
Variable 12
variant
part 92,
93, 97. 148
record 92
VariantFieldList 118
VariantPart 118
virtual interface record 102
voided component 35
voids 36
WAIT 136, 155, 157, 159,
160-1, 166, 168
WHILE 62
WITH 98
WORD 19
XFER 148


|
|
r
J
|
C‑
-'\10(.:!1"-i h^f,01.,r
tilAQ* -"7.1
rpcf,
![]() CHAPTER 2. BASIC DATA TYPES AND EXPRESSIONS
CHAPTER 2. BASIC DATA TYPES AND EXPRESSIONS lowerCaseA
lowerCaseA 














![Text Box: = RECORD[c: CTjpe]:](23a-MesaManualOCR_files/image037.gif)

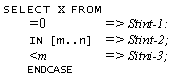



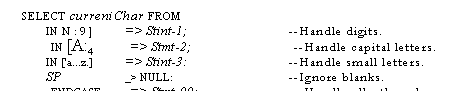




![Text Box: PriniLexicon: PUBLIC PROCEDURE = BEGIN PrMtNode[root] END:](23a-MesaManualOCR_files/image068.gif)
![Text Box: PrintAlode: PROCEDURE[n: NodePtr] =- BEGIN
IF n = NIL THEN RETURN;
PrintNode[ialink];
10Defs.WriteLine[n.string]; PrintNode[n.rlink];
END; END.](23a-MesaManualOCR_files/image069.gif)
![Text Box: lexRecFA 4- LexiconFA[]; lexRecP F LexiconP[];
lexRec lexRecFA PLUS lexRecP; LexiconClient[I0Deft lexRec];](23a-MesaManualOCR_files/image070.gif)


![Text Box: For =7
4-
n: T ?afield
P1'
gx [a.. b] [a.. b) (a..b] (a.b)
FOR i I. k f[x, y, z]](23a-MesaManualOCR_files/image073.gif)
















![Text Box: LeftSide 4- RightSide I LeftSide, RightSide in Expression
Extractor f RightSide
BEGIN
OpenClause
EnableClause
DeclarationSeries StatementSeries ExitsClause
END
Variable I -- in Expression
Variable [ ComponentList ComponentList in Expression
Variable [ ComponentList CatchSeries
Variable [ ! CatchSeries]
ExpressionList => Statement ExpressionList in Expression
Catch I ANY => Statement
Catchltem I Catch ; CatchSeries
AdjectiveList => Statement :1 ChoiceSeries AdjectiveList => Statement ;
BEGIN
Body
ExitsClause END
empty I WHILE Expression I UNTIL Expression CONTINUE
IdList :
Access -- Access in TypeSpecification
ReadOnlyOption EntryOption ReadOnlyOption in TypeSpecification
TypeSpecification
Initialization ; I
IdList : Access TYPE = Access TypeSpecification ;
empty I DeclarationSeries Declaration empty I DECREASING
empty I ELSE Statement
ENABLE Catchltem ; I
ENABLE BEGIN CatchSeries END ;](23a-MesaManualOCR_files/image114.gif)