Butler W. Lampson and Howard E. Sturgis

June 1, 1979

Citation: Crash recovery in a distributed data storage system. Unpublished technical report, Xerox Palo Alto Research Center, June, 1979, 25 pp.

Links: Abstract, Postscript, Acrobat, Word.

Email: blampson@microsoft.com. This paper is at http://www.research.microsoft.com.

This paper was circulated in several drafts, but it was never published. Much of the material appeared in Distributed Systems—Architecture and Implementation, ed. Lampson, Paul, and Siegert, Lecture Notes in Computer Science 105, Springer, 1981, pp 246-265 and pp 357-370.

An algorithm is described which guarantees reliable storage of data in a distributed system, even when different portions of the data base, stored on separate machines, are updated as part of a single transaction. The algorithm is implemented by a hierarchy of rather simple abstractions, and it works properly regardless of crashes of the client or servers. Some care is taken to state precisely the assumptions about the physical components of the system (storage, processors and communication).

atomic, communication, consistency, data base, distributed computing, fault tolerance, operating system, recovery, reliability, transaction, update.

We consider the problem of crash recovery in a data storage system that is constructed from a number of independent computers. The portion of the system that is running on some individual computer may crash, and then be restarted by some crash recovery procedure. This may result in the loss of some information that was present just before the crash. The loss of this information may, in turn, lead to an inconsistent state for the information permanently stored in the system.

For example, a client program may use this data storage system to store balances in an accounting system. Suppose that there are two accounts, called A and B, which contain $10 and $15 respectively. Further, suppose the client wishes to move $5 from A to B.

The client might proceed as follows:

Now consider a possible effect of a crash of the system program running on the machine to which these commands are addressed. The crash could occur after one of the write commands has been carried out, but before the other has been initiated. Moreover, recovery from the crash could result in never executing the other write command. In this case, account A is left containing $5 and account B with $15, an unintended result. The contents of the two accounts are inconsistent.

There are other ways in which this problem can arise: accounts A and B are stored on two different machines and one of these machines crashes; or, the client itself crashes after issuing one write command and before issuing the other.

In this paper we present an algorithm for maintaining the consistency of a file system in the presence of these possible errors. We begin, in section 2, by describing the kind of system to which the algorithm is intended to apply. In section 3 we introduce the concept of an atomic transaction. We argue that if a system provides atomic transactions, and the client program uses them correctly, then the stored data will remain consistent.

The remainder of the paper is devoted to describing an algorithm for obtaining atomic transactions. Any correctness argument for this (or any other) algorithm necessarily depends on a formal model of the physical components of the system. Such models are quite simple for correctly functioning devices. Since we are interested in recovering from malfunctions, however, our models must be more complex. Section 4 gives models for storage, processors, and communication, and discusses the meaning of a formal model for a physical device.

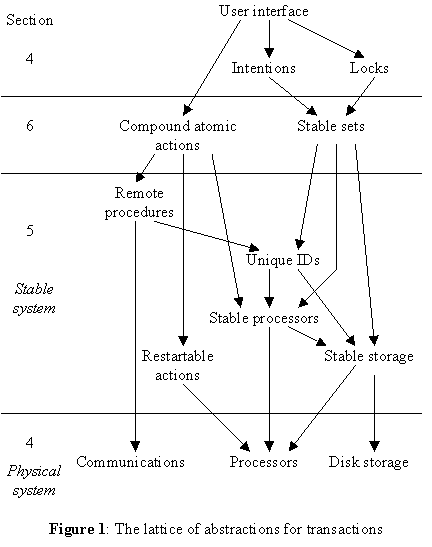
Starting from this base, we build up the lattice of abstractions shown in figure 1. The second level of this lattice constructs better behaved devices from the physical ones, by eliminating storage failures and eliminating communication entirely (section 5). The third level consists of a more powerful primitive that works properly in spite of crashes (section 6). Finally, the highest level constructs atomic transactions (section 7). Parallel to the lattice of abstractions is a sequence of methods for constructing compound actions with various desirable properties. A final section discusses some efficiency and implementation considerations. Throughout we give informal arguments for the correctness of the various algorithms.

Our data storage system is constructed from a number of computers; the basic service provided by such a system is reading and writing of data bytes stored in the system and identified by integer addresses. There are a number of computers that contain client programs (clients), and a number of computers that contain the system (servers); for simplicity we assume that client and server machines are disjoint. Each server has one or more attached storage devices, such as magnetic disks. Some facility is provided for transmitting messages from one machine to another. A client will issue each read or write command as a message sent directly to the server storing the addressed data, so that transfers can proceed with as much concurrency as possible.

We follow tradition in using a pair of integers <f, b> to address a byte, where f identifies the file containing the byte, and b identifies the byte within the file. A file is thus a sequence of bytes addressed by integers in the range 1..n, where n is the length of the file. There are two commands available for accessing files: a generalized Read command, and a generalized Write command. The generality allows information associated with a file other than its data bytes to be read and written, for example its length, or protection information associated with the file; these complications are irrelevant to our subject and will not be mentioned again. A client requests the execution of a command by sending a message containing the command to the appropriate server. When the command has been completed, the server sends a message to the client containing a response. In the case of a read command, this response will contain the requested data. For a write command, the response is simply an acknowledgement. It is necessary to provide interlocks between the concurrent accesses of different clients.

It should now be clear that our distributed data storage system is not a distributed data base system. Instead, we have isolated the fundamental facilities required by a data base system, or any other system requiring long-term storage of information: randomly addressable storage of bits, and arbitrarily large updates which are atomic in spite of crashes and concurrent accesses. We claim that this is a logically sound foundation for a data base system: if it proves to be unsatisfactory, the problem will be inadequate performance.

For any system, we say that a given state is consistent if it satisfies some predicate called the invariant of the system. For example, an invariant for an accounting system might be that assets and liabilities sum to zero. The choice of invariant obviously depends on the application, and is beyond the scope of a data storage system. The task of the storage system is to provide facilities which, when properly used, make it possible for a client application program to maintain its invariant in spite of crashes and concurrent accesses.

A suitable form for such facilities is suggested by the following observation. Any computation which takes a system from one state to another can be put into the form

where F is a function without side effects. A state is a function that assigns a value to each element (called an address) in some set (called an address space). In general F will change only the values at some subset of the addresses, called the output set of F; these new values will depend only on the values at some other subset of the addresses, called the input set.

That is, the function needs to read only those addresses whose values are actually referenced by the computation, and the assignment needs to write only those addresses whose values are actually changed by the computation. Such a computation will clearly be atomic in the presence of crashes if the assignment is atomic in the presence of crashes, that is, if either all the writes are done, or none of them are. Two such computations F and G may run concurrently and still be atomic (that is, serializable) if the input set of F is disjoint from the output set of G, and vice versa.

In pursuit of this idea, we introduce the notion of a transaction (the same concept is used in [1], and elsewhere in the data base literature, to define consistency among multiple users of a common data base). A transaction is a sequence of read and write commands sent by a client to the file system. The write commands may depend on the results of previous read commands in the same transaction. The system guarantees that after recovery from a system crash, for each transaction, either all of the write commands will have been executed, or none will have been. In addition, transactions appear indivisible with respect to other transactions that may be executing concurrently; that is, there exists some serial order of execution which would give the same results. We call this the atomic property for transactions. The client will indicate the commands of a transaction by surrounding them with Begin and End commands. If the client fails to issue the end transaction command (perhaps because he crashes), then a time out mechanism will eventually abort the transaction without executing any of the write commands.

Assuming this atomic property for transactions, consider how the previous example might be implemented by a client. The client first issues a Begin command, and then continues just as in the example in section 1. After sending the two write commands, he sends End. This transaction moves $5 from A to B. Notice that the client waits for the responses to the read commands, then computes the new balances, and finally issues write commands containing the new balances.

A client may decide to terminate a transaction before it is completed. For this purpose we have an additional command, Abort. This terminates the transaction, and no write commands issued in the transaction will take effect. Because the system also times out transactions, the Abort command is logically unnecessary, but the action it causes also occurs on a timeout and hence must be implemented in the system.

Thus, we have two groups of commands, which constitute the entire interface between the data storage system and its clients:

• Data commands: Read, Write
• Control commands: Begin, End, Abort

We shall return to transactions in section 7 after laying some necessary groundwork.

To show the correctness of our algorithms in spite of imperfect disk storage, processor failures (crashes), and unreliable communication, we must have a formal model of these devices. Given this model, a proof can be carried out with any desired degree of formality (quite low in this paper). The validity of the model itself, however, cannot be established by proof, since a physical system does not have formal properties, and hence its relation to a formal system cannot be formally shown. The best we can do is to claim that the model represents all the events that can occur in the physical system. The correctness of this claim can only be established by experience.

In order to make our assumptions about possible failures more explicit, and we hope more convincing, we divide the events which occur in the model into two categories: desired and undesired: in an fault-free system only desired events will occur. Undesired events are subdivided into expected ones, called errors, and unexpected ones, called disasters. Our algorithms are designed to work in the presence of any number of errors, and no disasters: we make no claims about their behavior if a disaster occurs.

In fact, of course, disasters are included in the model precisely because we can envision the possibility of their occurring. Since our system may fail if a disaster does occur, we need to estimate the probability p that a disaster will occur during an interval of operation To; p is then an upper bound on the probability that the system will fail during To. The value of p can only be estimated by an exhaustive enumeration of possible failure mechanisms. Whether a given p is small enough depends on the needs of the application.

In constructing our model, we have tried to represent as an error, rather than a disaster, any event with a significant probability of occurring in a system properly constructed from current hardware. We believe that such a system will have very small p for intervals To of years or decades. The reader must make his own judgment about the truth of this claim.

Our general theme is that, while an error may occur, it will be detected and dealt with before it causes incorrect behavior. In the remainder of this section, we present our model for the three main physical components on which the system depends: disk storage, processors, and communication. In the next section, we describe how errors are handled: in general this is done by constructing higher-level abstractions for which desired events are the only expected ones.

Our model for disk storage is a set of addressable pages, where each page contains a status (good, bad) and a block of data. There are two actions by which a processor can communicate with the disk:

procedure Put(at: Address, data: Dblock)

procedure Get(at: Address) returns (status: (good, looksBad), data: Dblock)

Put does not return status, because things which go wrong when writing on the disk are usually not detected by current hardware, which lacks read-after-write capability. The extension to a model in which a Put can return bad status is trivial.

We consider two kinds of events: those that are the result of the processor actions Get and Put, and those that are spontaneous.

The results of a Get(at: a) are:

The definition of a persistent read error implies that if TR successive Gets of a good page have all returned looksBad, the page must actually be bad (that is, has decayed or been badly written; see below), or else a disaster has happened, namely the persistent error. This somewhat curious definition reflects the fact that the system must treat the page as bad if it cannot be read after repeated attempts, even though its actual status is not observable.

The effects of a Put(at: a, data: a) are:

The remaining undesired events, called decays, model various kinds of accidents. To describe them we need some preliminaries. Each decay event will damage some set of pages, which are contained in some larger set of pages which is characteristic of the decay. For example, a decay may damage many pages on one cylinder, but no pages on other cylinders; or many pages on one surface, but no pages on other surfaces. We call these characteristic sets decay sets; they are not necessarily disjoint, as the example illustrates. Two pages are decay related if there is some decay set which contains both. We also assume a partitioning of the disk pages into units (such as disk drives), and a time interval TD called the unit decay time. We assume that any decay set is wholly contained in one unit, and that it is possible to partition each unit into pairs of pages that are not decay-related (in order to construct stable storage; see 5.1). TD must be very long compared to the time required to read all the disk pages.

A decay is a spontaneous event in which some set of pages, all within some one characteristic decay set, changes from good to bad. We now consider the following spontaneous events:

Other events may be obtained as combinations of these events. For example, a Put changing the wrong page can be modeled as a Put in which the addressed page is unchanged (error), and an undetected error in which some other page spontaneously changes to a new good value (disaster). Similarly, a Put writing the wrong data can be modeled in the same way, except that the written page is the one that suffers the undetected error. One consequence of this model is that writing correct data at the wrong address is a disaster and hence cannot be tolerated.

Our model for a processor is conventional except for the treatment of crashes. A processor consists of a collection of processes and some shared state. Each process is an automaton with some local state, and makes state transitions (executes instructions) at some finite non-zero rate. Instructions can read and write the shared state as well as the local state of the process: some standard kind of synchronization primitive, such as monitors, allows this to be done in an orderly way. For simplicity we consider the number of processes to be fixed, but since a process may enter an idle state in which it is simply waiting to be reinitialized, our model is equivalent to one with a varying but bounded number of processes. One of the processes provides an interval timer suitable for measuring decay times (see 4.1 and 5.1). The union of the shared state and the process states is the state of the processor. A processor can also interact with the disk storage and the communication system as described in sections 4.1 and 4.3.

A crash is an error that causes the state of the processor to be reset to some standard value; because of this effect, the processor state is called volatile state. This implies that the processor retains no memory of what was happening at the time of the crash. Of course the disk storage, or other processors that do not crash, may retain such memory. In a system with interesting long-term behavior, such as ours, a processor recovering from a crash will examine its disk storage and communicate with other processors in order to reach a state that is an acceptable approximation to its state before the crash. Since a crash is expected, it may occur at any time; hence a crash may occur during crash recovery, another crash may occur during recovery from that crash, and so forth.

Our model includes no errors in the processor other than crashes. The assumption is that any malfunction will be detected (by some kind of consistency checking) and converted into a crash before it affects the disk storage or communication system. It may well be questioned whether this assumption is realistic.

Our model for communication is a set of messages, where each message contains a status (good, bad), a block of data, and a destination which is a processor. Since we are not concerned with authentication in this paper, we assume that the source of a message, if it is needed, will be encoded in the data. There are two actions by which a processor can communicate with another one:

The similarity to the actions for disk storage is not accidental. Because messages are not permanent objects, however, the undesired events are somewhat simpler to describe. The possible events are as follows:

The possible results of a Receive executed by processor p are:

There may be an arbitrary delay before a Receive returns.

The effects of a Send(to: q, data: d) are:

Finally, we consider the following spontaneous events:

As with disk storage, other undesired events can be obtained as combinations including these spontaneous events.

Throughout this paper we shall be discussing program fragments which are designed to implement the actions (also called operations or procedures) of various abstractions. These actions will usually be compound, that is, composed from several simpler actions, and it is our task to show that the compound action can be treated at the next higher level of abstraction as though it were simple. We would like a simple action to be atomic. An atomic action has both of the following properties:

• Unitary: If the action returns (that is, the next action in the program starts to execute), then the action was carried out completely; and if the system crashes before the action returns, then after the crash the action has either been carried out completely, or (apparently) not started.
• Serializable: When a collection of several actions is carried out by concurrent processes, the result is always as if the individual actions were carried out one at a time in some order. Moreover, if some process invokes two actions in turn, the first completing before the second is started, then the effect of those actions must be as if they were carried out in that order.

Unfortunately, we are unable to make all the actions in our various abstractions atomic. Instead, we are forced to state more complicated weak properties for some of our compound actions.

Consider the effect of crashes on a compound action S. The unitary property can be restated more formally as follows: associated with S is a precondition P and a postcondition Q. If P holds before S, and if S returns, then Q will hold; if a crash intervenes, then (P Ú Q) will hold. P and Q completely characterize the behavior of S.

The behavior of any action S in the presence of crashes can be characterized by a precondition P and two postconditions QOK and Qcrash If P holds before S and S returns, then QOK holds. On the other hand, if there is a crash before S returns, then Qcrash holds. Sometimes we mean that Qcrash holds at the moment of the crash, and sometimes that it holds after the lower levels of abstraction have done their crash recovery. Notice that since a crash can occur at any moment, and in particular just before S returns, QOK must imply Qcrash Notice also that the unitary property is equivalent to asserting that Qcrash = (P Ú QOK)

During crash recovery it is usually impossible to discover whether a particular action has completed or not. Thus, we will frequently require that S be restartable, by which we mean that Qcrash implies P (hence QOK implies P). If S is restartable and S was in progress at the moment of the crash, then S can be repeated during crash recovery with no ill effects. Notice that atomic does not imply restartable.

Section 5.4 deals with weak properties of compound actions that are substitutes for serializability.

The physical devices described in the previous section are an unsatisfactory basis for the direct construction of systems. Their behavior is uncomfortably complex; hence there are too many cases to be considered whenever an action is invoked. In this section we describe how to construct on top of these devices a more satisfactory set of virtual devices, with fewer undesired properties and more convenient interfaces. By eliminating all the errors, we are able to convert disk storage into an ideal device for recording state, called stable storage. Likewise, we are able to convert communications into an ideal device for invoking procedures on a remote processor. By "ideal" in both cases we mean that with these devices our system behaves just like a conventional error-free single-processor system, except for the complications introduced by crashes.

We have not been so successful in concealing the undesired behavior of processors. In fact, the remaining sections of the paper are devoted to an explanation of how to deal with crashes. The methods for doing this rely on some idealizations of the physical processor, described in section 5.2.

The disk storage not used as volatile storage for processor state (see 5.2) is converted into stable storage with the same actions as disk storage, but with the property that no errors can occur. Since the only desired events are ideal reads and writes, stable storage is an ideal storage medium, with no failure modes which must be dealt with by its clients.

To construct stable storage, we introduce two successive abstractions, each of which eliminates two of the errors associated with disk storage. The first is called careful disk storage; its state and actions are specified exactly like those of disk storage, except that the only errors are a bad write immediately followed by a crash, and infrequent decay. A careful page is represented by a disk page. CarefulGet repeatedly does Get until it gets a good status, or until it has tried n times, where n is the bound on the number of soft read errors. This eliminates soft read errors. CarefulPut repeatedly does Put followed by Get until the Get returns good with the data being written. This eliminates null writes; it also eliminates bad writes, provided there is no crash during the CarefulPut. More precisely, QOK for CarefulPut is the desired result, but Qcrash is not. Since crashes are expected, this isn’t much use by itself.

A more complicated construction is needed for stable storage. A stable page consists simply of a block of data, without any status (because the status is always good). In addition to Get and Put, it has a third action called Cleanup. It is represented by an ordered pair of careful disk pages, chosen from the same unit but not decay-related. The definition of units ensures that this is possible, and that we can use all the pages of a unit for stable pages. The value of the data is the data of the first representing page if that page is good, otherwise the data of the second page. The representing pages are protected by a monitor that ensures that only one action can be in progress at a time. Since the monitor lock is held in volatile storage and hence is released by a crash, some care must be taken in analyzing what happens when there is a crash during an update operation.

We maintain the following invariant on the representing pages: not more than one of them is bad, and if both are good they both have the data written by the most recent StablePut, except during a StablePut action. The second clause must be qualified a little: if a crash occurs during a StablePut, the data may remain different until the end of the subsequent crash recovery, but thereafter both pages’ data will be either the data from that StablePut or from the previous one. Given this invariant, it is clear that only the desired events and the unexpected disasters for disk pages are possible for stable pages.

Another way of saying this is that StablePut is an atomic operation: it either changes the page to the desired new value, or it does nothing and a crash occurs. Furthermore, decay is unexpected.

The actions are implemented as follows. A StableGet does a CarefulGet from one of the representing pages, and if the result is bad does a CarefulGet from the other one. A StablePut does a CarefulPut to each of the representing pages in turn; the second CarefulPut must not be started until the first is complete. Since a crash during the first CarefulPut will prevent the second one from being started, we can be sure that if the second CarefulPut is started, there was no write error in the first one.

The third action, called Cleanup, works like this:

This action is applied to every stable page before normal operation of the system begins (at initialization, and after each crash), and at least every unit decay time TD thereafter. Because the timing of TD is restarted after a crash, it can be done in volatile storage. Instead of cleaning up all the pages after every crash, we could call Cleanup before the first Get or Put to each page, thus reducing the one-time cost of crash recovery; with this scheme the TD interval must be kept in stable storage, however.

For the stable storage actions to work, there must be mapping functions which enumerate the stable pages, and give the representing pages for each stable page. The simplest way to provide these functions is to permanently assign a region of the disk to stable pages, take the address of one representing page as the address of the stable page, and use a simple function on the address of one representing page to obtain the address of the other. For example, if a unit consists of two physical drives, we might pair corresponding pages on the two drives. A more elaborate scheme is to treat a small part of the disk in this way, and use the stable storage thus obtained to record the mapping functions for the rest of stable storage.

To show that the invariant holds, we assume that it holds when stable storage is initialized, and consider all possible combinations of events. The detailed argument is a tedious case analysis, but its essence is simple. Both pages cannot be bad for the following reason. Consider the first page to become bad; it either decayed, or it suffered a bad write during a StablePut. In the former case, the other page cannot decay or suffer a bad write during an interval TD, and during this interval a Cleanup will fix the bad page. In the latter case, the bad write is corrected by the CarefulPut it is part of, unless there is a crash, in which case the Cleanup done during the ensuing crash recovery will fix the bad page before another Put can be done. If both pages are good but different, there must have been a crash between the CarefulPuts of a StablePut, and the ensuing Cleanup will force either the old or the new data into both pages.

Although we make no use of it in this paper, it is interesting to observe that the method used to implement StablePut can actually be used for writing a large amount of data atomically (as long as it fits in half of a unit). Instead of using a pair of pages to represent a stable page, we use a pair of arrays of pages, where none of the pages in one array is decay-related to any page in the other. We need to extend to these arrays the property of disk pages that a write does nothing, succeeds, or leaves the page bad; this is easily done by writing a unique identifier into each page, and checking on a Get that all the unique identifiers are the same. We also need to know during crash recovery which pages are in the arrays; this can be permanently fixed, or recorded in ordinary stable storage.

The stable storage construction can be extended to deal with disk storage that is less well behaved than our model. For instance, suppose that a decay is allowed to change page a from (good, d) to (good, d'), with d' ≠ d. By using four disk pages to represent a stable page, we can handle this possibility. Such increased redundancy can also take care of more frequent decays than we have assumed possible.

To simplify the exposition in the next three sections, we assume that all non-volatile data is held in stable storage. The cost of protecting against all error events is significant, however, and it may not be appropriate to pay this cost for all the data recorded in the system. In particular, client data may not all have the same need for protection against decay: typically, much of it can be reconstructed from other information at some tolerable cost, or has a fairly small value to the client. Hence our system could make provision for recording client data with or without the duplication described above. The same is true for the index which the system maintains to enable rapid random access to the data in files; it is cheaper to provide the necessary redundancy by recording the file address for each page with the page itself, and reconstructing the index from this information in case it is lost. The complications associated with doing this correctly are discussed in section 8.

A stable processor differs from a physical one in three ways. First, it can make use of a portion of the disk storage to store its volatile state; as with other aspects of a processor, long-term reliability of this disk storage is not important, since any failure is converted into a crash of the processor. Thus the disk storage used in this way becomes part of the volatile state.

Second, it makes use of stable storage to obtain more useful behavior after a crash, as follows. A process can save its state; after a crash each process is restored to its most recently saved state. Save is an atomic operation. The state is saved in stable storage, using the simple one-page atomic StablePut action. As a consequence, the size of the state for a process is limited to a few hundred bytes. This restriction can easily be removed by techniques discussed elsewhere in the paper, but in fact our algorithms do not require large process states. There is also a Reset operation that resets the saved state, so that the process will return to its idle state after a crash.

Third, it makes use of stable storage to construct stable monitors [5]. Recall that a monitor is a collection of data, together with a set of procedures for examining and updating the data, with the property that only one process at a time can be executing one of these procedures. This mutual exclusion is provided by a monitor lock that is part of the data. A stable monitor is a monitor whose data, except for the lock, is in stable storage. It has an image in global volatile storage that contains the monitor lock and perhaps copies of some of the monitor data. The monitor’s procedures acquire this lock, read any data they need from stable storage, and return the proper results to the caller. A procedure that updates the data must do so with exactly one StablePut.

Saving the process state is not permitted within the monitor; if it were, a process could find itself running in the monitor after a crash with the lock not set. Since the lock is not represented in stable storage, it is automatically released whenever there is a crash. This is harmless because a process cannot resume execution within the monitor after a crash (since no saves are permitted there), and the single Put in an update procedure has either happened (in which case the situation is identical to a crash just after leaving the monitor) or has not happened (in which case it is identical to a crash just before entering the monitor). As a corollary, we note that the procedures of a stable monitor are atomic.

A monitor which keeps the lock in stable storage is possible, but requires that a Save of the process state be done simultaneously with setting the lock, and an Erase or another Save simultaneously with releasing it. Otherwise a crash will leave the lock set with no process in the monitor, or vice versa. Such monitors are expensive (because of the two StablePuts) and complex to understand (because of the two Saves), and therefore to be avoided if possible. We have found it possible to do without them.

The state of a stable processor, unlike that of a physical processor, is not entirely volatile, that is, it does not all disappear after a crash. In fact, we go further and adopt a programming style that allows us to claim that none of its shared state is volatile. More precisely, any shared datum must be protected by some monitor. To any code outside the monitor, the possible changes in state of the datum are simply those that can result from invoking an update action of the monitor (which might, of course, crash). We insist that all the visible states must be stable; that is, the monitor actions map one stable state into another. Inside the monitor anything goes, and in particular volatile storage may be used to cache the datum. Whenever the monitor lock is released, however, the current state of the datum must be represented in stable storage. As a consequence, the only effect of a crash is to return all the processes to their most recently saved states; any state shared between processes is not affected by a crash. This fact greatly simplifies reasoning about crashes. Note that the remote call mechanism of the next section does not run on a stable processor, and hence does not have this property, even though all the procedures of later sections which are called remotely do have it.

It is easy to construct procedure calls from reliable messages and a supply of processes [7], by converting each call into a call message containing the name of the procedure and its parameters, and each return into a return message containing the identity of the caller and the result. When the messages are unreliable, a little more care is needed: a call message must be resent periodically until a return is received, and duplicate call and return messages must be suppressed. The program at the end of this section has the details. It is written in Pascal, extended with monitors and sets of records, and it calls procedures for communications, a real-time clock, unique identifiers, and passing work to idle processes. For simplicity we assume that all remotely called procedures both accept and return a single value of type Value.

In order to match up calls and returns properly, it is essential to have a source of unique identifiers, so that each call message and its corresponding return can be unambiguously recognized. For this purpose stable storage is required, since the identifiers must be unique across crashes of individual processors. A generator of unique identifiers is easily constructed from a stable monitor whose data is a suitably large counter. By incrementing the stable value in large units (say 1000), using it as a base, and keeping intermediate values in a volatile monitor, it is easy to make the disk traffic negligible. Many machines have a specialized form of stable storage called a real-time clock, which may also be a suitable source of unique identifiers (if it is sufficiently trustworthy). We want the unique identifiers generated by a particular processor to be increasing numbers, and prefer that successive ones differ by 1 almost all the time (see below). Note that an identifier unique to a particular processor can be made globally unique by concatenating it with the processor’s name.

A message can be duplicated by the communication system, and a call (with a different identifier) can be duplicated as the result of a timeout or of recovery from a crash of the caller’s processor. Duplicate return messages are suppressed by keeping a list of pending calls, required anyway for recognizing valid returns. Duplicate call messages are suppressed by observing that processor p’s unique identifiers, which are monotonically increasing, serve as sequence numbers for the call messages, with occasional gaps in the sequence. The receiver keeps track of the largest identifier it has seen from each processor, and ignores call messages with smaller or equal ones. The same mechanism also ensures that when a call is duplicated (by a timeout or crash), the earlier call is executed before the later one, or not at all. This works because the call message for the later call has a larger identifier.

When a receiver crashes, it of course forgets all this, hence when it hears from a processor for which it has no record, it must explicitly request that processor’s current sequence number and discard all earlier messages. We do not know of any reliable methods that avoid such a connection protocol and also make no assumptions about maximum delays in the network.

If messages arrive out of order, this algorithm will cause messages which are not duplicates to be discarded, and performance will suffer. This problem can be alleviated at the cost of k bits per pair of communicating processors, however, by keeping a bit for each of the last k messages which tells whether it has been received. In any reasonable system a very modest value of k will suffice. To preserve the ordering of duplicated calls, the generator of unique identifiers must be advanced by at least k during crash recovery and after a timeout. Otherwise a call message m1 which is generated before the crash or timeout and delayed for a long time, might arrive after a later call message m2 has been processed. If m1.id > m2.id – k, m1 will not be rejected, since it has not been seen before.

The data structures used to implement remote procedures are all volatile (except for the generator of unique identifiers, discussed earlier). Hence when a processor crashes, it will subsequently ignore any return messages from calls outstanding at the time of the crash. Any activations of remote procedures which it happened to be running at the time of the crash will be forgotten, unless they have done Save operations. In the latter case they will complete and send a return message in the normal way, since all the information needed to do this is in the local state of the process running the remote procedure. To make remote procedures a reliable tool in the presence of crashes, some restrictions are needed on the behavior of a procedure being called remotely. These are discussed in the next section.

We assume from this point on that communication between processors is done only with the remote procedure mechanism; that is, there will be no uses of Send and Receive except in the program below.

{ The following program implements remote procedures. It uses Send and Receive for messages, and UniqueId for unique identifiers. The last is also called remotely. }

type Message = record

type ID = 0..2⁶⁴; const timeout = …;

{ The one process which receives and distributes messages }

var m: Message; var s: Status;

while true do begin (s, m) := Receive(); if s = good then

{ Make calls }

monitor RemoteCall = begin

type CallOut = record m: Message; received: Condition end;

var callsOut: set of ↑CallOut = ();

entry function DoCall(d: Processor; a: procedure, args: Value): Value = var c: ↑CallOut; begin

entry procedure DoReturn(m: Message) =

end RemoteCall

{ Serialize calls from each process, and assign work to worker processes. }

type CallIn = record m: Message; work: Condition end;

monitor CallServer = begin

var callsIn, pool: set of ↑CallIn := ( );

entry procedure StartCall(m: Message) = var w, c: ↑CallIn; begin

entry procedure EndCall(w: ↑CallIn) = begin

end CallServer

{ The worker processes which execute remotely called procedures. }

var c: ↑CallIn; New(c); c↑.m. source := nil: EndCall(c); with c↑.m do

{ Suppress duplicate messages. Need not be a monitor, since it is called only from the receive loop. }

type Connection = record from: Processor; lastID: ID end;

var connections: set of Connection := ( );

function OKtoAccept(m: Message): Boolean = var c: ↑Connection; with m do begin

In section 4.4 we defined a serializability property. A standard method for achieving this property is through the use of monitors. However, the stable monitors described in section 5.2 are not strong enough to provide this property. In this subsection we show how stable monitors fail to provide the strong atomic property, why we chose to reject the obvious improvements, and suggest a replacement (compatible actions) for serializability.

This example is wrong. It fails because the actions involve more than one StablePut, which is not permitted for the stable monitors defined in section 5.2. Stable monitors fail in the presence of crashes. Consider what happens when a stable monitor has a number of actions, and through concurrency several of these actions are pending. One of these pending actions will gain access to the data and begin some (compound) statement S. S may be interrupted by a crash, and after crash recovery a different one of the pending actions may gain access. Since S was interrupted by a crash, the monitor invariant is unlikely to be true and thus the new action may misbehave.

This example does not fail because the monitor invariant is false, but for some other reason. Here is a specific example. Suppose we have some data that represents a set, with two actions: Erase, which makes the set empty by removing the elements one at a time, and IsAMember. Suppose that Erase is designed to be interrupted by a crash, and in such a situation it will appear to have removed some but not all members (hence is restartable). Suppose that we start off with a and b in the set, one process M testing a and b for membership in the set, and another process E calling Erase. The following is a possible sequence of events:

In this case, there does indeed appear to have been a series of atomic actions on the data: test b successfully for membership, erase the set, test a unsuccessfully for membership. Unfortunately, M performed the membership tests in the opposite order. Hence these actions are not atomic. Monitor actions in the absence of crashes are guaranteed to be atomic, so it is the crashes that are causing the trouble.

There are two straightforward solutions for this problem. The first is to design the clients of a data structure so that between them they never have more than one pending action on the data (hence no need for monitors at all). This solution is unattractive because it limits concurrency, and because it may be impossible to limit the clients’ behavior in this fashion. A second approach is to store the monitor lock in stable storage: the drawbacks of this are discussed in section 5.2.

Shared data that spans more than one machine presents additional problems. It is possible to protect this data by a monitor, if the lock is kept on some one machine. However, the cost of the additional communication required to acquire and release the lock is likely to be substantial. Also, the data in question is stored on separate machines, and there are algorithms in which some actions on portions of the data can be performed concurrently. Protecting all the data with a single monitor lock would prevent this concurrency.

As a way out of these difficulties, we introduce the concept of compatible actions. Compatible actions provide weaker guarantees than do monitor actions without crashes, but the guarantees are useful, they hold in the presence of crashes, and they can be obtained without storing monitor locks in stable storage.

Consider the actual history of some shared data and the actions on it. Certain actions are started, several may be in progress (or waiting for access if the data is protected by a monitor), and the data goes through a succession of states. This actual history may include crashes, in which some actions are interrupted before returning to their caller. The actions are compatible if there is also a serial history, in which there is no concurrency and each action occurs in isolation. In this serial history, the data goes through a succession of states completely determined by the individual actions, and the result returned by an action will be completely determined by the previous value of the data. The serial history must agree with the actual history in a number of ways:

We do not require that order of the actions in the serial history be consistent with the order in which the actions were called from an individual process (consider the example above).

We shall generally claim compatibility only in the presence of some side conditions that restrict what actions may occur in the same jumble. In addition, we will designate certain actions as strong: any action which completes before a strong action starts will always appear to occur before the strong action, and any action which starts after a strong action ends will always appear to occur after the strong action. An ordinary monitor without crashes provides a set of compatible actions, all of which are strong, and any of which may occur in any jumble. Also, restartable atomic actions on a stable monitor are compatible.

Need an example of the various possible compatible sets for the transaction actions, ranging from singletons to all the actions, with increasing difficulty of implementation and fewer constraints on the user.

Concurrent = not before and not after. Need precise definitions of these.

"Actual history" should be a partial order on events.

Based on stable storage, stable processors, remote procedures, and compatible actions, we can build a more powerful object (stable sets) and a more powerful method for constructing compound actions, from which it is then straightforward to build atomic transactions. The base established in the previous section has the following elements:

In this system the existence of separate processors is logically invisible. However, we want our algorithms to have costs which depend only on the amount and distribution of the data being accessed, and not on the total size of the system. This means that interrogating every processor in the system must be ruled out, for example. Also, the cost of recovering from a crash of one processor must not depend on the number of processors in the system. Rather, it should be fixed, or at most be proportional to the number of processes affected, that is, the processes running on the processor which crashes. Finally, it should be possible to distribute the work of processing a number of transactions evenly over all the processors, without requiring any single processor to be involved in all transactions.

In order to handle arbitrarily large transactions, we need arbitrarily large stable storage objects, instead of the fixed size pages provided by stable storage, and we need arbitrarily large atomic actions instead of the fixed size ones provided by stable monitors. The purpose of this section is to construct these things.

A stable set is a set of records, each one somewhat smaller than a stable page. The stable set itself is named by a unique identifier, and may contain any records. All the operations on stable sets are restartable, and all except Erase return an error indication unless executed between a Create and the next Erase. Stable sets have the following atomic operations:

There are also two non-atomic operations:

We have no need for an operation that removes a single element from a set, and its absence simplifies some of our reasoning.

These operations have all the obvious properties of set operations. Since Enumerate and Erase are not atomic, we specify them more carefully: Enumerate will produce at least all the items Inserted before the enumeration starts, if no Erase has been done; it will not produce any items which have not been Inserted after it is over.

If one of the atomic operations, say A, is done while one of the non-atomic ones, say N, is in progress, A may behave as though it had been done before N started, or after N completed. Each A done while N is in progress makes this choice independently; thus a process doing first A1 and then A2 may find that A1 behaves as though N is complete, and A2 behaves as though N has not started. Even if N fails to complete (because of a crash), A may behave as though N had completed; for example, if Erase has removed an element IsMember will report that it is gone, even though other elements of the set may not yet have been erased.

In spite of these complications, all the actions on a stable set are compatible. The reason for the complications is that tighter synchronization is not needed for our purposes and is tricky to provide. The compatibility is useful to clients because many of the set operations commute. Sensible users of this abstraction will refrain from starting atomic operations while non-atomic ones are in progress.

We have two implementations for stable sets. The first is designed to work efficiently on a single processor, and is extremely simple. We permanently allocate a set of pages in stable storage, with known addresses, to represent stable sets; these pages are called the pool. On each page we store an item of the following type:

The pages of the pool are initialized to empty. The elements of a set ss are those values rr for which there exists a representing page in the pool, that is, one containing an element item i with i.r=rr and (i.s=ss or i.t=ss). To do Insert(ss, tt, rr) we find an empty page and write into it the item (tag=element, s=ss, t=tt, r=rr). To do IsEmpty, IsMember, and Enumerate we search for all the relevant representing pages. To do Replace(ss, tt, oo, nn) we find the page representing (ss, tt, oo) and overwrite it with (ss, tt, nn). Note that Insert and Replace are atomic, as claimed above, since each involves just one Put.

A practical implementation using pools maintains a more efficient representation of the sets in volatile storage, and reconstructs this representation after a crash by reading all the pages in the pool. To make better use of stable storage, it also orders the pages of the pool in a ring, stores several items in each page, implements the Erase operation by writing an erased item rather than removing each item of the set, and recovers the space for the elements of erased sets as it cycles around the ring. The details of all this do not require any new ideas.

The utility of the pool implementation is limited by the need to read all the pages in the pool after a crash. We do not want to read all the pages of all the pools in the system when one processor crashes. Therefore a wide stable set, which spans more than one processor, requires a different approach. We assume that the value of a record determines the processor on which it should be stored (for both sets into which it is inserted), and that the unique identifier of the set determines a processor called the root processor of the set. The idea is to have a stable set called a leaf on each processor, and to use another stable set, called the root and stored on the root processor, to keep track of all the processors involved. All these sets can be implemented in pools. Each record stored in the root contains only a processor name; the records in the leaves contain the elements of the wide set. Operations involving a single record are directed to its processor, and are implemented in the obvious way. IsEmpty, Erase and Enumerate are directed to the root, which uses the corresponding operation of each leaf set in turn. Enumerate calls its procedure argument locally on each leaf machine.

The only trick point is to ensurethat elements are not added to a leaf until its processor is registered in the root set. To accomplish this, the Insert operations check whether the leaf set is empty, and if so they first call the root set’s Insert to add the leaf processor. As a consequence, Insert is no longer an atomic operation within the implementation, but since extra entries in the root set are not visible to the user of the wide set, it is still atomic at that level.

We need to be able to take a complex action, requiring many atomic steps, and make the entire action atomic, that is, ensure that it will be carried out completely once it has been started. If the action R is invoked from a processor which never crashes, and all the actions which can be invoked concurrently with R are compatible, then this goal will be met, because the invoking processor will keep timing out and restarting R until it is finally completed. Thus, for example, if we assume that the client of our data storage system never crashes, then the remote compatible actions of section 5.4 are sufficient to provide atomic transactions. Since we do not want to assume that any processor never crashes, least of all the client’s, something more is needed.

In fact, what is needed is simply a simulation of a processor with a single process that never crashes, and our stable processors already provide such a thing. Consider the following procedure, to be executed by a stable process:

If R is an action compatible with a set of actions S, then A is an atomic action compatible with S. This is clear from a case analysis. If it crashes before the Save, nothing has been done. If it crashes after the Reset, R has been done completely and will not be done again because the saved state has been erased. If it crashes between the Save and the Reset, it will resume after the Save and restart R. The resulting execution sequence is equivalent to a single execution of R, by the definition of a restartable action. If other compatible actions on the same data are going on at the same time, the result is equivalent to a single execution of R together with those other actions, by the definition of compatibility.

The construction of this section completes a sequence begun in section 4.4 with restartable actions, and continued in section 5.4 with compatible actions. We have shown how to construct compound actions with successively stronger properties: first restartable, then restartable in the presence of concurrency, and finally atomic.

In this section we present algorithms for the atomic transactions discussed in section 3. The central idea behind them is that a transaction is made atomic by performing it in two phases:

If a crash occurs after the transaction is committed but before all the changes to stored data have been done, the second phase is restarted. This restart happens as many times as necessary to make get all the changes made. Any algorithm which works in this way is called a two-phase commit [ref Gray].

To preserve the atomic property, the writing of the intentions set must itself be atomic. More precisely, consider the change from a state in which it is still possible to abort the transaction (that is none of the changes have been recorded in the files in such a way that they can be seen by any other transaction), to one in which aborting is no longer possible, and hence crash recovery must complete the transaction. This change is the point at which the transaction is committed. It must be atomic, and hence must be the result of a single Put action. The intentions set may be of arbitrary size, but it must be represented in such a way that its existence has no effect on the file data until this final Put has been done. In addition, care must be taken that the intentions are properly cleaned up after the transaction has been committed or aborted.

This idea is implemented using stable sets and compound atomic actions. The intentions are recorded in a stable set, and the locks needed to make concurrent transactions atomic are recorded in another stable set. The complex operation of committing the transaction (including carrying out the writes) is made into a compound atomic action. To complete the argument, we must show that the various operations are compatible.

We present algorithms for the following procedures to be called by clients: Begin, Read, Write, End, and Abort. The client is expected to call Begin on one of the servers, which we call the coordinator for the transaction. Begin returns a transaction identifier. The client then calls Read and Write any number of times on various servers, directing each call to the server holding the file pages addressed by the call. These calls may be done from separate processes within the client. When all the client’s Write calls have returned, he calls either End or Abort on the coordinator.

If the client fails to wait for all his Writes to return, no harm will be done to the file servers, but their resulting behavior may not be that intended by the client. Each of the actions is designed to be atomic and restartable; thus even in the presence of server crashes, lost messages, and crashed clients they are either fully performed or not performed at all. However, if the client does not repeat each Write call until it returns, he will be unable to determine which Writes actually occurred. Similarly, if he calls End before all Writes have returned, he can not be sure which of the outstanding ones will be included in the transaction.

We use the following data structures:

On each of the server machines we maintain sets containing these objects, and stable monitors protecting these sets, as follows:

We first introduce two entry procedures on the set of transaction flags; these are not accessible to the client:

entry procedure SetPhase( t: TI, desiredPhase: Phase {not nonexistent}) = begin

entry function GetPhase(t: TI): Phase = begin

The SetPhase procedure is an atomic restartable action. It is designed so that the phase of a transaction will go through three steps; nonexistent, running, and then either committed or aborted. Moreover, only setting it to running can remove it from the nonexistent phase, and it will change from running to either aborted or committed exactly once.

Now we introduce the five client callable procedures. Two are entry procedures of the stable monitor for a page. Each should return an error if the page is not stored on this server, but this detail is suppressed in the code.

entry function Read(t: TI, p: PA): Data =

entry procedure Write(t: TI, p: PA, d: Data) =

The other three, which control the start and end of the transaction, are not monitor entry procedures. The End and Abort procedures which complete a transaction do so by calling an internal procedure Complete.

procedure Begin( ): TI =

function End(t: TI): Phase = return Complete(t, committed)

function Abort(t: TI): Phase = return Complete(t, aborted)

function Complete(t: TI, desiredResult: Phase {committed or aborted only}): Phase = begin

A transaction will terminate either through an End or an Abort. Both of these commands may be running simultaneously, either because of a confused client, or because Abort is being locally generated by a server at the same time as a client calls End. Moreover, the remote procedure call mechanism can result in several instances of either End or Abort in simultaneous execution. In any case, the phase will change to either aborted or committed and remain with that value; which of these occurs determines the outcome of the transaction. Thus it is phase which makes Abort and End compatible.

We make four claims:

1. If phase changes from running to committed, then all Write commands completed before End was first entered will be reflected in the file data.
2. The only changes to file data will be as a result of Write commands directed to this transaction.
3. If phase changes from running to aborted, then no Write commands will be reflected.
4. After the first End or Abort completes, the wide stable set for t will have been erased and will remain erased and empty.

Claim 4 follows from the fact that both End and Abort eventually call Erase(t). Thus the set will have been erased. The set can not be recreated because the only call on set creation is in the Begin action, and each time Begin is called it will use a new unique id. Claim 3 follows from the fact that the only writes to file data pages occur in the End procedure; these writes will not occur if the End procedure discovers that phase has been set to aborted. Finally, once phase has been set to aborted, it will remain set to aborted. Claim 2 follows from the fact that only Write can add intentions with a=write to t.

Claim 1 follows from several facts. The fundamental one is that the body of End (following the Save and up to the Reset) is a restartable action. This action has two possible outcomes, depending on the value of phase after the SetPhase. If phase ¹ committed, then the restartable action does nothing. If phase = committed, then it remains so forever, and End will embark on some useful work. This work will include StablePut(i.p, i.d) for any write intention i enumerated from set t. Any Write(t, p, d) command completed before End was called will have made such an entry in t, and the enumeration will produce it. All such entries will be produced because there will be no call on Erase(t) until at least one enumeration has completed without interruption from crashes.

Many refinements to the algorithms of the last three sections can be made. A few have been pointed out already, and a number of others are collected in this section. Most of them are incorporated in a running system that embodies the ideas of this paper [ref Israel et al].

A file can conveniently be represented by a page containing an index array of pointers to data pages, which in turn contain the bytes (or the obvious tree that generalizes this structure). With this representation, we can record and carry out intentions without having to write all the data into the intentions set, read it out, and finally write it into the file. Instead, when doing a Write(p, d) we allocate a new stable page, write d into it, and record the address of the new page in the intention. Then only these addresses need to be copied into the index when carrying out the intentions. This scheme allows us to handle the data only once, just as in a system without atomic transactions. It does have one drawback: if pages are updated randomly in a large file, any physical contiguity of the file pages will soon be lost. As a result, sequential access will be slower, and the space required to store the index will increase, since it will not be possible to compress its contents.

It is easy to see that the sequential for loop in End can be done in parallel, since all the data on which it operates is disjoint.

A more interesting observation is that the writing of intentions into the t and p sets can be postponed until just before End is called. In this way it is likely that all the intentions can be written in a single StablePut, even for a fairly large transaction; that is, the effect of this optimization is that the client’s Write calls will not return until just before the End. A new procedure, say GetReady, would have to be added so that the client can inform the servers that he wants responses to his Writes. We can carry this idea one step further, and move the GetReady call from the client to the coordinator, which does it as part of End before committing the transaction. For this to work, the client must tell the coordinator what responses to Writes he is expecting (for example, by giving the unique identifiers of the calls) so that the coordinator can assume responsibility for checking that the responses are in fact received. In addition, the other servers must return their Write responses to the coordinator in response to his GetReady, rather than to the client.

A consequence of this scheme is that a crash of any server s is likely to force transactions in progress involving s to be aborted, since the intentions held in volatile storage at s will be lost, and the client is no longer repeating his Write calls until he gets the return which indicates that the intentions have been recorded in stable storage. If crashes are not too frequent this is not objectionable, since deadlocks will cause occasional transaction aborts in any case.

A more attractive consequence is that write locks will not be set until just before the End, thus reducing the interval during which data cannot be read by other transactions [ref Gifford]. In order to avoid undue increases in the number of transactions aborted for deadlock, it may be necessary to resort to an "intending to write" lock which delays other transactions also intending to write, without affecting readers. These intricacies are beyond the scope of this paper.

In a practical system it is necessary to time out and automatically abort transactions which run too long (usually because the client has crashed) or which deadlock. The latter case can be detected by some explicit mechanism that examines the locks, or it can be inferred from a timeout. In any case, these automatic aborts add no logical complexity to the scheme described in section 7, which is already prepared to receive an Abort from the client at any time.

When a deadlock occurs because of a conflict between read and write locks, a less drastic action than aborting the transaction holding the read lock is possible, namely to simply notify the client that it was necessary to break his read locks. He then can choose to abort the transaction, reread the data, or decide that he doesn’t really care. It is necessary to require that the client explicitly approve each broken read lock before committing the transaction. The implications of this scheme are discussed in more detail elsewhere [ref Israel, Gifford].

Since the index which maps file addresses into disk addresses is frequently written, it would be nice to avoid the two writes required by straightforwardly implementing it in stable storage. If each data page records its file address, then the index can be reconstructed from the data pages (by scanning the disk), and it will not be necessary to store it redundantly. Some care must be taken, however, with the interaction between this idea and the idea of recording intentions as changes to the index.

The difficulty is that with this latter scheme, a Write for an uncommitted transaction has already constructed a final version of the new data page, indistinguishable from the old version from the point of view of a disk scan which is trying to rebuild a lost index. We cannot solve this problem by modifying the new data page after committing the transaction, since such a modification requires precisely the disk write we are trying to avoid. Instead, we must use the intentions to sort things out when the scan finds two contenders p1 and p2 for the role of page p. If we make the rule that the old page is erased before the intention for the new page is erased, and we can tell that p2 was written after p1, then we can distinguish the following cases:

The necessary ordering of the pages can be obtained by writing a sequence number sn into the header, or in a variety of other ways. Two bits of sequence number are sufficient if interpreted as an integer mod 4, which is incremented by 1 for each new page: p2 follows p1 iff p2.sn – p1.sn = 1 mod 4, and vice versa; exactly one of these conditions must hold. This form of sequence number has the drawback that it is necessary to know p1.sn before writing p2. Using UniqueID instead requires more bits in the header but does not have this drawback.

It is straightforward to made Read and Write work on arbitrary sequences of bytes rather than on pages, and to do their locking to the nearest byte. Some care must be taken with the data structures for the locks, however, since it is not practical to make a lock record for each byte, and hence locks must now be recorded on ranges of bytes.

It is also easy to modify Read so than a transaction can read back the data it has written, rather than seeing the old data as in the program of section 7. Of course, other transactions will still have to wait, or see the old data as discussed in section 8.2.

We have defined a facility (transactions) which clients can use to perform complex updates to distributed data in a manner that maintains consistency in the presence of system crashes and concurrency. Our algorithm for implementing transactions requires only a small amount of communication among servers. This communication is proportional to the number of servers involved in a transaction, rather than the size of the update. We have described the algorithm through a series of abstractions, together with informal correctness arguments.

Eswaren, K. P. et al. The notions of consistency and predicate locks in a database system. Comm. ACM 19, 11, 624-633, (Nov 1976).

Gifford, D.K. Violet: An experimental decentralized system. Submitted to 7th Symposium on Operating System Principles, 1979.

Gray, J.N. Notes on data base operating systems. In Operating Systems, An Advanced Course, American Elsevier, 1978.

Hoare, C.A.R. An axiomatic basis for computer programming. Comm. ACM 12, 10, 576-580, (Oct 1969).

Hoare, C.A.R. Monitors: an operating system structuring concept. Comm. ACM 17, 10, 549-557, (Oct 1974).

Israel, J.E., Mitchell, J.G. and Sturgis, H.E. Separating data from function in a distributed file system. Proc. Second International Symposium on Operating Systems, IRIA, Rocquencourt, France, Oct 1978.

Lauer, H.E. and Needham. R.M. On the duality of operating system structures. Proc. Second International Symposium on Operating Systems, IRIA, Rocquencourt, France, Oct 1978, reprinted in Operating Systems Review 13, 1, 3-19, (Apr. 1979).

Owicki, S. and Gries, D. Verifying properties of parallel programs: An axiomatic approach. Comm. ACM 19, 5 (May 1976), 279-285.