Report
On The Programming Language Euclid
by B. W. Lampsonl, J. J. Hornin and
g2, R. L. London3, J. G. Mitchell1, G. J. Popek4
This report describes the Euclid
language, intended for the expression of system programs which are to be verified.
Authors'
addresses and support:
1.
Xerox Research Center, 3333 Coyote Hill Road, Palo Alto,
CA 94304
2. Computer Systems Research Group, University
of Toronto, Toronto, Canada M5S 1A4 Supported in part by a Research Leave Grant from the
University of Toronto.
3. USC Information Sciences Institute,
4676 Admiralty Way, Marina del Rey, CA 90291 Supported by the Advanced Research
Projects Agency under contract DAHC-15-72-C-0308.
4. 3532 Boelter Hall, Computer Science
Department, University of California, Los Angeles, CA 90024 Supported in part by the Advanced
Research Projects Agency under contract DAHC-73-C-0368.
The
views expressed are those of the authors.
Table of contents
Preface 1
Acknowledgements 1
1.
Introduction 2
2.
Summary of the language 4
3.
Notation, terminology and vocabulary 9
3.1
Vocabulary 9
3.2
Legality assertions 10
3.3
Lexical structure 11
4.
Identifiers, numbers and strings 12
5.
Manifest constants 13
6.
Data type declarations 14
6.1
Simple types 15
6.1.1 Enumerated types 15
6.1.2 Standard simple types 16
6.1.3 Subrange types 18
6.2 Structured types 18
6.2.1 Array types 18
6.2.2 Record types 19
6.2.3 Module types 21
6.2.4 Machine-dependent
records 24
6.2.5 Set types 25
6.2.6 Pointer and collection types 26
6.3 Parameterized types 29
6.4
Type compatibility 31
6.5
Explicit type conversion 32
7. Declarations and denotations of constants and variables 34
7.1
Entire variables 36
7.2
Component variables 36
7.2.1 Indexed variables 36
7.2.2 Field designators 37
7.2.3 Referenced variables 37
7.3
Scope rules 38
7.4
Binding 40
8. Expressions 39
8.1 Operators 43
8.1.1 Multiplying operators 44
8.1.2 Adding operators 44
8.1.3 Relational operators 44
8.1.4 Other
operators 45
8.2
Function designators 45
9. Statements 46
9.1 Simple statements 46
9.1.1 Assignment statements 46
9.1.2 Procedure statements 46
9.1.3 Escape statements 47
9.1.4 Assert statements 48
9.2
Structured statements 48
9.2.1 Compound statements and blocks 48
9.2.2 Conditional statements 49
9.2.2.1 If statements 49
9.2.2.2 Case statements 50
9.2.3 Repetitive
statements 51
9.2.3.1 Loop statements 52
9.2.3.2 For statements 52
9.2.4 Other uses
of binding 53
10. Procedure declarations 55
11. Function declarations 58
12. Programs 60
13.
A standard for implementation and program interchange 63
13.1 Representation of basic
symbols 64
13.2 Standard format for programs 64
13.3. Annotation 65
14.
Implementation notes 66
14.1 Identifiers 66
14.2 Parsing 66
14.3 One-pass translation 66
14.4 Routine parameters 66
14.5 Routines in modules 67
14.6 Constant components of records and modules 67
14.7 Finalization 67
14.8 Inline code 67
14.9 Reference counts 68
14.10 Representation of pointers 68
14.11 Parameterized types 68
References 70
Appendix
A. Collected syntax 71
Appendix
B. Zone Example 78
Preface
This report describes
a new programming language called Euclid, intended for the expression of system programs which are to be verified. Euclid draws heavily on Pascal
for its structure and
many of its features. In order to reflect this relationship as clearly as
possible, the Euclid report has been
written as a heavily edited version of the revised Pascal report.
Proof rules for Euclid
appear in a separate report [London et al 1977]. A Euclid implementation is under
development by the System Development Corporation, 2500 Colorado Avenue, Santa
Monica, California; information may be obtained from Mr. Hugh C. Lauer.
No implementation of
the language has yet been completed, and no Euclid programs of any size have been written. As a
result of experience in implementing and using it, changes in
the language or its defining report
may be made.
This is the third version of the Euclid report; earlier versions appeared in May 1976 and August 1976.
Acknowledgements
Obviously, we are
greatly indebted to Wirth, both for the aspects pf the language which are copied from Pascal, and for the structure
and much of the wording of the report. We are also much in debt to Hoare's work in the areas of
programming language design, axiomatic methods, and program
verification. In particular, we have tried to follow his suggestion that "the language designer
should b_e,,,familiar with many alternative features designed by
others, and should
have excellent judgement in choosing the best... One thing he should not do is to include untried ideas of his
own. His task is consolidation, not innovation." [Hoare 1973].
We have consciously
borrowed ideas and features from Alphard [Wulf, London, and Shaw 1976], BCPL [Richards 1969], CLU
[Liskov 1976], Gypsy [Ambler et al. 1976], LIS [Ichbiah et al. 1974], Mesa
[Geschke and Mitchell 1975], Modula [Wirth 1976], and the SUE System Language [Clark and Horning 1973, Clark and
Ham 1974]; other languages and suggestions
for language features have also undoubtedly influenced our thinking. We have benefitted greatly from comments and criticisms by
numerous individual colleagues on previous
versions of the language and report, and from the comments of the implementors, especially
Lauer.
We are grateful to Prof. Wirth,
and to Springer-Verlag, for permission to use portions of the Pascal report [Wirth 1971,
Jensen and Wirth 1975] in this report.
Our work has been
significantly aided by the Arpanet, which allowed us to maintain effective and rapid communication
in stating and resolving problems, in spite of the wide geographical distribution of the
authors.
1.
Introduction
"There is no royal road to geometry."
Proclus, Comment on
Euclid, Prol. G. 20.
The programming language Euclid has been designed
to facilitate the construction of verifiable
system programs. By a verifiable program we mean one written in such a way that existing formal techniques for proving certain
properties of programs can be readily applied;
the proofs might be either manual or automatic, and we believe that similar considerations apply in both cases. By system we mean
that the programs of interest are part
of the basic software of the machine on which they run; such a program might be
an operating system kernel, the core of a data base
management system, or a compiler.
An important consequence of this goal is that
Euclid is not intended to be a general-purpose programming
language. Furthermore, its design does not specifically address the problems of constructing very large programs; we believe most of
the programs written in Euclid will be
modest in size. While there is some experience suggesting that verifiability
supports other desired goals, we assume the user is
willing, if necessary, to obtain verifiability by giving up some run-time efficiency, and by tolerating some
inconvenience in the writing of his
programs.
We see Euclid as a (perhaps somewhat eccentric)
advance along one of the main lines of current programming language
development: transferring more and more of the work of producing a correct
program, and verifying its correctness, from the programmer and the verifier (human or mechanical) to the language and its
compiler.
The main changes relative to Pascal take the
form of restrictions, which allow stronger statements about the properties of
the program to be made from the rather superficial, but quite reliable, analysis which the compiler can perform.
In some cases new constructions have been introduced, whose meaning can be
explained by expanding them in terms of existing
Pascal constructions. The reason for this is that the expansion would be
forbidden by the newly introduced restrictions, whereas the
new construction is itself sufficiently restrictive
in a different way.
The
main differences between Euclid and Pascal are summarized in the following
list:
Visibility: Euclid provides explicit control over
the visibility of identifiers, by requiring
.the program to list all the identifiers imported into a routine or module, or .exported from a module.
Variables: The language
guarantees that two identifiers in the same scope can never refer to the same
or overlapping variables. There is a uniform mechanism for binding an identifier to a variable in a procedure
call, on block entry (replacing the Pascal with
statement), or in a variant record discrimination. The variables referenced or modified by a routine (i.e.,
procedure or function) must be accessible in
every scope from which the routine is called.
Pointers: This
idea is extended to pointers, by allowing dynamic variables to be assigned to collections, and guaranteeing that two
pointers into different collections can never refer
to the same variable.
Storage allocation: The program can control the
allocation of storage for dynamic variables
explicitly, in a way which confines the opportunity for making a type error very narrowly. It is also possible to
declare that some
dynamic variables should be reference-counted, and
automatically deallocated when no pointers
to them remain.
Types: Types have been generalized to allow
formal parameters, so that arrays can
have bounds which are fixed only when they are created, and variant records can be handled in a type-safe manner. Records are
generalized to include constant components.
Modules: A new kind of record, called a module,
can contain routine and type components, and
thus provides a facility for modularization. The module can include initialization and finalization statements which
are executed whenever a module variable is created or destroyed.
Constants: Euclid defines a constant to be a literal, or an
identifier whose value is fixed throughout the
scope in which it is declared.
For statement: A generator can be declared as a module
type, and used in a for statement to enumerate a sequence of values.
Loopholes: features of the underlying machine
can be accessed, and the type-checking can be
overridden, in a controlled way. Except for the explicit loopholes, Euclid is designed to be type-safe.
Assertions:
the syntax allows assertions to be supplied at convenient points.
Deletions: A number of Pascal features have been
Omitted from Euclid: input-output, seals,
multi-dimensional arrays, labels and gotos, and functions and procedures as parameters.
The only new features in the list which can make
it hard to convert a Euclid program into a legal
Pascal program by straightforward rewriting are parameterized types, storage
allocation, finalization, and some of
the loopholes.
There
are a number of other considerations which influenced the design of Euclid:
It is based on current knowledge of programming
languages and compilers; concepts which are not
fairly well understood, and features whose implementation
is unclear, have been omitted.
Although program portability is not a major goal of
the language design, it is necessary to have
compilers which generate code for a number of different machines, including mini-computers.
The object code must be reasonably efficient,
and the language must not require a
highly optimizing compiler to achieve an acceptable level of efficiency in the object
program.
Since the total size of a program is modest, separate
compilation is not required (although it is
certainly not ruled out).
The required run time support must be minimal, since it
presents a serious problem for verification.
2. Summary
of the language
"Be
sure of it; give me the ocular proof."
Othello III,
iii, 361.
This section contains a summary of Euclid. The
information here is intended to be consistent
with the remainder of the report, but in case of conflict the body of the
report (sections 3-12) governs. Because it is a
summary, many details are omitted, and some general
statements are made without the qualifications which may be found in the body of
the report.
An algorithm or computer program consists of two
essential parts, a description of actions which
are to be performed, and a description of the data which
are manipulated by these actions. Actions are described by statements, and data are described by type definitions. A data type essentially
defines a set of values and the actions which may be performed on elements of that set.
The data are represented by values. A value may be constant, or it
may be the value of a variable. A value occurring in a
statement may be represented by a literal constant, an identifier which has been declared to be constant, an identifier which has been declared as a variable, or an expression containing values. Every
identifier occurring in the program must be
introduced by a declaration.
A constant or variable declaration associates
with an identifier a data type, and either a value or a
variable.
In general, a definition specifies
a fixed value, type, or routine, and a declaration introduces
an identifier and associates some properties with
it. A data type may either be directly described
in the constant or variable declaration, or it may be referenced by a type identifier, in which case this identifier must be
introduced by an explicit type declaration.
A constant declaration associates
an identifier with a value; the association cannot be changed within the scope of the declaration. If the value
can be determined at compile-time, the constant
is said to be manifest;
the expression defining a manifest
constant must contain only literal
constants, other manifest constants, and built-in
operations.
An enumercited type
definition indicates an ordered set of values, i.e., introduces identifiers standing for each value in the set. The simple data types are the enumerated types, the subrange types, and the four standard simple types: Boolean,
integer, char and StorageUnit. The real type has been omitted. For
the first three, there is a way of writing literal
constants of that type: True and False for Boolean, numbers for integers, and
quotations for characters. Numbers
and quotations are syntactically distinct from
identifiers. The set of values of type char is
the character set available in a particular implementation.
The type StorageUnit has values which occupy the minimum unit in which storage allocation is done; this may of course differ from
one implementation to another. Since no operations are defined on StorageUnit
values, nothing more need he said about them.
A type may also be defined as a subrange of a simple type by indicating the smallest and the largest value of the subrange.
Structured
types are defined by
describing the types of their components, and indicating a structuring method. The various structuring methods differ in the
selection mechanism serving
to select the components of a variable of the structured type. In Euclid, there
are five basic structuring
methods available: array, record, module, set, and collection.
In an array structure, all components are of the same type. A component
is selected by an array selector, or computable index. The index type, which must be simple, is
indicated in the array type
declaration. It is usually a programmer-defined enumerated type, or a subrange of the type integer. Given a value of
the index type, an array selector yields a variable or constant of the component type. Every array structure can
therefore be regarded as a
mapping of the index type into the component type.
In a record
structure, the components (called fields) are not
necessarily of the same type. In order that the
type of a selected component be evident from the program text (without executing the program), a record selector is not a
computable value, but instead is an identifier uniquely denoting the component
to be selected. These field identifiers are declared
in the record type definition. Records may include constant as well as variable
components; manifest constant components, of
course, do not need to be stored in each record
instance.
A
record type may be specified as consisting of several variants. This implies that different record values, although declared to be of the
same type, may assume structures which differ in a certain manner. The difference may consist of a
different number and different types of components. The variant which is assumed by a record value is
indicated by a constant of some
simple type which is called the tag.
A module
structure is much like a record, but
may include routines and types as components.
In this way, the operations which are defined on a data structure can be conveniently packaged with the structure.
Module components cannot be accessed outside the module body unless they are
explicitly exported. Thus in a properly written program it is evident from the lexical structure how the state of a
module can be altered.
A set structure defines the set of values which is the powerset of its
base type, i.e., the set of all subsets of
values of the base type. The base type must be a simple type.
Variables declared in explicit declarations are
called static. The
declaration associates an identifier with the
variable, and the identifier is used to refer to the variable. The language guarantees that two identifiers which can legally be used
in the same scope cannot refer to the
same variable, or to overlapping variables. Thus, an assignment to an
identifier cannot change the value of any
other identifier accessible in the same scope.
In contrast, variables may be generated by an
executable statement. Such a dynamic
generation yields a pointer value
(a substitute for an explicit identifier) which subsequently serves to refer to the variable. This pointer may be
assigned to other variables, namely variables
of type pointer. Each pointer variable may assume values pointing to variables
in a single collection
C, all of whose members are of the same type. It
may, however, also assume the value C.nil, which points to no variable. Because
pointer variables may also occur as components'
of structured variables, which are themselves dynamically generated, the use of pointers permits the representation of finite
graphs in full generality. Although the
language cannot guarantee in general that two pointer variables do not refer to
the same variable, it can make this guarantee for two
pointers in different collections.
A zone can be associated with each collection to provide
procedures for allocating and deallocating the storage required by variables in
that collection; if the zone is omitted, a standard
system zone is used. The program may free a dynamic variable explicitly, in
which case the program is responsible for ensuring that there will be no
further references to the non-existent
variable. .Alternatively, the collection may be reference-counted, in
which case each variable is
automatically freed when no pointers to it remain. The main advantage of reference-counted variables, as compared with explicit
deallocation, is that the correctness of the
deallocation does not have to be verified.
Throughout this report, the word variable means
a container which can hold a value of a specific
type. A variable may or may not be associated with an identifier. A constant, by contrast, is simply a value of a specific type. The
fundamental difference is that assignment to a
variable is possible.
A type declaration may have formal parameters;
such a parameterized declaration
represents a set of types, one of which
is specified each time the type is referenced and actual parameters are supplied for the formals.
Two types are the same if their definitions are
identical after any type identifiers which are not
opaque have
been replaced by their definitions, and any actual parameters and any identifiers declared outside the type have been replaced
by their values. A type identifier is opaque
if it is a module type, or is exported from a module.
The most fundamental
statement is the assignment
statement. It specifies that a newly
computed value be assigned to a variable (or a
component of a variable). The value is
obtained by evaluating an expression. Expressions consist of variables, constants, sets,
operators and functions operating on the denoted
quantities and producing new values.
Variables, constants, and functions are either
declared in the program or are standard entities.
Euclid defines a fixed set of operators, each of which can be regarded as
describing a mapping from the operand
types into the result type. The set of operators is subdivided into groups of:
1. arithmetic operators of
addition, subtraction, sign inversion, multiplication, division, and computing the remainder (mod).
2. Boolean operators of
negation (not), conjunction (and), disjunction (or) and implication
(->).
3. set operators of
union, intersection, set difference, and symmetric, difference (xor).
4. relational operators of
equality, inequality,
ordering, set membership and set
inclusion. The results of relational operations are of type Boolean.
The procedure statement
causes the execution of the designated procedure
(see below).
There
are two kinds of escape statements: an exit statement is used
to terminate a loop, and a return
statement to terminate a
routine. An escape statement may be qualified by a when clause, which
causes termination only if a Boolean expression is True.
Assignment,
procedure, and escape statements are the components or building blocks of structured statements, which specify sequential, selective, or repeated
execution of their components.
Sequential execution of statements is specified by the compound statement;
conditional or selective execution by the if statement and
the case statement; and repeated execution
by the loop statement and the for
statement. The if statement serves to
make the execution of a statement dependent on the value
of a Boolean expression, and the case statement
allows for the selection among many statements according to the value of a selector. The discriminating case statement provides a
safe way of discriminating the current variant of
a variant record. The for statement is used when a bound on the number of iterations is known beforehand, and the loop statement
is used otherwise.
A block
can be used to associate declarations with
statements. The identifiers thus declared have
significance only within the block. Hence, the block is called the scope of
these identifiers, and they are said to be local to the
block. Since a block may appear as a statement,
scopes may be nested. An if, case, for or loop statement, or a module type declaration, also defines a scope in a similar way.
A block can be named by an identifier, and be
referenced through that identifier. The block
is then called a procedure, and its declaration a procedure declaration. However,
an identifier which is not local to a given
procedure body is accessible in that body only if it is accessible in the immediately enclosing scope, and
it is pervasive in some enclosing scope or
it is
explicitly imported into the given procedure body.
A procedure has a fixed
number of parameters, each of which is denoted within the procedure by an
identifier called the formal
parameter, which is local to the
procedure body. Upon an activation of the procedure
statement, an actual quantity has to be indicated for each parameter which can be referenced from within the
procedure through the formal parameter. This
quantity is called the actual
parameter. There
are two kinds of
parameters: constant parameters and variable
parameters; routine and type parameters are not
allowed. In the first case, the actual parameter is an expression which is
evaluated once. The formal parameter represents a local
constant whose value is the result of this evaluation. In the case of a
variable parameter, the actual parameter is a variable and the formal parameter is bound to this variable. Possible
indices or pointers are evaluated before execution
of the procedure.
Functions are declared analogously to procedures; procedures and
functions are collectively called routines. The
main difference lies in the fact that a function yields a result, which may be of any assignable type and must be specified in the
function declaration. Functions may
therefore be used as constituents of expressions. Variable formal parameters
and imported variables are not permitted within function declarations; as a
consequence, functions cannot have side
effects.
Since Euclid is intended for the writing of
programs which are to be verified (either mechanically
or by hand), there are a number of explicit interactions between the language and the verifier, in addition to the many aspects of the
language which have been motivated by the
desire to ease verification. These explicit interactions fall into two main
categories:
embedding of assertions in
the program: the special symbols assert, invariant, pre and post introduce assertions. These may be written as comments
which are ignored by the compiler. Presumably
they will be used by the verifier, which can take advantage of their relationship to the structure of the
program. Alternatively, an assertion may be written
as a Boolean expression, which is compiled into a run-time check if the checked option has been specified for an
enclosing scope.
compiler-generated assertions: in cases where
the compiler needs to be able to assume
that some condition holds, but is unable to deduce that it does, the compiler
may generate an assertion (in a new listing of the program) for the verifier,
and then proceed as though confident of its truth. The
legality of the program will then depend
on the validity of the compiler-generated assertion. Each case in which such an assertion may be generated is spelled out in this
report.
3. Notation, terminology, and vocabulary
"The best words in the best
order."
Coleridge.
The syntax is described in a modification of
Backus-Naur form, in which syntactic constructs
are denoted by English words or phrases, not enclosed in any special marks. These words also suggest the nature or meaning of the
construct, and are used in the
accompanying description of semantics. Basic
symbols of the language are written in
boldface or enclosed in quote marks; e.g., begin
and ":". Possible repetition of a construct is
indicated
by enclosing the construct within metabrackets { and } . Possible
omission of a
construct is indicated by enclosing the construct
within metabrackets [ and ] The word
empty denotes the null sequence of symbols.
The grammar defining the syntax of Euclid is distributed
throughout this report; for convenient
reference, it has also been collected in Appendix A.
3.1 Vocabulary
The primitive vocabulary of Euclid consists of
basic symbols classified into letters, digits,
and special symbols. Note that this vocabulary is
not the character set. The character set is
implementation dependent, and each implementation
must define, in its character set, distinct
representations for all the basic symbols. Suggestions for doing
this in some common cases may be found in
section 13.
Each implementation must specify a single break character which can be used within an identifier.
Two identifiers are similar if they are composed of the
same sequence of characters, except for
changes from upper to lower case letters or vice versa, and for the presence or absence of break characters. The intended use of
the break character is to visually separate
an identifier into its component parts. In an implementation which can print upper and lower case letters, a transition from
lower to upper case can also be used for this
separation. It is recommended that this convention be used when possible, in preference to the explicit break character, for
implementations which have lower case letters;
obviously it cannot be used if the entire
identifier is upper case, for example. Thus, an
identifier might be represented as
alpha
Beta using
96-character ASCII, with capitalization as the break.
ALPH
A_BETA using the IBM PL/l character set,
with as the break.
ALPHA\BETA using
the Model 33 Teletype character set, with \ as the break.
All of these identifiers would be similar to the
identifier ALPHABETA. With these conventions,
it is possible to convert from one representation to another in a reasonable
way (see 13.).
Each time an identifier is used, it must be
written in exactly the same way (i.e., with the same
capitalization and use of break characters) as it was written when
it was declared.
However, another identifier which is similar according to the
above rules
may not be
declared in any scope in which the first
identifier is accessible (see 7.3).
The following capitalization convention is
generally used in this report: type and routine
identifiers begin with a capital letter (except
for certain standard types); other identifiers
begin with a small letter. This
convention is not part of the definition of Euclid, hOwever.
letter ::= "A" I "B" I
"C" I „D,. "E" I „F,. '°G" "I-I" I "I" I
"1" I "K" I "L,"
"M" I ,.N,. "0"
1 "R" I "Q" I "R" 1 "S" I ".I,,,
"U" I "V" I "W" I ,.X,.
"Y" 1
"Z"
1"a" 1 "b" 1"c" 1 "d" 1"e"
1"f" 1 "g" 1"h" I"i" I
"}" 1 "k" I "I" 1 "m" 1"u" 1 "0" I "p"
I "a" I "r"
I "s" I
IT° 1 "u" I "v" 1 "w" 1
"x" I "Y" I "z"
octalDigit ::= "0" 1 "1" I "2" I "3" 1 "4" 1 ""5.. "6" 1 "7"
digit ::= octalDigit
1 "8" I "9"
hexDigit ::= digit I "A" 1 .,B,. "C" I ,.D,. "E" I "F"
breakChar ::= <some
implementation-dependent character not a letter or digit>
specialSymbol ::=
"+" I
"" 1 "*" I "=" I "<" I ">" I "<="
1 ">=" "->"
1 "(" I ")" I
"{"
I„}„ 1 ":=” I
"" I "" ":"
I ":" 1„ ° " I "c"
I "=>"
I "<<=" I "S" I "#" I
wordSymbol
wordSymbol ::=
abstraction I aligned 1 all 1 and I any
I array I assert I at I begin I bind I bits bound
I case I checked 1 code 1 collection I const I counted I decreasing dependent I discriminating I div I else I elseif I
end I exit 1 exports I finally
for I forward 1 from 1 function I if 1
imports 1 in I include I initially 1 inline invariant 1 loop I machine I mod 1 module 1 net l
of 1 on 1 or 1 otherwise packed 1 parameter I pervasive I post I pre 1
procedure I readonly 1 record
return I returns I set I then 1 to 1 type I unknown 1 var 1 when I with I xor
The construct
"{" <any
sequence of symbols not containing "}"> "}"
may be
inserted between any two identifiers, literal constants (see 4.), or special
symbols. It is called a comment, and
may be removed from the program
text without altering its meaning.
The symbols "{" and "}" do not occur otherwise in the
language.
Any verification system
which accepts Euclid programs as input may define a convention for distinguishing comments which have special meaning for
the verifier. One reasonable convention is that every comment in which a
certain character appears as the first character after
the is
intended for the verifier.
The word routine
is used
as a synonym for the phrase "procedure or function."
3.2 Legality assertions
Throughout this report, various restrictions
will be placed on legal Euclid programs. Many of
these restrictions cannot be checked syntactically, and in some cases they
involve dynamic conditions that are
difficult (or impossible) to check statically. Nevertheless, programs that violate them are not considered to be meaningful Euclid
programs. It is the responsibility of the
compiler to verify as many of these properties as it can, and to produce
Boolean expressions called legality assertions for
those it cannot. Thus, any program whose legality assertions can all be verified is a legal Euclid program,
with well-defined semantics. Note that
legality assertions are produced only for conditions specified in this report.
If checked is specified for a scope and
not overridden by an inner not checked (see 6.2.3 and 9.2.1), all legality assertions in the block, and all
programmer-supplied assertions which are Boolean
expressions, are compiled into run-time checks, as an aid in detecting illegal programs, even before the verification process is
complete.
3.3
Lexical structure
The
text of a program is built up out of declarations and statements, collectively
called units, according to the syntax specified below. In
general units are separated by semicolons. The syntax is constructed in such a way that a unit may always be legally followed by a semicolon. In order to make it unnecessary to
write semicolons between units which appear on separate lines, a semicolon is automatically inserted at the end of a
line whenever the last token
of the line could be the end of a unit, namely one of:
identifier, literal constant, ), t, exit, return, forward, or
end possibly followed by if,
loop, case, record, or module,
and the
first token of the next line could be the beginning of a unit, namely one of:
identifier, literal constant, abstraction,
assert, begin, bind, case, const, exit, finally,
for, function, if, initially, inline, invariant, loop, machine, pervasive, procedure,
return, type, var or with.
Commas are used as separators in enumerated
types, case label lists, element lists, and parameter
lists, and within declarations in identifier lists, bind lists, and
import/export lists.
There are several kinds of brackets which are used to
group declarations and statements for various
purposes. The following list gives the unique closing bracket for each opening bracket.
|
if
loop
case =>
begin
code record
module
|
end
if
end loop end case
end
caseLabel
end, or end
routineldentifier whenever the block is the body of a routine
end routineldentifier.
end record, or end
typeldentifier whenever the record definition is the declaration of a type identifier.
end module, or end
typeldentifier whenever the module definition is the declaration of a type identifier.
|
4. Identifiers,
numbers and strings
"And twenty more such names as these
Which never were nor no man ever
saw."
The Taming of the Shrew, Induction, ii, 95.
Identifiers serve to denote constants,
variables, types, and routines. Their association must be unique within their scope of validity, i.e., within the
scope in which they are declared (see 6, 7.3).
identifier
::= letter { letterOrDigit }
letterOrDigit
::= letter I digit I breakChar
The usual decimal notation is used for numbers,
which are the literal constants of the data type
integer (see 6.1.2.). Numbers may also be written in octal or hexadecimal
notation. Note that unsigned numbers are always positive;
a negative manifest constant can be written as an
expression, e.g., -14.
unsignedNumber
::= digit { digit } I
octalDigit octalDigit } "#8" I
digit { hexDigit } "#16"
Examples:
1 100 717#8 OCAD1#16
123#16
Sequences of characters enclosed by quote marks
are called literal
string constants. They are the literal constants of the standard type string (see
6.2.2). A character code, whether or not it
is in the printing character set, can also be represented in a literal string
constant as follows:
$ddd, where each d stands for a
decimal digit, represents the character code with the decimal representation ddd. Note: char.Ord($$ddd) = ddd (see
6.1.2).
For convenience, $S, $T, $N, $$, $' represent space, tab,
newline, $, and ' respectively. The $ddd construction can
be used only in a machine-dependent module (see 6.2.3).
literalString
::=" ' " extendedCharacter } " ' "
extendedCharacter
::= character I "$" extension
extension ::= digit
digit digit I "S"
I "T" I "N" I "$" I "
Examples:
1.1 'Here comes a null: $000 and there it went'
'Euclid'
• 'THIS IS A STRING"This$Sis$Sa$Sstring'
A single character preceded by a dollar sign is a
literal constant of the standard type char (see
6.1.2). The $
convention may also be used in these constants.
literalChar
::= "$" extendedCharacter
Examples:
$a $$S
{space character} $$000 {the NUL character} $" $$$
Manifest constants
"One here will constant be, Come wind, come weather."
Pilgrim's
Progress
A manifest constant is a literal constant or an
expression which can be used in place of a literal
constant. The value of a manifest constant can be computed in a straightforward
way at compile time. Thus, a manifest constant expression
may not involve any functions, except the
standard ones defined in this report. A general constant, by contrast, has a
value which is fixed during the lifetime of the scope
in which it is defined, but may be computed in an
arbitrary way at the beginning of that lifetime.
literalConstant ::=
unsignedNumber I literalString I literalChar I enumeratedValueld manifestConstant ::= literalConstant I
manifestConstantExpression manifestConstantExpression
::= expression
Examples:
-100 'Euclid' red 3*Co/or.Ord(Colorlast)
6. Data types
"What
is written without effort is in general read without pleasure."
Johnson
A data type determines the set of values which
variables and constants of that type may assume,
and the set of basic operations that may be performed on them. A type
declaration associates an identifier
with the type. The type identifier is considered to denote the same type as its definition, unless it is declared as a module
type (see 6.2.3) or is exported from a module, in which
case the identifier denotes a different type; type equivalence is discussed in detail in 6.4. Parameterized types are introduced in
6.3.
A type declaration introduces a new scope in
which the formal parameters of the type, if any,
are declared (see 6.3). If the type definition is a module type, the definition
is a second, closed scope (see 7.3), and identifiers
declared outside it are inaccessible unless imported.
If the type definition is not a module type, however, its scope is the open
scope of the declaration (or possibly a second, open
scope for a record definition), and importing is
not necessary (or possible).
An identifier must be declared before it is used. When there are mutually recursive routines or types, however, it is impossible to give the definition of every identifier before its
use. In this situation, a definition of forward may be given instead, and later
another declaration, of the form type (or procedure
P=..., or function Fr...) must appear to provide
the true definition. Between its forward and true definitions, or within its
own definition, a type may only be used as the object
type of a collection, or to declare a formal parameter.
If an identifier declared with forward has parameters, these must appear in the
forward definition and must not be repeated in the true "definition.
A type declaration may not contain variable
identifiers which are free, i.e., declared outside the type declaration, except that a module definition may
explicitly import variables. As a consequence,
an unparameterized type identifier denotes the same type throughout the scope
in which it is declared, and the type denoted by a parameterized type
identifier depends only on the values of the actual
parameters. Note, however, that the same type identifier may denote different types in different scopes, e.g., in
different instantiations of a routine or a module.
All types (except integer) automatically acquire
components when they are declared. For example,
an array type T has the component T.lndexType (see 6.2.1). Any component
of a type is automatically also a component of every
constant or variable of that type. Thus if e is a
constant or variable of type T, eindexType is the
same as T.IndexType.
This report specifies the standard representations, in terms of bits, for the values of
certain types. These specifications are given so that
machine-dependent records and machine-code procedures
can be sensibly defined, and so that the effect of an explicit type conversion
can be predicted. The following contexts are defined
as sensitive:
a variable component of a
machine-dependent record (see 6.2.4) a variable declared at a fixed address
(see 7.)
an actual parameter or
result of a machine-code routine (see 10.)
the actual parameter or
result of an explicit type conversion (see 6.5)
A type may not appear in a sensitive context
unless its standard representation is specified, either
in this report, or explicitly by the implementation. Except in these sensitive
contexts, there is no way for a Euclid program to determine
the standard representation of any value, and an
implementation is therefore free to use other representations, provided that it
converts each value to the standard
representation when it appears in a sensitive context.
type ::= simpleType I
structuredType I pointerType I parameterizedTypeReference
typeDeclaration ::= type typeldentifier formalParameterList =
preAssertion typeDefinition
typeldentifier
::= identifier
typeDefinition ::= type I forward
There are two components
implicitly declared for each type other than integer:
T.size the result, of type integer, is the number of
StorageUnits (see
6.1.2) required for the representation of a
variable of type T.
T.alignment the result, of type
integer, is the required alignment of variables
of type T, in StorageUnits.
Thus, if p :
pType is a pointer to such
a variable, then (AddressType<<=pType(p)) mod
pType.alignment=0.
There is a component implicitly declared for each variable or constant: x.itsType the type of x
6.1. Simple types
There are no type variables in Euclid. However,
a type may be a component of a module (see
6.2.3), and hence may be referenced by a field designator (see 7.2.2), as well
as by an identifier.
simpleType ::= enumeratedType I standardSimpleType I subrangeType I derivedSimpleType
derivedSimpleType ::= [ containingVariable
"." I simpleTypeldentifier simpleTypeldentifier
::= identifier
6.1.1.
Enumerated types
An enumerated type defines an ordered set of
values by enumeration of the identifiers which
denote these values. There must be at least two such identifiers. The
identifiers are declared as constants in the current scope. if the current
scope is a type declaration of type T, for which the
enumerated type is the definition, however, the identifiers are declared in the enclosing scope instead, i.e., the scope in which T is declared. In any case, the identifiers may not be used for any other purpose in the scope in
which they are declared.
The standard representation of the ith identifier
(counting from 0) in the enumeration is the
same as the representation of the unsigned integer i. Thus, if T is an enumerated
type,
T.first is represented
exactly like the integer 0.
enumeratedType ::=
"(" enumeratedValueld { "," enumeratedValueld }
")" enumeratedValueld
::= identifier
Examples:
type Color = (red, green, blue, orange, yellow, purple)
type Suit = (club,
diamond, heart, spade)
type Day = (Monday,
Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday) type SexType = (female, male)
type Classification =
(confidential, secret, topSecret)
type Device = (disk, display, keyboard, printer, tape)
Components implicitly declared for each enumerated and subrange (see
6.1.3) type T are:
 the
first value (in the enumeration) the last value (in the enumeration)
the
first value (in the enumeration) the last value (in the enumeration)
the value succeeding x (in the enumeration).
T.Succ(T.last) is undefined if T is an enumerated type, or T is a subrange of an enumerated
type U and T.last=U.last.
the value preceding x (in the enumeration).
T.Pred(T.first) is undefined if T is an enumerated type, or 7' is a subrange of an enumerated type U and
T.first=U.first.
an
unsignedlnt which is the ordinal number of the value x in the enumeration of T. Thus,
T.Ord(T.first)=0.
For instance, Suit.last is spade, and Day.first is Monday.
6.1.2.
Standard simple types
The following types are standard in Euclid, and are
pervasive throughout all programs (see 7.3):
integer Its values are the positive and negative
integers, in the mathematical sense. It is not
possible to declare a variable to be of type integer. instead, variables can be declared to be of some suitable subrange type. Constants
of type integer may be declared, however, and numbers
are literal constants of type integer.
|
signedlnt, unsignedlnt
|
Every
implementation has two standard types, signedlnt and unsignedlnt; they are ordinary subranges of integer which are pre-defined
for convenience. These are implementation-defined; the intention is
that they should be large subranges of integer type which can be handled
efficiently by the machine, and which contain:
for signedlnt. equal numbers of positive and negative
numberS, or perhaps one more
negative number.
for unsignedlnt, 0 and no
negative numbers.
|
|
Boolean
char
|
An operation is called well-behaved if its operands are in the range signedint,
or unsignedInt, and it yields an integer result in the same range. An implementation must support the evaluation of
any expression in which all
the operations are well-behaved (see 8.1). An implementation may also support the evaluation of expressions involving larger
integers (e.g., double-precision
integers), but this is not required. It is recommended, however, that on machines which have unsignedInt.0..216-1,
at least double-precision
integers should be supported.
If T is defined by
type T = m n, for any manifest constants
m, n>=0, and i is a value of
type T, the standard representation of i is the ordinary binary representation of
the integer i, filled
out on the left with any number of extra
zeros. The standard representation of a signed integer must be defined by
the implementation, but is not defined in this report.
There
are two standard functions defined on any subrange of integer: Abs(x) returns an integer which is the
absolute value of x. Odd(x)
returns a Boolean which is True if and only if x is odd.
Its values are the truth values denoted by the
identifiers False and True. It is defined
by type Boolean = (False, True).
It is an enumerated type whose values are a set
Of characters determined by the
implementation. They are denoted by the characters themselves preceded by
a dollar sign (see 4.).
There is a standard function Chr(x:
0..char.Ord(char.last)) with the property that
char.Ord(Chr(x))=x.
Warning: the ordering of the values of type
char is implementation dependent. Use of this
ordering in comparisons of chars, subranges of chars, or the Chr and char.Ord functions, will in general
result in non-portable programs. Unlike most
other machine-dependent features of Euclid, this one is
not restricted to machine-dependent modules.
|
StorageUnit
This is the basic unit for storage allocation (see 6.3). There are no distinguishable values of this type, and no operations
are defined on this type. Thus, a StorageUnit variable
simply serves to occupy a known amount of
space. The standard representation of a StorageUnit is not defined.
There are two standard components of the type StorageUnit:
sizeinBits, an integer constant which defines the number
of bits in a StorageUnit.
Address, a function
declared by
function Address (A:array 0..n of StorageUnit) returns
Add ressType,
which returns the machine address of A(0). It may only be
used in a machine-dependent module.
AddressType This is an unsigned subrange of
integer, large enough to hold a full machine address;
i.e., a value returned by the function StorageUnit.Address.
6.1.3.
Subrange types
A type may be defined as a subrange of another
simple type by indication of the smallest and the
largest value in the subrange. The first constant specifies the lower bound,
and the second the upper bound. If type A is a subrange of type B, and
type B is a subrange of type C, we
say that A is also a subrange of C. The Succ, Pred, first and last
components are defined for all subrange
types. If A is a subrange of B, and a is of type A and b is of type B, and a=b, and the standard representation of b is defined, then the standard representation of a is the same as the standard
representation of b.
subrangeType ::= constantSum ".."
constantSum constantSum ::= sum
Examples:
type OneToOneHundred = 1 .. 100
type SymmetricRange = -10 .. 10
type Primary = red .. blue {the
values of a Primary are red, green, and blue} type ScreenPosition = 1 .. 525 {y coordinate
for display screen}
6.2. Structured types
A structured type is characterized by the type(s)
of its components and by its structuring method.
Moreover, a structured type definition may contain an indication of the
preferred data representation: if a definition is prefixed with the symbol
packed, this is a hint to the compiler that
storage should be economized even at the price of some loss in efficiency of
access, and even if this may expand the code necessary for accessing components
of the structure.
Adding occurrences of packed
may make a legal program into an illegal one
(because of type compatibility (see 6.4) or
if a component of the structure has been renamed as an entire variable (see 7.4)), but will not otherwise change the
meaning of the program.
structuredType
::= [ packed unpackedStructuredType
I derivedStructuredType
unpackedStructuredType arrayType
I recordType I moduleType I
mdRecordType I setType I
collectionType
derivedStructuredType ::= [containingVariable
"."] structuredTypeldentifier structuredTypeldentifier
::= identifier
6.2.1.
Array types
An array type is a structure consisting of a
fixed number of components which are all of the same type, called the component type. The elements of the array are designated by indices,
values belonging to the index type. The array type definition specifies both the component
type and the index type.
The
standard representation of an unpacked array A of type array I of C is defined as follows. Let
t.C.size+(C.alignment-1), and s=t-(t mod
C.alignment). Then
successive
components
of A
occupy successive groups of s StorageUnits, with no unoccupied StorageUnits in between. A(I.first) occupies the
first s StorageUnits, i.e.,
the ones with the smallest
machine addresses, and A(I.last) occupies the last s StorageUnits, i.e., the ones with the largest
machine addresses. Each component is aligned in the same way as a variable of type C. The entire array thus occupies
max(0,e(Llast - /.first + 1)) StorageUnits. The standard representation of a packed array is not defined.
arrayType ::= array
indexType of componentType indexType ::= simpleType
componentType ::= type
There are two standard
components of an array type T:
T.IndexType the
index type
T.ComponentType the
component type
Like
other components of types, they are also components of any variable or constant
of the type (see 6.). Thus if a is a variable of type T, then aindexType is the same as T.IndexType, and likewise for ComponentType.
|
Examples:
type
type type type
|
ArrayO = array 1 .. 100 of signedInt
Arrayl = array -10 .. 10 of 0 .. 99
Array2 array Boolean of Color
NameTable = array OneToOneHundred of string(50)
|
6.2.2.
Record types
A record
type is a structure consisting of a fixed number of components, possibly of different types. The record type definition
specifies for each component, called a field, its type
and an identifier which denotes it. The scope of these field identifiers
is the record definition itself. They are also accessible
within a field designator (cf. 7.2) referring to a record variable or constant of this type. Record
components may be constants or variables. Components other than variables are accessible within a field designator
referring to the type
itself, as well as in a designator referring to a variable.
For the syntax of constant and variable
declarations, see 7. If the record type appears as the definition of a type identifier, it must end with the
clause end identifier;
otherwise it must end with end record.
The size of a record containing an unpacked array
is equal to some constant value, independent
of the array size, plus the size of the array. The standard representation of a
record is not defined.
recordType
::= record fieldList endRecord endRecord end
record I end identifier
variantPart ] [ , ]
fieldList ::= , [ recordDeclaration [";"] ] [
recordDeclaration ::= pervasive recordDeclarationPart
"," per-Vasive recordDeclarationPart
}
recordDeclarationPart constantDeclaration
I variableDeclaration
pervasive
::= pervasive I empty
A record type may have several variants. In this case a constant of some simple type must be used as a selector in a case construction which
enumerates the possible variants. This constant
is called the tag,
and its value indicates which variant is assumed
by the record variable at a given time.
Each variant structure is identified by a case label which is a set of manifest constants of the type of the tag. Usually the
tag will be a formal parameter of the type
declaration in which the case appears (see 6.3). When a variable of the record
type is declared, however, the tag must be a manifest
constant, or any.
The case label lists must be disjoint.
Furthermore, the union of the lists must exhaust the enumerated type of the tag, unless there is an otherwise
variant, in which case all the tag values not
mentioned explicitly are lumped under that variant. The case label following
the end of the variant must be one of the labels specified by the
case label list.
variantPart
::= case tag of variant { ";" variant } [ otherwiseVariant ] [
";" ] end case variant caseLabelList
"=>" fieldList end caseLabel I empty
caseLabelList caseLabel ","
caseLabel }
caseLabel ::=
manifestConstant I subrangeType
tag ::= constant
otherwiseVariant ::= otherwise ".>" fieldList
Examples:
type Date = record
var day 1 .. 31
var month: (Jan, Feb,
Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec) var year 1900 .. 2100
end Date
type stream (dev: Device) = record
case dev of
display =>
var first, last:
DisplayControlBlock {not
defined in this report} var height: ScreenPosition ScreenPosition.first
var nLines: 0 .. (ScreenPosition.last)/8
end display
tape,
disk =>
var file: FileHandle {not defined in this report}
var position..
unsignedInt := 0
var buffer array 0 .. 255 of char
end tape
keyboard =>
var buffer. array 0 .. 20 of char
var bufFirst, bufLast:
buffer.IndexType :=
buffer.IndexType.first end keyboard
otherwise => {null fieldList}
end case
end stream
There are three pervasive
standard types having to do with strings, declared as follows.
type Stringlndex = 1 stringMaxLength
type StringLength = 0 stringMaxLength
type string(maxLength: StringIndex) = record var length: 0 .. maxLength 0;
var text: packed array 1 .. maxLength of char end string
Literal string constants
are of type string, with length equal to the number of
characters. The maxLength of a literal string constant is chosen to make its type
suitable for the context in which it appears; it must not be less than the length, however. Routines can readily be defined to extract substrings, do pattern matching, or
perform any other desired operations on
strings (see 10. and 11. for examples). Furthermore,
these routines might be
machine-coded for
efficiency. The value of
the pervasive manifest constant
stringMaxLength is implementation-defined.
6.2.3
Module types
A module type is a generalization of a record
type. Module components may be declared as constants,
variables, routines, or types. These declarations have the same form and the
same meaning as the declarations in a block. Thus, a module
serves as a package for a collection of
related objects. A module type is always opaque; i.e., it is not the same as
any other type (see 6.4). Thus, two different module definitions always define
different types, even if the definitions are
textually identical.
Identifiers declared in a module are not known
outside unless they are exported explicitly, so the packaging supplied by the module also provides
protection against improper use of components
which are intended to be known only within the module definition. An exported identifier x is
accessible (but only within a suitable field designator) in any scope in which the module type is accessible. A constant
identifier is always exported as a constant;
this may be specified by a binding condition of const, or the binding condition
may be omitted. A variable identifier may be
exported as a variable, using the binding condition
var, or as a readonly variable, using the binding condition
readonly or omitting the binding condition (see 7). A variable may not be
exported as a constant. No two variables in the
union of the import and the export lists of a module may overlap (see 7.4).
A constant or variable identifier may not be
exported unless its type is exported, or is accessible
in the scope S enclosing the module definition; the itsType component of an exported constant or variable is automatically exported.
Similarly, a routine identifier may not be
exported unless the types of its parameters and results are exported or
accessible in S.
When a type T is
exported from a module M, it is always opaque outside
its defining module; i.e., it is not the
same as any other type (see 6.4). Thus all operations on values of type T, other than possibly assignment and equality tests, must be
performed by routines defined in M. The export item for
a type may specify, in an appended with clause, that it is to be exported with assignment, equality or both; an
operation not specified is not exported. If
assignment is not exported, then T is not assignable;
i.e., outside M constants or constant parameters
of type T cannot be declared, and variables of type T cannot appear on the left side
of an assignment statement. Furthermore, Ts field identifiers (including
standard ones, like size) are not accessible outside 41,
unless the with clause specifies that they should be exported. If T is an array type,
subscripting is exported if and only if the IndexType
component is exported. If T is an enumerated type, its enumerated value identifiers
are not exported unless they are mentioned explicitly in
T's with clause; subrangeType is permitted in an
exportltem to facilitate this. Only an exported type identifier may have a with
clause.
Values of the module type itself may not be
assigned or compared for equality unless := or =,
respectively, appear in the export list. Furthermore, := and = may not appear
in the export list if the module imports any variables.
The identifiers which may be exported from a module
are those which are accessible in the scope between the end of the module's
declarations and the end of the module; loosely, these are just the identifiers -declared at the outermost level
in the module.
A module is a closed scope; i.e., identifiers
declared outside the module are not known inside unless
they are known in the immediately enclosing scope, and either are pervasive or
are explicitly imported into the module (by the
imports clause in the module definition, or because
they appear in the formal parameter list of the module declaration). Importing
is discussed in detail in 7.3.
The optional identifier following module in the type definition may be used within the definition to name the entire value, i.e., for
self-referencing.
A module type may be prefixed with the symbols machine dependent, which simply means that it may contain other
machine-dependent module and record declarations, fixed addresses in variable declarations (see 7.), extended
characters of the form $ddd (see 4.), type converters
involving types with implementation-dependent representations (see 6.5), uses of StorageUnit.Address (see 6.1.2), and machine-code
procedure declarations (see 10.); a module
which is not machine-dependent may not contain any of these things. Thus it is possible to tell from the heading of a module type
whether it contains any machine
dependencies or not. Note that machine-dependent
identifiers exported from a machine-dependent
module, as well as the machine-dependent module type itself, may be used in other modules which are not machine-dependent.
Since exported types can only be
manipulated by exported routines, the routines serve to encapsulate the
machine-dependencies.
The standard representation
of a module is not defined.
moduleType ::= [ machine dependent ]
module [ identifier ]
importClause exportClause
moduleBody endModule
endModule ::= end module I end identifier
importClause ::= imports "("
importltem "," importltem } ")" I
empty
importltem ::= pervasive
bindingCondition identifier I typeConverter exportClause ::= exports exportList [";"] I empty
exportList ::=
"(" exportltem { "," exportltem} ")"
exportltem ::= bindingCondition identifier [ with
exportList ] I ":=" I "=" subrangeType
bindingCondition ::= const
I readonly I var I empty
A module may include an
initial action which is executed whenever a new variable of the module type is created, and a final action which is executed whenever such a variable
is
destroyed.
Note that if several module variables are declared, as in the program fragment
begin x:Ml; y.M2; z•Ml;
... end
the order of creation is x, y, z, and
the order of destruction is z, y,
x. This follows from the fact that the three declarations start three nested
scopes, all of which end at the end (see 7.3).
A module may also specify an invariant which is supposed to be true during the lifetime of the module variable (i.e., after the execution of the
initial action and before the execution of the
final action), except perhaps when one of the procedures of the module has been
called and has not yet returned. Like other
assertions, this one may be empty or a Boolean expression.
In the former case the content of the assertion is supplied in a comment. This comment is of course ignored by the compiler, but
presumably is interpreted by the verifier.
In the latter case the assertion must be a legal Boolean expression, but it
generates code only if the checked option is enabled for
the enclosing scope.
The abstraction function, necessary for one
approach to the verification of modules [Hoare 1972,
London et al. 1977], maps the variables inside the module into a value of the
module type. The need for this mapping in verification
arises because a variable of the module type is
represented inside the module by different variables. The body of the
abstraction function may contain
constructs outside Euclid in the same way that assertions may, i.e., within comments. The abstraction function is not callable
from a Euclid program.
moduleBody ::= checkedClause declaration [ ";" initialAction
invariant finalAction
checkedClause ::= checked
I not checked I empty
declaration ::= empty I
pervasive declarationPart { ";" pervasive declarationPart }
declarationPart ::= constantDeclaration I variableDeclaration I typeDeclaration
procedureDeclaration I functionDeclaration
initialAction initially
routineDefinition ";" I empty
invariant ::= [abstraction
functionDeclaration] invariant assertion ";" I empty
assertion ::= expression I empty
finalAction ::= finally
routineDefinition
";" I empty
The following example outlines how one might
package floating-point numbers and operations
on them in a module. Examples of complete modules may be found in section 12
and Appendix B.
var
Real: machine
dependent module
exports (Add, Subtract, Times, Div, Greater, const
zero, number, Value with
(:=, =, sign, exponent, mantissa))
type
Exp = -80#16 7F#16; type Mant = 0 OFFFFFF#16 type Value = machine
dependent record
var
sign (at
0 bits 0 .. 0): 0 .. 1 := 0 var
exponent (at
0 bits 1 .. 7): Exp := 0
var mantissa (at 0 bits 8 .. 31): Mant := 0 end Value
const
zero: Value := (0,0,0)
intine function number (m: signedInt, ex: Exp) returns
num; Value =
imports (Mara)
begin
if
m < 0 then num.sign := 0 else num.sign := 1
end if
num.mantissa
:= Abs(m); num.exponent := ex
end number
function
Add (const 1, r Value) returns sum: Value =
code ... end Add
inline function Greater (const 1, r Value) returns
Boolean =
imports
(signedInt<<=Value)
begin
{use
type converters to compare I & r as signedlnts}
return True when (signedInt<<=lia/ue(0)
> (signedlnt<<=Value (r)) return False
end Greater
•••
end Real
6.2.4
Machine-dependent records
A machine-dependent
record type is a restricted kind of record type which allows the programmer to. specify
the exact position and size of each variable field. The position is specified in StorageUnits, where
the first StorageUnit of the record is numbered 0, and then in bits, where the first bit of the
specified StorageUnit is numbered 0, and the bit numbering continues to successive StorageUnits in
the obvious way. The ordering of bits in a StorageUnit is implementation-defined. If the bits
clause is omitted, the field occupies an integral number of StorageUnits, and its size is computed
from the size of its type; the value is right-justified in the field. The compiler's
responsibility is to check that fields do not overlap and that each field is at least large
enough to hold values of its type. The size of a value of machine-dependent record type is
determined by the largest position specified by the declaration, where the value of the at clause
(in StorageUnits) is added to the ending value of the bits clause (in bits). An
implementation may place restrictions on how fields overlap natural storage
boundaries. The index type specifying bits must be a subrange of integer, and must be manifest
except possibly for the last component of the record.
A machine-dependent
record may have constant components like an ordinary record. It may not have
any parameters. All its variable components must have position specifications, and they cannot
be exported or passed as variable parameters. Furthermore, they must all have types whose
standard representation is specified. Note that the standard representation of a
machine-dependent record is specified, but the standard representation of an ordinary record is not.
An alignment clause,
aligned mod a, in a machine-dependent record declaration forces a value of the record type to be
allocated so that the machine address of its first StorageUnit is 0 mod a; a must be a power of 2.
The module in which a
machine-dependent record type appears must be a machine-dependent module.
mdRecordType
::= machine dependent record [ alignmentClause ] mdDeclarationPart ";"
mdDeclarationPart } endRecord
mdDeclarationPart ::=
constantDeclaration I
var identifier "C at manifestConstant [ bits
simpleType ")" ":" typeDefinition [ initialization
6.2.5.
Set types
A set type defines the range of
values which is the powerset of its base type. Base types must be simple
types. Operators applicable to all set types are:
union
set
difference: i appears in a-b if and only if it appears in a and
not in b. xor symmetric
difference: i appears in a xor b if and only if it appears
in
exactly one of a and
b.
intersection
in membership
<=, >= set inclusion
Sets can be built up
from values of the base type as described in section 8. The standard representation of a set S : set
of B is defined if. B is a manifest type and the standard representation of values of B is
defined. It is a sequence of n significant bits, where n=(B.last-B.first+1), preceded by
any number of insignificant zero bits. If the significant bits are numbered 0, 1, ..., n-1, then bit i is one if
and only if x is in S and B.Ord(x)=i.
setType
::= set of baseType
baseType
simpleType
There is one standard component of a set
type T: T.BaseType the
base type
Examples:
type Hue = set of Color
type SubtractivePrimaries = set
of red .. green type SymSet
= set of -5 .. +5
type
EntrieslnUse = set of Arrayl.lndexType
6.2.6.
Pointer and collection types
A variable which is declared in a program (see
7.) is referred to by its identifier. The variable exists during the entire
lifetime of the scope to which it is local, and such a variable is therefore called static. In contrast, variables may also be generated dynamically, i.e., without much correlation to the structure of the
program. These dynamic
variables are generated
by the standard procedure component New described below; since they do not occur in an explicit variable declaration, they cannot be
referred to by an identifier. Instead, they may
be referred to by a pointer value which is provided by
New when the dynamic variable is generated.
A pointer type thus consists of an unbounded set of values pointing to elements of the same type. No operations are
defined on pointers except the test for
equality, the pointer following operator t which yields the variable
referred to by the pointer, and the standard
function component, Index, which converts a pointer into an integer.
The standard representation of a pointer is the same as
the standard representation of an AddressType.
A dynamic variable must be an element of a collection. A collection is not a type: it is a variable which behaves very much like an array variable.
Just as an element of an array variable A can be referenced by subscripting A with an index whose type is the index type of A (A.lndexType), so an element of a collection C can be
referenced by subscripting C with a pointer
whose type is the pointer type of C (tC). There are two differences:
No two collections have the same pointer type.
Hence the pointer alone is sufficient to
specify the collection, and we allow pt as shorthand for C(p), where p is of type tC.
There are no operations which produce pointer
results, except the standard procedure C.New
which creates a new variable (or an explicit type conversion). Hence the storage allocation strategy for collections can
be quite different from the strategy for arrays.
The reason for having collections is that two
pointers to different collections are guaranteed to
point to different variables; two pointers to the same collection are either
equal, and point to the same variable, or unequal, and point to non-overlapping
variables. Hence collections are a means by
which the programmer can express some of his knowledge about the ways in which his program is using pointers. If he
prefers not to do this, or has no knowledge
about pointers to variables of type T which can be
expressed in this way, he can simply declare a
single collection of Ts and use it everywhere.
There are no operations on collections. A
collection may not be assigned to another collection.
In fact, there is nothing to do with a collection except to subscript it, or to
pass it as an actual parameter.
Associated with every collection is a zone which provides storage for its variables. A zone is a module variable with three special components (and
possibly other components):
a variable storageBlocks which
is a collection of a record type containing a special component (and possibly
other components):
theStorage,
a StorageUnit
a procedure Allocate(size,
alignment: unsignedlnt,
var pointer tstorageBlocks) a procedure Deallocate(pointer tstorageBlocks, size: unsignedlnt)
These components must not be exported; they are
intended only for use by the standard procedures
New and Free. A zone must be a machine-dependent module variable. Note that a collection es zone must be imported as a variable
into any scope in which C.New or C.Free
is called. If C is reference-counted, C.zone must also be imported as a
variable into any scope in which a
non-local variable of type tC is assigned to. Appendix B contains examples of module types which- implement zones.
A collection declared without a zone will get a standard
zone called SystemZone. This zone is not
pervasive (since it is a variable), but must be imported where it is needed.
A collection can be reference-counted, in which case a variable in the collection will be freed automatically when no pointers to it remain. The
optional manifest constant is an integer
which gives the maximum reference count which should be maintained; any
variable to which more than this number of pointers ever exists at one time may
never be freed. The Free procedure does not
exist for a reference-counted collection.
collectionType ::= [ counted [ manifestConstant ]
] collection of objectType [ in zone ]
objectType ::= type
zone ::= variable
pointerType ::= "t" collectionVariable
collectionVariable ::=
variable
There are six standard
components of a collection variable C:
 a pointer which points to no variable at all.
a pointer which points to no variable at all.
the
object type. If there are any unknowns in the collection definition, C.ObjectType is a parameterized type
with formal parameters
corresponding to the unknowns, in the same order (see 6.3).
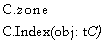 the zone (see above).
the zone (see above).
a function which takes a
pointer to C and returns an integer.
This function has only one defined property: it is one-to-one.
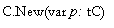 allocates a new variable v of type T in collection C and assigns
the pointer to v to
the pointer variable p. C.New
imports C as a variable. This procedure works by calling Allocate for the pointer's zone with T.size and
T.alignment as parameters. It
gets back a tstorageBlocks, and
uses the theStorage component
in this block as the first StorageUnit for the newly created variable. It is up to the verifier of the zone to ensure that a sequence of at least n free StorageUnits begins there if Allocate(n, i, p) was called, and that the storage allocated does not overlap with that of
any other variable. Any
initialization specified by the type of v is performed. If the object type of C is parameterized, and any of the actual parameters are unknown, then
specific
allocates a new variable v of type T in collection C and assigns
the pointer to v to
the pointer variable p. C.New
imports C as a variable. This procedure works by calling Allocate for the pointer's zone with T.size and
T.alignment as parameters. It
gets back a tstorageBlocks, and
uses the theStorage component
in this block as the first StorageUnit for the newly created variable. It is up to the verifier of the zone to ensure that a sequence of at least n free StorageUnits begins there if Allocate(n, i, p) was called, and that the storage allocated does not overlap with that of
any other variable. Any
initialization specified by the type of v is performed. If the object type of C is parameterized, and any of the actual parameters are unknown, then
specific
|
C.Free(var p: tC)
|
values
for these parameters must be supplied as additional parameters to New, and in the same order in
which they appear in the
type's formal parameter list, so that the variable
being created will have a definite type.
frees
the variable v pointed to by p and sets p to C.nil. The variable becomes undefined. C.Free imports C as a variable. Any finalization specified by the
type of v is performed. Then the Deallocate procedure for C's zone is called with a pointer to the storageBlocks variable from which v was originally allocated
by C.New, and the size which was given to
C.New. This procedure is not defined for reference-counted
collections.
|
Note that New and Free are procedures which
violate the strict type checking of Euclid. These
procedures, explicit type conversions (see 6.5) and machine code routines (see
.10), are the only ways of doing so.
Examples:
var myStreatns: collection
of Stream(unknown) in ioZone type StreamRef = cmyStreams
var userinput,
userOutput, anyStream: StreamRef
myStreams.New(userinput, keyboard) {create & initialize input Stream}
myStreams.New(userOutput, display) {also an
output stream}
myStreams.New(anyStream,
any)
var stringStorage: collection
of string(unknown)
type StringRef(maxLength: StringIndex) = t stringStorage(maxLength)
6.3 Parameterized types
It is possible to declare a parameterized type by
including a formal parameter list (see 10.) in the type declaration:
type T(a: signedInt, b color) =
Every reference to such a type (i.e., every use
of T except in an import or export list) must have an actual parameter list which supplies values for
all the formal parameters. Thus, a parameterized
type is like a template, from which a number of types can be obtained by supplying actual parameters for the formals. The formal
parameters of a type must be constant, and of an
assignable type; a type may not have a variable formal parameter.
When a parameterized type is referenced in the
formal parameter list of a procedure, an actual
parameter of the reference can be a previous formal parameter of the procedure
(see 10.). Thus, procedures can be written to accept
actual parameters whose type is any reference
to a parameterized type.
The built-in type constructors array of T, (subrange), case c of ... (variant
part of a record type), and tC also take parameters. In fact, the first three can take
parameters of any simple type, and the
last can take any collection. Thus all four are unlike user-defined parameterized types, in which the types of the parameters
are specified in the formal parameter list. For
subrange, array and case the actual parameters must be constants, but need not
be manifest. Thus, textually identical occurrences of one of these constructors
do not necessarily produce the same type.
The case constructor is normally used in the
declaration of a type T in which its parameter is in turn declared to be a (necessarily constant) formal
parameter of T. Note that when T is referenced, actuals
must be supplied for all its formals, even though some of the formals may be referred to only in a variant which is not
selected. Furthermore, the actual parameter
supplied for the tag must be a manifest constant, any or unknown.
Parameters of a type may be referenced like
record components; thus after type T(p: color) . . .; var .r. T(red)
the expression x.p=red is
True. Note that the parameters of a module type need not be exported, since they are declared outside the module
definition.
When a parameterized type T is referenced (e.g., in the declaration of a variable),
the actual parameters are substituted
for the formals, and an, unparameterized type results. In certain cases, however, Euclid makes it possible to defer fixing
the value of a parameter. In particular:
If a parameter is the tag of
a variant, it may be specified as any, so that a variable can be changed from
one variant to another during execution, by assigning
values of different variants to the variable.
If T is referenced as the object type of a collection, one or
more parameters may be specified as unknown, and
fixed only when a variable in that collection is created.
If T is the type of a formal parameter of a routine, one or
more parameters of T
may be specified as parameter.
This is a shorthand which indicates that they are
to be passed as additional parameters of the
routine.
The first two cases are
described in detail below; for the third, see 10.
The special value any may be used as an actual
parameter of a type reference, provided that the
corresponding formal is only used as the tag of a variant. Suppose V is such a parameterized
type, with a formal parameter s, of enumerated type
T, used as a tag (there might
be other formals, but they are omitted in this example). Then V(any) is a type
whose values are the union of the values of V(i) as i ranges over all the
elements of T. It differs from
any particular V(i)
in two important ways:
If x is declared to be
of type V(any), only those components of x which are outside the case constructor with tag s can be referenced. A discriminating case statement (see 9.2.2.2) can be used to bind x to an identifier y whose type is V(i),
and then all the components of y can be referenced in the scope of the discrimination.
The value of the parameter x.s, and hence the choice of variant, can be changed during execution by assignment to x (but not, of course, to y if y is of type V(i)). This
is the only case in which any property of a variable which is determined by the parameters of its type can be changed
after the variable has been created.
The special value unknown may be used as an
actual parameter in a type reference, provided the
reference appears as the object type of a collection. A variable in the
collection can only be created by the
standard procedure New, however (see 6.2.6), and when New is called, actual parameters must be supplied for all the unknowns in
the object type; note that any is a legitimate
actual parameter. Hence a type never involves unknown except in the object type
of a collection. When a pointer to collection of
T(..., unknown, ...) is dereferenced to yield a variable
v, that variable has type T(..., x,...), where x is the value which was
supplied to New when v was
created.
As in other cases where the parameters of types
are not manifest constants, the compiler may
have to generate legality assertions to ensure that the type of a dereferenced
pointer has some property demanded by the context in which the dereferenced
pointer is used. If the unknown parameter is only
used as the tag of a variant, a discriminating case statement can be used to bind a referenced variable to an identifier of
known type, just as is done with any.
Note that all actual parameters in an object type other
than any and unknown are evaluated when
the collection is declared, not when a variable in the
collection is created.
parameterizedTypeReference
::= [containingVariable "."] typeldentifier
typeActualParameter
{ "," typeActualParameter } ")"
typeActualParameter ::=
expression I any I unknown I parameter
Examples of type
definitions:
type FamilyMember(sex: SexType) = forward
var members-. collection of FamilyMember(unknown) type FamilyMember = record
var age: 0 .. 100
var mother, father, sibling: tmembers var oldestChild: t.members
end FamilyMember
type Subject =
FamilyMember(any) type
Family = t members
6.4 Type compatibility
This section defines the
conditions under which two types are the same, and describes the rules for type compatibility in
the language. The basic idea is this: a type identifier is an abbreviation for its definition.
After all such abbreviations have been removed, two types are the same if their definitions
look the same. However, a module type, or any type exported from a module, is
considered to be different from any other type; hence operations on such a type are restricted to procedures defined in
the module.
Two
types are the same if
their expanded definitions are equal. The expanded definition of a type is
obtained by the following algorithm:
Start
with the type.
Replace each type
identifier by its definition, unless the definition is a module type, or the identifier was
exported from a module. During this replacement, substitute any actual parameters for the
corresponding formals.
Replace x.itsType by the type of x. If x
is a formal parameter, and its type has occurrences
of parameter, replace them with additional formals as described in 10.
Repeat
these replacements until there are no more to be done. The result is the
expanded definition.
Two
expanded definitions are equal if,
when all extended parameters of
types (including array, subrange, case and t constructors) are removed, they
are identical sequences of basic symbols;
each extended parameter in one
sequence is equal to the corresponding extended parameter in the other sequence.
The extended parameters of a type
are the actual parameters, if any, together with the values of all constant identifiers used
free (i.e., not declared) in the type definition.
If the compiler cannot
determine whether or not two types are the same (e.g., because their constant parameters are not
manifest), and they must be the same for the program to be legal, then the compiler will
assume that they are the same, and generate a legality assertion guaranteeing this fact for the
verifier to prove.
When a value is assigned to a
variable, or a variable is bound to an identifier, the types must be compatible according
to the following rules:
an operand for any operator other
than dot, subscripting, and t, must have a type which is not parameterized;
in
an assignment, both types must be the same, except that
ranges of variables on
the left side may differ from the ranges of the corresponding components on the right side (Note,
however, that other
parameters of types, such as array bounds, may not differ). In a legal Euclid program, each actual value being stored
will be within
the range of the
corresponding variable. Where the compiler cannot verify the legality of an
assignment, it will generate one or more legality assertions concerning the range of the actual
value.
occurrences of any as
an actual parameter in the type of the variable, and not within the object type of a collection,
may correspond to
occurrences
of any value in the type of the right side. Thus,
a
T(red) may be assigned to a T(any), but not the reverse. Furthermore, a
pointer to T(red) may not be
assigned to a pointer to T(any).
In a binding (see
7.4), The type Tv of the variable must be the same as the type Ti
of the identifier.
If the binding is part of a procedure or function call, however, actual
parameters in the
specification of Ti may be other formal parameters of the
procedure or function (see 10).
The
following table summarizes the transitions which are possible:
|
To (formal
|
I
|
T(red)
|
T(any)
|
|
or left side)
|
1
|
|
|
|
From (actual or right side)
|
|
|
|
|
|
T(red)
|
|
|
bind assign
|
assign
|
|
T(any)
|
|
|
discriminate
|
bind assign
|
6.5
Explicit type conversions
In recognition of the
fact that controlled breaches of the type system are sometimes necessary, Euclid provides a mechanism
for specifying such breaches. It takes the form of a class of pseudo-functions called
type-converters. A type-converter specifies an explicit conversion from one
type (the source) to another (the target). The two types must have the same size, and must not be
parameterized. The function takes a value of the source type as its single argument, and produces
a value of the target type. No code is generated by the function, except perhaps for code
supplied by the implementation to bring the representations of the argument and result into the
standard form specified in this report.
It is possible to
specify procedure or function as the source type, so that a
program can get hold
of the starting address for a routine in order to link to it from a machine
code body (see 10.)
A type converter is
automatically declared in the largest scope in which both the source type and the target type are declared.
However, it may not be referenced in this scope, but must be explicitly imported into any inner
closed scope which references it.
If either source or target
type,has an implementation-dependent representation, the type converter can
only appear in a machine-dependent module.
typeConverter ::= targetType
"<<." sourceType targetType ::= typeldentifier
sourceType ::=
typeldentifier I procedure I function
Examples: (from Appendix B)
CellPtr<<=AddressType SBPir<<=CellPir
7. Declarations and
denotations of constants and variables
"Declare,
if thou host understanding."
Job 38, 4
A constant is a literal constant, or an identifier
declared as a constant, or an expression containing
only constants.
constant
::= expression
A constant declaration. consists of an
identifier denoting the new constant, followed optionally
by its type, and then by an expression which defines its value. The defining expression is evaluated, and its value becomes the value
of the constant, which can never change
thereafter. The type of the constant, if specified, must be assignable, and assignment-compatible with the type of the defining
expression (see 6.4).
A structured constant may be used to define a
constant of a structured type which is not a module
type. The constants within the parentheses are the values of the components of
the structured value. For a record, the order is the
order in which the components appear in the definition. For an array a, the order is a(a.IndexTypefirst) to a(a.IndexType.last).
If the structured type contains other structured
types as components, their values are in turn represented
as nested structured constants.
constantDeclaration ::= const idList [
":" typeDefinition 1 ":=" expression I const idList ":" typeDefinition ":="
structuredConstant
idList
::= identifier { "," identifier }
structuredConstant
::= "(" [ constantltem { "," constantltem ")"
constantltem ::= constant I
structuredConstant
A variable declaration consists of a list of
identifiers denoting the new variables, followed by
their type and optional initialization, or it consists of a binding. The initialization
is exactly equivalent to an assignment statement
executed immediately after the declaration of which
the variable declaration is a part. A bind declaration specifies that each of the identifiers in the bindList is to be bound to an already existing
variable, rather than to a newly created one
(see 7.4). If the variable binding condition is readonly, or omitted, then the newly declared identifier cannot be changed within the
new scope. In particular, it cannot be assigned
to, or passed as a variable parameter, and the same restrictions apply to
any variable which is part of it. All the
renamings of components of a single entire variable
must be accomplished within a single bindList, since otherwise the no-overlap
rule (see 7.3) will be violated.
The fixed address, if present, specifies the
physical address in memory where the variable is to
be allocated. It is the compiler's responsibility to ensure that a variable
allocated at a fixed address does not
overlap any other variable. A fixed-address component is
either a variable declared at a fixed address, or a
module type containing a fixed-address component.
Such a component may only appear as a component of a machine-dependent module type which is not the definition of a type
identifier (i.e., is not named). It is a consequence
of the no-overlap rule that only one variable of each type with a fixed-address
component may be declared.
Note that a variable may not be declared to be of type
integer, but only of some subrange type.
Constants may be of type integer, however.
variableDeclaration
::= var variableDeclarer
bind
variableBinding I bind "(" bindList ")"
bindList
::= variableBinding {"," variableBinding}
variableBinding
::= varBindingCondition identifier to variable
varBindingCondition
::= readonly I var I empty
variableDeclarer ::= idList [ fixedAddress ":"
typeDefinition [ initialization
fixedAddress ::= "(" at
manifestConstant ")"
initialization
::= ":=" expression
Examples:
const
iC, jC := -1 {iC and jC will be integers and have the
value -1} const tc: Color := red
var k,
1: -5 .. 5 := iC {both variables initially have the value of 1C} var sensitivity:
array Device of Classification
bind
var arrayEntry to a0(1) {a0(1) must be a valid reference. arrayEntry
is simply another name for a0(1) over the scope of this declaration}
bind input
to UserInput {input is Userinput for the scope of this
declaration, but cannot be changed within the scope}
var a,
b : signedlnt := iC {a and b initially have the value -1}
var cv:
Color
const
tenN := 10*n
const
huel := Hue(red, blue)
const
diskldle: Interrupt Word := (0, 1, finishedOk, nullCommand)
var diskControl
(at 104#8): Interrupt Word := diskldle
var dateTable:
array 1 .. 10-IC of Date
const index: array -1 .. 9 of
unsignedlnt := (3,1,4,1,5,9,2,6,5,3,6)
var str.
string(10)
var
shades-. array Color of Hue
var
jimH, butler, ralph, jimM, gerald: FamilyMember (male)
var Smiths, Joneses: Family var j, x,. y, z, max-. signedlnt
var
p, q: Boolean := False
var
strPl, strP2: StringRej(100) var real2, rea12:
Real.Value var p1, p2: tmembers
var
country. (NotKnown, UnitedStates, Canada, GreatBritain, Other)
var
operator (plus, minus, times) var col: Color
var
anArray. array OneToOneHundred of signedlnt
Denotations of
variables designate an entire variable, or a component of a variable, or a variable referenced by a pointer
(see 6.2.6). Variables or constants occurring in examples below are assumed to be declared as indicated above.
Associated with every variable is a main variable which is entire; the variable is said to be part of its main variable. One variable is part of another if, roughly, an assignment to either can change
the value of the other, and the space of possible values of the first variable is a (not necessarily proper) subset of the
space of possible values of the second variable.
The following sections define main variables and part precisely. "Part
of" is a transitive relation: if x is part of y and y is part of z then x is part of
z. It is also reflexive:
x is part of x. Two variables are the same if and only if each is part of the other. Two variables overlap if and
only if one is part of the other.
variable ::= entireVariable
l componentVariable
7.1. Entire variables
An entire variable is denoted by its identifier,
and is its own main variable. An entire variable
is never part of another entire variable (see 7.4). Hence, two entire variables
never overlap.
entireVariable
::= variableldentifier
variableldentifier
::= identifier
7.2. Component
variables
A component of a variable is denoted by the variable
followed by a selector specifying the component.
The form of the selector depends on the structuring type of the variable.
componentVariable
::= indexed Variable I fieldDesignator I
referencedVariable
baseVariable
::= variable
Corresponding to each kind of component
variable described below, there is a corresponding
constant expression which differs from the component variable in only one way: a constant array, record, or module appears in place
of the base variable.
7.2.1.
Indexed variables
A component of an array variable is denoted by
the variable followed by an index expression.
The main variable of an indexed variable is the main variable of the array variable. The indexed variable is part of the array
variable. An indexed variable it is part of another indexed variable i2 if and only if either they
have the same array variable and the
two indexes are equal, or the array variable of it is part of 12.
indexed
Variable ::= arrayVariable "(" expression
")"
arrayVariable
::= baseVariable
The index expression and the index type declared
in the definition of the array type must be
subranges of the same type. The value of the index expression must be a value
of the index type for the program to be legal.
Examples:
index(-1)
dateTable((i mod 10-iC) + 1) shades(green)
7.2.2.
Field designators
A component of a record or module variable, or a
formal parameter of the type of any variable,
is denoted by the variable followed by the field identifier of the component or
parameter. The field identifier of a module
component must be exported in the type definition.
A field designator is a variable only if the field identifier was declared as a
variable; otherwise it is a constant. A variable
field designator is readonly if the field identifier
was exported as readonly. If a field designator is a variable, its main
variable is the main variable of the
containing variable, and the field designator is part of the containing variable. A field designator fl is part of
another field designator f2 if and only if
either their containing variables are the same and their field identifiers are
identical, or fl's containing variable is
part of f2.
field Designator ::= containingVariable
"." field Identifier containingVariable
::= baseVariable
fieldldentifier ::=
identifier
Examples:
str.length
jimM.sex
diskIdle.command
{a manifest constant}
reall.mantissa
7.2.3.
Referenced variables
If p is a pointer
variable whose collection C is of type T, p denotes that
variable and its pointer value, whereas pt is short for C(p),
which denotes the variable of type T referenced by p. The main variable of a referenced variable is the main
variable of the collection to which the variable belongs. The referenced
variable is part of the collection variable. A referenced
variable rl is part of another referenced variable r2 if and only if either
they have the same collection and the two pointers are
equal, or the collection of H. is part of r2.
referencedVariable ::=
collectionVariable "(" pointer ")" I pointer "t" collectionVariable
::= baseVariable
pointer ::= factor
Examples:
Smithst
Smithst.mother strP1t.text(1)
7.3
Scope rules and importing
A scope is a region of text in
which an identifier (other than a field identifier) is known with a single meaning. A scope is
either
a type or routine declaration,
beginning with the type, procedure, or function and ending at the end of the
declaration, or
a region of the program
between.the end of a declaration and the next unmatched end, or
a record or module definition,
bracketed by record or module and the matching end, or
a routine
definition (see 10.)
A module or routine definition is
called a closed scope; other scopes are open. Note that these closed scopes are nested within the open
scopes of the surrounding declarations.
An identifier is accessible in a scope S if it is declared in that scope, or
accessible
in the enclosing scope if S is open, or
pervasive in some enclosing scope,
or imported into S, or a formal parameter of the type or routine declaration in which S appears, if
S is closed.
An identifier must be accessible
in S to be used in S in any context except as a field identifier.
New
identifiers are declared
as
record or module components,
as
enumerated value identifiers,
in a
declaration at the head of an executable scope, as parameters of a for or
discriminating case, or
as
formal parameters of a routine or type declaration.
These new identifiers are
accessible within the newly established scope. They are not accessible outside of this scope,
except that:
Field identifiers of
records, or of modules if exported, are accessible outside the scope in a suitable field
designator, which is considered to be a continuation of that scope.
If an enumerated type
is the definition in a declaration of type T, its
value identifiers are
declared in the same scope as T, rather than in the inner scope of
the type
declaration.
Note that the name
declared by a module type or routine declaration is not declared in the closed scope which is the definition, but in the
enclosing scope; it must be imported explicitly into that scope if the definition is
recursive. The formal parameters of the declaration, if any, are accessible in the closed scope.
Note also that in the case of a module, the type may only be used within the module
definition as the object type of a collection
(see 6.)
A new
identifier may not be introduced which is the same as any other identifier
accessible in the scope. Of course, an
identifier accessible in the enclosing scope of a closed scope, but not imported or pervasive, is not accessible, and
hence may be reused. This is the only way in which an
identifier can become inaccessible in an inner scope.
An identifier used in a scope and not declared
in that scope is said to be free in that scope. Any identifier which is free in a closed scope must
be accessible in the immediately enclosing
scope, and either explicitly imported into
the closed scope, or declared pervasive in some enclosing scope; see 6.2.3 for
syntax. An identifier declared pervasive is imported, as a constant, into all scopes nested within the one in
which it is declared; hence it may not be redeclared in any of these scopes.
Only constant identifiers may be declared pervasive, since variables cannot be imported as constants.
If a routine is imported into a scope S, every identifier which it imports must also be imported into S. If a module type is imported into S,
every identifier imported by the type which
is in turn imported by any component of the type which is exported, must also
be imported into S. Furthermore,
in both cases a variable imported var into such a module type or routine must be imported var into S, rather than readonly. Thus, it is not possible for a scope
to cause any variable to be referenced or modified which the scope could not itself have referenced or modified (except that a called
routine may be able to access components of a
module, when the caller could only access the module as a whole).
An explicitly imported identifier has the same
status as a newly declared, pile. The imports clause can specify (in the binding condition) for each
variable identifier whether it is imported as an ordinary variable, or readonly (the
default). A readonly variable may not be changed
explicitly; i.e., it may not be assigned to, or passed as a variable parameter.
A readonly variable is not a constant, however,
since its value may change as a result of statements
executed in an enclosing scope where it is not readonly. A variable identifier may not be imported as a constant. A constant identifier
is always imported as a constant; its
binding condition may be const or may be omitted.
Any identifier used in a formal parameter list is
automatically imported into the closed routine
or module body which follows. If an enumerated type is imported, all its enumerated value identifiers are automatically imported.
If a record or module type is imported, any of
its field names (if it is opaque, any exported field names) can be used as field
identifiers in a field designator whose containing variable is of that type.
A closed scope has the property that all its
possible interactions with the rest of the world can be determined
by examining its imports list, identifiers declared pervasive in some enclosing
scope, its parameters, and, in the case of a module, its exports list. In the
case of a routine no
exports list is needed, since nothing is left after the
routine returns.
The defining expressions for constants and the index
expressions for variable bindings are evaluated
when a scope is entered, or when a record or module variable or constant is declared, or when a dynamic record or module variable is
created.
Note that a pointer cannot be
dereferenced within a given scope unless its collection is accessible in that scope, and cannot be dereferenced to a
variable unless the collection is accessible
as a variable in that scope; these rules are identical to the rules for indexed
variables.
A declaration in Euclid cannot have any side
effects, with one exception: a declaration of a module
variable may have side effects from the execution of the module's
initial action, if the module imports any
variables.
7.4 Binding
An
identifier may be bound to
a variable when it appears
as a var formal parameter in a procedure declaration
(functions cannot have var parameters);
in a variable binding in a
variable declaration.
A variable to which an identifier is bound is said to be renamed.
The scope of a binding is the scope of the
declaration, and within this scope the identifier represents the variable. That is, the initial value of
the identifier is the value of the renamed
variable at the time of binding, and the last value assigned to the identifier
will be the value of the renamed variable after control
finally leaves the scope. If this variable is part
of an array, its index is evaluated when the scope is entered; if it is part of
a referenced variable, the pointer is evaluated
when the scope is entered.
The type and range of the identifier being bound
must be the same as the type and range of the
renamed variable to which it is bound (but see 10 for the use of parameter). A component of a packed structure or a machine-dependent
record must not appear as a renamed variable.
Note that this does not prevent discrimination of a packed variant record (see 9.2.2.2), since in. that case it is the entire
record which is renamed, not a component.
Any variable imported by a scope is considered
to be renamed. For open scopes, any variable
free in the scope is considered to be imported by the scope, and hence to be,
renamed. A variable is renamed even if it is
bound or imported readonly (but not if it is passed
as a constant parameter), and even if it is readonly in the outer scope.
In order to allow a simple description of the
rules for renaming variables, we will assume for the rest of this section that
a procedure does not import any variables; the initial and final actions of a module are considered to be parameterless
procedures for this purpose. Any procedure which
does import variables is to be rewritten as a procedure which accepts the imported variables as additional variable formal
parameters, and every call is rewritten to
supply the same variables as additional actual parameters. This also applies to
procedures in modules: if a component of the
module is imported as a variable by the procedure,
that component is supplied as an additional actual parameter (in spite of
the-fact that it might not be exported). The rewritten
program will behave exactly like the original one.
In order to ensure that the rewritten program is
a legal one, however, we must (and do) impose the following requirement on the
original program: any free variable in a procedure must have the property that it would be accessible as a
variable in every scope which contains a call of
the procedure, if the field identifiers required to reach it were exported as variables.
The language ensures that an entire variable can
never overlap (see 7.1) any other variable accessible in the same scope which has a different main
variable, or in other words that
the value of an entire
variable can change only
as the result of assignment
to that variable or one of its parts, or
as a result of a procedure call in which that variable was
the main variable of an actual parameter corresponding to a variable formal
parameter;
an
assignment to an entire variable can never change the value of any other
variable which is accessible in the scope containing the assignment, except one of its own parts.
To prevent binding from destroying this
non-overlap property, the following restriction is imposed: no two variables which are renamed on entry to a
scope can overlap. If the compiler cannot determine
whether or not two variables overlap (e.g., a(i) and a(j) overlap iff j), it will assume that they don't, and generate a legality
assertion to that effect for the verifier
to deal with. Note that variable identifiers which it is illegal to access in a
scope because of this rule are not therefore
inaccessible and hence are not eligible for redeclaration.
An identifier is accessible everywhere in its scope, except inside nested closed scopes which do not import it.
In general, identifiers that are declared as
constants cannot cause any aliasing problems, since
their values can always be copied. Of course the compiler is free to use a
pointer rather than copy the value if it can determine
that the meaning of the program is the same; this
will certainly be true if the variable involved does not overlap any variable
accessible in the same scope. In other
cases the value must be copied.
Copying may be very inefficient for large arrays
or records. Hence we impose a stronger rule
in this case: if a large variable v is accessible in a scope as a constant, no variable which overlaps v can be renamed on entry to the scope. The definition of
"large" is implementation-dependent. If
the programmer really wants a large array or record to be copied, he can declare a constant for that purpose; unlike
passing a constant parameter, a constant
declaration looks like an operation which makes a copy, and indeed it generally
does, unless the constant is manifest.
A parameterized type with a large actual
parameter which is a variable poses a similar problem,
since in general the value will have to be copied when such a type is used to declare an identifier, unless the variable is not modified
in the scope of the declaration. Hence
the same restriction is imposed in this situation: the compiler will reject a
program which requires copying a large value in this way.
8. Expressions
"Grant me some wild
expressions, Heavens, or I shall burst."
Farquhar, The Constant
Couple, V, iii
Expressions are constructs denoting rules of
computation for obtaining values of variables and generating new values by the
application of operators. Expressions consist of operands (i.e., variables and constants), operators, and
functions.
The rules of composition specify operator precedences according to seven classes of operators. The multiplying operators have the highest
precedence, then the adding operators, then the
relational operators, then not, then and, then or and finally, with the lowest precedence, ->. Sequences of operators of the
same precedence are executed from left to right.
Since functions cannot have side effects, the order of
evaluation of operands in an expression need not
be defined.
The rules of precedence are
reflected by the following syntax:
factor ::= variable I literalConstant I constantldentifier
I functionDesignator I set "("
expression ")" I "-" factor
set ::=
setTypeldentifier elementList ")"
elementList
::= element "," element } I all I empty
element ::= expression I
simpleType
term ::= factor I term
multiplyingOperator factor
sum ::= term I sum
addingOperator term
relation ::= sum I sum
relationalOperator sum I sum [ not ] in simpleType negation ::= relation I not relation
conjunction ::= negation I conjunction
and negation
disjunction ::= conjunction
I disjunction or conjunction
expression ::= disjunction I
disjunction "->" disjunction
Expressions in an element list for a set of type
T = set
of U must all be of type U. TO denotes
the empty set of type T, T(all) denotes the set
containing all the elements of U, and T(x..y) denotes the set of all values in the interval
x..y. If V is a subrange of U, T(V) is an abbreviation for T(V.first..V.last).
Note that the operators on sets, summarized in
6.2.5, can be used to perform bitwise logical operations,
and in fact these operators are intended to be implemented with the machine's logical operations on words.
Examples:
Factors: x
15
(x+y+z) Abs(x+y)
Hue(blue, col, green)
Hue(all)
SymSet(1, 5, -4 .. -1, 2)
-x
Terms: x*y
i div (1-i)
x mod (5*y)
Sums: x+y
huel
xor shades(red) i*j+1
huel
- Hue(blue)
Relations: x
= 15
x not= 15
p <= q
(i<j) = (j<k)
cv in huel
cv not in shades(orange) i in oneToOneHundred i not
in 25 .. (e5)
|
Negations:
Conjunctions:
Disjunctions:
|
not (p not= q) not
q
x<=y and y<z p and not q
p
or (x>y)
|
Expressions: False
-> p or (x > y)
a*a > b*b -> (Abs(a) > Abs(b))
8.1. Operators
The compiler is expected to check that no
overflow will occur during the evaluation of an expression:
if it is unable to verify this, it must put out a legality assertion for the
verifier to check (see 6.1.2).
The types of the operands must be the -same as
the types specified below, or subranges of those types. A consequence is that a
value whose type is exported from a module cannot be an operand in an expression outside the module, except
perhaps of the "=" operator.
8.1.1. Multiplying operators multiplyingOperator ::= "*"
I div
I mod
 operator operation
operator operation
* multiplication
set intersection
div division with
truncation
mod modulus
type of operands
integer
any set type T
integer
type of result
integer T
integer
The div operator truncates toward zero, so that -(a div b).-a div b. Also, a div -b.-a div b. The mod operator is defined by a mod b=a-((a div b)*b). The right operand of div or mod must be non-zero.
8.1.2.
Adding operators addingOperator
::= "+" I "-" I xor
operator operation
addition set union
subtraction
set difference
xor symmetric
difference
type of operands
integer
any set type T
integer
any set type T
any set type T
type
of result
integer T
integer
T
T
When used as an operator
with one integer operand only, - denotes sign inversion.
8.1.3.
Relational operators
relationalOperator "="
I not "=" I "<" I "<=" I ">" I
">=" I in I not in
operator type of operands result
= not= most types Boolean
< > any enumerated or subrange type Boolean
<= >= any enumerated, subrange or set type
in any enumerated or subrange type Boolean
not in and its set type, respectively
any enumerated or subrange type and an index type (not value), respectively.
Notice that all enumerated
types define ordered sets of values.
The operators <=and >= stand for less than
or equal, and greater than or equal respectively. They may also be used for comparing values of set type,
and then denote set inclusion. If p and
q
are Boolean expressions, p=q denotes their equivalence.
8.1.4 Other operators
|
operator
|
operation
|
type of operands
|
type of result
|
|
not
|
logical negation
|
Boolean
|
Boolean
|
|
and
|
logical "and"
|
Boolean
|
Boolean
|
|
Or
|
logical "or"
|
Boolean
|
Boolean
|
|
->
|
logical implication
|
Boolean
|
Boolean
|
The right operand of and need not be legal if
the left operand is False; the right operand of or need not be legal if the left
operand is True; the right operand of -> need not be legal if the left operand is False.
8.2. Function designators
A function designator specifies the evaluation of
a function. It consists of the identifier or field
designator designating the function, and a list of actual parameters. The
parameters are expressions, and their
values are substituted for the corresponding formal parameters (see 9.1.2, 10, and 11).
function Designator ::= function [ "C
expression { "," expression typeConverter
"(" expression ")"
function
::= [ containingVariable "." ] functionldentifier
f unctionIdentifier ::=
identifier
Examples:
FindMax(Index)
Gcd(147, k)
Power(Index(i), str.length)
Real.Add(reall,
ReaLnumber(314159,1))
9.
Statements
"The statements was interesting,
but tough."
Huckleberry
Finn, Ch. 17
Statements
denote algorithmic actions, and are said to be executable. statement ::= simpleStatement I
structuredStatement
9.1. Simple statements
A simple statement is a statement of which no part
constitutes another statement. The empty
statement consists of no symbols and denotes no action.
simpleStatement ::= assignmentStatement I
procedureStatement I escapeStatemetit I assertStatement
1 emptyStatement
emptyStatement ::= empty
9.1.1.
Assignment statements
The assignment statement serves to replace the current
value of a variable by a new value specified as an expression.
assignmentStatement ::= variable ":="
expression
Note that assignment is not allowed if the type T of the variable is not assignable, or if
the variable is readonly. A type is not assignable if
it is a collection type, or if it is an exported type
for which assignment was not exported, or if it is a structured type which has
a variable component whose type is not assignable.
Examples:
x := y+z
p := i in 1..99
p := (1<=i) and (i<100)
shades(blue) := Hue(blue,
Color.Succ(c))
reall := real2
9.1.2.
Procedure statements
A procedure statement serves to execute the
procedure denoted by the procedure identifier. The
procedure statement may contain a list of actual parameters which are assigned or bound
to the corresponding formal parameters declared in the
procedure declaration (cf.
10). The correspondence is established by the positions
of the parameters in the lists of actual and formal parameters, respectively.
There are two kinds of parameters: constant parameters
and variable parameters; routine and type parameters are not permitted.
In the case of a constant parameter, the actual parameter must be an expression (of
which a
variable is a simple case). The
corresponding formal parameter represents a local constant
of the called procedure, and the current value of
the expression is the value of this constant.
As in the case of a constant declaration, the type of the actual parameter must
be assignable, and assignment-compatible with the
type of the formal (see 6.4). Note that a constant
formal parameter is not a manifest constant, since its value is not known at compile-time.
In the case of a variable parameter, the actual parameter must be a variable, and the corresponding formal parameter is bound to this actual
variable (see 7.4) during the entire execution
of the procedure. The types must be the same. A variable parameter must be used whenever the parameter represents a result of the
procedure.
procedureStatement ::=
procedure [ "(" expression { "," expression } ")"
procedure ::=
[containingVariable "."] procedureldentifier
procedureldentifier identifier
Examples:
TreeSort(DA)
ZeroArray(DA) Replace(str, i, 3,
9.1.3
Escape statements
An escape statement serves to
indicate that further processing should continue at the
statement following the smallest enclosing
repetitive statement (exit), or that control should
return immediately from the routine currently
being executed (return). Note that any module
variables which are destroyed as a result of the escape will have their final
actions executed first. The when clause, if present,
makes execution of the escape conditional. Thus,
the statement
S when B
is equivalent to
if B then S end if.
An expression must not appear in a return
statement unless the statement is in a function body, and in that case the type
of the expression must be assignment-compatible with the type of the function's result value.
escapeStatement escapeBody [ when expression ]
escapeBody ::= exit return j return
expression
Example:
begin
var flag : (a, b, finished) :=
finished for
... loop
flag
:= a, exit flag := b; exit
|
end loop
case
flag of
a => ... end
b => ... end finished => end case
end
|
a
b
... end finished
|
9.1.4
Assert statements
An assert statement
introduces an assertion (see 6.2.3) which is supposed to hold whenever control reaches that point in the program.
The compiler treats it as a comment, as it does with the assertions supplied by invariant,--pre and
post clauses, unless the assertion is a Boolean expression, and the checked option is
specified for an enclosing block, in which case the Boolean expression is evaluated, and execution of
the program is terminated if it is False.
assertStatement
::= assert assertion Examples:
assert x<y and y<z assert {e(w**0 = x**y}
9.2.
Structured statements
Structured statements are
constructs composed of other statements which have to be executed either in sequence (compound
statement and block), conditionally (conditional statements), or repeatedly (repetitive
statements).
structuredStatement ::=
compoundStatement I block
conditionaiStatement
I repetitiveStatement
9.2.1.
Compound statements and blocks
The compound statement
specifies that its component statements are to be executed in the same sequence as they are written.
Note that a compound statement is a statement, and has no brackets; hence a
sequence of statements can be written wherever a single statement can be written.
compoundStatement ::= statement { ";" statement
} Example:
z := x x := y; y := z
A block is a compound statement within which new identifiers
can be introduced. The symbols begin and end act
as brackets to delimit the scope of the new identifiers. If a scope S starts with checked, each legality assertion in S, and each assertion in the source text of S which is a Boolean expression, is compiled into a runtime
check, which aborts execution of the
program if the assertion is False. If S starts with not
checked, any occurrence of checked in an
enclosing scope is ineffective in S.
block
::= begin executableScope end
executableScope ::= checkedClaUse [ declaration ";"
] statement
Example:
begin
const twoX := 2*x var signedint
w := twoX*twoX-x
begin
bind
y to
w,
y :=
twoX*twoX*twoX+y { really means w twortwortwoX+w}
end
end
9.2.2.
Conditional statements
A conditional
statement selects for execution a single one of its component statements. conditionalStatement ::= ifStatement I
caseStatement
9.2.2.1.
If statements
The if statement specifies that a statement is to
be executed only if a certain condition (Boolean
expression) is True. If it is False, then either no statement is to be
executed, or the statement following the
symbol else is to be executed.
The statement
if a then b elseif ... end if
is an abbreviation for
if a then b else if ... end if end if.
ifStatement ::= if expression
then executableScope elseifClause
[ else executableScope ] end if
elseifClause elseif
expression then executableScope }
The expression between the
symbols if or elseif and then must be of type Boolean. Examples:
if x<15
then z := x+y, cv := blue else
cv := red; z := 0
end if
if pl not members.nil then p1 .:= plt.relations; p2 := members.nil end if
if str.text(1) = $$$ then country := UnitedStates elseif str.text(1) = $# then country := GreatBritain else country := NotKnown
end if
9.2.2.2.
Case statements
The case statement
consists of an expression (the selector) and a list of elements, each labelled by a set of manifest
constants of the type of the selector. It specifies that the one element is to be executed whose
label contains the current value of the selector. A special label otherwise can be used to
label a statement which should be executed if none of the other labels contains the current
value of the selector. If none of the labels contains the selector, and there is no otherwise, the program is
illegal. Each element, except the otherwise element, must be terminated with end followed
by one of the constants in its label.
If the selector is discriminating
an object, the parameter bound to the object is automatically declared in each case list
element, either as a constant whose value is the expression in the object, or as a variable bound to
the variable in the object. The expression or variable in the object must be a variant
record, say of type T(any) or T(unknown), and the tag of this record, specified by the on clause, is used to select one of the case list elements; in this situation, each case label list
of the discriminating case statement must correspond to exactly one variant of the record. Within
the element selected by a particular value of the tag, say red, the parameter has the type T(red). Thus with the type declaration
type T(tag: (red,
gren, ...)) = record
case tag of
red. => .
green =>
. . .
end case
end T
the program
var anyx: T(any); ...;
with x := anyx case tag of red =>
green =>
end
case
is equivalent to
var anyx: T(any); ...;
case anyx.tag of
red => const x T(red) := anyx; green => const .r. T(green) := anyx,
end case
except that the constant
declarations in the latter would not be legal, because it is illegal to assign a T(any) to a T(red).
caseStatement
::= simpleCase I discriminatingCase
simpleCase
::= case expression of caseBody end case
discriminatingCase ::= with object case identifier of
caseBody end case caseBody ::= caseListElement ";" caseListElement }
otherwiseElement ";"
caseListElement ::= caseLabelList
".>" executableScope end caseLabel I empty
otherwiseElement ";"
otherwise ".>" executableScope I empty
object
::= const ] parameter ":="
expression I
varBindingCondition
parameter bound to variable
parameter
::= identifier
|
Examples:
case
|
operator of
plus =>
minus =>
times =>
end case
|
x
:= x+y end plus
x := x-y end minus
x
:= x*y end times
|
case i of
1 => cv := red end 1
2 => cv := blue end 2
3,8 => cv := green end
3
4..6,9,10 => cv := yellow end 4 otherwise => cv := purple end case
with s bound to anyStreamt case dev of {begin
new line}
display => s.height :=
s.height +1 end
display
tape, disk =>
s.position :=
s.position +1 s.buffer(s.position) := $N end tape
keyboard => end keyboard {don't send characters to input
device}
otherwise => {also null)
end case
9.2.3.
Repetitive statements
Repetitive statements
specify that certain statements are to be executed repeatedly. If a bound on the number of repetitions
is known before the repetitions are started, or if the repetition is controlled by a
generator, the for statement is the appropriate construct; otherwise the loop statement should be used.
A repetitive statement introduces a new scope. The
declarations of this scope take effect before the repetition starts, and remain in effect until
the end of the repetition. The statements
of the scope are executed repeatedly.
repetitiveStatement
::= loopStatement forStatement
9.2.3.1.
Loop statements
The statements in the scope are executed repeatedly until
control leaves the scope through an escape
statement.
loopStatement ::= loop
executableScope end loop
Examples:
loop; exit when Color.Ord(tc) =
.x; tc := Color.Succ(tc) end
loop
loop
if Odd(i) then z := zsx end
if
:= i div 2
exit when 1=0
x := x*x end loop
loop k := i mod j; i := j; j := k; exit when j = 0; end loop
9.2.3.2.
For statements
The for statement indicates that a statement is
to be repeatedly executed while a progression of
values is assigned to a new constant identifier called the parameter or controlled constant of the for
statement.
forStatement ::= for
parameter generator [ ";" ] loop executableScope end loop generator
::= in moduleType I [ decreasing ] in indexType I in
setExpression setExpression ::= expression
The parameter is declared as a constant in the
scope. The type of the parameter is the type of
the value component of the module type, the type of the elements of the index
type, or the base type of the set.
A module type generator is a module type which
has three components with special names: variables
called value and stop, and a procedure called Next. These names must be exported.
A for statement of the form
for v in
moduleTypeGenerator loop LoopBody end loop is equivalent to the block
begin var crec: moduleTypeGenerator, loop exit when crec.stop
begin
const v:=crec.value; LoopBody
end crec.Next
end
loop
end
The initial and final actions in the declaration
of the generator module type can perform any
initialization or cleanup which may be appropriate; note that the final action
is executed whenever control finally leaves the for
statement, whether normally or via an escape
statement.
A for statement with an
index type generator, of the form
for v in AnIndexType loop LoopBody end loop
is equivalent to the block
begin var vv:AnIndexType := AnIndexTypefirst
if vv <=
AnlndexType.last
then
loop
const
r=vv
LoopBody
exit when
vv=AnlndexType.last
vv:=AnlndexType.Succ(vv)
end loop end if
end
If decreasing is present,
interchange first and last, and replace Succ by Pred and <= by >= . A for statement with a set expression generator, of
the form
for v in SetExp loop LoopBody end loop
is equivalent to the
statement
begin
const se:=SetExp for v in
SetExp.BaseType
loop
if v in se then LoopBody end if end loop
end
Note that if the generator imports
no variables, the loop body and the generator are independent, and interact
only through the parameter values which are passed from the generator to the body. Thus termination can be proved
solely as a property of the generator.
Examples:
for Im in OneToOneHundred
loop if anArray(10>max then max := anArray(lm) end if end
loop for ci decreasing in Color loop Q(ci) end loop
|
9.2.4 Other uses of binding
If a record variable is to be used a number of
times in field designators, it convenient
to bind a short identifier to it (see 7.4). Note that the binding is fixed
to the scope. Example:
begin
bind d to dateTable(i+5);
if d.month = 12 then d.month := 1; d.year
:= d.year+1 else d.month := d.month+1
end if
|
is often on entry
|
is
equivalent to
if dateTable(i+5).month = 12 then dateTable(i+5).month := 1
dateTable(i+5).year := dateTable(i+5).year+1 else dateTable(i+5).month := dateTable(i+5).month+1 end if
and,
also equivalent to
begin
bind
d to dateTable (i+5)
bind
(m to d.month, y to d.year)
if m = 12 then m := 1; y := y+1 else m := m+1 end if
end
10. Procedure declarations
"But
a name for an effect."
Cowper
A procedure declaration serves to define a part
of a program, and to associate an identifier with
it so that it can be activated by procedure statements; a function declaration
(see 11.) plays a similar role. Collectively, procedures
and functions are called routines.
A machine-code routine is exactly like an
ordinary routine, except that its body is a sequence
of machine instructions, represented as manifest integer constants according to
an implementation-dependent convention. An
implementation may define a more elaborate syntax
for code bodies. Machine code routines may only appear in machine-dependent modules.
procedureDeclaration
::= procedureHeading "=" routi neDefi n ition routineDefinition ::= importsClause preAssertion
postAssertion routineBody routineBody ::= begin executableScope end identifier I forward I codeBlock codeBlock ::= code manifestConstant ";"
manifestConstant } end identifier
The procedure heading specifies
the identifier naming the procedure, and the formal parameter identifiers (if any). The parameters are either
constant or variable parameters (see
also 9.1.2).
The standard representation of a routine
identifier must be defined by the implementation, so that a routine can be the
argument of an explicit type conversion. A linkage between a machine code routine and a Euclid routine R can then be done by making a declaration of the
form
var Blink :
routineLink (at
100) := routineLink<<=procedure(R)
and writing in the machine code body an appropriate jump
to the routine address stored at 100. The type routineLink would of course have to be properly, declared in the
program.
If the heading is prefixed by inline, this is a
hint to the compiler that the procedure body should
be copied at each call. Such copying tends to result in faster execution, at
the expense of a larger object program. The meaning
of the program is not changed by the inline
prefix. However, an inline routine may not have a forward body or import its
own name (i.e., may not be recursive).
procedureHeading ::= [
inline ] procedure identifier formalParameterList formalParameterList ::= formalSection
{ "," formalSection } ")" I empty
formalSection ::= pervasive
bindingCondition identifier { "," identifier }
":" typeDefinition
preAssertion
::= pre assertion ";" I empty
postAssertion
::= post assertion
";" I empty
A formal section without const, var, or readoniy implies that its constituents are
constants.
A type specification for a formal parameter may have
actual parameters which are other formal
parameters; thus
procedure f(n: 0..1000, a: array 1..n of
signedInt)
is a legal declaration. This
procedure might be called as follows: begin
var aa: array 1..200 of
signedInt; f(200, aa); ... end
Furthermore, in order to reduce the proliferation
of parameters which would otherwise be required,
we make the following rule: the type of a formal parameter may be a parameterized type with some or all of the actual
parameters of the type replaced by the symbol parameter. Each actual parameter
of the type for which parameter appears is treated as though it appeared as an additional formal parameter
of the procedure, and the appropriate actual
parameter of the procedure is supplied in every call. Thus
type Ta(rr. unsignedlnt)=array 1..n of signedInt; procedure f(a: Ta(parameter))
is also legal and is equivalent to the previous
declaration of f, except that all the calls on f will
be modified appropriately. The previous call would be written
f(aa)
and would be modified to
become
f(200, aa)
The use of the procedure identifier in a procedure statement
within its declaration implies recursive execution of the procedure.
Examples of procedure
declarations:
type DataArray(n: 1..256) = array 1..n of signedInt;
procedure TreeSort(var a: DataArray(parameter)) =
{This procedure is a version of Floyd's TreeSort algorithm
in CACM, 7 (1964), p. 701. TreeSort sorts
the array a in ascending order} post
{(a in Perm(a') and j in 1 .. a.n-1) -> a(j) <= a(j+1)}
begin type Index
= a.lndexType
inline procedure Swap(11, 12: Index) =
imports (var a)
post {a
in Perm(a')
and a(i1)=a'(i2)
and a(12)=a'(11)1
begin
const t := a(il)
a(iI) := a(i2); a(i2) :=
end Swap;
procedure
SiftUp(low, high: Index) =
imports(var a)
pre tj in 2*(low+1) .. high -> a(j) <= a(j div 2)}
post {j in 2*low
.. high -> (a(j) <= a(j div 2)
and a in
Perm(a'))} begin var son-. Index := low
loop const father
:= son
son := 2*father
return when son
> high
if son<high
and a(son)<a(son+1)
then son := son+1 end
if return when a(son)
<= a(father)
Swap(son, father)
assert fj in 2*low
.. son -> a(j) <= a(j div
2)}
end loop
end
SiftUp

 i
decreasing in 1 .. (Index.last d iv 2) loop
i
decreasing in 1 .. (Index.last d iv 2) loop
SiftUp(i, Index.last)
assert {Sifted(2*i,
/ndex.last)} end loop
i decreasing in 1 ..
Index.last-1
loop
Swap(1, 1+1)
SiftUp(1, i)
end
loop
end
TreeSort
type DataArraySegment(m, n: 1..256) = array m..n of
signed Int
procedure
ZeroArray(var a: DataArraySegment(parameter,
parameter)) = post {i iu a.m a.n
-> a(i)=0}
begin
for i in ai ndexType
loop a(i) := 0 end loop
end ZeroArray
procedure Replace(var target: string(parameter),
first,
len: Stringlndex, source. string(parameter)) = pre (target.length+source.length-len
<= target.maxLength) post
t (i in 1..first-1 ->
target.text(i) = targee.text(0) and
(i in first
.. first+source.length-1 ->
targetteA4(0=source.text(i-first+1))
and
(i in first+source.length target.length+source.length-len
->
target.text(i) =
target'aext(i+len-source.length)) and
(target.length
= target'.length + source.length-len)} begin
const offset := source.length-len
bind (var tgt to target.txt, var ti
to target.length) if offset
> 0 then
for i decreasing in first+len tl loop
Igt(i+offset) := tgt(i) end loop
elseif offset < 0 then
for i in first+len tl
loop tgt(i+offset) :=
tgt(i) end loop
end if
tl := tl+offset
for i in 1 .. source.length loop tgt(first+i-1) := source.text(i) end
loop
end. Replace
procedure Append(var
target string(parameter), source: string(parameter)) = pre (targetlength+source.length
<= target.maxLength)
post {(target.length
= target'.length + source.length) and
( i in 1..targel.length -> target.text(i) =
targer.text(i)) and
(t in
1 source.length -> target.text(i+target'.length)) ='source.text(i))}
begin
for i in 1 source.length
loop
target.text(i+target.length) :=
source.text(i)
end loop
target.length := target.length +
source.length
end Append
11. Function declarations
"The
Form remains, the Function never dies."
Wordsworth
Function declarations serve to define parts of
the program which compute a value. A function is activated by the evaluation of
a function designator (cf. 8.2) which is a constituent of an
expression.
functionDeclaration
::= functionHeading "=" routineDefinition
The function heading specifies the identifier naming the
function, the formal parameters of the
function, and the type of the function.
functionHeading ::= [ inline
] function identifier
formalParameterList
returns resultName typeDefinition
resultName ::= identifier
":" I empty
Functions may return values of any assignable
type (see 9.1.1). If the result name is supplied,
then within the function declaration there must be one or more assignment statements assigning a value to the result name, and the
value of the result name when the function
returns determines the value of the function. If no result name is supplied,
the result must be supplied in every return
statement. A return statement without any value is supplied automatically just before the end of the body. A
machine-code function returns its value
by an implementation-defined convention.
Occurrence of the function identifier in a function
designator within its declaration implies recursive
execution of the function.
A function may not have variable parameters, or
import anything var (although importing a variable
readonly is legal); hence, a function cannot have side effects, but must return
the same value whenever it is called with the same
actual parameters.
Examples:
function FindMax(a: DataArraySegment(parameter, parameter))
returns index: signedInt =
post {k in
a.m a.n
-> a(index) >= a(k)}
begin
index
:= a.m
for i in a.m+1 a.n
loop
assert {k in a.m i-1 -> a(index) >= a(k)}
if a(i) > a(index) then index := i end
if
end
loop
end
FindMax
function Gcd(m, tr.
signedInt) returns
signedlnt =
imports(Gcd)
begin if n=0 then
return m else return Gcd(n, m mod
n) end
if end Gcd
function Power(x:
signedint, yc unsignedint) returns
z: signedlnt =
begin var w: signedlnt; var 1: unsignedlnt
w := x; :=
y; z := 1
loop
assert {z*(w**0 = x**y}
exit when i = 0
if
Odd(i) then z := z*w end if
i := i div 2
w
:= w*w
end
loop assert {z = x**y} end Power
function Substr(s:
string(parameter), first. Stringlndex, len: StringLength)
returns r string(len) =
pre first+len
<= s.length+1
post {(i in 1..len
-> r.text(i) = s.text(i+first-1)) and r.length = len} begin
r.length := len
for i in 1..len loop r.text(i)
:= s.text(i+first-1) end loop end
Substr
function Catenate(sl:
string(parameter), s2: string(parameter),
size StringLength) returns
r string(size) =
pre sl.length
+ s2.length <= size
post {(r.length
= sl.length + s2.length) and
(i in
1..s1.1ength -> r.text(i) =
sl.text(i)) and
(i in 1..s2.1ength -> r.text(i+sl.length) =
s2.text(0)}
begin
r.length := sl.length + sl.length
for
i in
1 .. sl.length
loop r.text(i)
:= sl.text(i) end loop
for i in 1 .. s2.length
loop r.text(i+sliength)
:= sl.text(i) end loop end Catenate
12. Programs
"All are but parts of one stupendous whole."
Pope, An Essay
on Man
A Euclid program consists of a sequence of module
type declarations, possibly prefixed by an
include clause which causes additional text to be inserted into the program.
The include clause is a list of items,
each of which names a file containing the text of a Euclid program; the file is named by a literal string,
according to an implementation-defined convention. If from is present, only the named module types are included;
otherwise all the declarations in the
file are included. If the same type identifier from the same file is included
more than once, duplicates are suppressed. If different
files contain types with the same name, however,
an error results because of the normal Euclid rule which forbids redeclaration
of names.
An implementation may use some method other than
the textual substitution described above
to provide this facility. In particular, it may take advantage of the fact that
an included file has already been compiled. Thus
the structure of compilation units is intended to
facilitate separate compilation (although not to require it).
The report does not specify how the module types declared
in programs are instantiated to start a program.
program ::= cornpilatiOnUnit
compilationUnit
::= [ includeClause ";" ] typeDeclaration ";"
typeDeclaration }
includeClause ::= include
includeltern { ";" includeltern }
includeltem
::= [ id { "," id from ] fileName
fileName ::= literalString
Example:
type NumberTable = module exports(Search, Delete, Insert)
{This module implements a table of numbers, e.g.,
currently open accounts, as an associative memory}
pervasive const tableSize := 763
pervasive type Table" nd ex = 1 .. tableSize
pervasive type CyclicScan(item: signed!nt) = {a
generator for a for loop} module exports (Next, value, stop)
const start :=
(item mod tableSize)+1
var value: Tablelndex := start
var stop: Boolean := False
procedure Next.=
imports(var value,
start, var stop)
begin
if value = tableSize then value
:=
else value := value+t end if
stop := ( value not= start)
end Next
end CyclicScan
type State =
(fresh, full, deleted)
type TableEntry(flag.
State) =
record
case
flag of
full => var key. signedlnt
end full otherwise
=>
end
case
end TableEntry
var table: array
Tablelndex of TableEntry(any) function
Search(key.
signedInt) returns Boolean =
imports(table)
begin
for
i in
CyclicScan(key)
loop
with
entry := table(i) case
flag of
fresh => return
False end fresh
full =>
return
True when entry.key = key,
end
full;
otherwise
=>
end
case;
end
loop;
return
False; end Search;
procedure Delete(key:
signedInt) =
imports(var
table)
begin
coast deletedEntry:
TableEntry(deleted):= (); for i in
CyclicS'can(key)
loop
with
entry := table(i) case
flag of•
full =>
if entry.key
= key then table(i)
:= deletedEntry; return
end
if
end
full
fresh => return end fresh
otherwise
=>
end Case
end loop
end
Delete
procedure Insert(key:
signedint) =
imports(var
table, Search)
begin
return when Search(key)
{if already
there};
for
i in .CyclicScan(key)
loop
case tab!
e(i).11 ag of
loop
case table(i).flag
of
fresh,
deleted =>
var TableEntry(full)
t.key := key table(i):= t end fresh
otherwise =>
end case
end loop
assert
False
{table will never be full} end Insert
const freshEntry.
TableEntry(fresh):= 0
initially
begin
for
i in tab/e.IndexType loop table(i) := freshEntry end
loop end
end NumberTable
13. A standard for
implementation and program interchange
"'That's not a regular rule: You invented
it just now.'
'It's the
oldest rule in the book,' said the King.
'Then it ought to be Number One,'
said Alice."
Alice in Wonderland, Ch.
12
One motivation for the development of Euclid was
the need for a powerful and flexible language
that could be reasonably efficiently implemented on most computers. Its
features are defined without reference to any particular
machine in order to facilitate the interchange
of programs. To establish a reasonable minimum standard for Euclid implementations, the following requirements are imposed
on every implementation.
1. Word symbols, such as begin, end, etc.,
may be written as a sequence of letters (without
surrounding escape characters). They may not be used as identifiers. An implementation may also allow such symbols to be
written in other ways (e.g. in boldface),
provided there is a straightforward transformation into the representation as a sequence of letters.
2. Blanks, ends of lines, and comments are defined as separators. An arbitrary number
of separators may occur between any two consecutive Euclid symbols, with the following restriction: no separators may occur
within identifiers, numbers, and word symbols.
3. At least one separator must occur between any pair of
consecutive identifiers, numbers, or word symbols.
4. The implementation may set limits on the size and
complexity of the source program. However, these
limits must be chosen from the following list, and must not be more restrictive than indicated below. An
implementation should not reject a program for
exceeding some limit not on this list; it may accept programs which exceed any of these limits.
a)
The range of unsignedlnt
(must include 0..216-1). The range of
signedlnt (must include -215+1..215-1).
It is recommended, but not required, that
larger subranges of integer than these be permitted, say up to 0..232-1 and -231+1..231-1.
b)
The
maximum number of elements in the base type of a set (at least 16).
c)
Depth
of nesting of scopes (at least 31).
d) Depth of nesting of parentheses in an expression (at
least 7). Number of basic symbols in an
expression (at least 50).
e) The total number of identifiers accessible in a scope (at
least 200). The total number of identifiers in the program (at least 1000).
f) The number of non-compound statements and declaration
parts in the source program (at least
2000).
g)
The
maximum number of characters in an identifier (at least 50).
h)
The
value of stringMaxLength (at least 255).
13.1 Representation of special symbols
The preferred representations of special symbols which are
not words, in the IBM PL/1 60-character set, and in the Model 33 Teletype set,
are as follows:
Special
symbol PL/1 Teletype
{ (1` (*
*)
t t
break
Programs can be converted from one representation
to another by a finite-state algorithm which
recognizes each special symbol and identifier in the source representation, and
outputs the corresponding symbol in the target
representation. During this conversion, break
characters can be supplied arbitrarily. The recommended strategy for break
characters is as follows:
If neither representation has lower case, or both do,
break characters should be preserved.
If only the source has lower case, a break character
should be- inserted between a lower case letter
and a following upper case letter in an identifier.
If only the target has lower
case, all letters should be converted to lower case, except that when a letter follows a break character, the break
character should be dropped and the letter left
in upper case.
13.2 Standard format
for programs
It is strongly recommended that an implementation include
an option to produce a version of the source
program in a standard format. The recommended standard is:
One level of indentation for each unmatched
begin, record, module, loop, if, or
case. The bracket and its corresponding end should also be indented, except in
the case of if ..
elseif .. else, and case. The for clause should not be indented. Indentation should be omitted if the entire compound statement or
declaration will fit on one line. Thus
a := 3; al := 31; a2 := 32
begin
b := 4 end
c := 5
if
b=4 then
a := 6
else
a := 7
end
if
if b=4 then a 6
else a := 7 end if
loop
end
loop
foriin0..5
loop
end
loop
A second level of
indentation for the scope in each case element. Thus
case
a of
3 =>
OutputLine(a, b, 100) InputLine(a, b, 100) end 3
4 =>
OutputLine(a, b, 200) InputLine(a, b, 200)
end 4
end
case
If a statement is too long for one line, it should be
continued on subsequent lines with a
small amount of indentation (one or two spaces).
Several short statements may
be put on the same line.
Semicolons should be omitted at the ends of lines, if they
are supplied automatically by the compiler,
as they nearly always are (see 3.1).
13.3 Annotation
It is strongly recommended that an
implementation include an option to produce an annotated
listing of the source program, in which all identifiers automatically imported
into a closed scope and the formal parameter
declarations corresponding to uses of parameter are noted.
14. Implementation notes
"'The horror of
that moment,' The King went on, 'I shall never, never forget!' 'You will, though,' the Queen
said, 'if you don't make a memorandum of it.'"
Through the Looking-Glass, Ch. 1
This section discusses
implementation techniques for parts of the Euclid language which are relatively new or tricky. Of course, no implementation is
required to use these techniques.
14.1 Identifiers
Identifiers may vary in capitalization, and in
the presence or absence of break characters. The
Euclid rule is that each time an identifier is used, it must be written the
same way it was declared (see 3.). This
rule can be efficiently enforced by normally looking up the identifier exactly as it is written, and making the more
expensive comparison which ignores break characters
and capitalization only when adding an identifier to the symbol table. If a
hash table is used, the hashing algorithm should probably be chosen to map
equivalent identifiers into the same
hash code.
An alternative implementation is to store the identifier
in a standard case, with break characters removed,
and to append to it the additional information needed to keep track of the case of each letter, and the presence of break
characters.
14.2 Parsing
Euclid has been designed to be amenable to LALR
parsing [Aho and Johnson 74]. The syntax presented in the body of the report is not LALR,
since it was chosen primarily to aid the
reader and facilitate the exposition, but a LALR grammar which generates the
same language can be obtained from the System Development
Corporation (see Preface).
14.3 One-pass translation
Euclid has been designed to permit one-pass
translation. To this end, identifiers must be declared before they are used.
Recursive routines and types may break this rule by using forward
for the definition, but all the type information must
still be present before use.
14.4 Routine parameters
Constant parameters can be passed either by
copying the value, or by reference, i.e., by passing
the address of a variable containing the value, unless the variable overlaps
some variable accessible in the routine, in which
case the parameter must be passed by copying. The
same test can be used to detect this overlap which is required to detect the
overlap of two variables; it depends
on the definition of overlap given in section 7. Note that imported variables must be treated exactly like variable
parameters for this test.
Variable parameters can be passed either by
passing the address of the variable, or by copying
the value on entry to the routine, and copying it back on exit; the latter
copying is unnecessary if it is
readonly. The absence of overlap means that this double copying will always work. If a variable is passed by double copying,
then a constant parameter whose
value is an overlapping variable can safely be passed by
reference; this might be desirable if the
constant is much larger than the variable.
14.5 Routines in modules
If a routine R is declared in a module M, and R imports
a non-manifest component c of M, then R must obtain access to c when it is called. The call
must take the form m.R(...), where m
is a variable or constant of type M. This
may be done in two ways:
By passing m (presumably by reference), and treating m as a record within c
would then be accessed by its known position
relative to the address of m.
By passing c explicitly. This might be preferable if it is the
only such component.
If R imports only manifest constants, everything can be done at
compile-time. If it imports any
non-manifest component c, however, c must in general be passed as a parameter, since it could
be different for different module variables. There is one exception: if R imports
only constants which depend only on constants
declared in module types for which only one variable
is ever created, then the references to these constants can be compiled into R, and they need not be passed as parameters.
14.6 Constant components of records and modules
The same observations apply in general to
constant components. Except under the
conditions described above, a constant component
or parameter must be stored in each
variable, since it may be different from one
variable to another. Of course, if the component
or parameter is never referenced, except during initialization, then it need
not be stored.
14.7 Finalization
If a scope declares a module
variable which includes a finalization statement, then code must be executed whenever the scope is exited which performs
the finalization. This might be done inline, or
by calling a routine. The same is true whenever a Free procedure is executed to free such a variable.
Since this machinery must be present anyway, it
can be used to allow variables declared in the scope, whose size is not
manifest, to be allocated someplace other than in the frame of the routine containing the scope. The finalization code
for the scope would then be expanded to include
code for freeing the storage used by such variables. Whether this technique is worthwhile depends on the allocation
strategy used for frames.
14.8 Inline code
In general, it is highly desirable for an
implementation to consider the use of inline code for all short routine bodies,
even if the program has not explicitly declared them inline. It is quite common for such bodies to be shorter than their
calling sequences, especially since they
can be subjected to normal optimization once they have been inserted inline.
14.9 Reference counts
There is an important special
case in which it is possible to avoid incrementing and decrementing reference counts. Suppose that the program
has a declaration type C = counted collection of ...
We
say that a scope S is C-conservative if it contains
no assignments to variables of type tC which
are not local to S,
and if furthermore any routines which S calls are also C-conservative.
Within S it is not necessary to update reference counts for
variables in C, since no variable in C can
be freed in S, and every such variable will have the same reference count on exit from S that it had on entry to S. This
idea can be extended to routines
which make assignments to variable parameters of type tC.
14.10 Representation of pointers
It is possible to take
advantage of the fact that pointers are strictly segregated by collection, to make the representation of a pointer depend on the
collection it is in For instance, a pointer
could be relative to some base address. Of course, such a representation cannot
be used in a sensitive context.
14.11 Parameterized types
Suppose
T is a parameterized type. With two exceptions, it is not
necessary to store the parameters of a variable of
type T with the variable. These exceptions (see 6.3) are
T has an actual parameter any;
the variable
is in a collection whose object type contains unknown.
In all other cases, the values of the parameters are known
from the declaration. If the declaration
contains parameter, it
must be in a formal parameter list, and the value can be passed as an additional formal (see 10.). If the type is
exported from a module, it may import components
of the module, in which case the remarks of 14.5 are applicable.
These considerations are especially relevant for variant
records and arrays. A variant record is
normally used in one of three ways:
a) To express the uniformity of several different record
structures, even though the particular
structure in use is always manifest from the declarations.
b) When the variant is expected to change during execution. A
variable of this kind must be declared with any, and the tag must be stored in
the record. Furthermore, enough space must be
allocated for the largest of the possible variants.
c) When the variable is dynamic, and the variant
is fixed at the time the variable is created. A collection of such variables
must be declared with unknown, and the tag must
be stored with each variable, or with each pointer.
The third case, involving unknown, is also appropriate
for arrays. For example, there might be a
collection of strings of widely varying length, all of which should be treated
uniformly.
When one of the bounds of an array is a
parameter, the size of the resulting type is not known
at compile-time; such a type is called length-unresolved. If
more than one length-unresolved variable
is declared in a record or routine, it is not possible to determine
the position of every such variable at
compile-time. This situation can be dealt with by constructing pointers to all the length-unresolved
components except the first one at the time
the record variable or routine instance is created, and referring to them
indirectly through these pointers.
References
Aho, A.V. and Johnson, S.C.,
"LR parsing," Computing Surveys 6, 2 (June 1974).
Ambler, A. et al., "Gypsy: A language for
specification and implementation of verifiable programs,"
University of Texas, Austin, Texas, to appear (1976).
Clark, B.L. and Ham, F.J.B., "The Project
SUE System Language Reference Manual," University
of Toronto, Computer Systems Research Group Technical Report CSRG-42 (September 1974).
Clark, B.L. and Horning, J.J., "Reflections on a
language designed to write an operating system,"
SIGPLAN Notices 8, 9 (September 1973).
Geschke, C.M. and Mitchell,
J.G., "On the problem of uniform references to data structures," IEEE Trans. SE-1, 2 (June 1975).
Hoare, C.A.R., "Proof of correctness of data
representations," Acta Informatica 1, 271-281 (1972).
Hoare, C.A.R., "Hints on programming language
design," Stanford University, Computer Science
Department, Technical Report STAN-CS-73-403 (December 1973).
Ichbiah, J. D. et al., The System Implementation Language LIS, CII, 68 route de Versailles, 78430 Louveciennes, France (December 1974).
Jensen, K. and Wirth, N., Pascal User Manual and Report, 2nd edition, Springer-Verlag; 1975.
Liskov, B. and Zilles, S., "Programming with
abstract data types," SIGPLAN Notices 9, 4 (April 1974).
Liskov, B. "An introduction to CLU," Computation
Structures Group Memo 136, MIT (February 1976).
London, R.L. et al., "Proof rules for the programming language
Euclid," to appear (1977).
Richards, M., "BCPL: A tool for compiler writing and
structured programming," AFIPS Conf.
Proc 34 (1969 SJCC).
Thompson, D.H., "Base + Builder language
definition," Technical Note 4, Computer Systems Research Group, University of Toronto (March 1976).
Wirth, N., "The
programming language Pascal," Acta Informatica 1 (1971).
Wirth, N., Modula: A language for modular multiprogramming, Institut fur Informatik, ETH,
CH 8092 Zurich (March 1976).
Wulf, W., London, R. L. and Shaw, M., "Abstraction
and verification in Alphard", New Directions in Algorithmic Languages-1975, Stephen A. Schuman, ed., IRIA (1976).
Appendix A. Collected
syntax
The syntax of Euclid, as presented in
this report, is collected below for convenient reference. The numbers in the left margin are the numbers of the sections
in which the following text appears.
3.
letter::_ "A" I "B" I
"C" I "D" I "E" I "F" I "G" I "H" I
"I" I "J" I "K" I "L" I "M" I
"N" "0" "P" "Q" I "R" I "S" I
"T" I "U" I "V" I "W" I "X" I
"Y" I "Z" I" "a I ,.b,. "c'' "d" I "e" I „f'' "g" I "h" I "i" I "j" I
"k" I "I" I "m" I "n"I "o,. "p" I "q"
I "r" I "s" I "t" I "u" I "v" I
"w"I "x" I ,'y''
octalDigit ::= "0" "1" I "2" I
"3" I "4" I "5" I "6" I "7"
digit ::= octalDigit
I "8" I "9"
hexDigit ::= digit I
"A" I "B" I "C" I "D" I "E" I
"F"
breakChar ::= <some
implementation-dependent character not a letter or digit>
|
specialSymbol
::=
|
|
|
|
|
"+" I„#„ "=” I "<" ">" "<="
|
">="
|
,._>,.
|
"(" I ")" I
|
|
"{"I "}" I ":=" I "." I "," I ";" I ":" I"
|
" I "t"
|
"=>"
|
"<<=" I "$" I "#"
I
|
wordSymbol
wordSymbol ::=
abstraction I aligned I all I and I any I array I
assert I at I begin I bind I bits I bound I case I checked I code I collection I const I
counted 1-decreasing I dependent I discriminating I div kelse I elseif I end I exit I exports I finally I for I forward I
from I
function I if I imports I in I include I initially I inline I invariant I loop
I machine I mod I module I not I of I on I or I otherwise I packed I parameter
I pervasive I post I pre I procedure I readonly I record
I return I returns I set I then I
to I
type I unknown I var I when I with I xor
4.
identifier ::= letter { letterOrDigit }
letterOrDigit ::= letter
I digit I breakChar
unsignedNumber
::= digit
{ digit } I
octalDigit octalDigit
} "#8" I
digit { hexDigit } "#16"
literalString ::=
" ' " extendedCharacter } " '
extendedCharacter
::= character
I "$" extension
extension ::= digit
digit digit I "S" I "T" I "N" I "$" I
"
literalChar ::= "$"
extendedCharacter
5.
literalConstant ::= unsignedNumber I literalString I
literalChar I enumeratedValueld
manifestConstant
::= literalConstant I
manifestConstantExpression
manifestConstantExpression ::= expression
type ::= simpleType I
structuredType I pointerType I parameterizedTypeReference
typeDeclaration ::= type
typeldentifier formalParameterList
= preAssertion typeDefinition
typeldentifier
::= identifier
typeDefinition ::= type I forward
 simpleType ::= enumeratedType I standardSimpleType I subrangeType I derivedSimpleType
simpleType ::= enumeratedType I standardSimpleType I subrangeType I derivedSimpleType
derivedSimpleType ::= [containingVariable "."] simpleTypeIdentifier
simpleTypeldentifier ::= identifier
enumeratedType
::= enumeratedValueld { ","
enumeratedValueld ")"
enumeratedValueld ::=
identifier
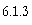 subrangeType
::= constantSum ".." constantSum constantSum
::= sum
subrangeType
::= constantSum ".." constantSum constantSum
::= sum
structuredType ::= [ packed
] unpackedStructuredType I
derivedStructuredType
unpackedStructuredType
::= arrayType I recordType I moduleType I
mdRecordType I setType I collectionType
derivedStructuredType ::= [containingVariable
"."] structuredTypeldentifier structuredTypeldentifier
::= identifier
 arrayType ::= array indexType of componentType
arrayType ::= array indexType of componentType
indexType ::= simpleType
componentType
::= type
recordType ::= record
fieldList endRecord
endRecord
::= end
record I end identifier
fieldList
::= [
recordDeclaration [";"] ] [ variantPart ] [ ";" ]
record
Declaration ::= pervasive recordDeclarationPart
"," pervasive recordDeclarationPart } recordDeclarationPart ::= constantDeclaration I
variableDeclaration pervasive ::= pervasive I empty
.
variantPart ::= case tag of variant It,"
";" variant } [ otherwiseVariant ] [ ] end case
variant
::= caseLabelList "=>" fieldList end caseLabel I empty
caseLabelList ::= caseLabel ","
caseLabel
caseLabel ::=
manifestConstant I subrangeType tag ::= constant
otherwiseVariant ::=
otherwise ".>" fieldList
 moduleType
::= [
machine dependent ] module [ identifier ]
moduleType
::= [
machine dependent ] module [ identifier ]
importClause exportClause moduleBody endModule
endModule ::= end module
I end identifier
importClause
::= imports "(" importltem "," importitem }
")"
importltem ::= pervasive
bindingCondition identifier I typeConverter
exportClause
::= exports exportList [";"] I empty
exportList
::= exportltem { "," exportltem} ")"
exportltem ::= bindingCondition identifier [ with exportList
] I ":=" I "rz." I
subrangeType
bindingCondition ::= const I
readonly I var I empty
moduleBody ::= checkedClause
declaration [ ";" ] initialAction invariant finalAction checkedClause ::= checked I not checked I empty
declaration ::= empty I
pervasive declarationPart { ";" pervasive declarationPart }
declarationPart
::= constantDeclaration I variableDeclaration I typeDeclaration I
procedureDeclaration I
functionDeclaration
initialAction
::= initially routineDefinition ";" J empty
invariant
::= [abstraction functionDeclaration] invariant assertion ";" I empty
assertion ::= expression I
empty
finalAction ::= finally routineDefinition
";" I empty
mdRecordType ::= machine dependent record [ alignmentClause ] mdDeclarationPart ";"
mdDeclarationPart } endRecord
mdDeclarationPart ::= constantDeclaration
var identifier "(" at manifestConstant [bits
simpleType] ")" ":"
typeDefinition [ initialization ]
alignmentClause ::= aligned
mod manifestConstant
 setType ::= set of baseType
setType ::= set of baseType
baseType ::= simpleType
collectionType ::= [ counted [
manifestConstant ] ] collection of
objectType [ in zone ]
objectType type
zone ::= variable
pointerType
::= "t"
collectionVariable
collectionVariable ::=
variable
parameterizedTypeReference ::=
[containingVariable "."] typeldentifier
typeActualParameter
{ "," typeActualParameter } ")"
typeActualParameter ::=
expression I any I unknown I parameter
6.5
typeConverter targetType
"<<=" sourceType
targetType ::=
typeldentifier
sourceType ::= typeldentifier I procedure I function
7.
constant
::= expression
constantDeclaration ::= const idList [
":" typeDefinition ] ":=" expression
const idList ":" typeDefinition ":="
structuredConstant idList
::= identifier {
"," identifier }
structuredConstant
::= [constantltem ","
constantltem }] ")"
constantltem ::= constant I
structuredConstant
variableDeclaration ::= var
variableDeclarer
bind variableBinding I bind "(" bindList ")" bindList ::= variableBinding {","
variableBinding}
variableBinding
::= varBindingCondition identifier
to variable
varBindingCondition
::= readonly I var I empty
variableDeclarer ::= idList
[ fixedAddress ] ":" typeDefinition [ initialization ]
fixedAddress "("
at manifestConstant
")"
initialization
::= ":=" expression
variable ::= entireVariable
I componentVariable
7.1
entireVariable
::= variableldentifier
variableldentifier ::= identifier
7.2
componentVariable
::= indexedVariable I fieldDesignator referenced Variable
baseVariable
::= variable
7.2.1
indexedVariable
::= arrayVariable "(" expression ")"
arrayVariable ::= baseVariable
7.2.2
fieldDesignator ::=
containingVariable "." fieldldentifier containingVariable baseVariable
fieldldentifier ::= identifier
 referenced Variable ::= collectionVariable "("
pointer ")" I pointer "t" collectionVariable
::= baseVariable
referenced Variable ::= collectionVariable "("
pointer ")" I pointer "t" collectionVariable
::= baseVariable
pointer ::= factor
8.
factor ::= variable I literalConstant I
constantIdentifier I functionDesignator I set I
"(" expression ")" I "-"
factor
set ::=
setTypeldentifier elementList ")"
elementList ::= element {
"," element } I all I empty
element ::= expression I
simpleType
term ::= factor I term
multiplyingOperator factor
sum ::= term I sum
addingOperator term
relation
::= sum I sum relationalOperator sum I sum not ] in indexType
negation ::= relation I not relation
conjunction ::= negation I conjunction and negation
disjunction ::= conjunction
I disjunction or conjunction
expression ::= disjunction,
I disjunction "->" disjunction
 multiplyingOperator ::= "*" I div I mod
multiplyingOperator ::= "*" I div I mod
addingOperator ::=
"+" I "-" 1 xor
relationalOperator
::= "=" I not "=" 1 "<" I
"<=" I ">" I ">=" I in I not in
functionDesignator ::=
function [ "C expression { "," expression
typeConverter "C expression ")" function ::= [containingVariable functionldentifier
functionldentifier ::=
identifier
 statement ::= simpleStatement 1 structuredStatement
statement ::= simpleStatement 1 structuredStatement
9.1.1
assignmentStatement
::= variable ":=" expression
 procedureStatement ::= procedure [ "("
expression { "," expression ")" ]
procedureStatement ::= procedure [ "("
expression { "," expression ")" ]
procedure ::= [containingVariable "."]
procedureldentifier
procedureldentifier ::=
identifier
9.1.3
escapeStatement ::= escapeBody
[ when expression ] escapeBody ::= exit 1 return I return expression
 assertStatement ::= assert assertion
assertStatement ::= assert assertion
9.2
structuredStatement
::= compoundStatement 1 block
conditionalStatement I repetitiveStatement
 compoundStatement ::= statement { ";" statement
}
compoundStatement ::= statement { ";" statement
}
block
::= begin
executableScope end
executableScope
::= checkedClause [ declaration ";" ] statement
conditionalStatement ::=
ifStatement 1 caseStatement
ifStatement ::= if
expression then executableScope elseifClause
[ else executableScope
] end if
elseifClause ::= { elseif
expression then executableScope }
caseStatement ::= simpleCase
1 discriminatingCase
simpleCase ::= case
expression of caseBody end case
discriminatingCase ::= with
object case identifier of caseBody end case caseBody ::= caseListElement { ";" caseListElement }
otherwiseElement [ ; caseListElement
::= caseLabelList "=>" executableScope end
caseLabel 1 empty otherwiseElement ::= ";" otherwise
".>" executableScope 1 empty
object ::= [ const ] parameter ":=" expression
I
varBindingCondition
parameter bound to variable parameter
::= identifier
 repetitiveStatement ::= loopStatement 1 forStatement
repetitiveStatement ::= loopStatement 1 forStatement
loopStatement
::= loop executableScope end loop
forStatement ::= for
parameter generator [
";" ] loop executableScope end loop
generator ::= in moduleType
[ decreasing ] in indexType I in setExpression setExpression
::= expression
 procedureDeclaration ::= procedureHeading "="
routineDefinition routineDefinition
::= importsClause preAssertion postAssertion routineBody routineBody ::= begin scope end
identifier I forward I
codeBlock
procedureDeclaration ::= procedureHeading "="
routineDefinition routineDefinition
::= importsClause preAssertion postAssertion routineBody routineBody ::= begin scope end
identifier I forward I
codeBlock
codeBlock
::= code manifestConstant ";" manifestConstant } end
identifier
procedureHeading ::= [ inline
] procedure identifier
formalParameterList
formalParameterList
::= formalSection ","
formalSection } ")" 1 empty
formalSection ::= pervasive
bindingCondition identifier { "," identifier }
":" typeDefinition
preAssertion
::= pre assertion ";" I empty
postAssertion ::= post assertion
";" 1 empty
f
unctionDeclaration ::= functionHeading "=" routineDefinition
functionHeading ::= [ inline ] function identifier formalParameterList
returns resultName typeDefinition
resultName ::= identifier
":" 1 empty
 program ::= compilationUnit
program ::= compilationUnit
compilationUnit ::=
[includeClause ";"] typeDeclaration {";" typeDeclaration} includeClause ::= include
includeltem {";"
includeltem}
includeltem ::= [id
{"," id} from] fileName
fileName ::= literalString
Appendix B. Zone Example
The following type implements zones for
allocating fixed-size cells from a free storage list. It makes critical use of unchecked type
conversions, of the built-in type, AddressType, of StorageUnit.Address, and of machine-dependent
records.
type ListZone(pervasive
neells, cellSize, cellAlignment: unsignedlnt) = machine dependent module exports(tifreeCen.․)
{this module
provides a zone for allocating and deal locating list cells of size cellSize}
{definition
needed by the compiler to process this module as a zone} type AllocUnit =machine dependent record
aligned mod cellAlignment var theStorage
(at 0): StorageUnit
var theRest (at 1): array 1..cellSize-1
of StorageUnit end AllocUnit
var storageBlocks: collection of
AllocUnit type SIThr
tstoragelllocks
type FreeCell = forward
var cellCollection: collection
of FreeCell type CellPtr = 1'c:el/Collection
type FreeCell
machine dependent record aligned mod cellAlignment
var link (at 0): CellPtr
var theRest (at CellPtr.size.):
array !..cellSize-CellPii%si'ze of
StorageUnit
end FreeCell
var frecti.0-lead: CellPtr var nfreeCelh,-: 0..nCells :=
procedure Allocatc(s, a: uns(griedInt,
var p: 513Ptr)
imports (var nErecCells, SBPtr<<=CellPtr,
storageBlocks,
var frecListilead, cellCollection)
pre s=cellSize and a=cellAlignment;
post nrreeCells in 0..nCells-1
begin
if nfrecCells = 0 then
p storageBiocks.nil
return
end if
nEreeCells nEreeCells-1
p := SllPtr<<=CellPir(freeListIlead) freelisalead := freelistfleadtlink end Allocate
procedure Dcalloeate(p: SBPir, s: unsignedint)
=
iffiports olrecCelks.,
CellPtr,Cull Ptr<<.SBPtr,
frecl,ist var cellCollection, storageBlocks)
pre s cc//Size
and
nirecCells and p stora,:,,eBlocks.nil
post frcel.isiHead not= ccflGoilectic/Lnil and nrrecCells 1..nCells
mar cp: CellPtr := (C'ellPtr<<=SBPIr(n))
:= freel.isaleud
:= cp
nfrecCclls := nfrea.'ells+1
end peallocate
var space: machine dependent record aligned mod cellAlignment var block (at 0): ,array 0..nCells*cellSize-1
of StorageUnit
end space
initially {set up the free list}
imports(space, CelThr, CellPtr<<=AddressType,
var freeListHead, var
cellCollection)
post freeListHead
not cellCollection.nil begin
function MakeCellPtr(i: space.blockindexType)
returns
CellPtr = imports(Cet/Ptr<<=AddressType) pre cellSize
>. CellPtr.size begin
const a: AddressType StorageUnitAddress(space.b/ock)
return (CellPtr<<=AddressType(a+i*cellSize))
end
MakeCellPtr
var
ci: CellPtr := AlakeCellPtr(0)
freeListHead := ci {pointer to first FreeCeil}
for
i in 0..nCells-2
loop const cNext := MakeCellPtr(i+1)
cit.link := cNext
ci := cNext
end loop
cit.link := cellCollection.nil {mark the end of the free list}
end
invariant nFreeCells in O..nCells
finally {all cells should be free}
imports (nFreeCells,
FreeListHead, cellCollection)
pre
nEreeCellS.nCells and freeListHead not= cellCollection.nil
begin
end
end ListZone

![]()
![]()
![]()
![]()
![]()



